This EduRev document offers 15 Multiple Choice Questions (MCQs) from the topic Binary Logic (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the following information and answer the question that follows.
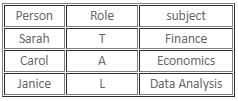
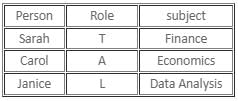
Sarah, Carol, and Janice are management students. Each failed in a different subject among Finance, Economics, and Data Analysis. Among these three students, one student always lies, the other one always speaks the truth, and the third student alternates between speaking the truth and lying, in any order. When asked about the respective subjects they failed in, each of them made the following statements:
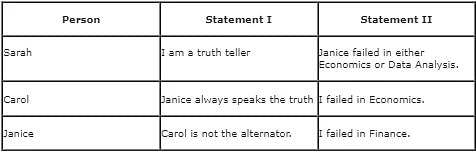
The one who is the alternator, failed in which of the following subjects?
Explanation
Let us look at the first statement of Carol - "Janice is the truth-teller". This statement implies that Carol is not the truth-teller as there is only one truth-teller, and if Janice is the truth-teller, then Carol cannot be the truth-teller. Thus, Carol can be the alternator or the liar.
Let us see the first statement of Janice - "Carol is not the alternator". If Janice is truth-teller, then Carol will be a liar, in which case Janice cannot be the truth-teller.
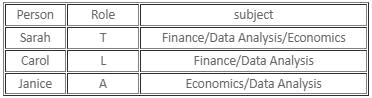
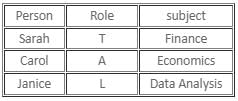
Let assume that Sarah is the truth-teller. Now, Janice can either be the liar or the alternator.
Case (i)
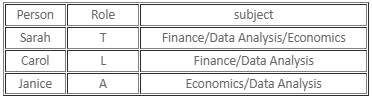
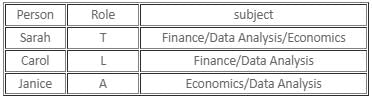
If Janice is the alternator, her first statement would be true and second statement would be false, and both the statements of Carol would be false. Hence, it is a possible case.
Case (ii)
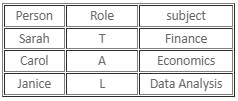
If Janice is a liar, both her statements would be false, and the first statement of Carol would be false and her second statement would be true. As there are no contradictions, this is also a possible case. In this case, Carol would have failed in Economics, Sarah would have failed in Finance, and Janice would have failed in Data Analysis.
Case (i)
Case (ii)
Hence, it cannot be determined.
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the following information and answer the question that follows.
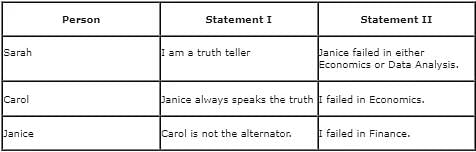
Sarah, Carol, and Janice are management students. Each failed in a different subject among Finance, Economics, and Data Analysis. Among these three students, one student always lies, the other one always speaks the truth, and the third student alternates between speaking the truth and lying, in any order. When asked about the respective subjects they failed in, each of them made the following statements:
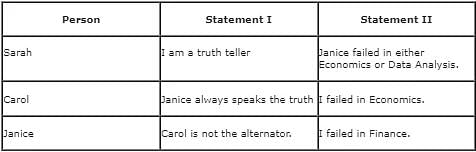
Who among the following failed in Finance?
Explanation
Let us look at the first statement of Carol - "Janice is the truth-teller". This statement implies that Carol is not the truth-teller as there is only one truth-teller, and if Janice is the truth-teller, then Carol cannot be the truth-teller. Thus, Carol can be the alternator or the liar.
Let us see the first statement of Janice - "Carol is not the alternator". If Janice is truth-teller, then Carol will be a liar, in which case Janice cannot be the truth-teller.
Let assume that Sarah is the truth-teller. Now, Janice can either be the liar or the alternator.
Case (i)
If Janice is the alternator, her first statement would be true and second statement would be false, and both the statements of Carol would be false. Hence, it is a possible case.
Case (ii)
If Janice is a liar, both her statements would be false, and the first statement of Carol would be false and her second statement would be true. As there are no contradictions, this is also a possible case. In this case, Carol would have failed in Economics, Sarah would have failed in Finance, and Janice would have failed in Data Analysis.
Case (i)

Case (ii)
Hence, it cannot be determined.
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the following information and answer the question that follows.
Sarah, Carol, and Janice are management students. Each failed in a different subject among Finance, Economics, and Data Analysis. Among these three students, one student always lies, the other one always speaks the truth, and the third student alternates between speaking the truth and lying, in any order. When asked about the respective subjects they failed in, each of them made the following statements:
Who among the three always tells the truth?
Explanation
Let us look at the first statement of Carol - "Janice is the truth-teller". This statement implies that Carol is not the truth-teller as there is only one truth-teller, and if Janice is the truth-teller, then Carol cannot be the truth-teller. Thus, Carol can be the alternator or the liar.
Let us see the first statement of Janice - "Carol is not the alternator". If Janice is truth-teller, then Carol will be a liar, in which case Janice cannot be the truth-teller.
Let assume that Sarah is the truth-teller. Now, Janice can either be the liar or the alternator.
Case (i)
If Janice is the alternator, her first statement would be true and second statement would be false, and both the statements of Carol would be false. Hence, it is a possible case.
Case (ii)
If Janice is a liar, both her statements would be false, and the first statement of Carol would be false and her second statement would be true. As there are no contradictions, this is also a possible case. In this case, Carol would have failed in Economics, Sarah would have failed in Finance, and Janice would have failed in Data Analysis.
Case (i)
Case (ii)
Hence, Sarah always tells the truth.
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the following information and answer the question that follows.
Sarah, Carol, and Janice are management students. Each failed in a different subject among Finance, Economics, and Data Analysis. Among these three students, one student always lies, the other one always speaks the truth, and the third student alternates between speaking the truth and lying, in any order. When asked about the respective subjects they failed in, each of them made the following statements:
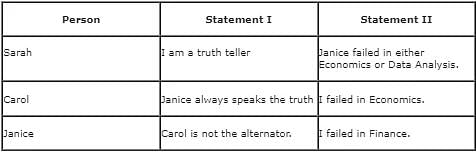
Which of the following statements must be false?
Explanation
Let us look at the first statement of Carol - "Janice is the truth-teller". This statement implies that Carol is not the truth-teller as there is only one truth-teller, and if Janice is the truth-teller, then Carol cannot be the truth-teller. Thus, Carol can be the alternator or the liar.
Let us see the first statement of Janice - "Carol is not the alternator". If Janice is truth-teller, then Carol will be a liar, in which case Janice cannot be the truth-teller.
Let assume that Sarah is the truth-teller. Now, Janice can either be the liar or the alternator.
Case (i)
If Janice is the alternator, her first statement would be true and second statement would be false, and both the statements of Carol would be false. Hence, it is a possible case.
Case (ii)
If Janice is a liar, both her statements would be false, and the first statement of Carol would be false and her second statement would be true. As there are no contradictions, this is also a possible case. In this case, Carol would have failed in Economics, Sarah would have failed in Finance, and Janice would have failed in Data Analysis.
Case (i)
Case (ii)
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the following information and answer the question that follows.
Each of three brothers, Duncan, Keith, and Norman, from Germany, are travelling to exactly one of the three countries – Sweden, Romania, and Austria, with no two of them travelling to the same country. Also, it is known that any of them can be a truth-teller, a liar or an alternator. On being asked by their parents about where they are travelling, they gave the following replies :–
Duncan:
Statement-I: Norman is an alternator.
Statement-II: Keith is not travelling to Romania.
Statement-III: I am travelling to Sweden.
Norman:
Statement-I: I am not an alternator.
Statement-II: I am travelling to Romania.
Statement-III: Keith is not travelling to Austria or Romania.
Keith:
Statement-I: I am not travelling to Sweden or Romania.
Statement-II: Duncan is a liar.
Statement-III: Norman is travelling to Sweden.
Who among the following is travelling to Austria?
Explanation
Norman's first statement is either a true statement of a truth-teller or a false statement of an alternator, irrespective of which Norman's first and third statement have to be true. This gives us the following result -
Duncan is going to Austria.
Keith is going to Sweden.
Norman is going to Romania.
Based on above, we can determine that Duncan's third statement is false and the second one is true. As the three of them have to be one of the three, i.e. truth-teller/liar/alternator, we can conclude that Duncan is an alternator and his first statement is hence, false (which means Norman is not an alternator). This leads us to the conclusion that Norman is a truth-teller; thus Norman's second statement can also be marked as true.
Hereafter, when we analyse Keith's statements, we realise they all are false. So, Keith must be a liar.
The following table tells us about the country they are travelling to:
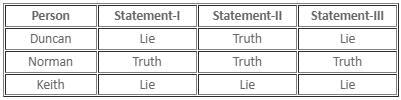
Duncan or the alternator is travelling to Austria.
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the following information and answer the question that follows.
Each of three brothers, Duncan, Keith, and Norman, from Germany, are travelling to exactly one of the three countries – Sweden, Romania, and Austria, with no two of them travelling to the same country. Also, it is known that any of them can be a truth-teller, a liar or an alternator. On being asked by their parents about where they are travelling, they gave the following replies :–
Duncan:
Statement-I: Norman is an alternator.
Statement-II: Keith is not travelling to Romania.
Statement-III: I am travelling to Sweden.
Norman:
Statement-I: I am not an alternator.
Statement-II: I am travelling to Romania.
Statement-III: Keith is not travelling to Austria or Romania.
Keith:
Statement-I: I am not travelling to Sweden or Romania.
Statement-II: Duncan is a liar.
Statement-III: Norman is travelling to Sweden.
Who among the following is a truth-teller?
Explanation
Norman's first statement is either a true statement of a truth-teller or a false statement of an alternator, irrespective of which Norman's first and third statement have to be true. This gives us the following result -
Duncan is going to Austria.
Keith is going to Sweden.
Norman is going to Romania.
Based on above, we can determine that Duncan's third statement is false and the second one is true. As the three of them have to be one of the three, i.e. truth-teller/liar/alternator, we can conclude that Duncan is an alternator and his first statement is hence, false (which means Norman is not an alternator). This leads us to the conclusion that Norman is a truth-teller; thus Norman's second statement can also be marked as true.
Hereafter, when we analyse Keith's statements, we realise they all are false. So, Keith must be a liar.
The following table tells us about the country they are travelling to:
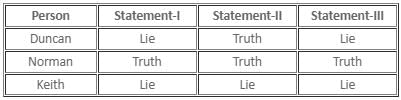
Hence, Norman is a truth-teller.
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the following information and answer the question that follows.
Each of three brothers, Duncan, Keith, and Norman, from Germany, are travelling to exactly one of the three countries – Sweden, Romania, and Austria, with no two of them travelling to the same country. Also, it is known that any of them can be a truth-teller, a liar or an alternator. On being asked by their parents about where they are travelling, they gave the following replies :–
Duncan:
Statement-I: Norman is an alternator.
Statement-II: Keith is not travelling to Romania.
Statement-III: I am travelling to Sweden.
Norman:
Statement-I: I am not an alternator.
Statement-II: I am travelling to Romania.
Statement-III: Keith is not travelling to Austria or Romania.
Keith:
Statement-I: I am not travelling to Sweden or Romania.
Statement-II: Duncan is a liar.
Statement-III: Norman is travelling to Sweden.
Who among the following is a liar?
Explanation
Norman's first statement is either a true statement of a truth-teller or a false statement of an alternator, irrespective of which Norman's first and third statement have to be true. This gives us the following result -
Duncan is going to Austria.
Keith is going to Sweden.
Norman is going to Romania.
Based on above, we can determine that Duncan's third statement is false and the second one is true. As the three of them have to be one of the three, i.e. truth-teller/liar/alternator, we can conclude that Duncan is an alternator and his first statement is hence, false (which means Norman is not an alternator). This leads us to the conclusion that Norman is a truth-teller; thus Norman's second statement can also be marked as true.
Hereafter, when we analyse Keith's statements, we realise they all are false. So, Keith must be a liar.
The following table tells us about the country they are travelling to:
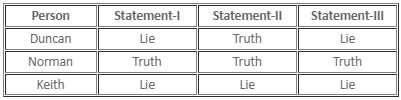
Hence, Keith, who is going to Sweden, is a liar.
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the following information and answer the question that follows.
Each of three brothers, Duncan, Keith, and Norman, from Germany, are travelling to exactly one of the three countries – Sweden, Romania, and Austria, with no two of them travelling to the same country. Also, it is known that any of them can be a truth-teller, a liar or an alternator. On being asked by their parents about where they are travelling, they gave the following replies :–
Duncan:
Statement-I: Norman is an alternator.
Statement-II: Keith is not travelling to Romania.
Statement-III: I am travelling to Sweden.
Norman:
Statement-I: I am not an alternator.
Statement-II: I am travelling to Romania.
Statement-III: Keith is not travelling to Austria or Romania.
Keith:
Statement-I: I am not travelling to Sweden or Romania.
Statement-II: Duncan is a liar.
Statement-III: Norman is travelling to Sweden.
Which of the following statements is/are false?
Explanation
Norman's first statement is either a true statement of a truth-teller or a false statement of an alternator, irrespective of which Norman's first and third statement have to be true. This gives us the following result -
Duncan is going to Austria.
Keith is going to Sweden.
Norman is going to Romania.
Based on above, we can determine that Duncan's third statement is false and the second one is true. As the three of them have to be one of the three, i.e. truth-teller/liar/alternator, we can conclude that Duncan is an alternator and his first statement is hence, false (which means Norman is not an alternator). This leads us to the conclusion that Norman is a truth-teller; thus Norman's second statement can also be marked as true.
Hereafter, when we analyse Keith's statements, we realise they all are false. So, Keith must be a liar.
The following table tells us about the country they are travelling to:
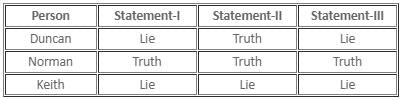
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the following information and answer the question that follows.
There are four buses, Bus-1, Bus-2, Bus-3, and Bus-4, standing at a bus stop. Each of the bus is going to exactly one city amongst City-A, City-B, City-C, and City-D. No bus is going to two cities. There are two boards on each bus which tell us about where the bus is going. It is known that there is at least one bus among them, on which both the boards are giving correct information, and at least one bus on which both the boards are giving false information. There is at least one bus on which at least one board is giving true information and the other board is giving false information, in any order.
One of the commuters read all the boards on the 4 buses and noted down the information as shown in the given table.
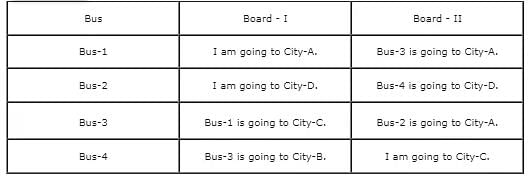
Further, on enquiry by the commuter, someone told him that Bus-4 is going to City-D, and a definite arrangement can be obtained from the information written on each bus.
Which among the following is going to City-A?
Explanation
It is known that Bus-4 is going to City-D, which means that the 2nd statement made by Bus-2 must be true, whereas the 2nd statement made by Bus-4 must be false. As the board on Bus-1 says that Bus-1 and Bus-3 are both going to City-A, Bus-1 cannot be the bus having both the boards with correct information, as each bus is going to exactly one city. This means that only Bus-3 can have both the boards with correct information, as there must be at least one bus having both boards that give correct information.
We can take this as the basis and get the arrangement as given below:
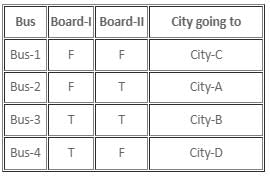
Hence, Bus-2 is going to City-A.
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the following information and answer the question that follows.
There are four buses, Bus-1, Bus-2, Bus-3, and Bus-4, standing at a bus stop. Each of the bus is going to exactly one city amongst City-A, City-B, City-C, and City-D. No bus is going to two cities. There are two boards on each bus which tell us about where the bus is going. It is known that there is at least one bus among them, on which both the boards are giving correct information, and at least one bus on which both the boards are giving false information. There is at least one bus on which at least one board is giving true information and the other board is giving false information, in any order.
One of the commuters read all the boards on the 4 buses and noted down the information as shown in the given table.
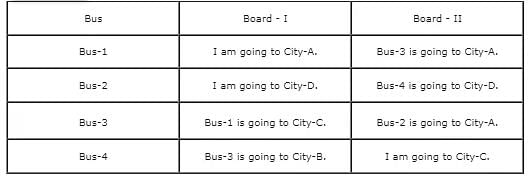
Further, on enquiry by the commuter, someone told him that Bus-4 is going to City-D, and a definite arrangement can be obtained from the information written on each bus.
Which among the following buses has both the boards that give false information?
Explanation
It is known that Bus-4 is going to City-D, which means that the 2nd statement made by Bus-2 must be true, whereas the 2nd statement made by Bus-4 must be false. As the board on Bus-1 says that Bus-1 and Bus-3 are both going to City-A, Bus-1 cannot be the bus having both the boards with correct information, as each bus is going to exactly one city. This means that only Bus-3 can have both the boards with correct information, as there must be at least one bus having both boards that give correct information.
We can take this as the basis and get the arrangement as given below:
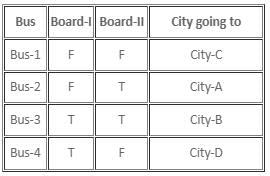
Hence, on Bus-1, both the boards are giving false information.
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the following information and answer the question that follows.
There are four buses, Bus-1, Bus-2, Bus-3, and Bus-4, standing at a bus stop. Each of the bus is going to exactly one city amongst City-A, City-B, City-C, and City-D. No bus is going to two cities. There are two boards on each bus which tell us about where the bus is going. It is known that there is at least one bus among them, on which both the boards are giving correct information, and at least one bus on which both the boards are giving false information. There is at least one bus on which at least one board is giving true information and the other board is giving false information, in any order.
One of the commuters read all the boards on the 4 buses and noted down the information as shown in the given table.
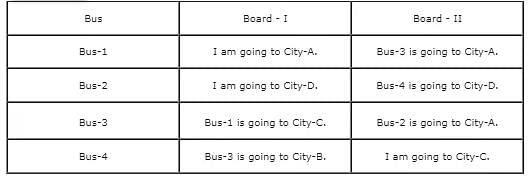
Further, on enquiry by the commuter, someone told him that Bus-4 is going to City-D, and a definite arrangement can be obtained from the information written on each bus.
Which among the following buses has one board that gives false information and the other that gives correct information?
Explanation
It is known that Bus-4 is going to City-D, which means that the 2nd statement made by Bus-2 must be true, whereas the 2nd statement made by Bus-4 must be false. As the board on Bus-1 says that Bus-1 and Bus-3 are both going to City-A, Bus-1 cannot be the bus having both the boards with correct information, as each bus is going to exactly one city. This means that only Bus-3 can have both the boards with correct information, as there must be at least one bus having both boards that give correct information.
We can take this as the basis and get the arrangement as given below:
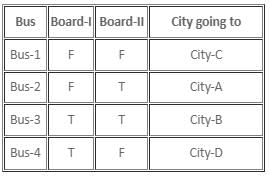
Hence, option (4) is the answer.
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the given information and answer the question that follows.
Each of three persons, Josh, Frank and Philip, is from a different locality among L-1, the L-2 and the L-3 of same constituency. Further, each person voted for a different candidate among C-1, C-2 and C-3. They made the following statements about the localities they are from and the candidates they have voted for. Further, it is known that each person told exactly one true statement.
Josh:
I am not from L-1.
Frank voted for C-3.
Philip is from the L-3.
Frank:
I voted for C-2.
Philip is not from L-3.
Josh voted for C-3.
Philip:
Josh voted for C-2.
Frank is from L-3.
I voted for C-3.
Which locality is the person who voted for C-2 from?
Explanation
Given that every person spoke exactly one true statement. Let the first statement of Josh be true. Hence, the other two must be false. Therefore, Josh is not from L-1. Frank did not vote for C-3 and Philip is not from the L-3.
Frank's second statement is, therefore, true. Hence, his first and third statements must be false. Hence, Frank did not vote for C-2 and Josh did not vote for C-3. Frank must have voted for C-1. Josh should have voted for C-2. Philip must have voted to C-3.
Hence, Philip's last statement is true. But Philip's first statement is also true. Since this is not possible, Josh' first statement cannot be true.
Let the second statement of Josh be true. Therefore, Frank voted for C-3. From his other two statements we can say that Josh is from L-1 and Philip is from L-2. Hence, Frank is from L-3. Frank's second statement is true. His first and third statements are false.
Philip's second statement is true. His first and third statements must be false. Therefore, Josh must have voted for C-1 and Philip must have voted for C-2. This is one possible case.
Let Josh's third statement be true. Philip must be from L-3. From his first statement, we get that Josh must be from L-1. Therefore, Frank must be from L-2. Frank did not vote for C-3.
Frank's second statement and Philip's second statement are false. The only case possible in which both Josh and Philip tell one true statement each is when Frank's first statement and Philip's third statement are true. Hence, Frank voted for C-2, Philip voted for C-3 and Josh voted for C-1. This is another possible case.
The possible case:

The person who voted for C-2 is from L-2.
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the given information and answer the question that follows.
Each of three persons, Josh, Frank and Philip, is from a different locality among L-1, the L-2 and the L-3 of same constituency. Further, each person voted for a different candidate among C-1, C-2 and C-3. They made the following statements about the localities they are from and the candidates they have voted for. Further, it is known that each person told exactly one true statement.
Josh:
I am not from L-1.
Frank voted for C-3.
Philip is from the L-3.
Frank:
I voted for C-2.
Philip is not from L-3.
Josh voted for C-3.
Philip:
Josh voted for C-2.
Frank is from L-3.
I voted for C-3.
The person from the L-3, voted for which candidate?
Explanation
Given that every person spoke exactly one true statement. Let the first statement of Josh be true. Hence, the other two must be false. Therefore, Josh is not from L-1. Frank did not vote for C-3 and Philip is not from the L-3.
Frank's second statement is, therefore, true. Hence, his first and third statements must be false. Hence, Frank did not vote for C-2 and Josh did not vote for C-3. Frank must have voted for C-1. Josh should have voted for C-2. Philip must have voted to C-3.
Hence, Philip's last statement is true. But Philip's first statement is also true. Since this is not possible, Josh' first statement cannot be true.
Let the second statement of Josh be true. Therefore, Frank voted for C-3. From his other two statements we can say that Josh is from L-1 and Philip is from L-2. Hence, Frank is from L-3. Frank's second statement is true. His first and third statements are false.
Philip's second statement is true. His first and third statements must be false. Therefore, Josh must have voted for C-1 and Philip must have voted for C-2. This is one possible case.
Let Josh's third statement be true. Philip must be from L-3. From his first statement, we get that Josh must be from L-1. Therefore, Frank must be from L-2. Frank did not vote for C-3.
Frank's second statement and Philip's second statement are false. The only case possible in which both Josh and Philip tell one true statement each is when Frank's first statement and Philip's third statement are true. Hence, Frank voted for C-2, Philip voted for C-3 and Josh voted for C-1. This is another possible case.
The possible case:
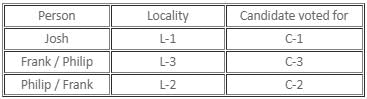
The person from L-3, voted for C-3.
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the given information and answer the question that follows.
Each of three persons, Josh, Frank and Philip, is from a different locality among L-1, the L-2 and the L-3 of same constituency. Further, each person voted for a different candidate among C-1, C-2 and C-3. They made the following statements about the localities they are from and the candidates they have voted for. Further, it is known that each person told exactly one true statement.
Josh:
I am not from L-1.
Frank voted for C-3.
Philip is from the L-3.
Frank:
I voted for C-2.
Philip is not from L-3.
Josh voted for C-3.
Philip:
Josh voted for C-2.
Frank is from L-3.
I voted for C-3.
Which locality is Frank from?
Explanation
Given that every person spoke exactly one true statement. Let the first statement of Josh be true. Hence, the other two must be false. Therefore, Josh is not from L-1. Frank did not vote for C-3 and Philip is not from the L-3.
Frank's second statement is, therefore, true. Hence, his first and third statements must be false. Hence, Frank did not vote for C-2 and Josh did not vote for C-3. Frank must have voted for C-1. Josh should have voted for C-2. Philip must have voted to C-3.
Hence, Philip's last statement is true. But Philip's first statement is also true. Since this is not possible, Josh' first statement cannot be true.
Let the second statement of Josh be true. Therefore, Frank voted for C-3. From his other two statements we can say that Josh is from L-1 and Philip is from L-2. Hence, Frank is from L-3. Frank's second statement is true. His first and third statements are false.
Philip's second statement is true. His first and third statements must be false. Therefore, Josh must have voted for C-1 and Philip must have voted for C-2. This is one possible case.
Let Josh's third statement be true. Philip must be from L-3. From his first statement, we get that Josh must be from L-1. Therefore, Frank must be from L-2. Frank did not vote for C-3.
Frank's second statement and Philip's second statement are false. The only case possible in which both Josh and Philip tell one true statement each is when Frank's first statement and Philip's third statement are true. Hence, Frank voted for C-2, Philip voted for C-3 and Josh voted for C-1. This is another possible case.
The possible case:
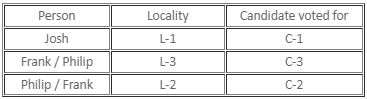
Frank can be from L-3 or L-2.
Report a problem
Question for Practice Questions Level 3: Binary Logic
Try yourself:Directions: Study the given information and answer the question that follows.
Each of three persons, Josh, Frank and Philip, is from a different locality among L-1, the L-2 and the L-3 of same constituency. Further, each person voted for a different candidate among C-1, C-2 and C-3. They made the following statements about the localities they are from and the candidates they have voted for. Further, it is known that each person told exactly one true statement.
Josh:
I am not from L-1.
Frank voted for C-3.
Philip is from the L-3.
Frank:
I voted for C-2.
Philip is not from L-3.
Josh voted for C-3.
Philip:
Josh voted for C-2.
Frank is from L-3.
I voted for C-3.
Which of the following statements is/are definitely true?
Explanation
Given that every person spoke exactly one true statement. Let the first statement of Josh be true. Hence, the other two must be false. Therefore, Josh is not from L-1. Frank did not vote for C-3 and Philip is not from the L-3.
Frank's second statement is, therefore, true. Hence, his first and third statements must be false. Hence, Frank did not vote for C-2 and Josh did not vote for C-3. Frank must have voted for C-1. Josh should have voted for C-2. Philip must have voted to C-3.
Hence, Philip's last statement is true. But Philip's first statement is also true. Since this is not possible, Josh' first statement cannot be true.
Let the second statement of Josh be true. Therefore, Frank voted for C-3. From his other two statements we can say that Josh is from L-1 and Philip is from L-2. Hence, Frank is from L-3. Frank's second statement is true. His first and third statements are false.
Philip's second statement is true. His first and third statements must be false. Therefore, Josh must have voted for C-1 and Philip must have voted for C-2. This is one possible case.
Let Josh's third statement be true. Philip must be from L-3. From his first statement, we get that Josh must be from L-1. Therefore, Frank must be from L-2. Frank did not vote for C-3.
Frank's second statement and Philip's second statement are false. The only case possible in which both Josh and Philip tell one true statement each is when Frank's first statement and Philip's third statement are true. Hence, Frank voted for C-2, Philip voted for C-3 and Josh voted for C-1. This is another possible case.
The possible case:
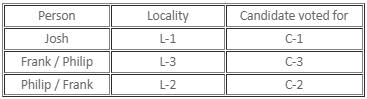
Only statements (1) and (3) are definitely true.
Report a problem







































