This EduRev document offers 15 Multiple Choice Questions (MCQs) from the topic Critical Path (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
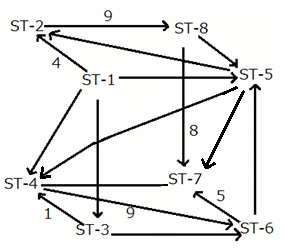
The given network diagram consists of eight railway stations, where railway station ST–1 represents a railway junction, and the rest represent other stations. The railway lines connecting the various railway stations, represent the tracks on which the trains run and the arrows indicate the direction of trains on tracks. The numbers mentioned alongside some of the arrows indicate the number of trains running on a track on any particular day. It is known that ST–2, ST–3, ST–4, ST–5, ST–6, and ST–8 are just for passage of trains and ST–7 is the only stop at which the journey ends.
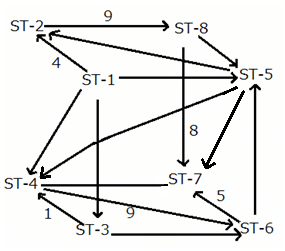
The following additional information is known:
No two railway tracks connected to a railway station have the same number of trains running through them in a day.' The number of trains running through each railway track in a day is a positive integer less than 10. The train running on the railway track connecting ST–3 and ST–6 is the least possible number.
What is the total number of trains starting from ST-1?
Explanation
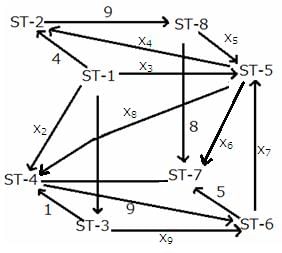
It is given that the journey ends at ST-7.
So, at every other railway station, the number of trains entering the railway station equals the number of trains leaving the railway station.
At ST-8,
x5 + 8 = 9
x5 = 1
At ST-2,
4 + x4 = 9
x4 = 5
It is given that the flow from ST-3 to ST-6 is the minimum possible.
x9 = 2
At ST-6,
x9 + 9 = x7 + 5
x7 = 6
The network now appears as below,
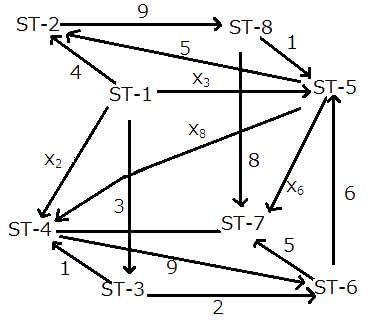
At ST-4,
x2 + x8 + 1 = 9
x2 + x8 = 8
But, x2 cannot take values of 3, 4, 1, or 9 (otherwise, it violates the 1st condition given).
Similarly, x8 cannot take 6, 5, 1, 8, or 9.
The possibilities are
x2: 5, 6
x8: 3, 2
At ST-5,
x3 + 6 + 1 = x6 + x8 + 5
x3 + 2 = x6 + x8
From the earlier result, x8 can only have the value 3 or 2.
If x8 is 2, then x3 = x6 which violates the given condition.
x8 = 3
x2 = 5
x3 + 2 = x6 + 3
x3 = x6 + 1
But, x3 and x6 cannot be 1, 2, 3, 4, 5, 6, and x6 also cannot be 8.
The only possibility is x6 = 7 and x3 = 8.
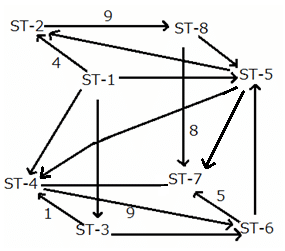
Hence, a total of 20 trains start from ST-1.
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
The given network diagram consists of eight railway stations, where railway station ST–1 represents a railway junction, and the rest represent other stations. The railway lines connecting the various railway stations, represent the tracks on which the trains run and the arrows indicate the direction of trains on tracks. The numbers mentioned alongside some of the arrows indicate the number of trains running on a track on any particular day. It is known that ST–2, ST–3, ST–4, ST–5, ST–6, and ST–8 are just for passage of trains and ST–7 is the only stop at which the journey ends.
The following additional information is known:
No two railway tracks connected to a railway station have the same number of trains running through them in a day.' The number of trains running through each railway track in a day is a positive integer less than 10. The train running on the railway track connecting ST–3 and ST–6 is the least possible number.
How many trains go from ST-1 to ST-5?
Explanation
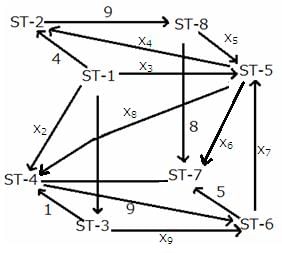
It is given that the journey ends at ST-7.
So, at every other railway station, the number of trains entering the railway station equals the number of trains leaving the railway station.
At ST-8,
x5 + 8 = 9
x5 = 1
At ST-2,
4 + x4 = 9
x4 = 5
It is given that the flow from ST-3 to ST-6 is the minimum possible.
x9 = 2
At ST-6,
x9 + 9 = x7 + 5
x7 = 6
The network now appears as below,
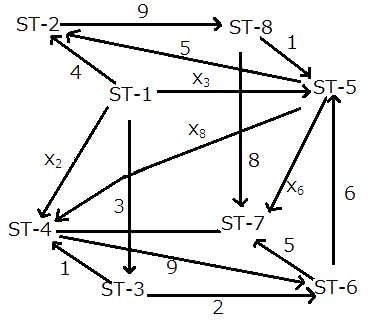
At ST-4,
x2 + x8 + 1 = 9
x2 + x8 = 8
But, x2 cannot take values of 3, 4, 1, or 9 (otherwise, it violates the 1st condition given).
Similarly, x8 cannot take 6, 5, 1, 8, or 9.
The possibilities are
x2: 5, 6
x8: 3, 2
At ST-5,
x3 + 6 + 1 = x6 + x8 + 5
x3 + 2 = x6 + x8
From the earlier result, x8 can only have the value 3 or 2.
If x8 is 2, then x3 = x6 which violates the given condition.
x8 = 3
x2 = 5
x3 + 2 = x6 + 3
x3 = x6 + 1
But, x3 and x6 cannot be 1, 2, 3, 4, 5, 6, and x6 also cannot be 8.
The only possibility is x6 = 7 and x3 = 8.
Hence, 8 trains go from ST-1 to ST-5.
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
The given network diagram consists of eight railway stations, where railway station ST–1 represents a railway junction, and the rest represent other stations. The railway lines connecting the various railway stations, represent the tracks on which the trains run and the arrows indicate the direction of trains on tracks. The numbers mentioned alongside some of the arrows indicate the number of trains running on a track on any particular day. It is known that ST–2, ST–3, ST–4, ST–5, ST–6, and ST–8 are just for passage of trains and ST–7 is the only stop at which the journey ends.

The following additional information is known:
No two railway tracks connected to a railway station have the same number of trains running through them in a day.' The number of trains running through each railway track in a day is a positive integer less than 10. The train running on the railway track connecting ST–3 and ST–6 is the least possible number.
Which of the following statements is/are true?
Statement 1: The number of trains between ST-5 and ST-6 is 8.
Statement 2: The number of trains between ST-5 and ST-4 is more than 2.
Explanation
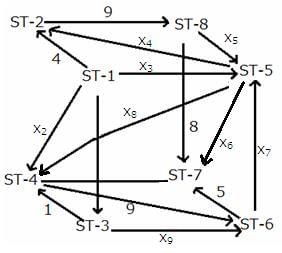
It is given that the journey ends at ST-7.
So, at every other railway station, the number of trains entering the railway station equals the number of trains leaving the railway station.
At ST-8,
x5 + 8 = 9
x5 = 1
At ST-2,
4 + x4 = 9
x4 = 5
It is given that the flow from ST-3 to ST-6 is the minimum possible.
x9 = 2
At ST-6,
x9 + 9 = x7 + 5
x7 = 6
The network now appears as below,
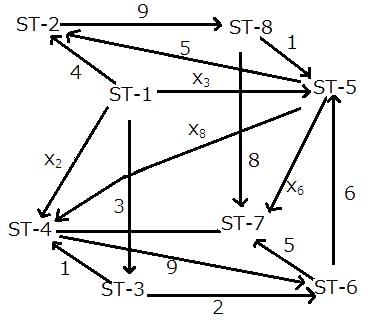
At ST-4,
x2 + x8 + 1 = 9
x2 + x8 = 8
But, x2 cannot take values of 3, 4, 1, or 9 (otherwise, it violates the 1st condition given).
Similarly, x8 cannot take 6, 5, 1, 8, or 9.
The possibilities are
x2: 5, 6
x8: 3, 2
At ST-5,
x3 + 6 + 1 = x6 + x8 + 5
x3 + 2 = x6 + x8
From the earlier result, x8 can only have the value 3 or 2.
If x8 is 2, then x3 = x6 which violates the given condition.
x8 = 3
x2 = 5
x3 + 2 = x6 + 3
x3 = x6 + 1
But, x3 and x6 cannot be 1, 2, 3, 4, 5, 6, and x6 also cannot be 8.
The only possibility is x6 = 7 and x3 = 8.
Statement 1: It is false because only 6 trains go from ST-5 to ST-6.
Statement 2: It is true as the number of trains going from ST-5 to ST-4 is 3.
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
The given network diagram consists of eight railway stations, where railway station ST–1 represents a railway junction, and the rest represent other stations. The railway lines connecting the various railway stations, represent the tracks on which the trains run and the arrows indicate the direction of trains on tracks. The numbers mentioned alongside some of the arrows indicate the number of trains running on a track on any particular day. It is known that ST–2, ST–3, ST–4, ST–5, ST–6, and ST–8 are just for passage of trains and ST–7 is the only stop at which the journey ends.
The following additional information is known:
No two railway tracks connected to a railway station have the same number of trains running through them in a day.' The number of trains running through each railway track in a day is a positive integer less than 10. The train running on the railway track connecting ST–3 and ST–6 is the least possible number.
Between which of the following pairs of railway tracks is the number of trains running the same?
Explanation
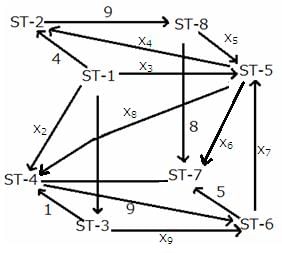
It is given that the journey ends at ST-7.
So, at every other railway station, the number of trains entering the railway station equals the number of trains leaving the railway station.
At ST-8,
x5 + 8 = 9
x5 = 1
At ST-2,
4 + x4 = 9
x4 = 5
It is given that the flow from ST-3 to ST-6 is the minimum possible.
x9 = 2
At ST-6,
x9 + 9 = x7 + 5
x7 = 6
The network now appears as below,

At ST-4,
x2 + x8 + 1 = 9
x2 + x8 = 8
But, x2 cannot take values of 3, 4, 1, or 9 (otherwise, it violates the 1st condition given).
Similarly, x8 cannot take 6, 5, 1, 8, or 9.
The possibilities are
x2: 5, 6
x8: 3, 2
At ST-5,
x3 + 6 + 1 = x6 + x8 + 5
x3 + 2 = x6 + x8
From the earlier result, x8 can only have the value 3 or 2.
If x8 is 2, then x3 = x6 which violates the given condition.
x8 = 3
x2 = 5
x3 + 2 = x6 + 3
x3 = x6 + 1
But, x3 and x6 cannot be 1, 2, 3, 4, 5, 6, and x6 also cannot be 8.
The only possibility is x6 = 7 and x3 = 8.
The number of trains in the railway track connecting ST-5 and ST-4 and that in the track connecting ST-1 and ST-3 is the same, i.e. 3.
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
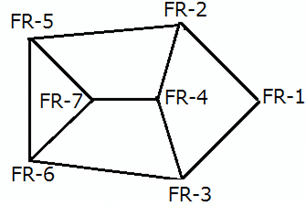
A spy of XYZ kingdom regularly spies between seven enemy camps that are located inside a forest, and are connected to each other by forest roads, FR–1, FR–2, FR–3, FR–4, FR–5, FR–6, and FR–7. The spy has made a map so that he can travel with ease between camps and get the useful information required. However, while travelling between any two enemy camps, the spy always chooses the route which passes through the minimum possible number of enemy camps. If two or more routes pass through the minimum number of enemy camps, he chooses the route for which the distance is also the least. The length of the forest road, directly connecting any two enemy camps, is a multiple of 10. For any pair of enemy camps, the length of a route connecting the two enemy camps and passing through the minimum possible number of enemy camps, is called a forest road stretch between the two enemy camps. The least among all the forest road stretches between two enemy camps is called the minimum forest road stretch between the two enemy camps.
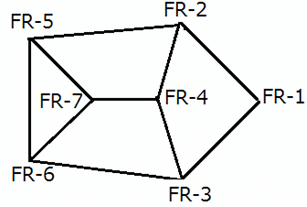
The following information is known about the distances between the enemy camps:
1. The minimum forest road stretch between FR–4 and FR–6 is 90 miles, while the minimum forest road stretch between FR–2 and FR–6 is 30 miles.
2. The highest forest road stretch between FR–1 and FR–7 is 360 miles.
3. The minimum forest road stretch between FR–4 and FR–7 is 30 miles.
4. The sum of the lengths of the road directly connecting FR–5 to FR–6 and that directly connecting FR–5 and FR–7 is 100 miles.
5. The minimum forest road stretch between FR–7 and FR–2 is 70 miles, while the minimum forest road stretch between FR–3 and FR–7 is 110 miles.
6. The length of the road directly connecting FR–3 and FR–6 is greater than 110 miles.
7. The minimum forest road stretch between FR–1 and FR–4 is 110 miles, while the highest forest road stretch between FR–2 and FR–3 is 240 miles.
If the spy has to travel from FR-1 to FR-7, the distance (in miles) that the spy would have to cover is
Explanation
Let the length of the roads be as shown below.
From (iii), we have FR-4 - FR-7 = g = 30, and from (vi), we have FR-3 - FR-6 = f > 110
From (i), FR-4 - FR-6 = 90
The possible routes are FR-4 - FR-7 - FR-6 and FR-4 - FR-3 - FR-6.
For the route FR-4 - FR-7 - FR-6,
g + i = 90
For the route FR-4 - FR-3 - FR-6,
d + f = 90
But, this is not possible since the value of f is greater than 110.
Therefore, the route FR-4 - FR-7 - FR-6 is taken.
Now, g + i = 90 ⇒ i = 60
From (i), FR-2 - FR-6 = 30
Shortest route is FR-2 - FR-5 - FR-6, i.e.
e + j = 30 ⇒ (e, j) = (10, 20) or (20, 10)
From (v), FR-3 - FR-7 = 110
The possible routes are FR-3 - FR-4 - FR-7 and FR-3 - FR-6 - FR-7.
For the route FR-3 - FR-4 - FR-7,
d + g = 110
For the route FR-3 - FR-6 - FR-7,
i + f = 110
But, this is not possible since the value of f is greater than 110.
Therefore, the route FR-3 - FR-4 - FR-7 is taken.
Now, d + g = 110 ⇒ d = 80
From (iv), FR-5 - FR-6 + FR-5 - FR-7 = 100, i.e.
h + j = 100
Since j can only be 20 or 10, the possibilities for (h, j) are only (90, 10) and (80, 20).
But the lengths 80, 30, and 60 are already taken, and the length of the roads are distinct integers. So, the only possible case, (h, j) = (90, 10), implies e = 20.
From (v), FR-7 - FR-2 = 70
The possible routes are FR-7 - FR-4 - FR-2 and FR-7 - FR-5 - FR-2.
For the route FR-7 - FR-4 - FR-2,
g + c =70 ⇒ c = 40
For the route FR-7 - FR-5 - FR-2,
e + h = 70
But, this is not possible since the value of e + h is 110.
Therefore, for FR-7 - FR-2, the route FR-7 - FR-4 - FR-2 is taken.
From (vii), FR-1 - FR-4 = 110
The possible routes are FR-1 - FR-2 - FR-4 and FR-1 - FR-3 - FR-4.
For the route FR-1 - FR-2 - FR-4,
a + c = 110
⇒ a = 70
For the route FR-1 - FR-3 - FR-4,
b + d = 110
b = 110 - 80 = 30
But, this is not possible since the length of each road is unique.
Therefore, the route FR-1 - FR-2 - FR-4 is taken.
From (vii), FR-2 - FR-3 = 240
The possible routes are FR-2 - FR-1 - FR-3 and FR-2 - FR-4 - FR-3.
For the route FR-2 - FR-1 - FR-3,
a + b = 240
b = 170
For the route FR-2 - FR-4 - FR-3,
c + d = 240
But, this is not possible since the value of c + d is 120.
Therefore, the route FR-2 - FR-1 - FR-3 is taken.
From (ii), FR-1 - FR-7 = 360 (Longest path)
The possible routes for this are FR-1 - FR-2 - FR-4 - FR-7.
a + c + g = 360
But a + c + g = 140
This is not the longest path.
FR-1 - FR-2 - FR-5 - FR-7
a + e + h = 360
But, a + e + h = 180 (Not the longest path)
FR-1 - FR-3 - FR-4 - FR-7
b + d + g= 360
But b + d + g = 280 (Not the longest path)
The only possibility is FR-1 - FR-3 - FR-6 - FR-7.
b + f + i = 360
f = 130
The final network is as follows:
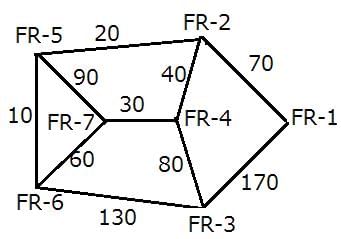
The spy would take the shortest path from FR-1 - FR-7, which is FR-1- FR-2 - FR-4 - FR-7.
Length of the shortest path = 70 + 40 + 30 = 140
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
A spy of XYZ kingdom regularly spies between seven enemy camps that are located inside a forest, and are connected to each other by forest roads, FR–1, FR–2, FR–3, FR–4, FR–5, FR–6, and FR–7. The spy has made a map so that he can travel with ease between camps and get the useful information required. However, while travelling between any two enemy camps, the spy always chooses the route which passes through the minimum possible number of enemy camps. If two or more routes pass through the minimum number of enemy camps, he chooses the route for which the distance is also the least. The length of the forest road, directly connecting any two enemy camps, is a multiple of 10. For any pair of enemy camps, the length of a route connecting the two enemy camps and passing through the minimum possible number of enemy camps, is called a forest road stretch between the two enemy camps. The least among all the forest road stretches between two enemy camps is called the minimum forest road stretch between the two enemy camps.
The following information is known about the distances between the enemy camps:
1. The minimum forest road stretch between FR–4 and FR–6 is 90 miles, while the minimum forest road stretch between FR–2 and FR–6 is 30 miles.
2. The highest forest road stretch between FR–1 and FR–7 is 360 miles.
3. The minimum forest road stretch between FR–4 and FR–7 is 30 miles.
4. The sum of the lengths of the road directly connecting FR–5 to FR–6 and that directly connecting FR–5 and FR–7 is 100 miles.
5. The minimum forest road stretch between FR–7 and FR–2 is 70 miles, while the minimum forest road stretch between FR–3 and FR–7 is 110 miles.
6. The length of the road directly connecting FR–3 and FR–6 is greater than 110 miles.
7. The minimum forest road stretch between FR–1 and FR–4 is 110 miles, while the highest forest road stretch between FR–2 and FR–3 is 240 miles.
Between which of the following pairs of enemy camps is the minimum forest road stretch the least?
Explanation
Let the length of the roads be as shown below.
From (iii), we have FR-4 - FR-7 = g = 30, and from (vi), we have FR-3 - FR-6 = f > 110
From (i), FR-4 - FR-6 = 90
The possible routes are FR-4 - FR-7 - FR-6 and FR-4 - FR-3 - FR-6.
For the route FR-4 - FR-7 - FR-6,
g + i = 90
For the route FR-4 - FR-3 - FR-6,
d + f = 90
But, this is not possible since the value of f is greater than 110.
Therefore, the route FR-4 - FR-7 - FR-6 is taken.
Now, g + i = 90 ⇒ i = 60
From (i), FR-2 - FR-6 = 30
Shortest route is FR-2 - FR-5 - FR-6, i.e.
e + j = 30 ⇒ (e, j) = (10, 20) or (20, 10)
From (v), FR-3 - FR-7 = 110
The possible routes are FR-3 - FR-4 - FR-7 and FR-3 - FR-6 - FR-7.
For the route FR-3 - FR-4 - FR-7,
d + g = 110
For the route FR-3 - FR-6 - FR-7,
i + f = 110
But, this is not possible since the value of f is greater than 110.
Therefore, the route FR-3 - FR-4 - FR-7 is taken.
Now, d + g = 110 ⇒ d = 80
From (iv), FR-5 - FR-6 + FR-5 - FR-7 = 100, i.e.
h + j = 100
Since j can only be 20 or 10, the possibilities for (h, j) are only (90, 10) and (80, 20).
But the lengths 80, 30, and 60 are already taken, and the length of the roads are distinct integers. So, the only possible case, (h, j) = (90, 10), implies e = 20.
From (v), FR-7 - FR-2 = 70
The possible routes are FR-7 - FR-4 - FR-2 and FR-7 - FR-5 - FR-2.
For the route FR-7 - FR-4 - FR-2,
g + c =70 ⇒ c = 40
For the route FR-7 - FR-5 - FR-2,
e + h = 70
But, this is not possible since the value of e + h is 110.
Therefore, for FR-7 - FR-2, the route FR-7 - FR-4 - FR-2 is taken.
From (vii), FR-1 - FR-4 = 110
The possible routes are FR-1 - FR-2 - FR-4 and FR-1 - FR-3 - FR-4.
For the route FR-1 - FR-2 - FR-4,
a + c = 110
⇒ a = 70
For the route FR-1 - FR-3 - FR-4,
b + d = 110
b = 110 - 80 = 30
But, this is not possible since the length of each road is unique.
Therefore, the route FR-1 - FR-2 - FR-4 is taken.
From (vii), FR-2 - FR-3 = 240
The possible routes are FR-2 - FR-1 - FR-3 and FR-2 - FR-4 - FR-3.
For the route FR-2 - FR-1 - FR-3,
a + b = 240
b = 170
For the route FR-2 - FR-4 - FR-3,
c + d = 240
But, this is not possible since the value of c + d is 120.
Therefore, the route FR-2 - FR-1 - FR-3 is taken.
From (ii), FR-1 - FR-7 = 360 (Longest path)
The possible routes for this are FR-1 - FR-2 - FR-4 - FR-7.
a + c + g = 360
But a + c + g = 140
This is not the longest path.
FR-1 - FR-2 - FR-5 - FR-7
a + e + h = 360
But, a + e + h = 180 (Not the longest path)
FR-1 - FR-3 - FR-4 - FR-7
b + d + g= 360
But b + d + g = 280 (Not the longest path)
The only possibility is FR-1 - FR-3 - FR-6 - FR-7.
b + f + i = 360
f = 130
The final network is as follows:
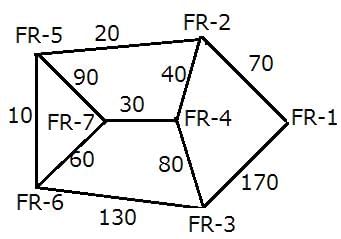
Minimum forest road stretch between:
FR-2 - FR-5 = 20
FR-5 - FR-6 = 10
FR-4 - FR-7 = 30
FR-2 - FR-3 = 120
Hence, the least stretch is between FR-5 and FR-6.
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
A spy of XYZ kingdom regularly spies between seven enemy camps that are located inside a forest, and are connected to each other by forest roads, FR–1, FR–2, FR–3, FR–4, FR–5, FR–6, and FR–7. The spy has made a map so that he can travel with ease between camps and get the useful information required. However, while travelling between any two enemy camps, the spy always chooses the route which passes through the minimum possible number of enemy camps. If two or more routes pass through the minimum number of enemy camps, he chooses the route for which the distance is also the least. The length of the forest road, directly connecting any two enemy camps, is a multiple of 10. For any pair of enemy camps, the length of a route connecting the two enemy camps and passing through the minimum possible number of enemy camps, is called a forest road stretch between the two enemy camps. The least among all the forest road stretches between two enemy camps is called the minimum forest road stretch between the two enemy camps.
The following information is known about the distances between the enemy camps:
1. The minimum forest road stretch between FR–4 and FR–6 is 90 miles, while the minimum forest road stretch between FR–2 and FR–6 is 30 miles.
2. The highest forest road stretch between FR–1 and FR–7 is 360 miles.
3. The minimum forest road stretch between FR–4 and FR–7 is 30 miles.
4. The sum of the lengths of the road directly connecting FR–5 to FR–6 and that directly connecting FR–5 and FR–7 is 100 miles.
5. The minimum forest road stretch between FR–7 and FR–2 is 70 miles, while the minimum forest road stretch between FR–3 and FR–7 is 110 miles.
6. The length of the road directly connecting FR–3 and FR–6 is greater than 110 miles.
7. The minimum forest road stretch between FR–1 and FR–4 is 110 miles, while the highest forest road stretch between FR–2 and FR–3 is 240 miles.
What is the highest forest road stretch between FR-3 and FR-7?
Explanation
Let the length of the roads be as shown below.
From (iii), we have FR-4 - FR-7 = g = 30, and from (vi), we have FR-3 - FR-6 = f > 110
From (i), FR-4 - FR-6 = 90
The possible routes are FR-4 - FR-7 - FR-6 and FR-4 - FR-3 - FR-6.
For the route FR-4 - FR-7 - FR-6,
g + i = 90
For the route FR-4 - FR-3 - FR-6,
d + f = 90
But, this is not possible since the value of f is greater than 110.
Therefore, the route FR-4 - FR-7 - FR-6 is taken.
Now, g + i = 90 ⇒ i = 60
From (i), FR-2 - FR-6 = 30
Shortest route is FR-2 - FR-5 - FR-6, i.e.
e + j = 30 ⇒ (e, j) = (10, 20) or (20, 10)
From (v), FR-3 - FR-7 = 110
The possible routes are FR-3 - FR-4 - FR-7 and FR-3 - FR-6 - FR-7.
For the route FR-3 - FR-4 - FR-7,
d + g = 110
For the route FR-3 - FR-6 - FR-7,
i + f = 110
But, this is not possible since the value of f is greater than 110.
Therefore, the route FR-3 - FR-4 - FR-7 is taken.
Now, d + g = 110 ⇒ d = 80
From (iv), FR-5 - FR-6 + FR-5 - FR-7 = 100, i.e.
h + j = 100
Since j can only be 20 or 10, the possibilities for (h, j) are only (90, 10) and (80, 20).
But the lengths 80, 30, and 60 are already taken, and the length of the roads are distinct integers. So, the only possible case, (h, j) = (90, 10), implies e = 20.
From (v), FR-7 - FR-2 = 70
The possible routes are FR-7 - FR-4 - FR-2 and FR-7 - FR-5 - FR-2.
For the route FR-7 - FR-4 - FR-2,
g + c =70 ⇒ c = 40
For the route FR-7 - FR-5 - FR-2,
e + h = 70
But, this is not possible since the value of e + h is 110.
Therefore, for FR-7 - FR-2, the route FR-7 - FR-4 - FR-2 is taken.
From (vii), FR-1 - FR-4 = 110
The possible routes are FR-1 - FR-2 - FR-4 and FR-1 - FR-3 - FR-4.
For the route FR-1 - FR-2 - FR-4,
a + c = 110
⇒ a = 70
For the route FR-1 - FR-3 - FR-4,
b + d = 110
b = 110 - 80 = 30
But, this is not possible since the length of each road is unique.
Therefore, the route FR-1 - FR-2 - FR-4 is taken.
From (vii), FR-2 - FR-3 = 240
The possible routes are FR-2 - FR-1 - FR-3 and FR-2 - FR-4 - FR-3.
For the route FR-2 - FR-1 - FR-3,
a + b = 240
b = 170
For the route FR-2 - FR-4 - FR-3,
c + d = 240
But, this is not possible since the value of c + d is 120.
Therefore, the route FR-2 - FR-1 - FR-3 is taken.
From (ii), FR-1 - FR-7 = 360 (Longest path)
The possible routes for this are FR-1 - FR-2 - FR-4 - FR-7.
a + c + g = 360
But a + c + g = 140
This is not the longest path.
FR-1 - FR-2 - FR-5 - FR-7
a + e + h = 360
But, a + e + h = 180 (Not the longest path)
FR-1 - FR-3 - FR-4 - FR-7
b + d + g= 360
But b + d + g = 280 (Not the longest path)
The only possibility is FR-1 - FR-3 - FR-6 - FR-7.
b + f + i = 360
f = 130
The final network is as follows:
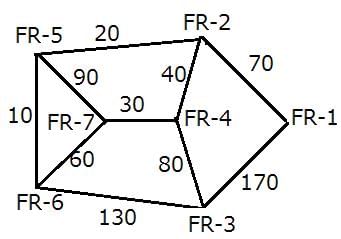
The highest forest road stretch between FR-3 and FR-7 is for the route FR-3 - FR-6 - FR-7, i.e. 130 + 60 = 190 miles.
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
A spy of XYZ kingdom regularly spies between seven enemy camps that are located inside a forest, and are connected to each other by forest roads, FR–1, FR–2, FR–3, FR–4, FR–5, FR–6, and FR–7. The spy has made a map so that he can travel with ease between camps and get the useful information required. However, while travelling between any two enemy camps, the spy always chooses the route which passes through the minimum possible number of enemy camps. If two or more routes pass through the minimum number of enemy camps, he chooses the route for which the distance is also the least. The length of the forest road, directly connecting any two enemy camps, is a multiple of 10. For any pair of enemy camps, the length of a route connecting the two enemy camps and passing through the minimum possible number of enemy camps, is called a forest road stretch between the two enemy camps. The least among all the forest road stretches between two enemy camps is called the minimum forest road stretch between the two enemy camps.
The following information is known about the distances between the enemy camps:
1. The minimum forest road stretch between FR–4 and FR–6 is 90 miles, while the minimum forest road stretch between FR–2 and FR–6 is 30 miles.
2. The highest forest road stretch between FR–1 and FR–7 is 360 miles.
3. The minimum forest road stretch between FR–4 and FR–7 is 30 miles.
4. The sum of the lengths of the road directly connecting FR–5 to FR–6 and that directly connecting FR–5 and FR–7 is 100 miles.
5. The minimum forest road stretch between FR–7 and FR–2 is 70 miles, while the minimum forest road stretch between FR–3 and FR–7 is 110 miles.
6. The length of the road directly connecting FR–3 and FR–6 is greater than 110 miles.
7. The minimum forest road stretch between FR–1 and FR–4 is 110 miles, while the highest forest road stretch between FR–2 and FR–3 is 240 miles.
The spy's companion, Mr. Y, always travels along the shortest route when travelling from one enemy camp to another. On a particular day, both, the spy and Mr. Y, started from FR-1 and reached X, which is one of the other six enemy camps. If the length of the route that the spy took is greater than that of the route that Mr. Y took, how many of the six enemy camps were there in the route of the spy?
Explanation
Let the length of the roads be as shown below.
From (iii), we have FR-4 - FR-7 = g = 30, and from (vi), we have FR-3 - FR-6 = f > 110
From (i), FR-4 - FR-6 = 90
The possible routes are FR-4 - FR-7 - FR-6 and FR-4 - FR-3 - FR-6.
For the route FR-4 - FR-7 - FR-6,
g + i = 90
For the route FR-4 - FR-3 - FR-6,
d + f = 90
But, this is not possible since the value of f is greater than 110.
Therefore, the route FR-4 - FR-7 - FR-6 is taken.
Now, g + i = 90 ⇒ i = 60
From (i), FR-2 - FR-6 = 30
Shortest route is FR-2 - FR-5 - FR-6, i.e.
e + j = 30 ⇒ (e, j) = (10, 20) or (20, 10)
From (v), FR-3 - FR-7 = 110
The possible routes are FR-3 - FR-4 - FR-7 and FR-3 - FR-6 - FR-7.
For the route FR-3 - FR-4 - FR-7,
d + g = 110
For the route FR-3 - FR-6 - FR-7,
i + f = 110
But, this is not possible since the value of f is greater than 110.
Therefore, the route FR-3 - FR-4 - FR-7 is taken.
Now, d + g = 110 ⇒ d = 80
From (iv), FR-5 - FR-6 + FR-5 - FR-7 = 100, i.e.
h + j = 100
Since j can only be 20 or 10, the possibilities for (h, j) are only (90, 10) and (80, 20).
But the lengths 80, 30, and 60 are already taken, and the length of the roads are distinct integers. So, the only possible case, (h, j) = (90, 10), implies e = 20.
From (v), FR-7 - FR-2 = 70
The possible routes are FR-7 - FR-4 - FR-2 and FR-7 - FR-5 - FR-2.
For the route FR-7 - FR-4 - FR-2,
g + c =70 ⇒ c = 40
For the route FR-7 - FR-5 - FR-2,
e + h = 70
But, this is not possible since the value of e + h is 110.
Therefore, for FR-7 - FR-2, the route FR-7 - FR-4 - FR-2 is taken.
From (vii), FR-1 - FR-4 = 110
The possible routes are FR-1 - FR-2 - FR-4 and FR-1 - FR-3 - FR-4.
For the route FR-1 - FR-2 - FR-4,
a + c = 110
⇒ a = 70
For the route FR-1 - FR-3 - FR-4,
b + d = 110
b = 110 - 80 = 30
But, this is not possible since the length of each road is unique.
Therefore, the route FR-1 - FR-2 - FR-4 is taken.
From (vii), FR-2 - FR-3 = 240
The possible routes are FR-2 - FR-1 - FR-3 and FR-2 - FR-4 - FR-3.
For the route FR-2 - FR-1 - FR-3,
a + b = 240
b = 170
For the route FR-2 - FR-4 - FR-3,
c + d = 240
But, this is not possible since the value of c + d is 120.
Therefore, the route FR-2 - FR-1 - FR-3 is taken.
From (ii), FR-1 - FR-7 = 360 (Longest path)
The possible routes for this are FR-1 - FR-2 - FR-4 - FR-7.
a + c + g = 360
But a + c + g = 140
This is not the longest path.
FR-1 - FR-2 - FR-5 - FR-7
a + e + h = 360
But, a + e + h = 180 (Not the longest path)
FR-1 - FR-3 - FR-4 - FR-7
b + d + g= 360
But b + d + g = 280 (Not the longest path)
The only possibility is FR-1 - FR-3 - FR-6 - FR-7.
b + f + i = 360
f = 130
The final network is as follows:
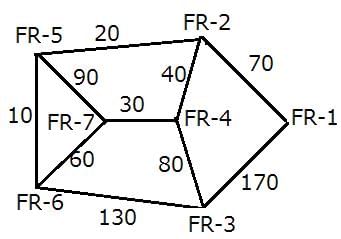
The minimum forest road stretch should be more than the length of the shortest routes. For FR-2, FR-3, FR-4, FR-5 and FR-7, the distance along the shortest route & minimum forest road stretch is the same. However, for FR-6, the shortest route is FR-1 - FR-2 - FR-5 - FR-6, which has a length of 100 miles. But this route will not pass through the minimum number of enemy camps. Hence, the spy would have travelled through the route FR-1 - FR-3 - FR-6, covering a total of 300 miles, with only one enemy camp in the route.
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
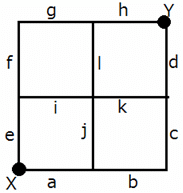
In a hamster running game, starting point X and end point Y are connected by a grid of 12 hamster running tracks, all of same length, numbered ''a'' to ''l'', as shown below. The meeting point of two or more tracks is called a track meeting point (TMP), represented by ''z'', where 'z' is the number of tracks meeting at that point. However, X and Y are not TMPs as they are the start and end points.
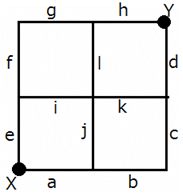
Six hamsters, H1, H2, H3, H4, H5, and H6, started at the same time from X, and ran to Y at the same speed. No two hamsters ran together for the entire track, and each hamster ran along a route of the minimum possible length. It is also known that H2 and H3 did not travel through the four-track TMP, while H4 ran alongside H6 on track-k, and H3 ran alongside H5 on track-h.
If H6 and H1 did not come across each other, except at the four-track TMP, then the number of tracks along which H4 ran alongside H2 is at most
Explanation
As each hamster traveled along a route of minimum possible distance, each one of them should have traveled along the routes which use exactly four tracks. The number of such routes, as given below, are 6.
Route (i): H2 : a-b-c-d
Route (ii) : H4/H6 : a-j-k-d
Route (iii) : H1/H5 : a-j-l-h
Route (iv) : H3 : e-f-g-h
Route (v) : H1/H5 : e-i-l-h
Route (vi) : H4/H6 : e-i-k-d
As H2 and H3 didn't cross the four-track TMP, they should have taken either route (i) or route (iv), and as H3 and H5 ran on track-h, H3 must have used route (iv) and H2 must have used route (i).
As H4 ran alongside H6 on track-k, they must have used route (ii) and route (vi), in any order. H5 and H1 must have used route (iii) and route (iv) in any order. Thus, the data can be tabulated as follows:

H6 and H1 did not come across each other, except at the four track TMP. This is possible only if (a) H6 used route (ii) and H1 used route (v), or (b) H6 used route (vi) and H1 used route (iii).
In the first case, H4 used route (vi) and ran alongside H2 on one track. In the second case, H4 used route (ii) and ran alongside H2 on two tracks. Hence, the maximum possible number of tracks is two.
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
In a hamster running game, starting point X and end point Y are connected by a grid of 12 hamster running tracks, all of same length, numbered ''a'' to ''l'', as shown below. The meeting point of two or more tracks is called a track meeting point (TMP), represented by ''z'', where 'z' is the number of tracks meeting at that point. However, X and Y are not TMPs as they are the start and end points.
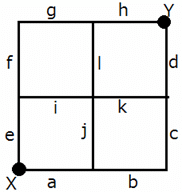
Six hamsters, H1, H2, H3, H4, H5, and H6, started at the same time from X, and ran to Y at the same speed. No two hamsters ran together for the entire track, and each hamster ran along a route of the minimum possible length. It is also known that H2 and H3 did not travel through the four-track TMP, while H4 ran alongside H6 on track-k, and H3 ran alongside H5 on track-h.
If track-i and track-k were closed due to damage and some of the hamsters changed their routes in a manner such that no three hamsters ran together for the entire journey (instead of no two hamsters, as mentioned above), then what would be the difference between the number of hamsters who used track-h and the number of hamsters who used track-d?
Explanation
As each hamster traveled along a route of minimum possible distance, each one of them should have traveled along the routes which use exactly four tracks. The number of such routes, as given below, are 6.
Route (i): H2 : a-b-c-d
Route (ii) : H4/H6 : a-j-k-d
Route (iii) : H1/H5 : a-j-l-h
Route (iv) : H3 : e-f-g-h
Route (v) : H1/H5 : e-i-l-h
Route (vi) : H4/H6 : e-i-k-d
As H2 and H3 didn't cross the four-track TMP, they should have taken either route (i) or route (iv), and as H3 and H5 ran on track-h, H3 must have used route (iv) and H2 must have used route (i).
As H4 ran alongside H6 on track-k, they must have used route (ii) and route (vi), in any order. H5 and H1 must have used route (iii) and route (iv) in any order. Thus, the data can be tabulated as follows:

If track-i and track-k were closed, then the routes (ii), (v) and (vi) could not have been used. As there are three routes and 6 hamsters, and as three hamsters could not have travelled together for the entire journey, each route should have been used by exactly two hamsters. Hamsters that used routes (iii) and (iv), used track-h and hamsters that used route (i), used track-d.
Hence, required difference = (2 × 2) - (1 × 2) = 2
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
In a hamster running game, starting point X and end point Y are connected by a grid of 12 hamster running tracks, all of same length, numbered ''a'' to ''l'', as shown below. The meeting point of two or more tracks is called a track meeting point (TMP), represented by ''z'', where 'z' is the number of tracks meeting at that point. However, X and Y are not TMPs as they are the start and end points.
Six hamsters, H1, H2, H3, H4, H5, and H6, started at the same time from X, and ran to Y at the same speed. No two hamsters ran together for the entire track, and each hamster ran along a route of the minimum possible length. It is also known that H2 and H3 did not travel through the four-track TMP, while H4 ran alongside H6 on track-k, and H3 ran alongside H5 on track-h.
Which of the following statements is definitely true?
Explanation
As each hamster traveled along a route of minimum possible distance, each one of them should have traveled along the routes which use exactly four tracks. The number of such routes, as given below, are 6.
Route (i): H2 : a-b-c-d
Route (ii) : H4/H6 : a-j-k-d
Route (iii) : H1/H5 : a-j-l-h
Route (iv) : H3 : e-f-g-h
Route (v) : H1/H5 : e-i-l-h
Route (vi) : H4/H6 : e-i-k-d
As H2 and H3 didn't cross the four-track TMP, they should have taken either route (i) or route (iv), and as H3 and H5 ran on track-h, H3 must have used route (iv) and H2 must have used route (i).
As H4 ran alongside H6 on track-k, they must have used route (ii) and route (vi), in any order. H5 and H1 must have used route (iii) and route (iv) in any order. Thus, the data can be tabulated as follows:

As we can see that the tracks used by H4/H6 are not dependent on the tracks used by H1/H5, options (2) and (4) can be eliminated as nothing can be concluded from them. If H4 used route (v), he must have used track-e. In such a case, H6 used route (ii) and didn't use track-i. Hence, option (1) is false. If H6 ran on route (ii), he must have used track-a. Then, H4 ran on route (vi) and used track-e. Hence, option (3) is definitely true.
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
Given below is a network of high tension wires from power plant (PP) and 8 transformers T1 to T8. The requirement of power by transformer is exactly met by the electric power provided by the power plant. The electric power in some of the high tension wires and the requirement at some of the transformers has also been mentioned. PP is the source transformer, i.e. the PP does not have any requirement of its own, but it supplies the requirements of all the other transformers.(All values shown in the figure are in KW.)
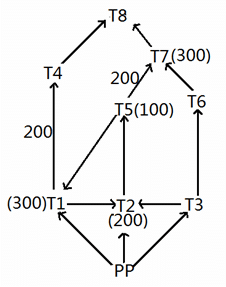
It is also known that:
i. The maximum capacity of any high tension wire is 1000 KW.
ii. The requirement at any transformer, except the power plant and T8, is equal to the flow in exactly one of the high tension wires directly connected to it.
iii. No two high tension wires, directly connected to the same transformer, carry the same amount of electric power.
iv. The flow in none of the high tension wires shown above is zero.
What is the requirement of power (in KW) at the transformer T8?
Explanation
As no two high tension wires connecting the same place are carrying same amount of electric power, and at least one of the high tension wires should carry same as that of the place, either T7-T8 or T6-T7 must carry 300 kW. If T6-T7 carries 300kW, then T7-T8 must carry 200 kW, which is not possible.
T7-T8 must carry 300 kW and T6-T7 must carry 400 kW. T3-T6 should carry 400 kW more than the requirement at T6.
T6's requirement must equal that of T6-T7.
Requirement at T6 = 400
T3-T6 = 800
The flow in T4-T8 must be equal to the requirement at T4, and each of them must be equal to 100. Therefore, the requirement at T8 = 100 + 300 = 400.
Considering T5, the flow in T5-T1 must be equal to the requirement at T5, i.e. 100, and the flow in T5-T2 must be 100 + 100 + 200 = 400 (balancing the flows at T5).
Now balancing the flows at T1, T1-T2 must be equal to the requirement at T2, i.e. 300.
Now, to meet the conditions at transformer T2, the flow in exactly one out of PP-T2 and T3-T2 must be equal to the requirement at T2, i.e. 200, and the other must be 100.
Now considering T3, the maximum capacity of PP-T3 is 1000.
T3 cannot be more than 100, as then, PP-T3 will be more than 1000.
T3 must be 100 and T3-T2 must be 100.
PP-T3 is 1000.
Hence, the final diagram will be as below:
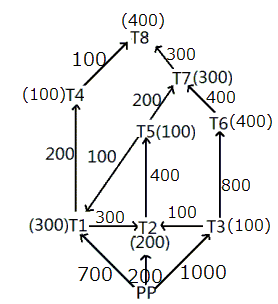
Thus, T8 requires 400 kW of power.
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
Given below is a network of high tension wires from power plant (PP) and 8 transformers T1 to T8. The requirement of power by transformer is exactly met by the electric power provided by the power plant. The electric power in some of the high tension wires and the requirement at some of the transformers has also been mentioned. PP is the source transformer, i.e. the PP does not have any requirement of its own, but it supplies the requirements of all the other transformers.(All values shown in the figure are in KW.)
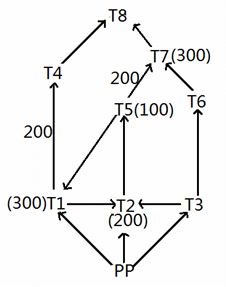
It is also known that:
i. The maximum capacity of any high tension wire is 1000 KW.
ii. The requirement at any transformer, except the power plant and T8, is equal to the flow in exactly one of the high tension wires directly connected to it.
iii. No two high tension wires, directly connected to the same transformer, carry the same amount of electric power.
iv. The flow in none of the high tension wires shown above is zero.
What is the amount of electric power (in kW) carried by the high tension wire T3-T6?
Explanation
As no two high tension wires connecting the same place are carrying same amount of electric power, and at least one of the high tension wires should carry same as that of the place, either T7-T8 or T6-T7 must carry 300 kW. If T6-T7 carries 300kW, then T7-T8 must carry 200 kW, which is not possible.
T7-T8 must carry 300 kW and T6-T7 must carry 400 kW. T3-T6 should carry 400 kW more than the requirement at T6.
T6's requirement must equal that of T6-T7.
Requirement at T6 = 400
T3-T6 = 800
The flow in T4-T8 must be equal to the requirement at T4, and each of them must be equal to 100. Therefore, the requirement at T8 = 100 + 300 = 400.
Considering T5, the flow in T5-T1 must be equal to the requirement at T5, i.e. 100, and the flow in T5-T2 must be 100 + 100 + 200 = 400 (balancing the flows at T5).
Now balancing the flows at T1, T1-T2 must be equal to the requirement at T2, i.e. 300.
Now, to meet the conditions at transformer T2, the flow in exactly one out of PP-T2 and T3-T2 must be equal to the requirement at T2, i.e. 200, and the other must be 100.
Now considering T3, the maximum capacity of PP-T3 is 1000.
T3 cannot be more than 100, as then, PP-T3 will be more than 1000.
T3 must be 100 and T3-T2 must be 100.
PP-T3 is 1000.
Hence, the final diagram will be as below:
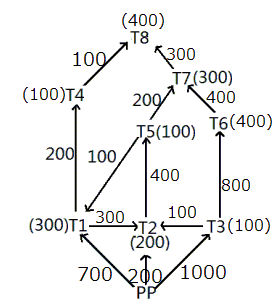
Hence, electric power carried by the high tension wire T3-T6 is 800 kW.
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
Given below is a network of high tension wires from power plant (PP) and 8 transformers T1 to T8. The requirement of power by transformer is exactly met by the electric power provided by the power plant. The electric power in some of the high tension wires and the requirement at some of the transformers has also been mentioned. PP is the source transformer, i.e. the PP does not have any requirement of its own, but it supplies the requirements of all the other transformers.(All values shown in the figure are in KW.)
It is also known that:
i. The maximum capacity of any high tension wire is 1000 KW.
ii. The requirement at any transformer, except the power plant and T8, is equal to the flow in exactly one of the high tension wires directly connected to it.
iii. No two high tension wires, directly connected to the same transformer, carry the same amount of electric power.
iv. The flow in none of the high tension wires shown above is zero.
What is the total requirement of power(in kW) that should be supplied by the power plant?
Explanation
As no two high tension wires connecting the same place are carrying same amount of electric power, and at least one of the high tension wires should carry same as that of the place, either T7-T8 or T6-T7 must carry 300 kW. If T6-T7 carries 300kW, then T7-T8 must carry 200 kW, which is not possible.
T7-T8 must carry 300 kW and T6-T7 must carry 400 kW. T3-T6 should carry 400 kW more than the requirement at T6.
T6's requirement must equal that of T6-T7.
Requirement at T6 = 400
T3-T6 = 800
The flow in T4-T8 must be equal to the requirement at T4, and each of them must be equal to 100. Therefore, the requirement at T8 = 100 + 300 = 400.
Considering T5, the flow in T5-T1 must be equal to the requirement at T5, i.e. 100, and the flow in T5-T2 must be 100 + 100 + 200 = 400 (balancing the flows at T5).
Now balancing the flows at T1, T1-T2 must be equal to the requirement at T2, i.e. 300.
Now, to meet the conditions at transformer T2, the flow in exactly one out of PP-T2 and T3-T2 must be equal to the requirement at T2, i.e. 200, and the other must be 100.
Now considering T3, the maximum capacity of PP-T3 is 1000.
T3 cannot be more than 100, as then, PP-T3 will be more than 1000.
T3 must be 100 and T3-T2 must be 100.
PP-T3 is 1000.
Hence, the final diagram will be as below:
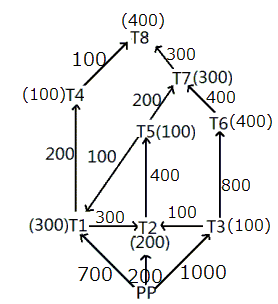
Supply by the power plant should be 1900 KW.
Report a problem
Question for Practice Questions Level 3: Critical Path
Try yourself:Directions: Read the given information carefully and answer the question that follows.
Given below is a network of high tension wires from power plant (PP) and 8 transformers T1 to T8. The requirement of power by transformer is exactly met by the electric power provided by the power plant. The electric power in some of the high tension wires and the requirement at some of the transformers has also been mentioned. PP is the source transformer, i.e. the PP does not have any requirement of its own, but it supplies the requirements of all the other transformers.(All values shown in the figure are in KW.)
It is also known that:
i. The maximum capacity of any high tension wire is 1000 KW.
ii. The requirement at any transformer, except the power plant and T8, is equal to the flow in exactly one of the high tension wires directly connected to it.
iii. No two high tension wires, directly connected to the same transformer, carry the same amount of electric power.
iv. The flow in none of the high tension wires shown above is zero.
What is the amount of electric power (in kW) carried by the high tension wire T2-T5?
Explanation
As no two high tension wires connecting the same place are carrying same amount of electric power, and at least one of the high tension wires should carry same as that of the place, either T7-T8 or T6-T7 must carry 300 kW. If T6-T7 carries 300kW, then T7-T8 must carry 200 kW, which is not possible.
T7-T8 must carry 300 kW and T6-T7 must carry 400 kW. T3-T6 should carry 400 kW more than the requirement at T6.
T6's requirement must equal that of T6-T7.
Requirement at T6 = 400
T3-T6 = 800
The flow in T4-T8 must be equal to the requirement at T4, and each of them must be equal to 100. Therefore, the requirement at T8 = 100 + 300 = 400.
Considering T5, the flow in T5-T1 must be equal to the requirement at T5, i.e. 100, and the flow in T5-T2 must be 100 + 100 + 200 = 400 (balancing the flows at T5).
Now balancing the flows at T1, T1-T2 must be equal to the requirement at T2, i.e. 300.
Now, to meet the conditions at transformer T2, the flow in exactly one out of PP-T2 and T3-T2 must be equal to the requirement at T2, i.e. 200, and the other must be 100.
Now considering T3, the maximum capacity of PP-T3 is 1000.
T3 cannot be more than 100, as then, PP-T3 will be more than 1000.
T3 must be 100 and T3-T2 must be 100.
PP-T3 is 1000.
Hence, the final diagram will be as below:

Hence, 400 kW is carried by the high tension wire T2-T5.
Report a problem






















































