This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Inequalities (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Inequalities
Try yourself:The total money that Vijay (V) and Manju (M) have is less than Rs. 5 but both are having some money. Which of the following is not necessarily true?
Explanation
Total money with Vijay and Manju is less than Rs. 5.
If Vijay is near to 0, then Manju is near to 5.
If Manju is near to 0, then Vijay is near to 5.
Option (1):
3V + 4M < 24
Let V = 1, then M < 5
3 × 1 + 4 × 4 < 24 [True]
Option (2):
3V + 4M < 18
3 + 16 < 18 [False]
Report a problem
Question for Practice Questions Level 3: Inequalities
Try yourself:How many ordered pairs of natural numbers satisfy the inequality 8x + 2y ≤ 24?
Explanation
x = 1, 2y ≤ 16 ⇒ y ∈ [1, 2, 3, 4, 5, 6, 7, 8] ⇒ 8 pairs
x = 2, 2y ≤ 8 ⇒ y ∈ [1, 2, 3, 4] ⇒ 4 pairs
x = 3, y = 0 ⇒ 0 pair
So, a total of 12 pairs are there.
Report a problem
Question for Practice Questions Level 3: Inequalities
Try yourself:If b > a and c < 0, then which of the following is true (a, b > 0)?
Explanation
Report a problem
Question for Practice Questions Level 3: Inequalities
Try yourself:If -1 ≤ v ≤ 1, -2 ≤ u ≤ -0.5, -2 ≤ z ≤ -0.5 and w = vz/u, then which of the following is necessarily true?
Explanation
u is always negative; hence, for us to have a minimum value of vz/u , vz should be positive.
Also, for the least value, the numerator has to be the maximum positive value and the denominator has to be the smallest negative value. In other words, vz has to be 2 and u has to be -0.5.
Hence, minimum value of vz/u = 2/-0.5 = -4
For us to get the maximum value, vz has to be the smallest negative value and u has to be the highest negative value.
Thus, vz has to be -2 and u has to be -0.5.
Hence, maximum value of vz/u = -2/-0.5 = 4
Report a problem
Question for Practice Questions Level 3: Inequalities
Try yourself:If - 2 ≤ a ≤ - 1, - 4 ≤ b ≤ - 2, 2 ≤ c ≤ 4 and 1 ≤ d ≤ 3, what is the maximum value of ab2/cd2 ?
Explanation
Since a is always negative and b2, c and d2 are always positive. So ab2/cd2 is always negative.
So, the maximum value is negative of minimum magnitude.
So, a and b2 should be minimum in magnitude and c and d2 should be maximum.
So, take a = -1, b = 2 and c = 4 and d = 3.
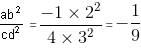
So, maximum value = 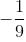
Report a problem
Question for Practice Questions Level 3: Inequalities
Try yourself:For the given consecutive integers p, q, r and s, such that, p, q, r, s > 0, then, which of the following can be true?
Explanation
Consider p = 1, q = 2, r = 3, s = 4
Case 1: p + q < r + s
which implies, 3 < 7, which holds the inequality.
Case 2: (p + q) (rs) = 36
pq (r + s) = 14
36 is not less than 14
Hence, the second option is incorrect
Case 3: (p + q) (r + s) = 21
pq + rs = 14
Hence, option 3 is incorrect.
Report a problem
Question for Practice Questions Level 3: Inequalities
Try yourself:Which of the following is the possible value of a in the given inequality |2a + 3| > |7a - 2|?
Explanation
If 7a - 2 ≥ 0, then, 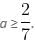
If 2a + 3 ≥ 0, then 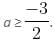
So, three different intervals of a are possible.
Case 1:
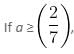 then inequality becomes,
then inequality becomes,
2a + 3 > 7a - 2
5 > 5a
1 > a
So, for case 1,
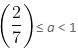
Case 2:
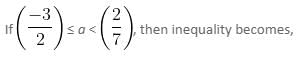
2a + 3 > 2 - 7a
9a > - 1
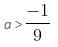
So, for case 2,
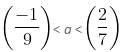
Case 3:
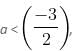 then inequality becomes,
then inequality becomes,
-2a - 3 > 2 - 7a
5a > 5
a > 1, which is not possible as the given inequality is formed only if
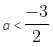
So, combining case 1 and case 2,
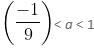 is the correct interval of a.
is the correct interval of a.
Report a problem
Question for Practice Questions Level 3: Inequalities
Try yourself:To determine their favourite brand of chocolates in a particular community, a big chain of retail stores conducted a survey for elementary school kids. In the survey, a kid was presented with a tray of 8 chocolates of different brands and asked to pick one. In all, 400 kids were involved in the survey. Out of the first 100, 20 chose brand C. In the next 200, 40 chose brand C. k kids in the last 100 opted for brand C. If not more than 25% of kids chose brand C, then which of the following inequalities best describes the value for k?
Explanation
Total number of kids surveyed = 100 + 200 + 100 = 400
25% of 400 = 100
Number of kids who chose brand C = 20 + 40 + k = 60 + k
Not more than 25% of the kids chose brand C.
This implies that at the most, 25% of the kids chose brand C.
Thus, at the most, 100 kids chose brand C.
Thus, 60 + k ≤ 100
Or, k ≤ 40
Hence, answer option (3) is correct.
Report a problem
Question for Practice Questions Level 3: Inequalities
Try yourself:For the given pair (x, y) of positive integers, 7x + 3y = 123. How many integral pairs of x and y satisfy the given condition?
Explanation
For the first pair, use the equation, remainder of (7/3)x = remainder of (123/3).
Thus, the first pair is (0, 41). Since only positive integers are permitted, we reject this pair.
But the other pairs can be derived from the above pair.
Now, every third value of x after 0 will give an integral value of y i.e. for x = 3, 6, 9, 12, 15, 18.. and so on, we get integral values of y as 34, 27, 20, 13, 6, - 1,……. and so on.
Thus, only five pairs satisfy our condition: (3, 34), (6, 27), (9, 20), (12, 13) and (15, 6).
Report a problem
Question for Practice Questions Level 3: Inequalities
Try yourself:x and y are real numbers satisfying the conditions 2 < x < 3 and - 8 < y < - 7. Which of the following expressions will have the least value?
Explanation
2 < x < 3 and -8 < y < -7
Since, the value of xy2 is also positive and the least value of x + y is -8 + 2 = -6 ....(i)
And since 2 < x < 3,
⇒ 4 < x2 < 9
And - 8 < y < -7
⇒ 4y < x2y < 9y
⇒ -63 < x2y < -32 ....(ii)
While -105 < 5xy < -80 ....(iii)
Hence, from (i), (ii) and (iii), 5xy is the least because xy2 is positive.
Report a problem

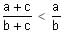
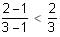
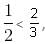 which is true.
which is true.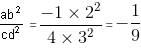
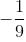
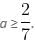
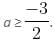
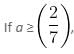 then inequality becomes,
then inequality becomes,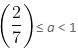
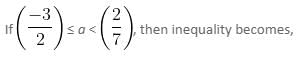
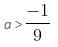
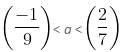
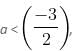 then inequality becomes,
then inequality becomes,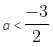
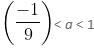 is the correct interval of a.
is the correct interval of a.











