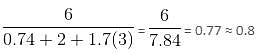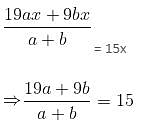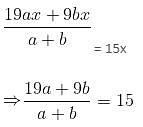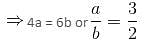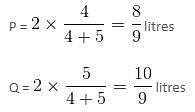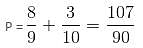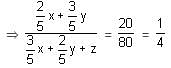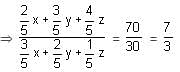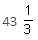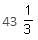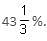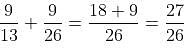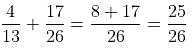This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Mixtures & Alligations (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Mixtures & Alligations
Try yourself:Directions: Read the information given below and answer the question.
Sweetness of various items relative to sucrose, whose sweetness is taken as 1, is:
Lactose: 0.16, Maltose: 0.32, Glucose: 0.74, Sucrose: 1.00, Fructose: 1.70, Saccharin: 675.00
Approximately how many times is sucrose sweeter than a mixture consisting of glucose, sucrose and fructose in the ratio 1 : 2 : 3?
Explanation
Ratio given = 1 : 2 : 3
Sum of the parts of Ratios = 1 + 2 + 3 = 6
Required sweetness = 
Report a problem
Question for Practice Questions Level 3: Mixtures & Alligations
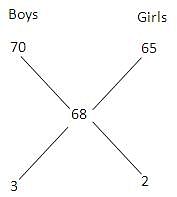
Try yourself:A total of 750 candidates appeared in an examination. 70% of the boys and 65% of the girls passed the examination. If the total pass percentage was 68%, find the number of boys who appeared in the examination.
Explanation
Applying the rule of alligation:

Hence, number of boys who appeared in the examination = 750 × 3/5 = 450
Report a problem
Question for Practice Questions Level 3: Mixtures & Alligations
Try yourself:Gold is 19 times as heavy as water and copper is 9 times as heavy as water. In what respective ratio should these metals be mixed, so that the mixture is 15 times as heavy as water?
Explanation
Report a problem
Question for Practice Questions Level 3: Mixtures & Alligations
Try yourself:Mixtures A and B are contained in two separate vessels. Mixture A contains ingredients P, Q and R in a ratio of 3 : 5 : 2 and mixture B contains ingredients P and Q in a ratio of 4 : 5. We have to make 540 litres of a new mixture by adding the mixtures A and B in a ratio of 1 : 2. What will be the quantity of ingredient P in the final mixture?
Explanation
Report a problem
Question for Practice Questions Level 3: Mixtures & Alligations
Try yourself:The weights of two boxes A and B containing sugar are in the ratio 4 : 5. Some amount of sugar is added to both the boxes and it is found that the weight of box A increases by 10% and the total weight of boxes A and B together becomes 82.8 kg. If this weight is 15% more than the previous weight, then find the percentage with which the weight of box B increases.
Explanation
By alligation method:


x - 15 = 4
x = 19
Report a problem
Question for Practice Questions Level 3: Mixtures & Alligations
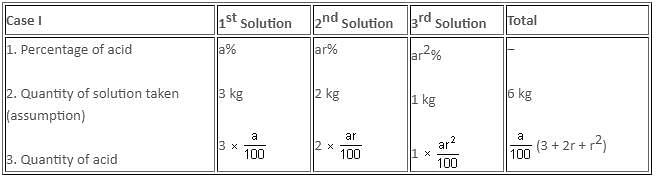
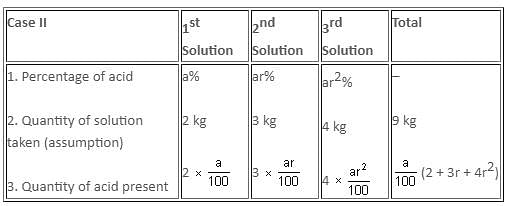
Try yourself:The percentage amounts of an acid in three solutions form a geometric progression. If we mix the first, second and third solutions in the ratio 3 : 2 : 1 by weight, we get a solution containing 22% acid. On the other hand, if we mix the solutions in the ratio 2 : 3 : 4 by weight, we obtain a solution containing 32% acid. Find the percentage of acid in each solution.
Explanation
The given problem is summarised as follows:

That is, 6 kg of solution contains (a/100) x (3 + 2r + r2) kg of acid.
% of acid in this case = ((a/100) x (3 + 2r + r2) x 100)/6 = a/6(3 + 2r + r2)
It is however given that
(a/6) x (3 + 2r + r2) = 22
a x (3 + 2r + r2) = 22 x 6 ... (1)
Now, let us consider the second case where the ratio is 2 : 3 : 4.

9 kg of mixture contains (a/100) x (2 + 3r + 4r2) kg of acid.
% of acid in this case = ((a/100) x (2 + 3r + 4r2) 100)/9 = (a/9) (2 + 3r + 4r2)
This is equal to 32.
Or (a/9) x (2 + 3r + 4r2) = 32
a x (2 + 3r + 4r2) = 32 9 … (2)
Dividing (2) by (1), we get
(a(2 + 3r + 4r2))/(a(3 + 2r + r2)) = (9 x 32)/(6 x 22) = 24/11
4r2 – 3r – 10 = 0
i.e. (r – 2) (4r + 5) = 0
r = 2 or – 5/4
Since –5/4 is inadmissible, r = 2.
Substituting this value in (1) or (2), we get a = 12.
Hence, the percentages are 12%, 24% and 48%.
Report a problem
Question for Practice Questions Level 3: Mixtures & Alligations
Try yourself:There are two solutions of HCl in water. The first is 40% strong and the second is 60% strong. The two solutions are mixed. Some amount of pure water is added and a 20% strong solution is obtained. If instead of adding pure water, the same amount of an 80% strong solution had been added to the mixture, then a 70% strong solution would have been obtained. What was the initial quantity of the 40% and the 60% solutions?
Explanation
Mixture = HCl : Water
Quantity taken out
First 40% = (2 : 3)x kg
Second 60% = (3 : 2)y kg
Let us suppose, we add z kg of water.
When we mixed, we get 20% strong solution.

⇒ 5x + 10y - 5z = 0
x + 2y - z = 0 .......(1)
Again, on adding z kg of 80% solution, we get a 70% solution.

⇒ 15x + 5y - 5z = 0
3x + y - z = 0 ……..(2)
Since variables are more and equations are less, required solution cannot be determined.
Report a problem
Question for Practice Questions Level 3: Mixtures & Alligations
Try yourself:There are three mixtures. The first mixture contains 30% salt and 70% pepper, the second contains 10% pepper and 90% chilly, and the third contains 15% salt, 60% chilly and the rest pepper. They are mixed to obtain a new mixture which contains 40% chilly. The percentage of pepper in the new mixture cannot be more than
Explanation
Report a problem
Question for Practice Questions Level 3: Mixtures & Alligations
Try yourself:There are two qualities of gold alloys 22 carat and 23 carat having different prices per gram, their volumes being 130 gm and 180 gm, respectively. After equal quantities were taken from both the alloys, the alloy removed from the 22-carat alloy was added to the 23-carat alloy and vice versa. The resulting two types of alloys now have the same price per gram. Find the quantity of alloy drawn out from each type. It is to be assumed that 100% gold is 24 carats.
Explanation
Let g grams be removed from each alloy.
As the price of the resulting alloy is the same for both, suppose p% alloy was taken from both alloys.
Quantity of gold metal in the first alloy after interchanging (in gm) = ((22/24) x 130 - (22/24) x g + (23/24) x g) = (p/100) x 130 ... (i)
Or, p/100 = ((22/24) x 130 - (22/24) x g + (23/24) x g)/130 ... (ii)
Similarly, on working for the second alloy, we get
p/100 = ((23/24) x 180 - (23/24) x g + (22/24) x g)/180 ... (iii)
On equating the RHS of (ii) and (iii), we get
((22/24) x 130 - (22/24) x g + (23/24) x g)/130 = ((23/24) x 180 - (23/24) x g + (22/24) x g)/180
18(2860 + g) = 13(4140 - g)
51,480 + 18g = 53,820 - 13g
31g = 2340
g = 75.48
Thus, 75.48 gm is drawn out from each type of alloy.
Thus, answer option b is correct.
Report a problem
Question for Practice Questions Level 3: Mixtures & Alligations
Try yourself:P and Q are two different mouth fresheners, prepared by mixing supari and saunf in the proportions 9 : 4 and 9 : 17, respectively. If equal quantities of the mouth fresheners are mixed to form a third kind of mouth freshener R, find the ratio of saunf to supari in R.
Explanation
In mouth freshener P, quantity of supari = 9/13 qnd quantity of saunf = 4/13
In mouth freshener Q, quantity of supari = 9/26 and quantity of saunf = 17/26
When we add these two mouth fresheners, total quantity of supari = 
Total quantity of saunf =
So, ratio of saunf to supari in R = 25 : 27
Report a problem