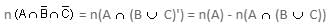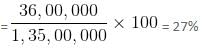This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Set Theory (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Set Theory - 1
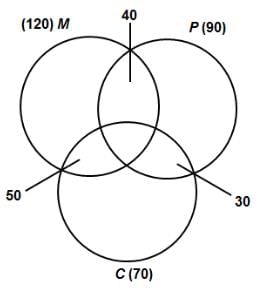
Try yourself:In a survey of 200 students of a higher secondary school, it was found that 120 studied Mathematics, 90 studied Physics, 70 studied Chemistry, 40 studied Mathematics and Physics, 30 studied Physics and Chemistry, 50 studied Chemistry and Mathematics and 20 studied none of these subjects. Find the number of students who studied all the three subjects.
Explanation
Total number of students studying one of the three subjects = 200 - 20
i.e. n(M ∪ P ∪ C) = 180
Now, n(M ∪ P ∪ C) = n(M) + n(P) + n(C) - n(M ∩ P) - n(P ∩ C) - n(M ∩ C) + n(M ∩ P ∩ C)
∴ 180 = 120 + 90 + 70 - 40 - 30 - 50 + n(M ∩ P ∩ C)
∴ n(M ∩ P ∩ C) = 20
Report a problem
Question for Practice Questions Level 3: Set Theory - 1
Try yourself:In a survey conducted among 60 managers, it was found that 25 read Business India, 30 read Business World and 24 read Business Today; 10 read both Business India and Business World, 9 read both Business India and Business Today and 12 read both Business World and Business Today. If 5 managers read all three newspapers, then how many managers read only one newspaper?
Explanation
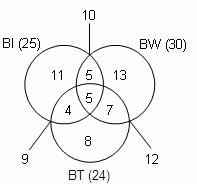
Let BI, BW and BT represent the readers of the three newspapers Business India, Business World and Business Today, respectively.
Now, 5 read all three, so let us put 5 at the centre.
Since 10 read both BI and BW, we shall put 5 more in BI ∩ BW.
BW ∩ BT = 12 = 5 + 7. So, put 7 more in BT ∩ BW.
BI ∩ BT = 9 = 5 + 4, so put 4 more in BT ∩ BI.
Since we know that 25 read BI, only 25 - (5 + 5 + 4) = 11 read BI alone.
Similarly, only 13 read BW alone and only 8 read BT alone.
The required number = 11 + 13 + 8 = 32
Report a problem
Question for Practice Questions Level 3: Set Theory - 1
Try yourself:In a class of 33 students, 20 play cricket, 25 play football and 18 play volleyball. 15 play both cricket and football, 12 play both football and volleyball and 10 play both cricket and volleyball. If each student plays at least one game, find the number of students who play only cricket.
Explanation
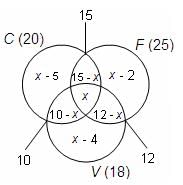
Let C, F and V denote the sets of number of students who play cricket, football and volleyball, respectively.
n(C) = 20, n(F) = 25 and n(V) = 18
n(C ∩ F) = 15, n(F ∩ V) = 12, n(C ∩ V) = 10
Let 'x' be the number of students who play all the 3 games.
Number of students who play both cricket and football, but not volleyball = (15 - x)
Similarly, number of students who play both football and volleyball, but not cricket = (12 - x)
Number of students who play both cricket and volleyball, but not football = (10 - x)
Now, we can find the number of students who play cricket only, football only and volleyball only as follows:
n(C) only = 20 - (15 - x + x + 10 - x) = x - 5
n(V) only = 18 - (10 - x + x + 12 - x) = x - 4
And n(F) only = 25 - (15 - x + x + 12 - x) = x - 2
33 = (x - 5) + (15 - x) + x + (10 - x) + (12 - x) + (x - 4) + (x - 2)
33 = x + 26
x = 7
Number of students who play only cricket = 7 - 5 = 2
Report a problem
Question for Practice Questions Level 3: Set Theory - 1
Try yourself:In a class of 33 students, 20 play cricket, 25 play football and 18 play volleyball. 15 play both cricket and football, 12 play both football and volleyball and 10 play both cricket and volleyball. If each student plays at least one game, then find the number of students who play any two games.
Explanation
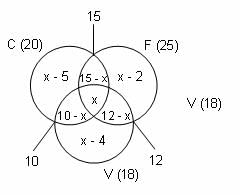
Let C, F and V denote the sets of number of students who play cricket, football and volleyball, respectively.
n(C) = 20, n(F) = 25 and n(V) = 18
n(C ∩ F) = 15, n(F ∩ V) = 12 and n(C ∩ V) = 10
Let 'x' be the number of students who play all the 3 games.
The number of students who play cricket and football, but not volleyball = (15 – x)
Similarly, the number of students who play football and volleyball, but not cricket = (12 – x)
The number of students who play cricket and volleyball, but not football = (10 – x)
Now, we can find the number of students who play cricket only, football only and volleyball only.
n(C) only = 20 – (15 – x + x + 10 – x) = x – 5
n(V) only = 18 – (10 – x + x + 12 – x) = x – 4
n(F) only = 25 – (15 – x + x + 12 – x) = x – 2
33 = (x – 5) + 15 – x + x + 10 – x + 12 – x + x – 4 + x – 2
33 = x + 26
x = 7
Number of students who play any 2 games = Total - [Students who play all 3 games + Students who play only 1 game]
= 33 - [7 + 2 + 5 + 3] = 33 - 17 = 16
Report a problem
Question for Practice Questions Level 3: Set Theory - 1
Try yourself:Directions: Study the given information and answer the following question.
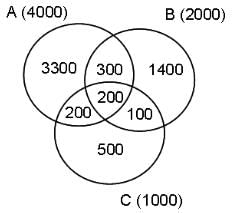
In a survey of 500 customers, the numbers of customers who buy different grades of rice are given below:
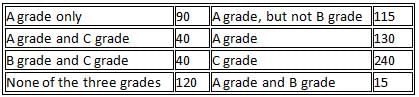
The ratio of frequency of 'B only' to that of 'Both A and C, but not B' is
Explanation
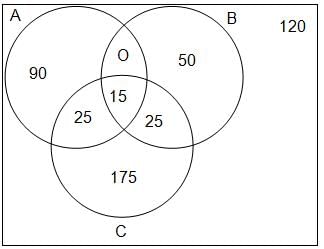
B only = 50
Both A and C, but not B = 25
Required ratio = 50 : 25 = 2 : 1
Report a problem
Question for Practice Questions Level 3: Set Theory - 1
Try yourself:In a town of 10000 families, it was found that 40% families buy newspaper A, 20% families buy newspaper B and 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers, then the number of families that buy A only is
Explanation
Let A, B and C denote the sets of families buying newspapers A, B and C, respectively.
n(A) = 4000, n(B) = 2000 and n(C) = 1000
Also, n(A ∩ B) = 500, n(B ∩ C) = 300 and n(C ∩ A) = 400
n(A ∩ B ∩ C) = 200
Number of families who buy A only = Number of families who buy A - (Number of families who buy A and B, A and C and (A and B and C))
= 4000 - (300 + 200 + 200) = 3300
Alternative method:
We have, N = 10000, n(A) = 40% of 10000 = 4000, n(B) = 2000, n(C) = 1000, n(A ∩ B) = 500, n(B ∩ C) = 300, n(C ∩ A) = 400, n(A ∩ B ∩ C) = 200
We have to find
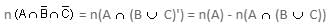
= n(A) - n((A ∩ B) ∪ (A ∩ C))
= n(A) - {n(A ∩ B) + n(A ∩ C) - n(A ∩ B ∩ C)}
= 4000 - (500 + 400 - 200) = 3300
Report a problem
Question for Practice Questions Level 3: Set Theory - 1
Try yourself:Directions: The following question is based on the Venn diagram given below:
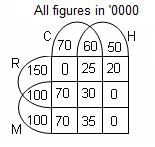
This Venn diagram represents four sets of TV viewers who watch the programmes Mahabharata, Ramayana, Chitrahaar and Hindi films. M, R, C and H respectively represent the number of viewers who watch Mahabharata, Ramayana, Chitrahaar and Hindi films; and M1, R1, C1 and H1 represent respectively the viewers who do not watch them. For example, MR1 and CH1 represent the viewers who watch Mahabharata and Chitrahaar but not Ramayana and Hindi films. (The numbers given are in 10,000).
Q. What is the approximate difference in percentage between people who watch Hindi films and those who watch Chitrahaar? (Assume the TV viewers to be 13.5 million)
Explanation
Percentage of people who watch Chitrahaar
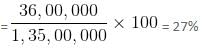
Percentage of people who watch Hindi films

Required difference = 27% - 16% = 11%
Report a problem
Question for Practice Questions Level 3: Set Theory - 1
Try yourself:In a class of 33 students, 20 play cricket, 25 play football, 18 play volleyball, 15 play both cricket and football, 12 play football and volleyball and 10 play cricket and volleyball. If each student plays at least one game, find the number of students who play all the three games.
Explanation
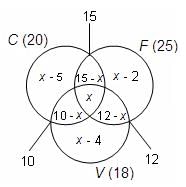
Let C, F and V denote the sets of number of students who play cricket, football and volleyball, respectively.
n(C) = 20, n(F) = 25 and n(V) = 18
n(C ∩ F) = 15, n(F ∩ V) = 12 and n(C ∩ V) = 10
Let 'x' be the number of students who play all the 3 games.
The number of students who play cricket and football, but not volleyball = (15 – x)
Similarly, the number of students who play football and volleyball, but not cricket = (12 – x)
The number of students who play cricket and volleyball, but not football = (10 – x)
Now, we can find the number of students who play cricket only, football only and volleyball only.
n(C) only = 20 – (15 – x + x + 10 – x) = x – 5
n(V) only = 18 – (10 – x + x + 12 – x) = x – 4
n(F) only = 25 – (15 – x + x + 12 – x) = x – 2
33 = (x – 5) + 15 – x + x + 10 – x + 12 – x + x – 4 + x – 2
33 = x + 26
x = 7
The number of students who play all the 3 games = 7
Report a problem
Question for Practice Questions Level 3: Set Theory - 1
Try yourself:In a class of 33 students, 20 play cricket, 25 play football and 18 play volleyball. 15 play both cricket and football, 12 play both football and volleyball and 10 play both cricket and volleyball. If each student plays at least one game, then find the number of students who play only one game.
Explanation
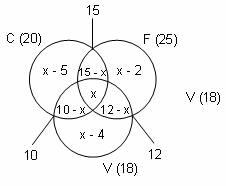
Let C, F and V denote the sets of number of students who play cricket, football and volleyball, respectively.
n(C) = 20, n(F) = 25 and n(V) = 18
n(C ∩ F) = 15, n(F ∩ V) = 12 and n(C ∩ V) = 10
Let 'x' be the number of students who play all the 3 games.
The number of students who play cricket and football, but not volleyball = (15 – x)
Similarly, the number of students who play football and volleyball, but not cricket = (12 – x)
The number of students who play cricket and volleyball, but not football = (10 – x)
Now, we can find the number of students who play cricket only, football only and volleyball only.
n(C) only = 20 – (15 – x + x + 10 – x) = x – 5
n(V) only = 18 – (10 – x + x + 12 – x) = x – 4
n(F) only = 25 – (15 – x + x + 12 – x) = x – 2
33 = (x – 5) + 15 – x + x + 10 – x + 12 – x + x – 4 + x – 2
33 = x + 26
x = 7
Number of students who play only one game = Number who play (C only + V only + F only) = 2 + 3 + 5 = 10
Report a problem
Question for Practice Questions Level 3: Set Theory - 1
Try yourself:Three rugs have a combined area of 200 m2. When partially overlapped, the rugs cover a floor area of 140 m2 and the area covered by exactly two layers of rug is 24 m2. What area of the floor is covered by all three layers of rug?
Explanation
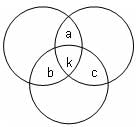
Draw the rugs in the above manner, where a + b + c represents the total area of the floor covered by exactly two rugs and k represents the area of the floor covered by all three rugs. We are told that a + b + c = 24 m2.
Since the total area of the floor covered when the rugs do not overlap is 200 m2 and the total area covered when they do overlap is 140 m2, 60 m2 of rug is either double or triple layered.
Thus, a + b + c + 2k = 60 m2
2k = 36 or k = 18
Thus, the area of the floor covered by all three layers of rug is 18 m2.
Report a problem