This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Time & Work (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Time & Work - 1
Try yourself:A, B and C together can finish a piece of work in 12 days. A and C together work twice as much as B. A and B together work thrice as much as C. In what time will C finish the job alone?
Explanation
Since A and C together work twice as much as B
A + C = 2B ... (1)
And A and B together work thrice as much as C
A + B = 3C ... (2)
Equation (1) - equation (2) gives
C - B = 2B - 3C
Or 3B = 4C
Or B = (4/3)C
Substituting this relation in equation (1), we get
A = (5/3)C
A + B + C = (5/3)C + (4/3)C + C = 4C
This means that 4C can complete the work in 12 days or C can complete in 12 x 4 = 48 days.
Report a problem
Question for Practice Questions Level 3: Time & Work - 1
Try yourself:A, B and C are three pipes attached to a cistern. A and B can fill the cistern respectively in 20 and 30 minutes, while C can empty the cistern in 15 minutes. If A, B and C be kept open successively for 1 minute each, how soon will the cistern be filled?
Explanation
LCM of 15, 20 and 30 is 60.
Let the capacity of tank be 60 liters.
A and B fill the tank at a rate of 3 liters per minute and 2 liters per minute, respectively. C empties the tank at a rate of 4 liters per minute.
If opened successfully for 1 minute each, 1 liter will be filled in 3 minutes.
So, 55 liters will be filled in 55 × 3 = 165 minutes
After the 165th minute, tap A and B will fill the left capacity of 5 liters in 2 minutes.
So, the total time taken = 167 minutes
Report a problem
Question for Practice Questions Level 3: Time & Work - 1
Try yourself:If 10 persons can clean 10 floors in 10 days, in how many days can 8 persons clean 8 floors?
Explanation
10 persons can clean 10 floors in 10 days means 1 person can clean one floor in 10 days
So 8 persons can clean one floor in 10/8 days
8 persons can clean 8 floors in
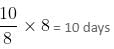
Report a problem
Question for Practice Questions Level 3: Time & Work - 1
Try yourself:A and B can do a piece of work in 6 days. B and C can do the same work in 8 days, and A, B and C together can do it in 4 days. In how many days can A and C do it?
Explanation
Report a problem
Question for Practice Questions Level 3: Time & Work - 1
Try yourself:A man can complete a piece of work in 30 days. If after working for 10 days there is an increase of 25% in his working efficiency, how many days before the scheduled time will he be able to complete the work?
Explanation
After 10 days, he still has to do the work of 20 days.
Since efficiency of the man has increased by 25%, he can do the work in 20 × 100/125 = 16 days.
So, he will complete the work 4 days before the scheduled time.
Report a problem
Question for Practice Questions Level 3: Time & Work - 1
Try yourself:A man can do a piece of work in 60 days. He starts doing the work and on every successive day, he does twice the amount of work done on the previous day. If he goes on at the same rate, in how many days will he be able to complete the work?
Explanation
Let initially, man can do 'x' amount of work in one day.
In 60 days work done = 60x
Man can do 'x' amount of work on the first day. On the second day, he will do 2x, on the third day 4x, and so on.
ATQ,
x + 2x + 4x + 8x + 16x + 32x > 60x
So, he can complete the work on the 6th day.
Report a problem
Question for Practice Questions Level 3: Time & Work - 1
Try yourself:Two pipes individually can fill a tank in 14 hours and 16 hours, respectively. The pipes are opened simultaneously, but by mistake, the outlet pipe at the bottom of the tank was opened as well. Due to this, it took 32 extra minutes for the tank to be filled up. Considering that the tank is full, how much time (in hours) will the outlet pipe take to completely empty a tank double the size?
Explanation
Let the capacity of the tank = LCM of 14 and 16 = 112 L
So, the rates of filling of the two pipes = 112/14 = 8 L/hr and 112/16 = 7 L/hr
So, effective filling rate = 8 + 7 = 15 L/hr
Ideally, time taken to fill the tank

Actual time taken = 32 minutes + 7 hours 28 minutes = 8 hours
Thus, actual filling rate = 112/8 = 14 L/hr
Report a problem
Question for Practice Questions Level 3: Time & Work - 1
Try yourself:A is 25% more efficient than B. With the help of C, B can complete a piece of work in 2/3rd of the time required by A alone. By how much percentage is C less efficient than A?
Explanation
Let the efficiencies of A and B be 5 and 4, respectively.
Let the efficiency of C be x.
Let the time taken by A to finish the work be 3 days.
So, time taken by B and C to finish the work = 2 days
So, total work = 3 × 5 = 15 units
So, (4 + x)2 = 15
Hence, x = 3.5
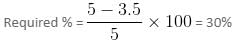
Report a problem
Question for Practice Questions Level 3: Time & Work - 1
Try yourself:A tank has 3 inlet taps, each of which can fill the tank in 20 hours, and 3 outlet taps, each of which can empty the tank in 40 hours. At time t = 0, one inlet tap is opened. After 1 hour, one outlet tap is also opened. Again after one hour, one more inlet tap is opened, and after another hour, one outlet tap is opened and another hour later, one inlet tap is opened. Finally, at the beginning of the sixth hour, all the 6 taps are open and no tap is closed after that until the tank is filled. How much time from the beginning is required for the tank to fill?
Explanation
Report a problem
Question for Practice Questions Level 3: Time & Work - 1
Try yourself:Taps A and B can fill a tank in 10 hours and 30 hours, respectively. Taps C and D can empty the tank in 20 hours and 25 hours, respectively. When the tank is full, both taps C and D are opened for 10 hours and then, both taps C and D are closed and tap A is opened. How much more time does it take to fill the tank completely?
Explanation
Let the volume of the tank be 100v litres.
Let volumetric flow rate through tap A be A litres per hour.
So, 10A = 100v or A = 10v ...(i)
Let volumetric flow rate through tap C be C litres per hour.
So, 20C = 100v or C = 5v ...(ii)
Let volumetric flow rate through tap D be D litres per hour.
So, 25D = 100v or D = 4v ...(iii)
Now, fluid drained through taps C and D in 10 hours = 10(C + D) litres = 10(5v + 4v) litres
= 10(9v) litres = 90v litres
Volume of fluid left to be filled by tap A = 90v litres
Suppose tap A takes t hours to fill the tank.
tA = 90v ...(iv)
Plugging in the value of A in terms of 'v' from equation (i) into equation (iv), we get
t × 10v = 90v
Or, t = 9
Thus, tap A takes 9 hours to full the tank.
Thus, option (2) is correct.
Report a problem

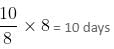
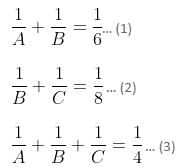
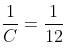
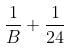

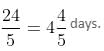

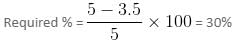
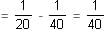
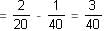
 hours and 20 minutes.
hours and 20 minutes.

















