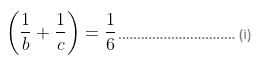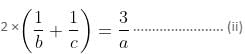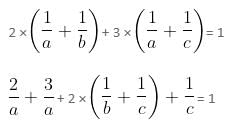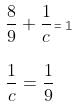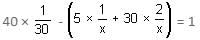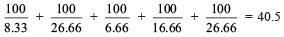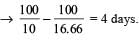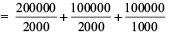This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Time & Work (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Time & Work - 2
Try yourself:A flat of 3 rooms is painted by A, B and C in 5 days. A works for the whole time, B only on the first two days and C only on the last three days. This work could have been done by B and C in 6 days (both working full time) without involving A. If B and C working together can do as much work in two days as A can do in 3 days, then how long will it take for A, B and C, respectively, to do this work alone?
Explanation
Let A, B and C individually take a, b and c days to complete the same task, respectively.
B and C can finish the task in 6 days working together.
Therefore,
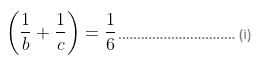
Again, two days of work of B and C equals to 3 days of A's work.
Therefore,
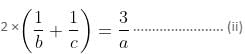
From equation (i),
3/a = 2/6
a = 9 days
Now, A and B work for first two days and A and C work for last three days to complete the same task.
Therefore,
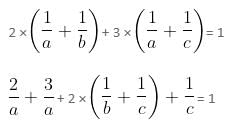
Substitute values of a and from equation (ii).
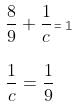
c = 9 days
Substitute values of a and c in equation (i).

b = 18 days
Hence, this is the required solution.
Report a problem
Question for Practice Questions Level 3: Time & Work - 2
Try yourself:An inlet tap can fill a tank in 30 hours. This tap was opened at time zero, but after 5 hours (t = 5), a leak developed at the bottom. After 10 hours (t = 10), the cross section of the leak became double because of which, it took 40 hours to fill the tank. How much time will it take to fill the tank if the cross section of the hole does not change at t = 10?
Explanation
Let the initially formed hole empty the tank in x hours.
After getting the cross section doubled, it empties the tank in x/2 hours.
Inlet tap can fill 1/30th of the tank in 1 hour.
So, in 40 hours,
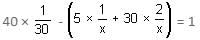
⇒ x = 195 hours
If the cross section of the hole does not change at t = 10,
suppose the tank will fill in t hours.
Report a problem
Question for Practice Questions Level 3: Time & Work - 2
Try yourself:Three pipes A, B and C are attached to a tank. A and B can fill it in 20 and 30 minutes, respectively, while C can empty it in 15 minutes. If A, B and C are kept open successively for 1 minute each, how soon will the tank be filled if pipe A is opened first?
Explanation
The part of tank filled by Pipe A in 1 minute = 1/20
The part of tank filled by Pipe B in 1 minute = 1/30
The part of tank emptied by Pipe C in 1 minute = 1/15
So, totally in 3 minute (because open for 1 minute each) = 1/20 + 1/30 - 1/15 = 1/60
Consider 55/60 can be filled in 3 × 55 = 165 minute, remaining part is 1/12.
A can fill 1/20 in 1 minute.
So, capacity left is, (1/12) - (1/20) = 1/30
B can fill the remaining 1/30 in 1 minute.
So, total time taken = ((3 × 55) + 1 + 1) = 167 minute
Hence, it will take 167 minutes to fill the tank.
Report a problem
Question for Practice Questions Level 3: Time & Work - 2
Try yourself:There are two walls to be built. Area of one wall is twice that of the other. The labourers work on the larger wall for half a day. For the remaining half of the day, half of the labourers work on the larger wall, while the remaining work on the smaller wall. At the end of the day, the larger wall is completely built, while some portion of the smaller wall is left to be built, which is completed by one labourer the next day. How many labourers worked on the first day?
Explanation
Let 4x be the total number of labourers.
4x labourers' work in half a day = 2x labourers' work in one day
Half of 4x, i.e. 2x labourers' work in second half of the day = x labourers' work in one day
According to given information, at the end of the day, the larger wall is completed.
Total 3x labourers are required to work full day to complete the work.
For smaller wall:
2x labourers' work in second half of the day = x labourers' work in one day
But, at the end of the first day, it was not completed and needed one labourer's full-day work.
Therefore, total number of labourers required for smaller wall = x + 1
x + 1 is half of the 3x.
x + 1 = 3x/2
x = 2
Total number of labourers who worked on the first day = 4 × 2 = 8
Report a problem
Question for Practice Questions Level 3: Time & Work - 2
Try yourself:A and B worked together and completed a piece of work in 24 days. They got some money for their work. If they had distributed that money according to their work, A would have received 50% more money than B. In how many days could B alone complete the same work?
Explanation
Let work done by A in 1 day be A, and that done by B in 1 day be B.
Let total work be W.
While working together, A and B took 24 days to complete the work. Therefore, we have
24(A + B) = W ...(i)
Also, as A received 50% more money than B, it is fair enough to assume that A must have done 1.5 times as much work in the same time as B.
Thus, A = 1.5B ...(ii)
Now, plugging the value of A as 1.5B from equation (ii) into equation (i), we have 24(2.5 B) = W or B = W/60 ...(iii)
Suppose, B took d days to do the same work alone.
Thus, dW/60 = W, or d = 60
Thus, working alone, B would take 60 days to do the work.
Hence, answer option (4) is correct.
Report a problem
Question for Practice Questions Level 3: Time & Work - 2
Try yourself:Pipe A fills a tank of 700 litres capacity at the rate of 40 litres/minute. Another pipe B fills the same tank at a rate of 30 litres/minute.Pipe C, which is at the bottom of the tank drains the tank at the rate of 20 litres/minute. Pipe A is kept open for a minute and then closed. Pipe B is kept open for a minute and then closed. Pipe C is kept open for a minute and then closed and the whole cycle is repeated. What minimum time will it take for the given tank to overflow?
Explanation
After 1 minute, 40 litres is filled.
After 2 minutes, another 30 litres is filled (total 70 litres).
After 3 minutes, 20 litres is emptied.
Therefore, at the end of 3 minutes, 50 litres is filled.
50 litres is filled in 3 minutes.
Pipe A fills the tank at the rate of 40 litres a minute.
Pipe B at the rate of 30 litres a minute and Pipe C drains the tank at the rate of 20 litres a minute.
If each of them is kept open for a minute in the order A - B - C, the tank will have 50 litres of water at the end of 3 minutes. After 13 such cycles, the tank will have 13 × 50 = 650 litres of water.
It will take 13 × 3 = 39 minutes for the 13 cycles to be over. At the end of the 39th minute, Pipe C will be closed and Pipe A will be opened. It will add 40 litres to the tank. Therefore, at the end of the 40th minute, the tank will have 650 + 40 = 690 litres of water.
Report a problem
Question for Practice Questions Level 3: Time & Work - 2
Try yourself:Directions: Study the following tables and answers the questions that follow.
Darbar Toy Company has to go through the following stages for the launch of a new toy
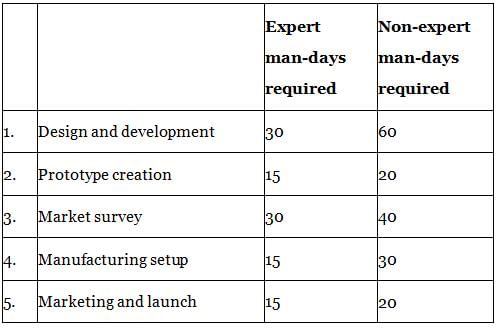
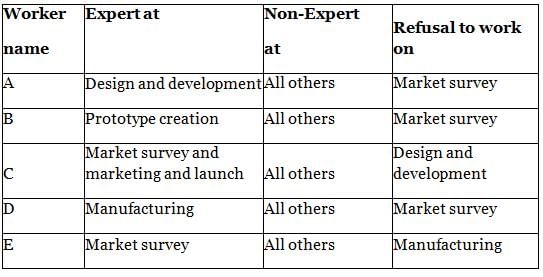
The profile of the company’s manpower is
Q. Given this situation, the minimum number of days in which the company can launch a new toy going through all the stages is
Explanation
Interpretation of the first row of the first table in the question:
Design and Development requires 30 expert man- days or 60 non-expert man-days.
Hence, work done in 1 expert man-day = 3.33% and work done in 1 non-expert man-day = 1.66%. Further, from the second table, it can be interpreted that: A is an expert at design and development. Hence, his work rate is 3.33% per day and B, D and E are ready to work as non-experts on design and development, hence their work rate is 1.66% per day each.
Thus, in 1 day the total work will be
A + B + D + E = 3.33 + 1.66 + 1.66 + 1.66 = 8.33%
work.
Thus, 12 days will be required to finish the design and development phase.
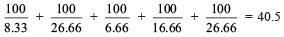
Report a problem
Question for Practice Questions Level 3: Time & Work - 2
Try yourself:Directions: Study the following tables and answers the questions that follow.
Darbar Toy Company has to go through the following stages for the launch of a new toy

The profile of the company’s manpower is

Q. If A and C refuse to have anything to do with the manufacturing set up. The number of days by which the project will get delayed will be
Explanation
Interpretation of the first row of the first table in the question:
Design and Development requires 30 expert man- days or 60 non-expert man-days.
Hence, work done in 1 expert man-day = 3.33% and work done in 1 non-expert man-day = 1.66%. Further, from the second table, it can be interpreted that: A is an expert at design and development. Hence, his work rate is 3.33% per day and B, D and E are ready to work as non-experts on design and development, hence their work rate is 1.66% per day each.
Thus, in 1 day the total work will be
A + B + D + E = 3.33 + 1.66 + 1.66 + 1.66 = 8.33%
work.
Thus, 12 days will be required to finish the design and development phase.
Increase of number of days
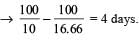
Report a problem
Question for Practice Questions Level 3: Time & Work - 2
Try yourself:Directions : Read the following and answer the questions that follow.
A fort contains a granary, that has 1000 tons of grain. The fort is under a siege from an enemy army that has blocked off all the supply routes.
The army in the fort has three kinds of soldiers:
Sepoys → 2,00,000.
Mantris → 1,00,000
Footies → 1,00,000
100 Sepoys can hold 5% of the enemy for one month. 100
Mantris can hold 10% of the enemy for 15 days. 50
Footies can hold 5% of the enemy for one month.
A sepoy eats 1 kg of food per month, a Mantri eats 0.5 kg of food per month and a footie eats 3 kg of food. (Assume 1 ton = 1000 kg).
The king has to make some decisions based on the longest possible resistance that can be offered to the enemy.
If a king selects a soldier, he will have to feed him for the entire period of the resistance. The king is not obliged to feed a soldier not selected for the resistance.
(Assume that the entire food allocated to a particular soldier for the estimated length of the resistance is redistributed into the king’s palace in case a soldier dies and is not available for the other soldiers.)
Q. If the king strategically attacks the feeder line on the first day of the resistance so that the grain is no longer a constraint, the maximum time for which the resistance can last is
Explanation
For these questions, since food is no longer a constraint, the constraint then becomes the number of lives. Then, the assumption will be that the resistance lasts for one month with a loss of either 2000 sepoys, 2000 mantris or 1000 footies.
Length of resistance
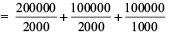
= 250 months.
Report a problem
Question for Practice Questions Level 3: Time & Work - 2
Try yourself:Directions : Read the following and answer the questions that follow.
A fort contains a granary, that has 1000 tons of grain. The fort is under a siege from an enemy army that has blocked off all the supply routes.
The army in the fort has three kinds of soldiers:
Sepoys → 2,00,000.
Mantris → 1,00,000
Footies → 1,00,000
100 Sepoys can hold 5% of the enemy for one month. 100
Mantris can hold 10% of the enemy for 15 days. 50
Footies can hold 5% of the enemy for one month.
A sepoy eats 1 kg of food per month, a Mantri eats 0.5 kg of food per month and a footie eats 3 kg of food. (Assume 1 ton = 1000 kg).
The king has to make some decisions based on the longest possible resistance that can be offered to the enemy.
If a king selects a soldier, he will have to feed him for the entire period of the resistance. The king is not obliged to feed a soldier not selected for the resistance.
(Assume that the entire food allocated to a particular soldier for the estimated length of the resistance is redistributed into the king’s palace in case a soldier dies and is not available for the other soldiers.)
Q. If the feeder line is opened after 6 months and prior to that the king had made decisions based on food availability being a constraint then the number of months (maximum) for which the resistance could last is
Explanation
For these questions, since food is no longer a constraint, the constraint then becomes the number of lives. Then, the assumption will be that the resistance lasts for one month with a loss of either 2000 sepoys, 2000 mantris or 1000 footies.
In 6 months, the resistance will have lost 12000 mantris. He would also have lost all other soldiers since he has not fed them.
Report a problem