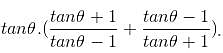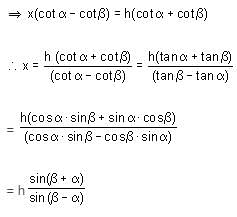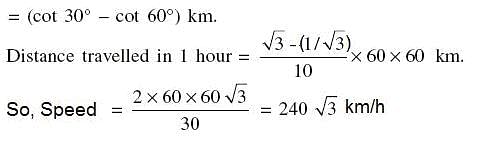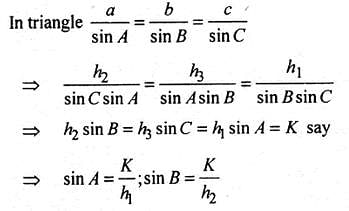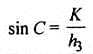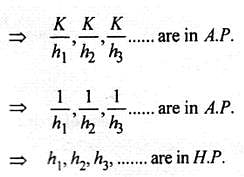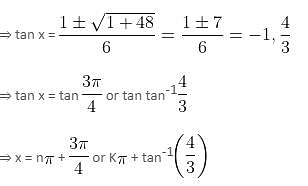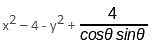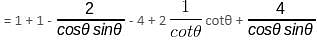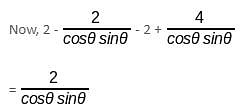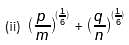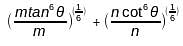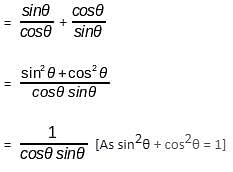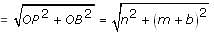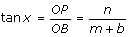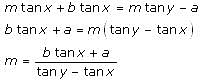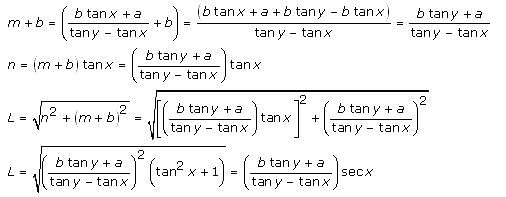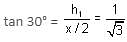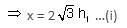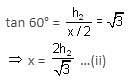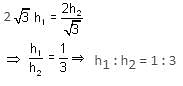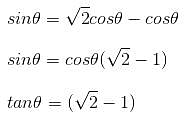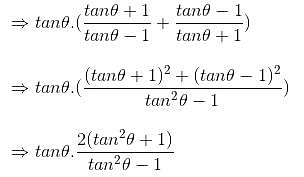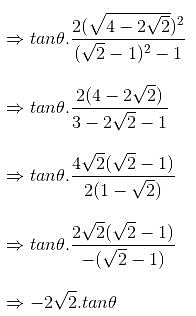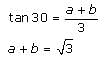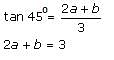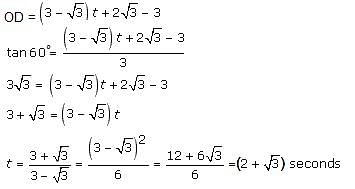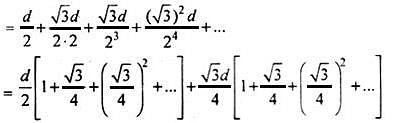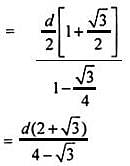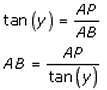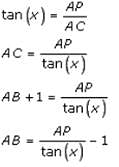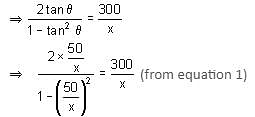This EduRev document offers 15 Multiple Choice Questions (MCQs) from the topic Trigonometry (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Trigonometry
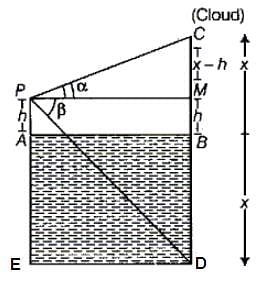
Try yourself:If the angle of elevation of a cloud from a height h above the level of water in a lake is α and the angle of depression of its image is β, then which of the following cannot be the height of the cloud above the level of water in the lake?
Explanation
Let BC = BD = x
∠CPM = α and ∠MPD = β

Also, BM = AP = h
∴ MC = x - h
and DM = x + h
Now, in CPM;
PM = MC cot α = (x - h)cot α …(i)
In ΔDPM;
PM = DM cot β = (x + h) cot β …(ii)
From eq. (i) and (ii), we get:
(x - h) cot α = (x + h) cot β

Report a problem
Question for Practice Questions Level 3: Trigonometry
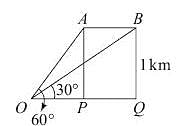
Try yourself:An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. If after 10 seconds, the elevation is observed to be 30°, then the uniform speed of the aeroplane is
Explanation

Distance travelled in 10 sec = AB = PQ = OQ - OP

Report a problem
Question for Practice Questions Level 3: Trigonometry
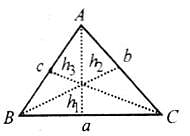
Try yourself:If in a triangle ABC, sin A, sin B and sin C are in AP, then
Explanation
Report a problem
Question for Practice Questions Level 3: Trigonometry
Try yourself:The complete solution of the equation 7 cos2 x + sin x cos x - 3 = 0 is
Explanation
7 cos2x + sin x cos x - 3 = 0
⇒ 7 + tan x - 3 sec2x = 0 (dividing both sides by cos2x)
⇒ 7 + tan x - 3(1 + tan2x) = 0
⇒ 3 tan2x - tan x - 4 = 0

n, K ∈ I
Report a problem
Question for Practice Questions Level 3: Trigonometry
Try yourself:If xcotθ - ycosecθ = a and xcosecθ - ycotθ = b, then (y2 - x2)2 is equal to
Explanation
xcotθ – ycosecθ = a
Squaring both sides, we get
x2cot2θ + y2cosec2θ – 2.xy.cotθ.cosecθ = a2 --- (1)
xcosecθ – ycotθ = b
Squaring both sides, we get
x2cosec2θ + y2cot2θ – 2.xy.cosecθ.cotθ = b2 --- (2)
Subtracting (2) from (1), we get
x2cot2θ + y2cosec2θ – 2.xy.cotθ.cosecθ - (x2cosec2θ + y2cot2θ – 2.xy.cosecθ.cotθ) = a2 - b2
x2cot2θ + y2cosec2θ - x2cosec2θ - y2cot2θ = a2 - b2
cosec2θ(y2 – x2) – cot2θ(y2 – x2) = a2 – b2
(y2 – x2)(cosec2θ – cot2θ) = a2 – b2
(y2 – x2) = a2 – b2
Squaring both sides,
(y2 – x2)2 = (a2 - b2)2
Report a problem
Question for Practice Questions Level 3: Trigonometry
Try yourself:What is the value of q if cot(p + q – r + s) = 0, sin(p – q) = 1/2 , cosec(q + s) = √2 and sec(q + r) = 1?
Explanation
cot(p + q – r + s) = 0
cot(p + q – r + s) = cot 90°
Therefore, (p + q – r + s) = 90° --- (1)
Now, sin(p – q) = 1/2
sin(p – q) = sin 30°
So,(p – q) = 30° --- (2)
Also, cosec(q + s) = √2
cosec(q + s) = cosec 45°
(q + s) = 45° --- (3)
And sec(q + r) = 1
sec(q + r) = sec 0°
(q + r) = 0° --- (4)
Now, adding equations (2) and (4),
p + r = 30° --- (5)
Now, putting (3) in (1),
So, p – r = 90° - 45° = 45° --- (6)
Now, subtracting equation (6) from equation (5),
2r = -15°
r = -7.5°
Now, putting r = -7.5° in equation (4), we get
q = 7.5°
Report a problem
Question for Practice Questions Level 3: Trigonometry
Try yourself:What is the value of x2 - 4 - y2 + 4/(cosθ sinθ) if x = secθ – cosecθ and y = tanθ – cotθ?
Explanation
Report a problem
Question for Practice Questions Level 3: Trigonometry
Try yourself:Fill in the blanks:
(i) If sec4θ + sec2θ = 1, then the value of 3 tan2θ + tan4θ is ____________.
(ii) The value of +, if (p/m)(1/6) + (q/n)(1/6), if p = m tan6θ and q = n cot6θ, is ___________.
(iii) If o = g cosecθ, m = gcotθ and n = Isecθ, then the value of o2 – m2 – n2 + I2tan2θ is ________.
Explanation
Report a problem
Question for Practice Questions Level 3: Trigonometry
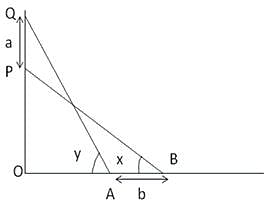
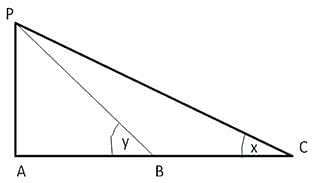
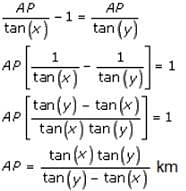
Try yourself:A pole of length 'L', leaning against a wall makes an angle x. When the foot of the pole was moved by a distance of 'b' towards the wall, the top of the pole moves by a distance 'a' upwards and the pole makes an angle y. What is the value of L?
Explanation
Report a problem
Question for Practice Questions Level 3: Trigonometry
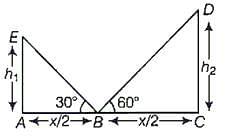
Try yourself:If two towers of heights h1 and h2 subtend angles 30° and 60°, respectively at the mid-point of the line joining their feet, then h1 : h2 is
Explanation
Report a problem
Question for Practice Questions Level 3: Trigonometry
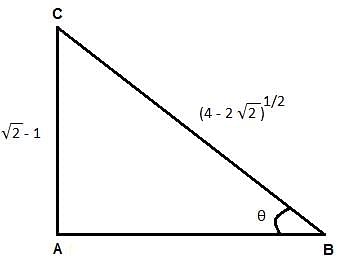
Try yourself:If sinθ + cosθ = √2cosθ, then find the value of

Explanation
Report a problem
Question for Practice Questions Level 3: Trigonometry
Try yourself:A rocket fired vertically moves according to the relation s = at + b, where s is in kilometres and t in seconds. When it was observed from a point on the ground, which is at a distance of 3 km from the point of projection, it was found that at t = 1 second, the angle of elevation was 30° and at t = 2 seconds, the angle of elevation was 45°. Find the time at which the angle of elevation is 60°.
Explanation
Report a problem
Question for Practice Questions Level 3: Trigonometry
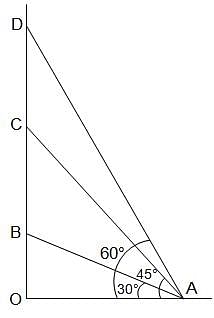
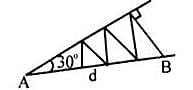
Try yourself:Two rays are drawn from a point making an angle of 30° with each other. A point B is taken on one of them at a distance d from point A. A perpendicular is drawn from point B to the other ray and another perpendicular is drawn from its foot to meet AB at another point from where the similar process is repeated indefinitely. The length of the resulting infinite polygonal line is equal to
Explanation
Report a problem
Question for Practice Questions Level 3: Trigonometry
Try yourself:A person sitting in an aeroplane, which is flying at a certain height, observes the angles of depression of two consecutive milestones lying at a distance of 1 km on the road to be x and y. Determine the height of the aeroplane above the ground.
Explanation
Report a problem
Question for Practice Questions Level 3: Trigonometry
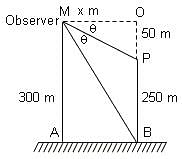
Try yourself:A 50 m high pole stands on a 250 m high building. To an observer at a height of 300 m, the building and the pole subtend equal angles. The distance of the observer from the top of the pole is
Explanation

From the figure, we find that
tan θ = 50/x (From triangle OMP) ... (1)
Also, tan 2θ = 300/x (From triangle OBM) ... (2)

⇒ 3(x2 - 2500) = x2
⇒ x2 = 3x2 - 7500
⇒ 2x2 = 7500
⇒ x2 = 3750 = 625 × 6
⇒ x = 25√6
Hence, distance of the observer from the top of the pole is 25√6m.
Report a problem