Class 9 Maths Chapter 6 Practice Question Answers - Lines and Angles
Q1: Draw a line segment AB of 4 cm in length. Draw a line perpendicular to AB through A and B, respectively. Are these lines parallel?
If true write 1 and if false then write 0
Ans: The lines are perpendicular to a common line AB. Hence, the angle between these lines will be 90∘ + 90∘ = 180∘
Since, the angle between them is 180∘, the lines are parallel to each other.
Q2: Can two acute angles be complement to each other always?
If true, then enter 1 and if false, then enter 0.
Ans: We know, acute angle is the angle which is greater than 0º and less than 90º.
Two acute angles can be complementary to each other but it is not always true.
E.g.: Let us suppose two acute angles are 70º & 30º.
Here, the sum of these two acute angles will give us 100º.
Since, for being complementary, sum should be equal to 90º, we can say that not all pairs of acute angles are complementary.
Hence, the statement is false and 0 is the answer.
Q3: If true then enter 1 and if false then enter 0
Can two obtuse angles be adjacent angles?
Ans: If the sum of 2 angles is less than 360º , then they can be adjacent.
⇒ Since an obtuse angle is less than 180º , the sum of 2 obtuse angles will always be less than 360º.
Hence, two obtuse angles can be adjacent angles.
∴ The answer is 1
Q4: At 4:15, the angle formed between the two hands of a clock is:
(a) acute
(b) obtuse
(c) right angle
(d) none of these
Ans: (a)
At 4:15, the hour will be between 4 and 5.
And minute hand will be on 3.
Thus, the angle formed between these two hands will be less than 90o.
Hence, they form a acute angle.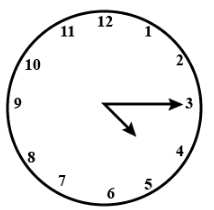
Q5: ∠ABC in the following figure is a / an: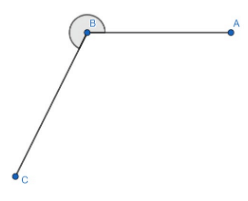 (a) acute angle
(a) acute angle
(b) obtuse angle
(c) reflex angle
(d) straight angle
Ans: (c)
Angles larger than a straight angle but less than complete angle (i.e. between 180º and 360º) are called reflex angles.
Here, the given ∠ABC measures greater than 180º but less than 360º.
Hence, the given angle is a reflex angle.
Therefore, option C is correct.
Q6: Two supplementary angles are in the ratio 4 : 5. The angles are
(a) 90º , 90º
(b) 80º , 100º
(c) 30º , 150º
(d) 45º , 45º
Ans: (b)
Let the angles be 4x and 5x
Angles are supplementary
∴4x + 5x = 180º
⇒ 9x = 180º
⇒ x = 20∘
So the angles ar
4×20º = 80º
5×20º =100º
Q7: The complement of (90º − a) is :
(a) −a
(b) 90º + a
(c) 90º − a
(d) a
Ans: (d)
Let the complement be y.
We know, two angles are complementary if their sum is 90º.
∴ 90º −a + y = 90º
⇒ y = a.
Hence, option D is correct.
Q8: Measure of an angle is given below. Find the measure of it's complementary angle: 58º.
Ans: We know, two angles are complementary when they add up to 90º.
Given, measure of one complementary angle is 58º.
⇒ Measure of other complementary angle =90º −58º = 32º.
Hence, measure of the complementary angle of 58º is 32º.
Q9: Measures of some angles are given below. Find the measures of their supplementary angles.
108º
Ans: Supplementary angles are two angles with a sum of 180º.
One supplement angle is 108º.
⇒ Other supplement angle =180º − 108º = 72º.
∴ Measure of a supplementary angle of 108º = 72º
Q10: Measures of some angles are given below. Find the measure of their complementary angle: 56º
Ans: We know, two angles are said to be complementary, if the sum of their measures is 90º.
The given angle is 56º.
Let the measure of its complement be xº.
Then,
⟹ x + 56º = 90º
⟹ x = 90º − 56º
⟹ x = 34º.
Hence, the complement of the given angle measures 34º.
Q11: In the figure, if OP||RS, ∠OPQ = 110º and∠QRS = 130º , then ∠PQR is equal to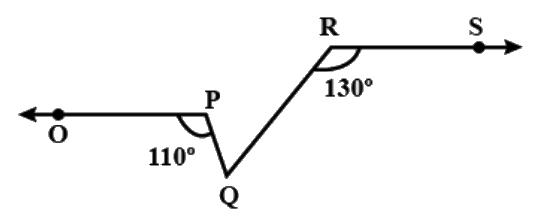 (a) 40º
(a) 40º
(b) 50º
(c) 60º
(d) 70º
Ans: (c)
As OP||RS,
∠ PQR =180−(180−110)−(180−130) = 60
Q12: Find x + y + z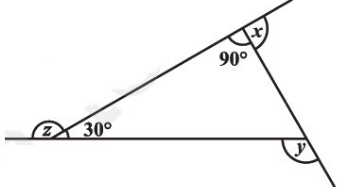 (a) x + y + z = 180º
(a) x + y + z = 180º
(b) x + y + z = 360º
(c) x + y + z = 480º
(d) x + y + z = 540º
Ans: (b)
Here, by exterior angle property, ∠y being an exterior angle, will be the sum of opposite interior angles. Then, ∠y = 90º + 30º = 120º .
We know, by straight angle property, sum of angles on a straight line =180º.
Then, ∠z + 30º =180º
⟹ ∠z = 150º.
Also, ∠x + 90º =180º
⟹ ∠x = 90º.
Therefore, x + y + z = 120º + 150º + 90º = 360º.
Therefore, option B is correct.
Q13: In the given figure, ∠QPB is,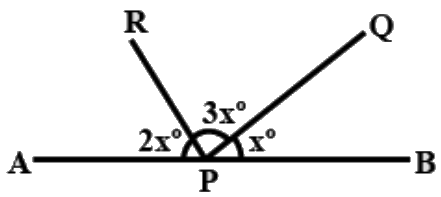 (a) 60º
(a) 60º
(b) 45º
(c) 30º
(d) 15º
Ans: (c)
In the given figure,
∠APR + ∠RPQ + ∠QPB = 180º
2x + 3x + x = 180º
6x = 180º
x = 30º
Q14: If two supplementary angles are in the ratio 2 : 7, then the angles are :
(a) 35º , 145º
(b) 70º , 110º
(c) 40º, 140º
(d) 50º, 130º
Ans: (c)
Hint: Sum of supplementary angles is 180∘
Step1: Evaluate using addition of ratio
Given
ratio = 2:7
Let angles as 2x and 7x
As we know that sum of supplementary angle is 180
⇒ 2x + 7x = 180
⇒ 9x = 180
⇒ x = 20
2x ⇒ 2(20) = 40
7x ⇒ 7(20) = 140
Hence, the angles are 40º140º.
Option C is correct.
Q15: Two angles are called adjacent if
(a) they have a common vertex
(b) they have a ray in common
(c) their other arms lie on the opposite sides of the common arm
(d) all the above
Ans: (d)
We know that, adjacent angles are angles that have a common vertex and a common side, but do not overlap. Also, their other arms lie on the opposite side of the common arm.
So, all the given options are correct.
Hence, option D is the answer.
Q16: In the adjacent figure, BA and BC are produced to meet CD and AD produced in E and F. Then ∠AED + ∠CFD is ________.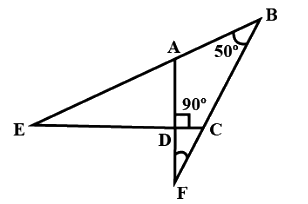 (a) 80o
(a) 80o
(b) 50o
(c) 40o
(d) 160o
Ans: (c)
In △AED,
∠AED+∠EAD+90°=180°
⇒∠AED+∠EAD=90°
⇒∠EAD=90°−∠AED........(i)
Also,
∠EAD=50°+∠AFB.........(ii) (exterior angle property)
From (i) and (ii), we have,
50°+∠AFB=90°−∠AED
⇒∠AFB+∠AED=40°
⇒∠AED+∠CFD=40°(∠AFB=∠CFD).
Therefore, option C is correct.
Q17: In the given figure, magnitude of angles are ..........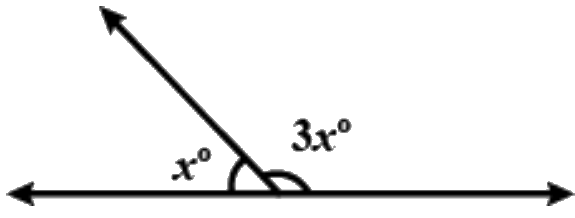 (a) 40º, 120º
(a) 40º, 120º
(b) 30º, 90º
(c) 45º, 135º
(d) 50º, 150º
Ans: (c)
Given: we know that angle constructed by a st line is 180 o
So, xº + 3xº =180º
4xº =180º x = 45º
Hence 3x = 45 × 3 =135º
∴ option C is correct
Q18: Mark the correct alternative of the following.
In figure, if AB∣∣CD, then x=?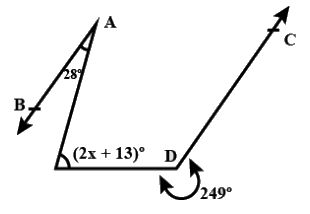 (a) 62
(a) 62
(b) 42
(c) 52
(d) 31
Ans: (b)
Constructions:- Extended AB to F and then F to E and FE to X
obtuse ∠CDE = 249º
∴∠CDE = 360º − 249º = 111º
So, ∠CDX = 180º − ∠CDE = 180º − 111º = 69º =∠AFE (corresponding angles)
∠AED=∠A +∠AFE (exterior angle prop.)
⇒ 2x + 13 = 28 + 69
⇒ 2x = 84 ⇒ x = 42º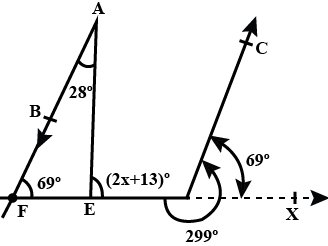
Q19: In figure, AB∣∣CD and AE∣∣CF, ∠FCG = 90º and ∠BAC = 120º. Find the values of x, y and z.
Ans: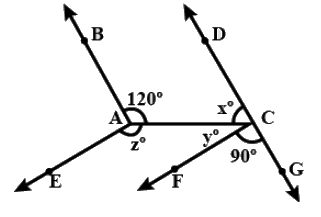 AB∣∣CD and AE∣∣CF, ∠FCG=90º and ∠BAC=120º
AB∣∣CD and AE∣∣CF, ∠FCG=90º and ∠BAC=120º
line AB ∣∣ line CD
∴ ∠BAC and ∠ACD are supplementary angles.
Sum of supplementary angles is 180º
∴∠BAC+∠ACD=180º
∴120 0 +x = 180º
∴ x = 60º
Also, ∠DCA +∠ACF+∠FCG = 180º
x+y+90 0 =180º
60 0 + y + 90º = 180º
y = 30º
line AE ∣∣ line CF
∴ ∠EAC and ∠ACF are supplementary angles.
Sum of supplementary angles is 180º
∴∠EAC + ∠ACF = 180º
∴ z + y = 180º
∴ z + 30 = 180º
∴ z = 150º
Q20: In Fig., ∠AOF and ∠FOG form a linear pair. If ∠EOB = ∠FOC = 90∘ and ∠DOC = ∠AOB = 30º.
Name three pairs of adjacenet angles.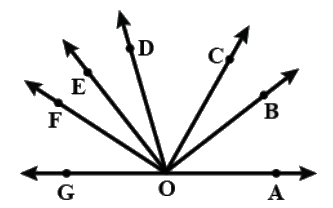 Ans: Adjacent Angles are those angles that share a common side and a common point (vertex) and they shouldn’t overlap
Ans: Adjacent Angles are those angles that share a common side and a common point (vertex) and they shouldn’t overlap
Hence ∠BOC, ∠COD; ∠COD, ∠DOE; ∠DOE, ∠EOF are pairs of adjacent angles.
|
44 videos|412 docs|54 tests
|


















