Class 8 Maths Chapter 3 Practice Question Answers - Understanding Quadrilaterals

Q1: A diagonal and a side of a rhombus are of equal length. Find the measure of the angles of the rhombus.
Sol:
Let ABCD be the rhombus.
Thus, AB = BC = CD = DA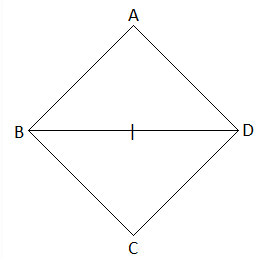

Given that a side and diagonal are equal.
AB = BD (say)
Therefore, AB = BC = CD = DA = BD
Now, all the sides of a triangle ABD are equal.
Therefore, ΔABD is an equilateral triangle.
Similarly,
ΔBCD is also an equilateral triangle.
Thus, ∠A = ∠ABD = ∠ADB = ∠DBC = ∠C = ∠CDB = 60°
∠B = ∠ABD + ∠DBC = 60° + 60° = 120°
And
∠D = ∠ADB + ∠CDB = 60° + 60° = 120°
Hence, the angles of the rhombus are 60°, 120°, 60° and 120°.

Q2: ABCD is a parallelogram with ∠A = 80°. The internal bisectors of ∠B and ∠C meet each other at O. Find the measure of the three angles of ΔBCO.
Sol:
Given,
∠A = 80°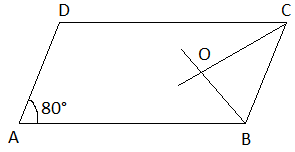

We know that the opposite angles of a parallelogram are equal.
∠A = ∠C = 80°
And
∠OCB = (1/2) × ∠C
= (1/2) × 80°
= 40°
∠B = 180° – ∠A (the sum of interior angles on the same side of the transversal is 180)
= 180° – 80°
= 100°
Also,
∠CBO = (1/2) × ∠B
= (1/2) × 100°
= 50°
By the angle sum property of triangle BCO,
∠BOC + ∠OBC + ∠CBO = 180°
∠BOC = 180° – (∠OBC + CBO)
= 180° – (40° + 50°)
= 180° – 90°
= 90°
Hence, the measure of all the three angles of a triangle BCO is 40°, 50° and 90°.

Q3: Adjacent sides of a rectangle are in the ratio 5 : 12, if the perimeter of the rectangle is 34 cm, find the length of the diagonal.
Sol:
Given,
Ratio of the adjacent sides of the rectangle = 5 : 12
Let 5x and 12x be the two adjacent sides.
We know that the sum of all sides of a rectangle is equal to its perimeter.
Thus,
5x + 12x + 5x + 12x = 34 cm (given)
34x = 34
x = 34/34
x = 1 cm
Therefore, the adjacent sides are 5 cm and 12 cm respectively.
i.e. l = 12 cm, b = 5 cm
Length of the diagonal = √(l² + b²)
= √(12² + 5²)
= √(144 + 25)
= √169
= 13 cm
Hence, the length of the diagonal is 13 cm.

Q4: The angles of a quadrilateral are in the ratio of 1 : 2 : 3 : 4. What is the measure of the four angles?
Sol: Given,
The ratio of the angles of quadrilaterals = 1 : 2 : 3 : 4
Let the four angles of the quadrilateral be x, 2x, 3x, and 4x respectively.
The sum of four angles of a quadrilateral is 360°.
Therefore,
x + 2x + 3x + 4x = 360°
10x = 360°
x = 360°/10
x = 36°
Therefore,
First angle = x = 36°
Second angle = 2x = 2 × 36 = 72°
Third angle = 3x = 3 × 36 = 108°
Fourth angle = 4x = 4 × 36 = 144°
Hence, the measure of four angles is 36°, 72°, 108° and 144°.

Q5: In a quadrilateral ABCD, the measure of the three angles A, B and C of the quadrilateral is 110°, 70° and 80°, respectively. Find the measure of the fourth angle.
Sol: Let,
∠A = 110°
∠B = 70°
∠C = 80°
∠D = x
We know that the sum of all internal angles of quadrilateral ABCD is 360°.
∠A + ∠B+ ∠C+∠D = 360°
110° + 70° + 80° + x = 360°
260° + x = 360°
x = 360° – 260°
x = 100°
Therefore, the fourth angle is 100°.

Q6: A quadrilateral has three acute angles, each measure 80°. What is the measure of the fourth angle?
Sol: Let x be the measure of the fourth angle of a quadrilateral.
Sum of the four angles of a quadrilateral = 360°
80° + 80° + 80° + x = 360°
x = 360° – (80° + 80° + 80°)
x = 360° – 240°
x = 120°
Hence, the fourth angle is 120°.

Q7: In a quadrilateral ABCD, ∠D is equal to 150° and ∠A = ∠B = ∠C. Find ∠A, ∠B and ∠C.
Sol: Given,
∠D = 150°
Let ∠A = ∠B = ∠C = x
By angle sum property of quadrilateral,
∠A + ∠B + ∠C + ∠D = 360°
x + x + x +∠D = 360°
3x +∠D = 360°
3x = 360° – ∠D
30 = 360° – 150°
3x = 210°
x = 70°
Hence, ∠A = ∠B = ∠C = 70°.

Q8: In quadrilaterals,
(i) which of them have their diagonals bisecting each other?
(ii) which of them have their diagonal perpendicular to each other?
(iii) which of them have equal diagonals?
Sol:
(i) Diagonals bisect each other in:

• Parallelogram
• Rhombus
• Rectangle
• Square
• Kite

(ii) Diagonals are perpendicular in:

• Rhombus
• Square
• Kite

(iii) Diagonals are equal to each other in:

• Rectangle
• Square

Q9: The opposite angles of a parallelogram are (3x + 5)° and (61 – x)°. Find the measure of four angles.
Sol:
Given,
(3x + 5)° and (61 – x)° are the opposite angles of a parallelogram.
We know that the opposite angles of a parallelogram are equal.
Therefore,
(3x + 5)° = (61 – x)°
3x + x = 61° – 5°
4x = 56°
x = 56°/4
x = 14°
⇒ 3x + 5 = 3(14) + 5 = 42 + 5 = 47
61 – x = 61 – 14 = 47
The measure of angles adjacent to the given angles = 180° – 47° = 133°
Hence, the measure of four angles of the parallelogram are 47°, 133°, 47°, and 133°.

Q10: Find the measure of all four angles of a parallelogram whose consecutive angles are in the ratio 1 : 3.
Sol:
Given,
The ratio of two consecutive angles of a parallelogram = 1 : 3
Let x and 3x be the two consecutive angles.
We know that the sum of interior angles on the same side of the transversal is 180°.
Therefore, x + 3x = 180°
4x = 180°
x = 180°/4
x = 45°
⇒ 3x = 3(45°) = 135°
Thus, the measure of two consecutive angles is 45° and 135°.
As we know, the opposite angles of a parallelogram are equal.
Hence, the measure of all the four angles is 45°, 135°, 45°, and 135°.

Q11:  How many sides do a regular polygon have, if the measure of an exterior angle is given as 24° ?
Sol: In a regular polygon, all exterior angles are congruent (have the same measure), and the sum of exterior angles of any polygon is always 360°.
The formula for the measure of each exterior angle of a regular polygon is:
Measure of each exterior angle = 360° / Number of sides
Given that the measure of an exterior angle is 24°, we can use this formula to find the number of sides:
24° = 360° / Number of sides
To solve for the number of sides (n):
n = 360° / 24°
n = 15
So, a regular polygon with an exterior angle measuring 24° has 15 sides.

Q12:What is the measure of each exterior angle of a regular polygon of 15 sides?
(a) 30°
(b) 45°
(c) 60°
(d) 24°
Ans: (d)
Sol: The sum of the exterior angles of any polygon, regardless of the number of sides, is always 360°.
In a regular polygon, all exterior angles are congruent, so to find the measure of each exterior angle, we divide the sum of exterior angles by the number of sides.
For a regular polygon with 15 sides:
Measure of each exterior angle = 360° / 15 = 24°
So, the correct answer is (d) 24°.

Q13: When the sum of the internal angles of a polygon is 10 right angles, then how many sides does it have?
(a) 6
(b) 5
(c) 8
(d) 7
Ans: (d)
Sol: The sum of the internal angles of a polygon can be found using the formula: Sum = (n - 2) * 180°, where n is the number of sides of the polygon.
Given that the sum of the internal angles is 10 right angles, which is equivalent to 10 * 90° = 900°, we can set up the equation:
(n - 2) x 180° = 900°
Dividing both sides by 180°:
n - 2 = 5
Adding 2 to both sides:
n = 7
So, the polygon has 7 sides.
The correct answer is (d) 7.

Q14: When one angle of a parallelogram is a right angle, then what is the name of the quadrilateral?
(a) kite
(b) rectangle
(c) rhombus
(d) square
Ans: (b)
Sol: A rectangle is a type of parallelogram where all angles are right angles.

Q15: Select a false statement from those given below:
(a) A square is a rectangle that has equal adjacent sides
(b) A square is a rhombus whose one angle is a right angle
(c) The diagonals of a square bisect each other at right angles
(d) The diagonals of a square do not divide the whole square into four equal parts.
Ans: (d)
Sol: In a square, the diagonals do divide the square into four equal parts.