Previous Year Question: Binary Search Tree: | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Q1: You are given a set V of distinct integers. A binary search tree T is created by inserting all elements of V one by one, starting with an empty tree. The tree T follows the convention that, at each node, all values stored in the left subtree of the node are smaller than the value stored at the node. You are not aware of the sequence in which these values were inserted into T, and you do not have access to T. Which one of the following statements is TRUE? (2024 SET 2)
(a) In order traversal of T can be determined from V
(b) Root node of T can be determined from V
(c) Preorder traversal of T can be determined from V
(d) Post order traversal of T can be determined from V
Ans: (a)
Sol: In order traversal of a binary search tree gives the sorted tree as it will traverse left root right. Also as we have the set V so we can arrange this in increasing order and derive the in order traversal of the BST.
Q2: Suppose a binary search tree with 1000 distinct elements is also a complete binary tree. The tree is stored using the array representation of binary heap trees. Assuming that the array indices start with 0, the 3rd largest element of the tree is stored at index _______. (2022)
(a) 510
(b) 999
(c) 509
(d) 501
Ans: (c)
Sol: For 1000 elements, there will be 10 levels (root is at level 1). But last level will not be completely filled since there are only 1000 elements.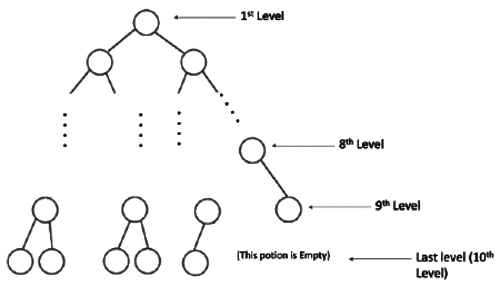
As you can see, some portion is empty. Since largest element can not have children as there are not enough nodes. – we need 1023 nodes to fill all levels.
Now lets see if A in below diagram has children ?
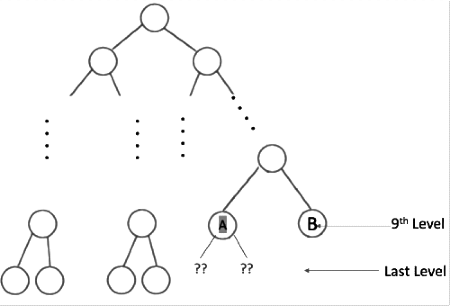
Again, we do not have enough nodes that’s why A will not be having subtree. (This is key point in this question, let’s have a quick explanation of why A doesn't have any children.)
Total nodes till 2nd last level = 29−1 = 511
If we want to fill the last level completely, we need = 210− 1 = 1023 nodes.
A and B can have just 2 children each, so for 1023-4 = 1019 nodes, A and B does not have children.
for 1020 nodes, A has a left child
for 1021 nodes, A has both children, for 1022 nodes, B has a left child, and for 1023 nodes, B has both children.
Now,
largest will be at rightmost of 9th level, (Easy to see…..just keep going right) 2nd largest will at rightmost of 8th level, (because if you want to find larger than this then you need to go on right side and there is just one element on right side)
Where will be 3rd largest ?
Since we know that in order of BST is sorted hence 3rd largest will be a element just before 2nd largest in in order. What we call such element ? – in order predecessor.
Hence 3rd largest will be in order predecessor of 2nd largest. – which is A in above diagram.
Lets find index of 2nd largest then we can find index of 3rd largest.
 index of 2nd largest. (Assuming index starts from 1)
index of 2nd largest. (Assuming index starts from 1)
1 → 3 → 7 → 15 → 31 → 63 → 127 → 255
index of 3rd largest = 510
Since indices are starting from 0 hence answer is 509
Q3: A binary search tree T contains n distinct elements. What is the time complexity of picking an element in T that is smaller than the maximum element in T? (2021 SET 1)
(a) Θ(n log n)
(b) Θ(n)
(c) Θ(log n)
(d) Θ(1)
Ans: (d)
Sol: If our data structure contains n distinct elements then:
In all the standard data structures that we know/study about, If we want to pick/find an element that is not maximum (smaller than maximum) then time complexity will be Θ (1) because we only need to compare any two elements. Take any two elements that you can access in constant time, compare them, and return the smaller of those two elements.
PS: By “standard data structures that we know/study about” I mean the following :
Binary tree, Binary search tree, AVL tree, sorted or unsorted array, linked lists, arrays, stacks, queues, hash tables, heaps, etc.
NOTE: We don’t need to find the “Second Largest Number”. We need ANY number which is not the largest. So, take ANY two elements & the smaller in them is your answer. So, O(1) time is required.
Q4: The preorder traversal of a binary search tree is 15,10,12,11,20,18,16,19. Which one of the following is the post order traversal of the tree? (2020)
(a) 10,11,12,15,16,18,19,20
(b) 11,12,10,16,19,18,20,15
(c) 20,19,18,16,15,12,11,10
(d) 19,16,18,20,11,12,10,15
Ans: (b)
Sol: Preorder traversal of BST:15,10 ,12,11,20,18,16,19
In Pre-order, the first node is ROOT. So root is 15.
In Post-order, the last node is ROOT. So in the Post-order sequence,15 must be at last.
In Pre-order, the second node is the left child of ROOT, if it is less than the root.
Sequence : 10,12,11 belongs to the left sub-tree of ROOT.
10,12,11 is a Preorder of BST -- repetitively apply the steps.
In the Pre-order, the nodes which are greater than ROOT are on the right side of ROOT.
Sequence : 20,18,16 ,19 belongs to the right sub-tree of ROOT.
20,18,16,19 is a Preorder of BST -- repetitively apply the steps.
 Finally we will get 11,12,10 ,16,19,18 ,20 ,15 as Post order.
Finally we will get 11,12,10 ,16,19,18 ,20 ,15 as Post order.
Q5: The pre-order transversal of a binary search tree is given by 12, 8, 6, 2, 7, 9, 10, 16, 15, 19, 17, 20. Then the post-order traversal of this tree is: (2017 SET 2)
(a) 2,6,7,8,9,10,12,15,16,17,19,20
(b) 2,7,6,10,9,8,15,17,20,19,16,12
(c) 7,2,6,8,9,10,20,17,19,15,16,12
(d) 7,6,2,10,9,8,15,16,17,20,19,12
Ans: (b)
Sol: Preorder:  6 2 7 9 10 16 15 19 17 20
6 2 7 9 10 16 15 19 17 20
In order of BST must be sorted in increasing order!


So, Post order: 2 7 6 10 9 8 15 17 20 19 16 12.
Q6: Let T be a binary search tree with 15 nodes. The minimum and maximum possible heights of T are : Note: The height of a tree with a single node is 0. (2017 SET 1)
(a) 4 and 15 respectively
(b) 3 and 14 respectively
(c) 4 and 14 respectively
(d) 3 and 15 respectively
Ans: (b)
Sol: The maximum height of a binary search tree will be when the tree is fully skewed
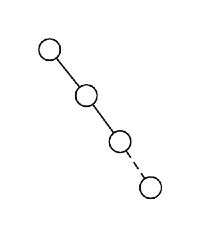
Maximum height = n − 1 = 15 – 1 = 14
The minimum height of a binary search tree will be when the tree is full.
 Minimum height = log2(n+1)-1=log2(15+1) -1=log2(16)-1=4-1 =3
Minimum height = log2(n+1)-1=log2(15+1) -1=log2(16)-1=4-1 =3
Q7: The number of ways in which the numbers 1,2,3,4,5,6,7 can be inserted in an empty binary search tree, such that the resulting tree has height 6, is _____. Note: The height of a tree with a single node is 0. (2016 SET 2)
(a) 2
(b) 8
(c) 64
(d) 32
Ans: (c)
Sol: We need to fill 7levels with 7elements. So, at each level, we have exactly 2 possible options like 1 and 7 for root- one corresponding to going left and the other corresponding to going right. This is the same for all levels up to 6 giving 26= 64 possible ways. In extreme cases, we can get fully left-skewed or right-skewed trees and otherwise, the shape of the tree will be some form of zigzag (every node having a single child).
Q8: While inserting the elements 71, 65, 84, 69, 67, 83 in an empty binary search tree (BST) in the sequence shown, the element in the lowest level is (2015 SET 3)
(a) 65
(b) 67
(c) 69
(d) 83
Ans: (b)
Sol: The Constructed Binary Search Tree from the given Elements will be
 Clearly, the element in the lowest level in the above BST is 67. So,
Clearly, the element in the lowest level in the above BST is 67. So,
Q9: What are the worst-case complexities of insertion and deletion of a key in a binary search tree? (2015 SET 1)
(a) Θ(log n)
(b) Θ ( n ) for both insertion and deletion
(c) Θ ( n ) for insertion and Θ ( l o g n )for deletion
(d) Θ ( l o g n ) for insertion and Θ ( n ) for deletion
Ans: (b)
Sol: Option B, both happens when the BST is skewed.
What is a Skewed Tree?
A binary tree which is dominated solely by left child nodes or right child nodes is called a skewed binary tree or more specifically left skewed binary tree or right skewed binary tree respectively.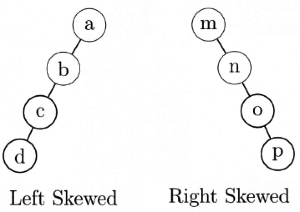
Q10: Which of the following is/are correct in order traversal sequence(s) of binary search tree(s)? (2015SET 1)
I. 3, 5, 7, 8, 15, 19, 25
II. 5, 8, 9, 12, 10, 15, 25
III. 2, 7, 10, 8, 14, 16, 20
IV. 4, 6, 7, 9 18, 20, 25
(a) I and IV only
(b) II and III only
(c) II and IV only
(d) II only
Ans: (a)
Sol: In order traversal of key are always in ascending order.
So, here I & IV th sequence are in ascending order so Option A is Answer.
Q11: The preorder traversal sequence of a binary search tree is 30, 20, 10, 15, 25, 23, 39, 35, 42. Which one of the following is the post order traversal sequence of the same tree? (2013)
(a) 10, 20, 15, 23, 25, 35, 42, 39, 30
(b) 15, 10, 25, 23, 20, 42, 35, 39, 30
(c) 15, 20, 10, 23, 25, 42, 35, 39, 30
(d)15, 10, 23, 25, 20, 35, 42, 39, 30
Ans: (d)
Sol: Since it is a binary search tree, its in order traversal produces a sorted sequence i.e. 10, 15, 20, 23, 25, 30, 35, 39, 42 .
Now given in order and preorder traversals, we get following tree : =From this, we can give post order traversal sequence as 15, 10, 23, 25, 20, 35, 42, 39, 30 i.e.
=From this, we can give post order traversal sequence as 15, 10, 23, 25, 20, 35, 42, 39, 30 i.e.
, option (D).
Q12: Which one of the following is the tightest upper bound that represents the time complexity of inserting an object into a binary search tree of n nodes? (2013)
(a) O(1)
(b) O( log n)
(c) O(n)
(d) O(n log n)
Ans: (c)
Sol: Suppose that we need to insert a node z such that k = k e y [ z ] . Using binary search we find a nil such that replacing it by z does not break the BST-property
BST-Insert ( x , z , k )
1. : if x = n i l then return “Error”
2. : y ← x
3. : while true do {
4. : if k e y [ y ] < k
5. : then z ← l e f t [ y ]
6. : else z ← r i g h t [ y ]
7. : if z = n i l break
8. : } : if k e y [ y ] > k then l e f t [ y ] ← z
9. : else right[p [y]] ←z
Time Complexity Analysis :
1. Best Case = O(1) , When it is smallest/greatest element and BST contains only all greater/smaller element than inserting element respectively.
2. Av g Case = O(log n) , When it belongs between some elements .
3. Worst Case = O (n) , When it is smallest/greatest element and BST contains only all smaller/greater element than inserting element respectively.
Q13: We are given a set of n distinct elements and an unlabeled binary tree with n nodes. In how many ways can we populate the tree with the given set so that it becomes a binary search tree? (2011)
(a) 0
(b) 1
(c) n!
(d) 1/n+1
Ans: (b)
Sol: With n nodes, there are
Corresponding to each structure, only one binary search tree (BST) can be formed because in order is fixed.
Here, we are already given one such structure therefore only one tree possible.
If binary trees would have been asked, n ! trees would have been possible corresponding to each distinct tree structure. Here, tree structure is fixed and hence, we can have only one possibility for BST as elements are distinct. For general cases:
Q14: How many distinct BSTs can be constructed with 3 distinct keys? (2008)
(a) 4
(b) 5
(c) 6
(d) 9
Ans: (b)
Sol: For number of distinct BSTs with n nodes we apply the formula
 n=3 here , so C (6,3)=20
n=3 here , so C (6,3)=20
So, =20/4=5
=20/4=5
Q15: A Binary Search Tree (BST) stores values in the range 37 to 573. Consider the following sequence of keys. (2008)
I. 81,537,102,439,285,376,305
II. 52,97,121,195,242,381,472
III. 142,248,520,386,345,270,307
IV. 550,149,507,395,463,402,270
Which of the following statements is TRUE?
(a) I, II and IV are in order sequences of three different BSTs
(b) I is a preorder sequence of some BST with 439 as the root
(c) II is an in order sequence of some BST where 121 is the root and 52 is a leaf
(d) IV is a post order sequence of some BST with 149 as the root
Ans: (c)
Sol:
A. Incorrect because I & IV are not in ascending order.(In order sequence of BST is in increasing order)
B. I is a preorder sequence of some BST with 439 as the root . False because if 439 is root, it should be first element in preorder.
This is correct.
D. IV is a post order sequence of some BST with 149 as the root, False because if 149 is root, it should be last element in post order
Q16: A Binary Search Tree (BST) stores values in the range 37 to 573. Consider the following sequence of keys. (2008)
I. 81,537,102,439,285,376,305
II. 52,97,121,195,242,381,472
III. 142,248,520,386,345,270,307
IV. 550,149,507,395,463,402,270
Suppose the BST has been unsuccessfully searched for key 273. Which all of the above sequences list nodes in the order in which we could have encountered them in the search?
(a) II and III only
(b) I and III only
(c) III and IV only
(d) III only
Ans: (d)
Sol: The question goes like this. IF there had been 273 in the actual sequence then which of the following search sequences would have been successful.
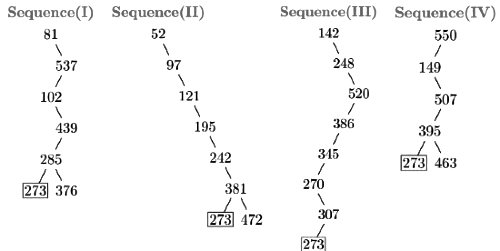
In sequence 1 no need to go from 285 to 376 as 273 is less than 285.
In sequence 2 no need to go from 381 to 472 as 273 is less than 381 .
In sequence 4 no need to go from 395 to 463 as 273 is less than 395.
In sequence 3 number 273 might have been to the left of 307 and search would have been successful.
Q17: Which of the following is TRUE? (2008)
(a) The cost of searching an AVL tree is Θ(log n) but that of a binary search tree is O(n)
(b) The cost of searching an AVL tree is Θ(log n) but that of a complete binary tree is Θ(n log )
(c) The cost of searching a binary search tree is O(log n) but that of an AVL tree is Θ(n)
(d) The cost of searching an AVL tree is Θ (n log n)but that of a binary search tree is O(n)
Ans: (b)
Sol: A) is true as AVL tree is a balanced search tree that has time complexity of searching Θ( log n ) ,
but in binary search tree, we can have a completely left/right skewed tree, in which search is 0(n)
Q18: You are given the post order traversal, P, of a binary search tree on the n elements 1, 2,...,n. You have to determine the unique binary search tree that has P as its post order traversal. What is the time complexity of the most efficient algorithm for doing this? (2008)
(a) Θ (log n)
(b) Θ(n)
(c) Θ (n log n)
(d) None of the above, as the tree cannot be uniquely determined
Ans: (b)
Sol: Last element in post order is the root of tree- find this element in in order- log n time. Now as in quick sort consider this as pivot and split the post order array into 2- possible because all elements smaller than pivot goes to left and all elements larger than pivot goes to right and suppose we have x elements smaller than pivot, these elements will be same in both in order as well as post order (order may change). We already got the root, now left child is the left split and right child is the right split.
So, doing this recursively gives time complexity of this approach as
T(n) =t(k) +T (n-k-1+ log n
Solving would give T(n=O( n log n) in worst case, by putting k = 0 and shown at bottom.
But searching for an element in the in order traversal of given BST can be done in O(1) because we have n elements from 1. . n so there is no need to search for an element- if last element in post order is say 5 we take it as root and since 4 elements (1. .4) are smaller we split the post order array in to two- (first 4 elements), (6 th element onward) and solve recursively. Time complexity for this would be
T(n) =t(k) +T (n-k-1+ O(1)
which gives T(n) = O(n) .
Since we know that all elements must be traversed at least once, T( n ) = Ω (n) also and so
T (n) = Θ (n).
The following code is doing this.


 T(n) = T(k) + T(n − k − 1 ) + log n
T(n) = T(k) + T(n − k − 1 ) + log n
Solving would give T ( n ) = O ( n log n ) , by putting k = 0 ,
T (n) = T(0) +T (n − 1) + log n ,
⟹T(n) =O(1) +log n +log (n − 1)+log (n −2) + ⋯ + log 1
⟹T (n) = n +log n !
⟹T (n) = O(n log n).
PS: Even for a general BST, given a post order traversal, we can construct the BST in O(n) more stricter than O (n log n) derived above and this matches Ω (n) and hence we do have an Θ (n) algorithm. This algorithm can be seen at below link
Q19: When searching for the key value 60 in a binary search tree, nodes containing the key values 10, 20, 40, 50, 70, 80, 90 are traversed, not necessarily in the order given. How many different orders are possible in which these key values can occur on the search path from the root to the node containing the value 60? (2007)
(a) 35
(b) 64
(c) 128
(d) 5040
Ans: (a)
Sol: 10 , 20 , 40 , 50 , 70 , 80 , 90
In BST search we if we go from say 10 to 40 while searching for 60 , we will never encounter 20 . So, 10 , 20 , 40 and 50 visited, means they are visited in order. Similarly, 90 , 80 and 70 are visited in order. So, our required answer will be
(Since only one permutation is valid for both the smaller set of numbers as well as larger set of numbers)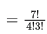
= 35
Q20: Suppose that we have numbers between 1 and 100 in a binary search tree and want to search for the number 55. Which of the following sequences CANNOT be the sequence of nodes examined? (2006)
(a) {10,75,64,43,60,57,55}
(b) {90,12,68,34,62,45,55}
(c) {9,85,47,68,43,57,55}
(d) {79,14,72,56,16,53,55}
Ans: (c)
Sol:
Case 1: Consider the following example, If x < q, then we will only search the left subtree of q, and no element can be greater than q there, so if anything greater than x comes later in the left subtree that must be less than q. Now consider this relation recursively, so whenever we encounter an element that is greater than x, that must be less than the previous element greater than x we encountered. So all the elements greater than x we encounter during probing, that must be in a decreasing sorted order in a valid probe sequence.

Case 2: Consider the following example, If x > q, then we will only search the right subtree of q, and no element can be less than q there, so if anything less than x comes later in the right subtree that must be greater than q. Now consider this relation recursively, so whenever we encounter an element that is less than x, that must be greater than the previous element less than x we encountered. So all the elements less than x we encounter during probing, that must be in a increasing sorted order in a valid probe sequence.

So our conclusion is that elements greater than x must be in a decreasing order and element less than x must be in an increasing order in a valid probe sequence searching for x.
In option C we can see the elements less than 55 forms the following sequence, 9, 47, 43. Here 47 comes before 43, that violates the condition in case 2 as they must be in increasing order.
Q21: A binary search tree contains the numbers 1,2,3,4,5,6,7,8. When the tree is traversed in pre-order and the values in each node printed out, the sequence of values obtained is 5,3,1,2,4,6,8,7. If the tree is traversed in post-order, the sequence obtained would be (2005 )
(a) 8,7,6,5,4,3,2,1
(b) 1,2,3,4,8,7,6,5
(c) 2,1,4,3,6,7,8,5
(d) 2,1,4,3,7,8,6,5
Ans: (d)
Sol: In order of binary search tree is sorted input sequence
so in order= 1, 2, 3, 4, 5, 6, 7, 8.
preorder= 5, 3, 1, 2, 4, 6, 8, 7.
take 1st value from preorder and find its position in in order sequence .
by doing this u get binary search tree.
after that find post order of tree.
i.e. left child --> right child --> root node
Using these two traversals we can find the preorder traversal of the tree i.e., 2, 1, 4, 3, 7, 8, 6, 5
Q22: The numbers 1 , 2 , . … n 1,2,.…n are inserted in a binary search tree in some order. In the resulting tree, the right subtree of the root contains p nodes. The first number to be inserted in the tree must be (2005)
(a) p
(b) p + 1
(c) n - p
(d) n - p + 1
Ans: (c)
Sol: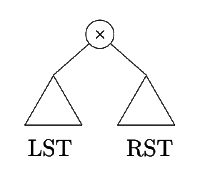 P: # elements in RST
P: # elements in RST
⇒ Depending on X , some number will go LST ∉ RST
⇒
 Remaining elements for LST: n-(p+1)
Remaining elements for LST: n-(p+1)
Q23: How many distinct binary search trees can be created out of 4 distinct keys? (2005)
(a) 5
(b) 14
(c) 24
(d) 42
Ans: (b)
Sol: Number of binary trees with unlabeled n − v e r t i c e s
T ( n ) = T ( 0 ) × T ( n − 1 ) + T (1) × T (n − 2) + . . . + T (n − 1) × T (0)
T 0 (1) = 1
T (4) = T ( 0 ) × T (3) + T (1) × T ( 2 ) + T (2) × T (1) + T (3) × T (0) → eqn #1
T (2) = T ( 0) × T (1) + T (1) × T (0) = 2
T (3) = T (0) × T (2) + T (1) × T (1) + T (2) × T (0) = 2 + 1 + 2 = 5
Q24: Post order traversal of a given binary search tree, T produces the following sequence of keys (2005)
10, 9, 23, 22, 27, 25, 15, 50, 95, 60, 40, 29
Which one of the following sequences of keys can be the result of an in-order traversal of the tree T?
(a) 9, 10, 15, 22, 23, 25, 27, 29, 40, 50, 60, 95
(b) 9, 10, 15, 22, 40, 50, 60, 95, 23, 25, 27, 29
(c) 29, 15, 9, 10, 25, 22, 23, 27, 40, 60, 50, 95
(d) 95, 50, 60, 40, 27, 23, 22, 25, 10, 9, 15, 29
Ans: (a)
Sol: In order traversal of b binary search tree returns the element in sorted order - ascending (in order is left parent then right. in a bs left is less than parent and right is greater than parent). In this option A is the only sorted list. hence it is the only possibility.
Q25: The following numbers are inserted into an empty binary search tree in the given order: 10, 1, 3, 5, 15, 12, 16. What is the height of the binary search tree (the height is the maximum distance of a leaf node from the root)? (2004)
(a) 2
(b) 3
(c) 4
(d) 6
Ans: (b)
Sol: Height is 3
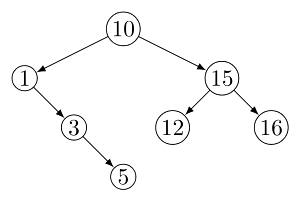
Q26: Suppose the numbers 7, 5, 1, 8, 3, 6, 0, 9, 4, 2 are inserted in that order into an initially empty binary search tree. The binary search tree uses the usual ordering on natural numbers. What is the in order transversal sequence of the resultant tree ? (2003)
(a) 7 5 1 0 3 2 4 6 8 9
(b) 0 2 4 3 1 6 5 9 8 7
(c) 0 1 2 3 4 5 6 7 8 9
(d) 9 8 6 4 2 3 0 1 5 7
Ans: (c)
Sol: In-order traversal returns the elements in ascending (smallest to largest) order.
Q27: Let T(n) be the number of different binary search trees on n distinct elements. (2003)
Then T ( n ) =  T ( k − 1 ) T ( x ) ,
T ( k − 1 ) T ( x ) ,
where x is
(a) n-k+1
(b) n-k
(c) n-k-1
(d) n-k-2
Ans: (b)
Sol: The summation is for each node, if that node happens to be the root. When a node is root, it will have (k−1) nodes on the left sub tree (k being any number) and correspondingly (n−k) elements on the right sub tree. So, we can write recurrence T(k−1) ∗ T(n−k) for the number of distinct binary search trees, as the numbers on left and right sub trees form BSTs independent of each other and only a difference in one of the sub trees produces a difference in the tree.
Knowing the direct formula can also help in getting the answer but is not recommended.
Q28: A binary search tree contains the value 1,2,3,4,5,6,7,8. The tree is traversed in pre-order and the values are printed out. Which of the following sequences is a valid output? (1997)
(a) 5 3 1 2 4 7 8 6
(b) 5 3 1 2 6 4 8 7
(c) 5 3 2 4 1 6 7 8
(d) 5 3 1 2 4 7 6 8
Ans: (d)
Sol : Note: Pre Order means Root-Left-Right Traversal of tree.
By Option Elimination:-
B. False. Because 5 is root so in preorder sequence first 5 elements must contain 1 to 5 But 6 comes here. So false
So, now common things in option A,C,D is 5 , 3 means 5 root then LHS subtree root is 3 . now 3 s LHS is 1 , 2 so they should come first rather than 4 . So option C is False.
Now Check for Option A,D.
Root 5 's RHS is 6 , 7 , 8 now as per Option A,D 7 is Root so 6 should be Left and 8 should be Right so pre order for Right sub tree is 7 , 6 , 8 (Root-L-R). This satisfies option D.
Q29: A binary search tree is generated by inserting in order the following integers: (1996)
50,15,62,5,20,58,91,3,8,37,60,24
The number of nodes in the left subtree and right subtree of the root respectively is
(a) (4,7)
(b) (7,4)
(c) (8,3)
(d) (3,8)
Ans: (b)
Sol: Correct Option: B Root will be 50 . now insert one by one, greater to 50 in the right sub tree, lesser in left sub tree.
Or you can simply count the number looking at the i/p. less than 50 are 7. more than 50 are 4.
|
119 docs|30 tests
|
FAQs on Previous Year Question: Binary Search Tree: - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is a Binary Search Tree (BST)? |  |
| 2. How is a node inserted into a Binary Search Tree (BST)? |  |
| 3. What is the time complexity of searching for a node in a Binary Search Tree (BST)? |  |
| 4. How do you delete a node from a Binary Search Tree (BST)? |  |
| 5. What is the advantage of using a Binary Search Tree (BST) over other data structures? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
















