Previous Year Question: Link List | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Q1: Let SLL del be a function that deletes a node in a singly-linked list given a pointer to the node and a pointer to the head of the list. Similarly, let DLL del be another function that deletes a node in a doubly-linked list given a pointer to the node and a pointer to the head of the list. Let n denote the number of nodes in each of the linked lists. Which one of the following choices is TRUE about the worst-case time complexity of SLL del and DLL del? (2023)
(a) SLL del is O(1) and DLL del is O(n)
(b) Both SLL del and DLL del are O(log(n)
(c) Both SLL del and DLL del are O(1)
(d) SLL del is O(n) and DLL del is O(1)
Ans: (d)
Sol:
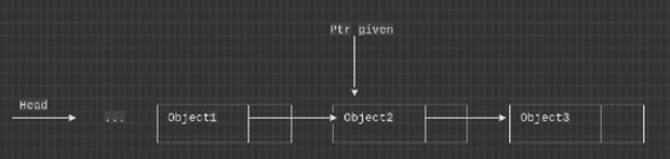
What we can do is traverse from the head pointer to find object 1. Then change the node its pointing to object 3. Then we can free the Object 2.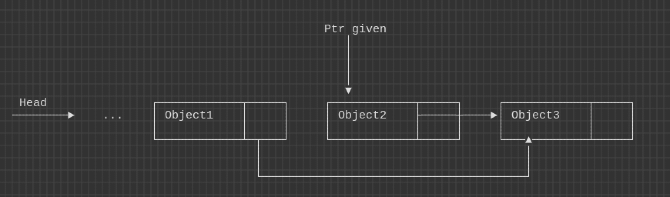
The reason this algorithm is O(n) that we have to traverse from from the head node. To the node just before we want to delete (object 1) here.
Can’t it be done in O(1) by copying?
No, there has been a solution in which some say we swap object3 ↔ object2 and delete object2 node. But what we don’t consider here is the swapping complexity.
If the object that the node holds isn’t swappable O(1) then the complexity would depend upon the complexity to swap.
How O(1) in DLL?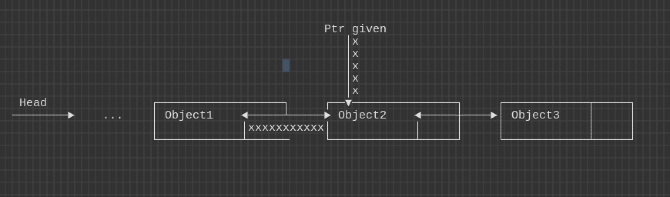 1.I arrive at Object2.
1.I arrive at Object2.
2. Save the pointer to the next node.
3. Traverse the link back to object 1 set the node next to object3.
4. Free object2 node
Each step can be performed in O(1) hence its O(1)
Q2: Consider the problem of reversing a singly linked list. To take an example, given the linked list below, (2022) 
the reversed linked list should look like
Which one of the following statements is TRUE about the time complexity of algorithms that solve the above problem in O(1) space
(a) The best algorithm for the problem takes θ(n) time in the worst case
(b) The best algorithm for the problem takes θ(n log n) time in the worst case.
(c) The best algorithm for the problem takes θ(n2) time in the worst case.
(d) It is not possible to reverse a singly linked list in O(1) space.
Ans: (a)
Sol: Suppose you are given a linked list like this –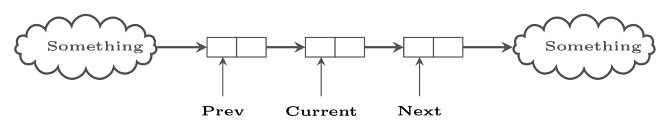 And you want to convert this to as follows-
And you want to convert this to as follows-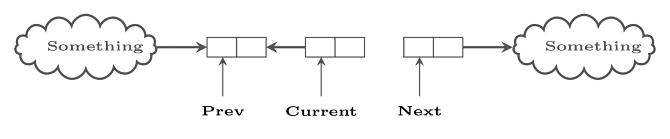
Which means, you just want to change pointer of node that is pointed by current.|
Which line would do same ?
That is all.
Now we just need to shift our pointers – prev, current and next.
Which is also easy Now lets combine all lines together –
Now lets combine all lines together –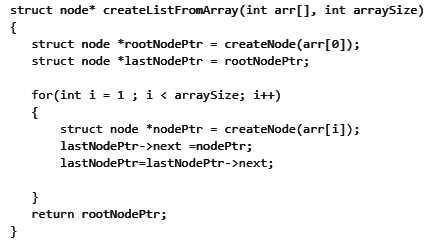 Time complexity –θ(n)
Time complexity –θ(n)
Space Complexity –0(1)
Full working code-
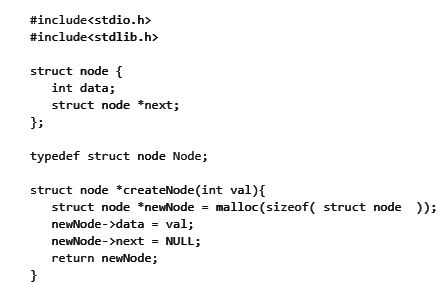


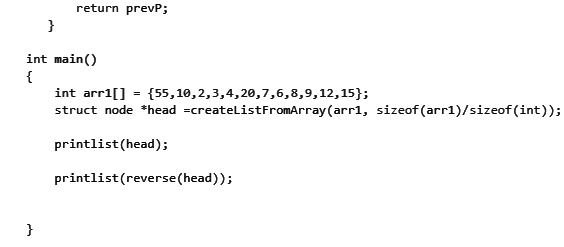
Q3: Consider the following ANSI C program: (2021 SET 2)
Which one of the following statements below is correct about the program?
(a) Upon execution, the program creates a linked-list of five nodes
(b) Upon execution, the program goes into an infinite loop
(c) It has a missing returnreturn which will be reported as an error by the compiler
(d) It dereferences an uninitialized pointer that may result in a run-time error
Ans: (d)
Sol: Lets see the first for loop: After this we get a linked list of size 4 with head pointing to its beginning, and box E and box N ointing to the last node and the next pointer of the last node being uninitialized.
After this we get a linked list of size 4 with head pointing to its beginning, and box E and box N ointing to the last node and the next pointer of the last node being uninitialized.
Now the second for loop will do printing as follows until the second printf of the final iteration
- Value at index 0 is 0
- Value at index 1 is 1
- Value at index 1 is 1
- Value at index 2 is 2
- Value at index 2 is 2
- Value at index 3 is 3
Value at index 3 is 3
After this, the head pointer being uninitialized will be having random content which gets treated as an address. So, when head -> value happens it is basically reading data from uninitialized memory location and so can result (not saying will result because by chance the uninitialized memory can be a valid location) in runtime error.
To correct the error, we just have to add an extra line of code as given below:
Q4: What is the worst case time complexity of inserting n elements into an empty linked list, if the linked list needs to be maintained in sorted order? (2020)
(a) Θ(n)
(b) Θ(n log n)
(c) Θn2)
(d) Θ(1)
Ans: (c)
Sol: "Inserting n elements into an empty linked list, list needs to be maintained in sorted order".
It is not mentioned if the "n elements" are given initially itself or we must insert one element at a time.
1.For the former case, we can just sort the initial n element array - can be done in O(n l g n) and then we'll insert them one by one to the linked list where the sorted order is always maintained. This process will take O(n) and so the entire process can be done in Θ(n l g n) time.
2. For the latter case, where we have to do insertion to the linked list one element at a time, the only way to ensure sorted order for the linked list is to follow insertion sort mechanism. This will take Θn2) time in the worst case.
Since, the question is ambiguous in saying how the elements are presented, both options B and C should be given marks. Unfortunately official key considered later case only. Option C.
Q5: A doubly linked list is declared as: (2018)
 Where Fwd and Bwd represent forward and backward link to the adjacent elements of the list. Which of the following segment of code deletes the node pointed to by X from the doubly linked list, if it is assumed that X points to neither the first nor the last node of the list?
Where Fwd and Bwd represent forward and backward link to the adjacent elements of the list. Which of the following segment of code deletes the node pointed to by X from the doubly linked list, if it is assumed that X points to neither the first nor the last node of the list?
(a) X→ B w d → F w d =X→ F w d; X→F w d →B w d = X →B w d;
(b) X→ B w d. F w d =X→ F w d ;x. F w d → B w d =X→ B w d;
(c) X . B w d → F w d = X . B w d; x → F w d . B w d = X . B w d
(d) X → B w d → F w d = X → B w d; X → F w z → B w d = X → F w d;
Ans: (a)
Sol: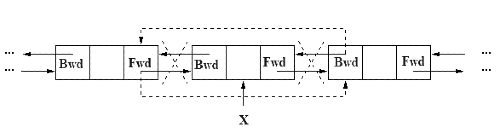
X → B wd → Fwd = X → Fwd
X → F wd → Bwd = X → Bwd
Q6: Consider a singly linked list of the form where F is a pointer to the first element in the linked list and L is the pointer to the last element in the list. The time of which of the following operations depends on the length of the list? (2018)
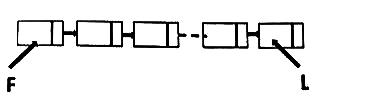 (a) Delete the last element of the list
(a) Delete the last element of the list
(b) Delete the first element of the list
(c) Add an element after the last element of the list
(d) Interchange the first two elements of the list
Ans: (a)
Sol:
A. as we need to traverse (n-1) element to delete n thelement. time taken to do so depends on length of linked list => O(n)
B. Temp=F.
F=F->NEXT
FREE(TEMP)
O(1) and it doesnt depend on the length of list
C. F->NEXT=TEMP;
F=TEMP; WHERE TEMP is our new element
D. CONSTANT TIME OPERATION
Q7: In a doubly linked list the number of pointers affected for an insertion operation will be (2017)
(a) 4
(b) 0
(c) 1
(d) Depends on the nodes of doubly linked list
Ans: (d)
Sol: case 1: If insertion in beginning (assume starting node's pointer name is start)

Q8:Given two statements (2017)
Insertion of an element should be done at the last node of the circular list
Deletion of an element should be done at the last node of the circular list
(a) Both are true
(b) Both are false
(c) First is false and second is true
(d) None of the above
Ans: (b)
Q9: Consider the C code fragment given below. (2017 SET 1)

(a) append list m to the end of list n for all inputs.
(b) either cause a null pointer dereference or append list m to the end of list n.
(c) cause a null pointer dereference for all inputs.
(d) append list n to the end of list m for all inputs.
Ans: (b)
Sol: Here is the implemented code in 



With both n and m and n being non-empty linked list, then,
O/P:
With n being empty linked list, then,
O/P:
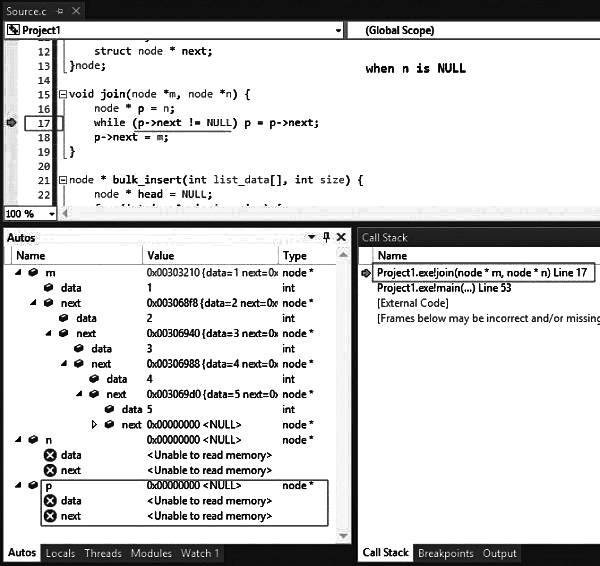
Q 10: N items are stored in a sorted doubly linked list. For a delete operation, a pointer is provided to the record to be deleted. For a decrease-key operation, a pointer is provided to the record on which the operation is to be performed. An algorithm performs the following operations on the list in this order: Θ(N) delete ,O(log N) insert O(log N) find, and Θ(N)decrease−key. What is the time complexity of all these operations put together? (2016 SET 2)
(a) O(log²N)
(b) O(N)
(c) O (N²)
(d) Θ( N² log N)
Ans: (c)
Sol: Delete O(1)
Insert O( N)
Find O( N)
Decrease Key 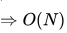 //Because we need to search position in Linked list. (It is similar to a Delete followed by an Insert with the decreased value)
//Because we need to search position in Linked list. (It is similar to a Delete followed by an Insert with the decreased value)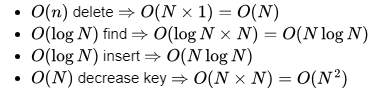
Even though it says at start we got N elements, then we are deleting Q(N) elements, here Q(N) can be anything like N/2,N/4,N /3 and list need not be empty, then above explanation holds !
In case it actually deleted all elements at start analysis will be something like below ⇒
All N elements are deleted, Time complexity O(1) each delete, total delete O(N)
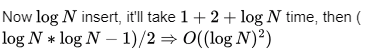
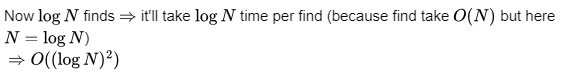
So, size of list * no. of decrease key ⇒Nx log N =O(N log N)
There is no option like O(N log N)
So, correct answer is (ON²)
Q11: An unordered list contains n distinct elements. The number of comparisons to find an element in this list that is neither maximum nor minimum is (2015 SET 2)
(a) Θ(n log n)
(b) Θ(n)
(c) Θ(log n)
(d) Θ(1)
Ans: (d)
Sol: Since all the elements are distinct ,taking any 3 elements from array will greater that one element is smaller and one element is greater than this element.
Example : taking 3,2,1
here 2 is greater than 1 and smaller than 3.
This condition is true for any 3 elements of array. So choosing randomly 3 elements is sufficient to find an element which is neighter maximum nor minimum.
In worst cast out of choosen 3 elements one is maximum ,one is minimum and 3rd is between them. So it is ensured in choosing only 3 elements. thu O(1)
Q12: An algorithm performs (log n)1/2find operations, N insert operations (log n)1/2 delete operations, and (log n)1/2 decrease-key operations on a set of data items with keys drawn from a linearly ordered set. For a delete operation, a pointer is provided to the record that must be deleted. For the decrease-key operation, a pointer is provided to the record that has its key decreased. Which one of the following data structures is the most suited for the algorithm to use, if the goal is to achieve the best total asymptotic complexity considering all the operations? (2015 SET 1)
(a) Unsorted array
(b) Min-heap
(c) Sorted array
(d) Sorted doubly linked list
Ans: (a)
Sol:
So, Unsorted array is the answer.
The operations given can be performed in any order. So, for Min-heap we cannot do the usual Build Heap method. Delete in unsorted array is O(1) as we can just swap the deleted element with the last element in the array and delete the last element.
For sorted-doubly linked-list we cannot do binary search as this would require another array to maintain the pointers to the nodes.
Q13: Consider a single linked list where F and L are pointers to the first and last elements respectively of the linked list. The time for performing which of the given operations depends on the length of the linked list? (a) Delete the first element of the list
(a) Delete the first element of the list
(b) Interchange the first two elements of the list
(c) Delete the last element of the list
(d) Add an element at the end of the list
Ans:(c)
Sol:
A. Delete the first element of the list
Pointer F will be set to the next node, so it does not depend on the length of the linked list.
B. Interchange the first two elements of the list.
Again this can be performed using a temp node and does not depends on the length of the linked list. A. Delete the first element of the list
Pointer F will be set to the next node, so it does not depend on the length of the linked list.
C. Delete the last element of the list
In this we need to get the address of the node just before the last node, because let address of node before the last node is (1000) then we need to set this address to (1000) -› next =NULL
So calculating this address we need to linear search the linked list and so it depends on the length of the linked list.
D. Add an element at the end of the list
Here, we know the address of the last node due to pointer L.So just do L->next=new node. So it does not depends on the length of the linked list.
Q14: The following steps in a linked list (2013)
p = get node ()
info(p) = 10
next (p) = list
list = p
result in which type of operation?
(a) Pop operation in stack
(b) Removal of a node
(c) Inserting a node
(d) Modifying an existing node
Ans(c)
Sol:It is Insertion of node ,
A node have 2 fields associate with it
1. Data ( The information that it conatin )
2 . Next --- ( which point to the next node )
The line P= get node () ; mean you are allocating a space for a new node that you want to create
Then you from second line info(p)=10 mean you are setting the info value to 10
And then you are updating list Field
Q15: The following C function takes a simply-linked list as input argument. It modifies the list by moving the last element to the front of the list and returns the modified list. Some part of the code is left blank. (2010)
 Choose the correct alternative to replace the blank line.
Choose the correct alternative to replace the blank line.
(a) q = NULL; p → next = head; head = p;
(b) q → next = NULL; head = p; p → next = head;
(c) head = p; p → next = q; q → next = NULL;
(d) q → next = NULL; p →next = head; head = p;
Ans: (d)
Sol: As per given code p points to last node which should be head in modified.
q is the previous node of tail which should be tail for modified
Q16: The minimum number of fields with each node of doubly linked list is (2008)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c)
Sol: When question comes like this we should think as a question asking person. I suppose this was meant in an easy way, where we have one data node and two pointers and hence we get 3 fields. With XOR linked list, we can use just one pointer instead of 2 and similarly strictly speaking we do not need a data node also. So, we can get even 1 here. But lets be simple and mark answer as 3.
Q17: Which of the following operations is performed more efficiently by doubly linked list than by linear linked list? (2008)
(a) Deleting a node whose location is given
(b) Searching an unsorted list for a given item
(c) Inserting a node after the node with a given location
(d) Traversing the list to process each node
Ans: (a)
Sol : REASON: In this question, we can simply eliminate the (2) and (4) from our choice, since in both the cases we need to visit every node one after other. Doubly LL will serve no extra good in these two cases as we need to proceed from starting node and go until the last note in LL or vice-versa
(2) To insert a new node in the LL after some specific node, we need not go back to the previous node in the LL. And thus, doubly LL will serve no purpose in this case too.
At last, in the case of (1) we are supposed to delete the node (say x) whose location is given. Which means that before we remove node x from the LL we need to store the address of next node in the list, linked to node x in the address field of node just before node x (which currently store the address of node x). Since we need to go back-and-forth in the list during this operation, doubly linked list will be a good help in increasing the efficiency by decreasing the time required for the operation.
Q18: The time required to search an element in a linked list of length n is (2008)
(a) O(log2n)
(b) O (n)
(c) O(1)
(d) O(n²)
Ans: (b)
Sol: The time required to search an element in a linked list of length n is O(n).
I n the worst case, the element to be searched has to be compared with all elements of linked list.
Q19: The following C function takes a single-linked list of integers as a parameter and rearranges the elements of the list. The function is called with the list containing the integers 1,2,3,4,5,6,7 in the given order. What will be the contents of the list after the function completes execution? (2008)  (a) 1,2,3,4,5,6,7
(a) 1,2,3,4,5,6,7
(b) 2,1,4,3,6,5,7
(c) 1,3,2,5,4,7,6
(d) 2,3,4,5,6,7,1
Ans: (b)
Sol: The loop is interchanging the adjacent elements of the list. But after each interchange, next interchange starts from the unchanged elements only (due to p=q→ next;)
1st iteration: 1,2,3,4,5,6,7
⇒2,1,3,4,5,6,7
2nd iteration: 2,1,4,3,5,6,7
3rd iteration: 2,1,4,36,5,7
p pointing to 7 and q is pointing to NULL(0) as p is false hence q=p ? p →next 0;will return
q=0 ending the loop. (In C language NULL is having the value 0).
Q20: The following C function takes a singly-linked list of integers as a parameter and rearranges the elements of the list. The list is represented as pointer to a structure. The function is called with the list containing the integers 1,2,3,4,5,6,7 in the given order. What will be the contents of the list after the function completes execution? (2005)
 (a) 1,2,3,4,5,6,7
(a) 1,2,3,4,5,6,7
(b) 2,1,4,3,6,5,7
(c) 1,3,2,5,4,7,6
(d) 2,3,4,5,6,7,1
Ans: (b)
Sol: As p and q are swapping each other where q is p → next all the time .
Q21: Suppose there are ⌈log n⌉ sorted lists of ⌊n/log n⌋ elements each. The time complexity of producing a sorted list of all these elements is: (Hint: Use a heap data structure) (2005)
(a) O(n log log n)
(b) θ (n log n)
(c) Ω (n log n)
(d) Ω(n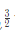 )
)
Ans:(a)
Sol: Since we have log n lists we can make a min-heap of log n elements by taking the first element from each of the log n sorted lists. Now, we start deleting the min-element from the heap and put the next element from the sorted list from which that element was added to the heap. (This identity can be done by making a structure of two values, one for the number and one for identifying the origin sorted list of that number and storing this structure in the heap). In this way each delete and the corresponding insert will take O(log log n) time as delete in heap of size n is O(log n) and inserting an element on a heap of size n is also O(log n) (here, heap size is log n) Now, we have a total of 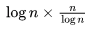 =n elements. So, total time will be O(n log log n)
=n elements. So, total time will be O(n log log n)
Q22: Let P be a singly linked list. Let Q be the pointer to an intermediate node x in the list. What is the worst-case time complexity of the best-known algorithm to delete the node x from the list ? (2004)
(a) O(n)
(b) O(log ² n)
(c) O(log n)
(d) O(1)
Ans: (a)
Sol: PS: We can simulate the deletion by moving the x's next node data to x's next node. But this is technically not the same as DELETING NODE
x as mentioned in the question though effect is the same as long as there are a constant number of elements to be moved from x's next node.
Q23: Suppose each set is represented as a linked list with elements in arbitrary order. Which of the operations among union, intersection, membership, cardinality will be the slowest? (2004)
(a) union only
(b) intersection, membership
(c) membership, cardinality
(d) union, intersection
Ans: (d)
Sol: Membership is linear search - O(n1+n2)
Cardinality is linear - O(n1+n2)
For union we need to ensure no duplicate elements should be present O(n1xn2)
we need to check if that element exists in other set
For intersection also for every element in set1 we need to scan set2 - O(n1xn2)
Q24: A circularly linked list is used to represent a Queue. A single variable p is used to access the Queue. To which node should p point such that both the operations en Queue and deQueue can be performed in constant time? (2004)
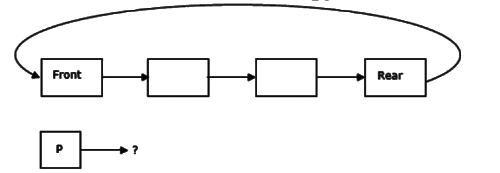
(a) rear node
(b)not possible with a single pointer
(c) front node
(d) node next to front
Ans: (a)
Sol: The pointer points to the Rear node.
E n Queue: Insert new Node after Rear, and make Rear point to the newly inserted node:
 DeQueue: Delete the Front node, and make the second node the front node.
DeQueue: Delete the Front node, and make the second node the front node.
Since there has been a lot of confusion in the comments, let me explain the answer using the pointer `p`
Note that the answer remains unchanged – the below code is just written in a different style.
Q25: Consider the function f defined below. (2003)
 For a given linked list p, the function f returns 1 if and only if
For a given linked list p, the function f returns 1 if and only if
(a) the list is empty or has exactly one element
(b) the elements in the list are sorted in non-decreasing order of data value
(c) the elements in the list are sorted in non-increasing order of data value
(d) not all elements in the list have the same data value
Ans:(b)
Sol:It returns 1 if and only if the linked list is sorted in non-decreasing order- (B) option.
It returns 1 if the list is empty or has just 1 element also, but if and only if makes (A) option false.
Q26: In the worst case, the number of comparisons needed to search a single linked list of length n for a given element is (2002)
(a) log n
(b) n/2
(c) log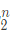 -1
-1
(d) n
Ans: (d)
Sol: A & C are not correct as we can not do binary search efficiently {it takes O(n)} in Linked list.
B seems like average case, be we are asked for worst case
Worst case is we do not find the element in list. We might end up searching entire list & comparing with each element. So, answer -> (D). n
Q27: The concatenation of two lists is to be performed on O(1) time. Which of the following implementations of a list should be used? (1997)
(a )Singly linked list
(b) Doubly linked list
(c) Circular doubly linked list
(d) Array implementation of list
Ans: (c)
Sol: (Circular Doubly linked List)
Analyze below Code which is O(1)
Suppose List1's first element is pointed by pointer p1
And List2's first element is pointed by p2
And tmp is a temporary pointer of node type. Options A&B of linked list are not possible in O(1). Because they cannot find out rear element without doing a linear traversal.
Options A&B of linked list are not possible in O(1). Because they cannot find out rear element without doing a linear traversal.
For Option D. Array implementation requires O(n1+n2)copy operations where n1 and n2 represent the sizes of List1 and List2 respectively.
Q28: Which of the following statements is true? (1995)
I. As the number of entries in a hash table increases, the number of collisions increases.
II. Recursive programs are efficient
III. The worst case complexity for Quicksort is O(n²)
IV. Binary search using a linear linked list is efficient
(a) I and II
(b)II and III
(c)I and IV
(d) I and III
Ans: (d)
Sol:Binary search using a linked list is not efficient as it will not give O(log n),because we will not be able to find the mid in constant time. Finding mid in linked list takes O(n) time.
Recursive programs are not efficient because they take a lot of space, Recursive methods will often throw Stack Overflow Exception while processing big sets. moreover, it has its own advantages too.
Q29: For merging two sorted lists of sizes m+ n, we require comparisons of (1995)
(a) O(m)
(b) O(n)
(c) O(m +n)
(d) O(log m +log n)
Ans: (c)
Sol: The number of moves are however always m + n so that we can term it as Θ m + n . But the number of comparisons varies as per the input. In the best case, the comparisons are min(m, n)and in worst case they are m+n-1.
Q30: Linked lists are not suitable data structures for which one of the following problems? (1994)
(a) Insertion sort
(b) Binary search
(c) Radix sort
(d) Polynomial manipulation
Ans: (b)
Sol: Linked lists are suitable for:
Insertion sort: No need to swap here just find appropriate place and join the link
Polynomial manipulation: Linked List is a natural solution for polynomial manipulation
Radix sort: Here we are putting digits according to same position(unit,tens) into buckets; which can be effectively handled by linked lists.
Not Suitable for:
Binary search: Because finding mid element itself takes O(n) time.
Q31: In a circular linked list organization, insertion of a record involves modification of (1987)
(a) One pointer.
(b) Two pointers.
(c) Multiple pointers.
(d) No pointer
Ans: (b)
Sol: Suppose we have to insert node p after node q then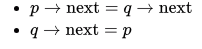
|
159 docs|30 tests
|
FAQs on Previous Year Question: Link List - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is a linked list in computer science? |  |
| 2. What are the advantages of using a linked list? |  |
| 3. What are the different types of linked lists? |  |
| 4. How do you traverse a linked list? |  |
| 5. What are some common operations performed on a linked list? |  |





















