Previous Year Questions: AVL Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Q1: In a balanced binary search tree with n elements, what is the worst case time complexity of reporting all elements in range [a, b]? Assume that the number of reported elements is k. (2020)
(a) Θ(log n)
(b) Θ(log n +k)
(c) Θ(k log n)
(d) Θ(n log k)
Ans: (b)
Sol: First, you'll have to check if the elements a and b are present in the BST or not. Since the BST is balanced, it will take Θ (log 2 (n) ) time for that. Traversing the k elements would take additional Θ (k) time.
Q2: What is the worst case time complexity of inserting n 2elements into an AVL-tree with n elements initially? (2020)
(a) Θ (n4 )
(b) Θ (n2)
(c) Θ (n2 log n)
(d) Θ (n3)
Ans: (c)
Sol: Steps: For worst case (in worst case insertion will cause Ω(log n) operations in an AVL tree where n is the number of nodes present.
1st insertion time complexity = Θ(log n)
2nd insertion time complexity = Θ (log (n +1))
⋮
n2th insertion time complexity = Θ (log (n + n2− 1))
Total number of operations = Θ (log n)+Θ (log (n +1))+ … +Θ(log (n+ n 2 −1))
= Θ (log (n .(n+1).(n+2) … (n+n2−1)))
= Θ (log ) ( ∵ the highest degree term in the log expression will be
) ( ∵ the highest degree term in the log expression will be 
= Θ ( n2(log n)
Q3: Suppose we have a balanced binary search tree T holding n numbers. We are given two numbers L and H and wish to sum up all the numbers in T that lie between L and H. Suppose there are m such numbers in T. If the tightest upper bound on the time to compute the sum is O(n a log b n + mc log d n) the value of a + 10b + 100c + 1000d is _______. (2014 SET 3)
(a) 100
(b) 110
(c) 10
(d) 1010
Ans: (b)
Sol: In worst case for finding L and H it will take O(log n) time as the given tree is balanced binary search tree.
Now there are m elements between L and H . So to traverse m element it will take O(m) time
(traversal algorithm given below). So, total
O(m+ log n ) ⟹ a = 0 , b = 1 , c = 1 , d = 0
∴ 0 + (10 ×1)+(100 ×1) + (1000 × 0) =110.
To find all the numbers from L to H we can do an in order traversal from root and discard all elements before L and after H .
But this has O(n) time complexity. So, we can do a modification to in order traversal and combine with binary search as follows:
1.Find L using binary search and keep all nodes encountered in the search in a stack.
2. After finding L add it to stack as well and initialize sum = 0 .
3. Now, for all nodes in stack, do an in order traversal starting from their right node and adding the node value to sum. If H is found, stop the algorithm.
Q4: The worst case running time to search for an element in a balanced binary search tree with n2 n elements is (2012)
(a) Θ(n log n)
(b) Θn2n
(c) Θ(n)
(d) Θ(log n)
Ans: (c)
Sol: Balanced binary search takesΘ(log n) for n elements in the worst case. So, with (n2n) elements, the worst case time will be
Θ (log (n2n) )
= Θ (log n+ log 2n)
= Θ (log n+ n)
= Θ (n)
Q5: What is the maximum height of any AVL-tree with 7 nodes? Assume that the height of a tree with a single node is 0. (2009)
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (b)
Sol: With 1 node height is 0 .
Max height will come when each level contain min nodes.
Minimum Nodes in an AVL tree with height n is H ( n ) = H ( n − 1 ) + H ( n − 2 ) + 1 .
H(0)= 1 .
H(1) = 2
H(2) = H (1 ) + H (0)+1 = 2 + 1 + 1 = 4
H(3) = H (2)+H (1) + 1 = 4 + 2 + 1 = 7 .
Q6: A program takes as input a balanced binary search tree with n leaf nodes and computes the value of a function g(x) for each node x. If the cost of computing g(x) is min{no. of leaf-nodes in left-subtree of x, no. of leaf-nodes in right-subtree of x} then the worst-case time complexity of the program is (2004)
(a) Θ (n)
(b) Θ (n l o g n)
(c) Θ (n2)
(d) Θ ( n2 log n)
Ans: (b)
Sol: At the root node (first level) the cost would be Θ  as the tree is balanced.
as the tree is balanced.
At next level, we have 2 nodes and for each of them cost of computing g ( x ) will be Θ So, total cost at second level = Θ
So, total cost at second level = Θ . Similarly at each level (total cost per level and not the cost per node in a level) the cost would be Θ
. Similarly at each level (total cost per level and not the cost per node in a level) the cost would be Θ  and so for log n levels it would be Θ(n log n). PS: Even if we change min to max in the definition of g(x) we get the same answer.
and so for log n levels it would be Θ(n log n). PS: Even if we change min to max in the definition of g(x) we get the same answer.
Q7: A weight-balanced tree is a binary tree in which for each node, the number of nodes in the let sub tree is at least half and at most twice the number of nodes in the right sub tree. The maximum possible height (number of nodes on the path from the root to the furthest leaf) of such a tree on n nodes is best described by which of the following ? (2002)
(a) log2n
(b) log4/3n
(c) log3n
(d) log3/2n
Ans: (d)
Sol: Let nI and nr nodes be present in the left and right sub-trees respectively.
We have,  Without loss of generality, let the left sub-tree have greater number of
Without loss of generality, let the left sub-tree have greater number of
nodes (2nrnodes).Then, n r+ 2nr + 1 =n .Thus we get ,nr 
Total number of nodes can be described by the recurrence:
As this makes maximum nodes go to one subtree and that is what we want to get the maximum height with a given number of nodes.
Now, the height of the tree will be H(n) =H (-1)) +1and H(1) =1
(-1)) +1and H(1) =1
We can draw a recurrence tree and the cost at each level is 1, and the height will be log 
Q8: In the balanced binary tree in the below figure, how many nodes will become unbalanced when a node is inserted as a child of the node g? (1996)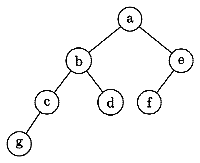 (a) 1
(a) 1
(b) 3
(c) 7
(d) 8
Ans: (b)
Sol:
a , b , c will become unbalanced with Balance factor as + 2 ,+2 ,+2 respectively. Balance factor should be − 1 ,0 ,+1 .
Balance factor = Height(LST) - Height(RST)
Or Balance factor = | Height(LST) - Height(RST) |
|
119 docs|30 tests
|
FAQs on Previous Year Questions: AVL Tree - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is an AVL tree? |  |
| 2. How does an AVL tree maintain balance? |  |
| 3. What is the time complexity of searching in an AVL tree? |  |
| 4. How is an AVL tree different from a regular binary search tree? |  |
| 5. Can an AVL tree become unbalanced? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
















