Previous Year Questions: Asymptotic Notation | Algorithms - Computer Science Engineering (CSE) PDF Download
Q1: Given an integer array of size N, we want to check if the array is sorted (in either ascending or descending order). An algorithm solves this problem by making a single pass through the array and comparing each element of the array only with its adjacent elements. The worst-case time complexity of this algorithm is (2024 SET-1)
(a) both O (N) and Ω (N)
(b) O (N) but not Ω (N)
(c) Ω (N) but not O (N)
(d) Neither O (N) nor Ω (N)
Ans: (a)
Sol: The objective of the algorithm is to check whether the array is sorted or not, and it does so by making a single pass through the array.
For this the worst case will be when the array is already sorted.
Q2: Consider functions Function 1 and Function 2 expressed in pseudocode as follows:
 Let f1 (n) and f2 (n) denote the number of times the statement "x = x + 1" is executed in Function 1 and Function 2, respectively.
Let f1 (n) and f2 (n) denote the number of times the statement "x = x + 1" is executed in Function 1 and Function 2, respectively.
Which of the following statements is/are TRUE? (2023)
(a) f1 (n) ϵ Θ(f2(n))
(b) f1 (n) ϵ ο(f2(n))
(c) f1 (n) ϵ ω(f2(n))
(d) f1 (n) ϵ Ο (n)
Ans: (a, d)
Sol: Function1 iterates for n times.
∴ f1(n) = n
Function2 iterates for 100 ж n times. (Asymptotically n times)
∴ f2(n) = n
So we can conclude,
f1(n) ∈ Θ(f2(n))
f1(n) ∈ o(f2(n))
f1 (n) ∈ Ω(f2(n))
Q3: Let f and g be functions of natural numbers given by f(n) = n and g(n) = n2
Which of the following statements is/are TRUE? (2023)
(a) f ϵ Ο(g)
(b) f ϵ Ω(g)
(c) f ϵ ο(g)
(d) f ϵ Θ(g)
Ans: (a, c)
Sol: Some students might be confused by the “ϵ” symbol in the options, instead of “=”.
Let me tell you that writing f ϵ O(g) is a better (technically correct) way than writing f = Ο(g).
In the option had "=" instead of "ϵ" the answer wouldn’t change.
We write f(n) = O(g(n)) to indicate that a function f(n) is a member of the set O(g(n)) and vice versa.
O(f(n)) is a set. So, writing f ∈ O(g) is a better (technically correct) way than writing f = O(g).
To keep it simple, you can think of f = O(g) as same as f ∈ O(g)
Reference: Introduction to Algorithms by CLRS(Cormen):
A function f(n) belongs to the set Θ (g(n)) if there exist positive constants c1 and c2 such that it can be "sandwiched" between c1g(n) and c2g(n), for sufficiently large n. Because Θ(g(n)) is a set, we could write "f(n) ϵ Θ(g(n))" to indicate that f(n) is a member of Θ(g(n)) . Instead, we will usually write "f(n) = Θ(g(n)) " to express the same notion. You might be confused because we abuse equality in this way, but we shall see later in this section that doing so has its advantages.
Basically, for g(n) = n2, O(g) is a set of functions which grow slowly (or name) as compared to g as input n grows larger.
Hence, O(n2) = {n, n2, logn, 1, constant, nlogn, n1.9,...}
Keep It Simple: f ∈ O(g) is same as f = O(g)
Q4: Which one of the following statements is TRUE for all positive functions f(n)? (2022)
(a) f(n2) = θ(f(n)2), where f(n) is a polynomial
(b) f(n2) = o(f(n)2)
(c) f(n2) = O(f(n)2), where f(n) is an exponential function
(d) f(n2) = Ω(f(n)2)
Ans: (a)
Sol: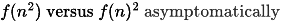
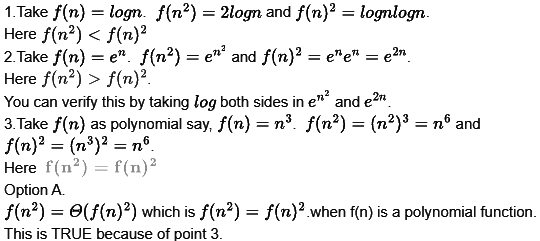
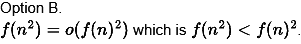
Obviously this is false because it depends on f(n).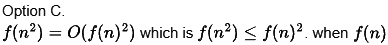 is an exponential function.
is an exponential function.
This is false because of point 2 mentioned above. 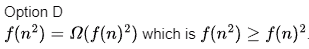
Obviously this is false because it depends on
Q5: Consider the following three functions.
f1 = 10n f2 = nlogn f3 = n√n
Which one of the following options arranges the functions in the increasing order of asymptotic growth rate? (2021 SET-1)
(a) f3, f2, f1
(b) f2, f1, f3
(c) f1, f2, f3
(d) f2, f3, f1
Ans: (d)
Sol: Lets identify the function types
- f1 = 10n- Exponential Function
- f2 = nlog n- Super-polynomial but sub-exponential
- f3 = n√n - Super-polynomial but sub-exponential
So, clearly asymptotic growth of f1
Both
Now, log n
log n = o(√n) ⇒ nlog n = o (n√n). So, asymptotic growth rate of f1, f2,
Q6: What is the complexity of the following code?
Which of the following is not a valid string? (2020)
(a) O(n2)
(b) O(n Log n)
(c) O(n)
(d) O(n log n log n)
Ans: (c)
Sol: Outer loop runs log n
∴ The time complexity will be: O(n log n)
They asked for the invalid string.
So, it will be O(n)
Q7: There are n unsorted arrays: A1, A2, ..., An. Assume that n is odd. Each of A1, A2, ..., An contains n distinct elements. There are no common elements between any two arrays. The worst-case Asymptotic Notation of computing the median of the medians of A1, A2, ..., An is _______ . (2019)
(a) O(n)
(b) O(n log n)
(c) O(n2)
(d) Ω(n2 log n)
Sol: Here is the pseudo code for finding median in linear time.
- For each row find median Mi
using Find Median algorithm. ∀ i Mi ∈ M - Find median of
M
Time complexity: - Total n elements in each row so finding median of a row will take O(n) Time. Total n row so total time n * (O(n)) = O(n2)
- |M|=n so finding median of will take time.
Total time = O(n2) + O(n) = O(n2)
Q8: Consider the following C function 
Asymptotic Notation of fun in terms of θ notation is (2017 SET-2)
(a) θ(n√n)
(b) θ(n2)
(c) θ(nlogn)
(d) θ(n2logn)
Ans: (c)
Sol: Inner for loop is dependent on
It II be something like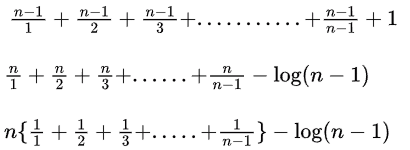
n log(n - 1) - log(n - 1)
n log(n - 1)
n log n
Q9: Match the algorithms with their time complexities: (2017 SET-2)
(a) P-(iii),Q-(iv), R-(i), S-(ii)
(b) P-(iv),Q-(iii), R-(i), S-(ii)
(c) P-(iii),Q-(iv), R-(ii), S-(i)
(d) P-(iv),Q-(iii), R-(ii), S-(i)
Ans: (c)
Sol: According to the recurrence relation of the time complexity of Tower of Hanoi,
T(n) = 2T(n - 1) + 1, we get it is Θ (2n)
Now, heap sort worst case time complexity is Θ (n log n)
Binary Search to search an element given n
Addition of two n x n matrices is Θ(n2)
So, C is correct answer here.
Q10: Consider the following functions from positive integers to real numbers: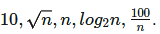
The CORRECT arrangement of the above functions in increasing order of asymptotic complexity is: (2017 SET-1)
(a) 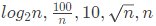
(b) 
(c)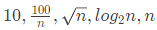
(d)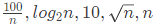
Ans: (b)
Sol: 10 is constant. ∴ Growth rate is 0.
√n grows slower than linear but faster than log. (Consider where as
where as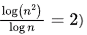
n : Growth rate is linear.
log2 n : Growth rate is logarithmic. For asymptotic growth, the base does not matter.
100/n : Growth rate decreases with n.
So, correct answer is (B).
NOTE: Please never substitute large values of in such questions. If ever you do, at least do for 2 such values and take ratio to get the growth rate or plot a graph.
Remember 1.01n ≠ O (n100).
Q11: In an adjacency list representation of an undirected simple graph G = (V,E), each edge (u,v) has two adjacency list entries: [v] in the adjacency list of u, and [u] in the adjacency list of v. These are called twins of each other. A twin pointer is a pointer from an adjacency list entry to its twin. If |E|=m and |V|=n, and the memory size is not a constraint, what is the Asymptotic Notation of the most efficient algorithm to set the twin pointer in each entry in each adjacency list? (2016 SET-2)
(a) Θ(n2)
(b) Θ(n + m)
(c) Θ(m2)
(d) Θ(n4)
Ans: (b)
Sol: We can take extra array of size V2 as memory is not a constraint.
Do the BFS traversal and for each edge u - v in advance list in graph store the v node address in a|i||j|.
For e.g., if we find 1 → 2 as an edge, then store node 2 node address in location a|i||j|.
Now once we have stored all the edge (u - v) addresses, then do BFS again.
Now when we encounter 1 → 2, then go to a[2][1] which is having twin address and set this twin pointer for node 2 in list 1.
Do for all edges similarly.
Remember, we have not initialized memory as we will use only slots we need. If we initialize memory it can take O(V2) time.
We can also use one hash table per node to store the node address while doing first traversal. The key to has table for Node
is the vertex v (for edge u - v means in u table it has edge to v and we are storing v address) and value will be v address.
Q12: The given diagram shows the flowchart for a recursive function A(n). Assume that all statements, except for the recursive calls, have O(1) Asymptotic Notation. If the worst case Asymptotic Notation of this function is O(na), then the least possible value(accurate up to two decimal positions) of α is. (2016 SET-2)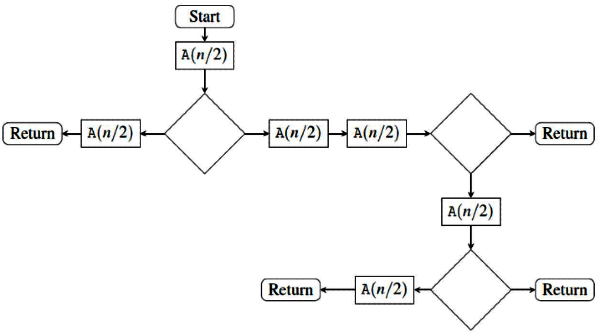
(a) 1.58
(b) 2.32
(c) 2.85
(d) 3.55
Ans: (b)
Sol: If they are asking for worst case complexity hence,
By calling A (n) wet get A (n/2) 5 times,
A(n) = 5A(n/2) + O(1)
Hence, by applying masters theorem ,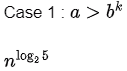
Q13: Consider a carry look ahead adder for adding two n-bit integers, built using gates of fan-in at most two. The time to perform addition using this adder is (2016 SET-1)
(a) Θ(1)
(b) Θ(log(n))
(c) Θ√n
(d) Θ(n)
Ans: (b)
Sol: Look ahead carry generator gives output in constant time if fan in = number of inputs.
Example, it will take O(1) to calculate
c4 = g3 + p3g2 + p3p2g1 + p3p2p1g0 + p3p2p1p0c0,
if OR gate with 5 inputs is present.
If we have 8 inputs, and OR gate with 2 inputs, to build an OR gate with 8 inputs, we will need 4 gates in level- 1, 2 in level-2 and 1 in level-3. Hence, 3 gate delays, for each level.
Similarly an n-input gate constructed with 2-input gates, total delay will be O(log n).
Hence, answer is option B.
Q14: The time complexity of the following C function is (assume n>0) (2015)
(a) O(n)
(b) O(n log n)
(c) O(n2)
(d) O(2n)
Ans: (d)
Sol: 
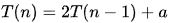 is the recurrence equation found from the pseudo code.
is the recurrence equation found from the pseudo code.
Note: 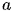 is a constant O(1) cost that the non-recursive part of the function takes.
is a constant O(1) cost that the non-recursive part of the function takes.
Solving the recurrence by Back Substitution:
T(n) = 2T(n - 1) + a
T(n - 1) = 2T(n - 2) + a
T(n - 2) = 2T(n - 3) + a
:
Thus, we can re-write the equation for T(n) as follows
T(n) = 2[2T(n - 2) + a] + a
= 4T(n - 2) + 2a + a
= 4[2T(n - 3) + a] + 3a
= 8T(n - 3) + 4a + 2a + a
:
= 2kT(n - k) + (2k - 1)a
On Substituting Limiting Condition
T(1) = 1 ⇒ n - k = 1 ⇒ k = n - 1
Therefore, our solution becomes
2n-1 + (2n-1 - 1)a = O(2n)
Q15: Let f(n) = n and g(n) = n1+sin n where n is a positive integer. Which of the following statements is/are correct? (2015 SET-3)
I. f(n) = O(g(n))
II. f(n) = Ω(g(n))
(a) Only I
(b) Only II
(c) Both I and II
(d) Neither I nor II
Ans: (d)
Sol: Since the value of sin (n) will always range from -1 to + 1, hence g(n) can take values 1, n , n2.
Hence, if g(n) =1, then statement I is incorrect.
And, if g(n) = n2,then statement II is incorrect.
Q16: Consider the equality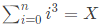 and the following choices for X (2015 SET-3)
and the following choices for X (2015 SET-3)
I. Θ(n4)
II. Θ(n5)
III. O(n5)
IV. Ω(n3)
The equality above remains correct if X is replaced by
(a) Only I
(b) Only II
(c) I or III or IV but not II
(d) II or III or IV but not I
Ans: (c)
Sol: Sum of the cubes of the first n natural numbers is given by (n(n + 1)/2)2 which is Θ(n4).
So, I, III and IV are correct. II is wrong.
∴ (C) is correct.
Q17: Consider the following C function.
Which one of the following most closely approximates the return value of the function fun1? (2015 SET-1)
(a) n3
(b) n(logn)2
(c) nlogn
(d) nlog(logn)
Ans: (d)
Sol: i loop is executing n times, j loop is executing log n times for each i, and so value of p is log n when j loop exits for all iterations of the i loop.
k loop is executing log p times, which is log log n times for each iteration of i. In each of these iteration, q is incremented.
So, over all iterations of i, q will be incremented n log log n times.
Q18: Consider the following function:
The return value of the function is (2013)
(a) Θ(n2)
(b) Θ(n2logn)
(c) Θ(n3)
(d) Θ(n3logn)
Ans: (b)
Sol: The outer loop is running for n/2 times and inner loop is running for log2 n times (each iteration doubles j and j Stops at n
means log2 n times j loop will iterate).
Now in each iteration k is incremented by n/2. So, overall k will be added n/2 * log n * n/2 with an initial value of 0. So, final value of k will be Θ(n2 log n)
Q19: Let W(n) and A(n) denote respectively, the worst case and average case running time of an algorithm executed on an input of size n. Which of the following is ALWAYS TRUE? (2012)
(a) A(n) = Ω(W(n))
(b) A(n) = Θ(W(n))
(c) A(n) = O(W(n))
(d) A(n) = o(W(n))
Ans: (c)
Sol: Worst case complexity can never be lower than the average case complexity, but it can be higher. So,(C) is the answer.
A(n) = O(W(n))
Q20: Which of the given options provides the increasing order of asymptotic complexity of functions f1, f2, f3 and f4? (2011)
f1(n) = 2n;
f2(n) = n3/2;
f3(n) = nlog2n;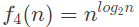
(a) f3, f2, f4, f1
(b) f3, f2, f1, f4
(c) f2, f3, f1, f4
(d) f2, f3, f4, f1
Ans: (a)
Sol: n log2 n < n3/2 is quite straight forward as n3/2 = n x n1/2 and log n < n1/2 as logarithmic growth is smaller than exponential growth however small be the exponentiation factor.
Also, n3/2 < nlog2n and n3/2 < 2n
Now only n log2 n and 2n need to be compared.
Taking log of both (log2 n)2 and n,
n > (log2 n)2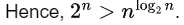
NOTE: We cannot compare two functions for asymptotic growth by taking log if they are giving constants after log operation.
Q21: Two alternative packages A and B are available for processing a database having 10k records. Package A requires 0.0001n2
time units and package B requires 10n log10n time units to process n records. What is the smallest value of k for which package B will be preferred over A? (2010)
(a) 12
(b)10
(c) 6
(d) 5
Ans: (c)
Sol:
10n log10 n ≤ 0.0001n2
⇒ 10 × 10k log10 10k ≤ 0.0001(10k)2
⇒ 10k+1k ≤ 0.0001 × 102k
⇒ k ≤ 102k-k-1-4
⇒ k ≤ 10k-5
Trying the values, 5 doesn't satisfy this but 6 satisfies.
Correct Answer: C
Q22: Arrange the following functions in increasing asymptotic order: (2008)
a. n1/3
b. en
c. p7/4
d. n log9n
e. 1.0000001n
(a) a, d, c, e, b
(b) d, a, c, e, b
(c) d, a, c, e, b
(d) a, c, d, b, e
Ans: (a)
Sol: A< C and A< D are straight forward.
E < B and C, D < E as E and B are exponential functions and B having a larger base.
Now, we just need to see if C or D is larger.
In C we have a term n3/4and correspondingly in D we have log9 n (after taking n out).
n3/4 is asymptotically larger than log9 n as when n =10100, log9n gives 1009, while n3/4gives 1075 > 10037 a much higher value and this is true for all higher values of n. So, D < C.
Thus, A is correct.
Q23: Consider the following C functions:
The running time of f1(n) and f2(n) are (2008)
(a) Θ(n) and Θ(n)
(b) Θ(2n) and Θ(n)
(c) Θ(n) and Θ(2n)
(d) Θ(2n) and Θ(2n)
Ans: (b)
Sol: Time complexity of f1 is given by
T(n) = T(n - 1) + T(n - 2), (multiplication by 2 and 3 won't affect complexity as it is a constant time operation)
T(0) = T(1) = 1
The solution to this (fibonacci series) is given by Golden ratio. which is O(2n). (Using theta in question must be a mistake)
Time complexity of f2 is Θ(n) as here all recursive calls are avoided by saving the results in an array (dynamic programming).
So, answer is (B).
Q24: Consider the following functions:
f(n) = 2n
g(n) = 2!
h(n) = nlogn
Which of the following statements about the asymptotic behaviour of f(n), g(n), and h(n) is true? (2008)
(a) f (n) = O(g(n)); g(n) = O(h(n))
(b) f (n) = Ω(g(n)); g(n) = O(h(n))
(c) g(n) = O(f (n)); h(n) = O(f (n))
(d) h(n) = O(f (n)); g(n) = Ω(f (n))
Ans: (d)
Sol: g(n) = n!
On expanding the factorial we get g(n) = O(nn):
This condition is violated by options A, B and C by first statements of each. Hence, they cannot be said to be TRUE.
Second statement of option D says that g(n) is asymptotically biggest of all.
Answer is option (D).
Q25: The time taken by binary search algorithm to search a key in a sorted array of n elements is (2007)
(a) O(log2 n)
(b) O(n)
(c) O(n log2 n)
(d) O(n2)
Ans: (a)
Q26: Exponentiation is a heavily used operation in public key cryptography. Which of the following options is the tightest upper bound on the number of multiplications required to compute bn mod m, 0 ≤ b, n ≤ m? (2007)
(a) O(log n)
(b) O(√n)
(c) O(n/log n)
(d) O(n)
Ans: (a)
Sol: We need to divide n recursively and compute like following: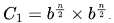 In this, we need to calculate
In this, we need to calculate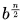 only once.
only once.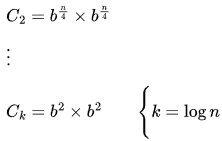
Recurrence relation: T(n) = T(n/2) + O(1)
T(n) = O(log n)
Q27: Consider the following C code segment:
Let T(n)denote the number of times the for loop is executed by the program on input n. Which of the following is TRUE? (2007)
(a) T(n) = O(√n) and T(n) = Ω(√n)
(b) T(n) = O(n) and T(n) = Ω(√n)
(c) T(n) = O(√n) and T(n) = Ω(1)
(d) None of the above
Ans: (c)
Sol: Worst Case : T(n) = O(√n)
Best Case : When n is an even number body of for loop is executed only 1 time (due to "return 0" inside if)
which is irrespective of n ∴ T(n) = Ω(1)
Q28: What is the Asymptotic Notation of the following recursive function: (2007)
(a) Θ(n2)
(b) Θ(nlog2n)
(c) Θ(log2n)
(d) Θ(log 2log2n)
Ans: (d)
Sol: We are asked the time complexity which will be the number of recursive calls in the function as in each call we perform a constant no. of operations and a recursive call. The recurrence relation for this is (considering constant time "c" as 1)
T(n) = T(√N) + 1
= T(n1/4) + 2
= T(n1/8) +3
Going like this we will eventually reach T(3) or T(2). For asymptotic case this doesn't matter and we can assume we reach T(2) and in next step reach T(1). So, all we want to know is how many steps it takes to reach T(1) which will be 1 + no. of steps to reach T(2).
From the recurrence relation we know that T(2) happens when 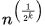 = 2.
= 2.
Taking log and equating,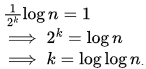
1/2k log n = 1
So, T(1) happens in log log n+1 calls, but for asymptotic complexity we can write as Θ(log log n)
Alternatively,
Substituting values
T(1) = 1
T(2) = 1
T(3) = T(1) + 1 = 2
:
T(8) = T(2) + 1 = 2
T(9) = T(3) + 1 = 3
: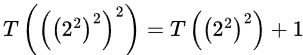
= T(22) + 2
=T(2) + 31 + 3 = 4,
log log n = 3 as n = 256.
log log n = 5 as n = 65536 × 65536 = 232
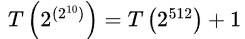
= T(2256) + 2
= T(2128) + 3
= T(264) + 4
= T(232) +5
= T(216) + 6
= T(28) + 7
= T(24) + 8
= T(22) + 9
=T(2) + 10 = 11,
log log n = 10
So, answer is D.
Q29: In the following C function, let n ≥ m.
How many recursive calls are made by this function? (2007)
(a) Θ(logn)
(b) Ω(n)
(c) Θ(loglogn)
(d) Θ(√n)
Ans: (a)
Sol: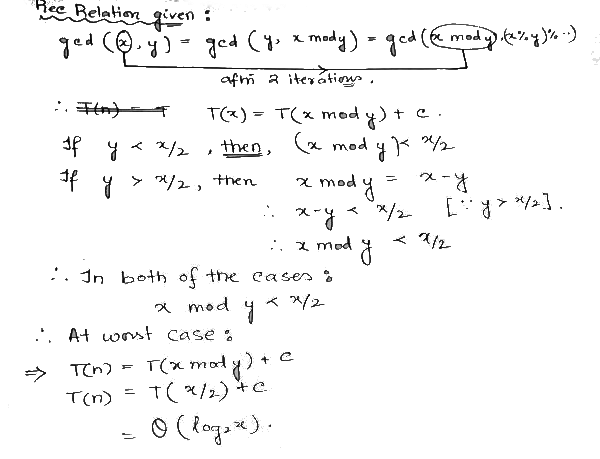
This is how I approached the Problem.
Q30: Consider the following C-program fragment in which i, j, and n are integer variables.
for (i = n, j = θ; i > θ; i/=2, j += i);
Let Val(j) denote the value stored in the variable j after termination of the for loop. Which one of the following is true? (2006)
(a) val(j)=Θ(logn)
(b) val(j)=Θ(sqrt(n))
(c) val(j)=Θ(n)
(d) val(j)=Θ(nlogn)
Ans: (c)
Sol:
j = n/2 + n/4 + n/8 + ... + 1
= n [1/21 + 1/22 + 1/23 + ... + 1/2lg n]
(Sum of first n terms of GP is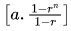 , where a is the first term, r is the common ratio <1, and n is the number of terms)
, where a is the first term, r is the common ratio <1, and n is the number of terms)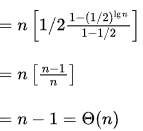
Q31: Consider the following C-function:
Suppose we modify the above function foo() and store the values of foo (i), 0 ≤ i < n, as and when they are computed.
With this modification, the time complexity for function foo() is significantly reduced. The space complexity of the modified function would be: (2005)
(a) O(1)
(b) O(n)
(c) O(n!)
(d) O(nn)
Ans: (b)
Sol:
And here is the present situation :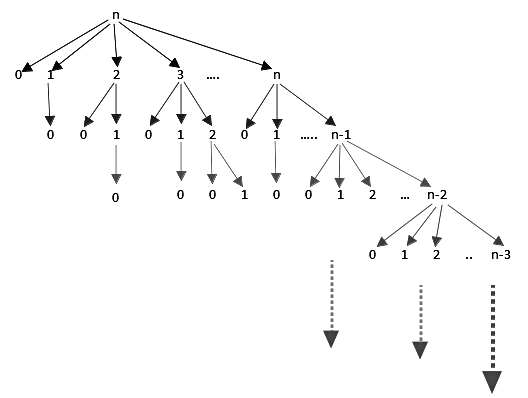
Here we can see that, we have lots of overlapping subproblems. Too many function calls.
- No of function calls = 2n
- stack depth used = O(n)
Therefore space is linear and time is exponential.
If we take a small number say 4, then we would have 8.0 as answer, or we can see that foo(n) = 2n-1
and
- stack depth used = 5.
- No of function calls = 24 = 16.
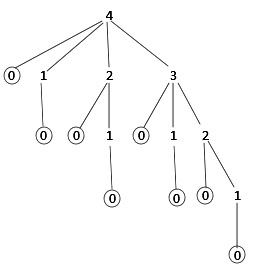
Now, using one-dimensional (1 D) table we can reduce the no of function calls and depth of stack space used as well.
Here is what we want to achieve: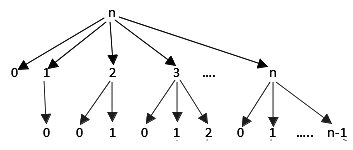
We are reusing already computed foo(x) values. For this purpose, we will be using one 1D array of doubles of size n.
Here is what we are going to do:
- First, check in the 1D table for the required call value.
- If correct value found: do not call recursive functions
- If not, then only attempt for loop recursive calls
Here is the code:
Improvements over given program:
Stack space because of function calls reduced to two level only.
Extra space used for the 1D array = O(n)
More importantly, Time is reduced to O(n2). (Exponential to Quadratic !! )
Overall space complexity = stack + extra = O(1) + O(n) = O(n)
Answer is B.
Q32: Consider the following C-function:
The Asymptotic Notation of space complexity of the above function is: (2005)
(a) O(1)
(b) O(n)
(c) O(n!)
(d) O(nn)
Ans: (b)
Sol: 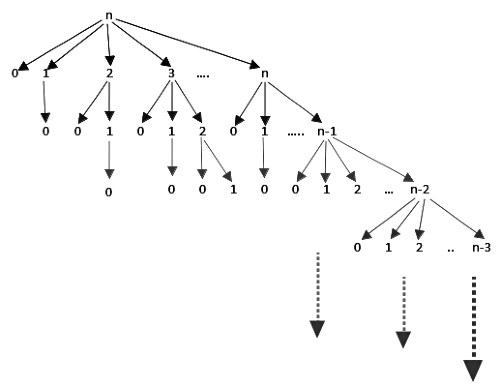
- The code here is storing only local variables. So, the space complexity will be the recursion depth- maximum happening for the last iteration of the for loop - foo(n - 1) - foo(n -2)-....-foo(0) all live giving space complexity O(n).
- To store the n values we need space complexity O(n). So, the space complexity won't change and will be O(n).
Q33: The Asymptotic Notation of computing the transitive closure of a binary relation on a set of n elements is known to be: (2005)
(a) O(n)
(b) O(n log n)
(c) O(n3/2)
(d) O(n3)
Ans: (d)
Sol: Calculating Transitive Closure boils down to Matrix Multiplication.
We can do Matrix Multiplication in O(n3). There are better also that do less than cubic time, but we can not surely do matrix multiplication in
(A) O(n)
(B) O(n log n)
(C) O(n1.5)
Q34: Let f(n), g(n) and h(n) be functions defined for positive integers such that
f(n) = O(g(n)), g(n) ≠ O(f(n)), g(n) = O(h(n)), and h(n) = O(g(n)).
Which one of the following statements is FALSE? (2004)
(a) f(n)+g(n) = O(h(n) +h(n))
(b) f(n) = O(h(n))
(c) h(n) ≠ O(f(n))
(d) f(n)h(n) ≠ O(g(n)h(n))
Ans: (d)
Sol: We can verify as : 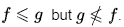 Therefore, f< g.
Therefore, f< g.
Also, g = h, as g = O(h) and h = O(g).
Q35: The Asymptotic Notation of the following C function is (assume n > 0) (2004)
(a) O((n²))
(b) O(nlog n)
(c) O(n)
(d) O((2n))
Ans: (d)
Sol: T(n) = 2T(n - 1) + a is the recurrence equation found from the pseudo code.
Note: a is a constant O(1) cost that the non-recursive part of the function takes.
Solving the recurrence by Back Substitution:
T(n) = 2T(n - 1) + a
T(n - 1) = 2T(n - 2) + a
T(n - 2) = 2T(n - 3) + a
Thus, we can re-write the equation for T(n) as follows
T(n) = 2 [2T(n - 2) + a) + a
= 4T(n - 2) + 2a + a
= 4 [2T(n - 3) + a) + 3a
= 8T(n - 3) + 4a + 2a + a
:
= 2kT(n - k) + (2k - 1)a
On Substituting Limiting Condition
T(1) = 1 ⇒ n - k = 1 ⇒ k = n - 1
Therefore, our solution becomes
(2n-1 + (2n-1 - 1)a = O(2n)
Q36: Let A[1,..., n] be an array storing a bit (1 or 0) at each location, and f(m) is a function whose Asymptotic Notation is θ(m). Consider the following program fragment written in a C like language: 
The complexity of this program fragment is (2004)
(a) Ω(π2)
(b) Ω(nlogn) and O(n2)
(c) θ(n)
(d) o(n)
Ans: (c)
Sol: The key part in the code is "counter = 0" in the else part as we can see below.
Lets take the best case. This happens when a[i] = 1 for all i, and then the loop executes with time complexity Θ(1) for each iteration and hence overall time complexity of Θ(n) and we can say time complexity of the code fragment is ()and hence options A and B are false.
Now, consider the worst case. This happens when a[i] = 0 or when else part is executed. Here, the time complexity of each iteration will be Θ(counter) and after each else, counter is reset to 0. Let k iterations go to the else part during the worst case. Then the worst case time complexity will be
Θ(x1) + Θ(x2) + ...+ Θ(xk) + Θ(n - k) where, xi is the value of the counter A(i) = 0 and f counter is called. but due to counter = 0
after each call to f(), we have,
x1 + x2 + ... xk = n - k. (counter is incremented n - k by the "if" part)
⇒ Θ(x1) + Θ(x2) +...+ Θ(xk) + Θ(n − k) =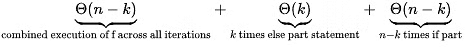
= Θ(k) + Θ(n – k) = Θ(n).
Since the time complexity is Ω(n) and Θ(n) we can say it is Θ(n)- Option (C).
(Option D is false because the small o needs the growth rate to be STRICTLY lower and not equal to or lower as the case for big O)
If counter = 0 was not there in else part, then time complexity would be Ω(n) and O(n2) as in worst case we can have equal number of 0's and 1's in array a giving time complexity
Θ(1) + Θ(2) + ... + Θ(n/2) would give O(n2)
Q37: The cube root of a natural number n is defined as the largest natural number m such that m3 ≤ n.
The complexity of computing the cube root of n(n is represented in binary notation) is (2003)
(a) O(n) but not O(n0.5)
(b) O(n0.5) but not O((log n)K) for any constant k > 0
(c) O((log n)k) for some constant k > 0, but not O((log log n)m) for any constant m > 0
(d) O((log log n)k) for some constant k > 0.5, but not O((log log n) 0.5)
Ans: (c)
Sol: We can simply do a binary search in the array of natural numbers from 1 .. n and check if the cube of the number matches n (i.e., check if 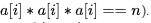 This check takes O(log n) time and in the worst case we need to do the search O(log n) times.
This check takes O(log n) time and in the worst case we need to do the search O(log n) times.
So, in this way we can find the cube root in O(log2 n). So, options (A) and (B) are wrong.
Now, a number is represented in binary using log n bit. Since each bit is important in finding the cube root, any cube root finding algorithm must examine each bit at least once. This ensures that complexity of cube root finding algorithm cannot be lower than log n.
(It must be Ω(log n)). So, (D) is also false and (C) is the correct answer.
Q38: Consider the following three claims
1. (n + k)m = Θ(nm), where k and m are constants
2. (2n+1 = O(2n)
3. 22n+1 = O(2n)
Which of these claims are correct? (2003)
(a) 1 and 2
(b) 1 and 3
(c) 2 and 3
(d) 1, 2 and 3
Ans: (a)
Sol: I. Rate of growth of (n + k)m is same as that of (nm) as k and m are constants.
(If either k or m is a variable then the equality does not hold), i.e., for sufficiently large values of n,
(n + k)m ≤ anm and
nm ≤ b(n + k)m
where a and b are positive constants. Here, a can be km and b can be 1.
So, TRUE.
II. 2n+1 = 2 x (2n) = Θ (2n) as 2 is a constant here.
As 2 n+1 is both upper and lower bounded by 2n we can say 2n+1 = O(2n).(Θ implies both O as well as Ω)
So, TRUE.
III. 22n+1 has same rate of growth as 22n.
22n = 2n2 = 2n x 2n
2n is upper bounded by (2n)2, not the other way round as 22n is increasing by a factor of 2n which is not a constant.
So, FALSE.
Q39: Consider the following functions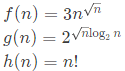
Which of the following is true? (2000)
(a) h(n) is O(f(n))
(b) h(n) is O(g(n))
(c) g(n) is not O(f(n))
(d) f(n) is O(g(n))|
Ans: (d)
Sol: 
Case of ℎ(n) is given only by an upper bound but factorial has higher growth rate than exponential.
f(n) and g(n)are having same order of growth as f(n) is simply 3 × g(n)(we can prove this by taking log also). So, (d) is correct and all other choices are false.
Q40: Let S be a sorted array of n integers. Let T(n) denote the time taken for the most efficient algorithm to determined if there are two elements with sum less than 1000 in S. Which of the following statement is true? (2000)
(a) T(n) is O(1)
(b) n ≤ T(n) ≤ n log2 n
(c) n log2 n ≤ T(n) < n/2
(d) T(n) = (n/2)
Ans: (a)
Sol: Answer: Option A. Because array is always sorted just check the 1st two elements.
Q41: If T1= O(1), give the correct matching for the following pairs: (1999)
(a) M-W, N-V, O-U, P-X
(b) M-W, N-U, O-X, P-V
(c) M-V, N-W, O-X, P-U
(d) M-W, N-U, O-V, P-X
Ans: (d)
Sol: (M) T(n) = Sum of first n natural numbers =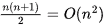
(N) T(n) = Θ(n) = O(n), third case of Master theorem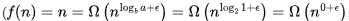 satisfied for any positive ∈ ≤ 1
satisfied for any positive ∈ ≤ 1
Also,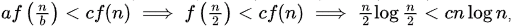 satisfied for c = 0.5)
satisfied for c = 0.5)
(P) Like in (M), here we are adding the log of the first n natural numbers. So,
Tn = log 1 + log 2 + log 3 +...+ log n
= log(1 x 2 x ... x n)
= log(n!)
= Θ(n log n) (Stirling's Approximation)
Q42. Let T(n) be the function defined by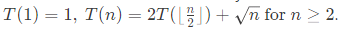
Which of the following statements is true? (1997)
(a) T(n) = O√n
(b) T(n)=O(n)
(c) T(n) = O(log n)
(d) None of the above
Ans: (b)
Sol: using master method (case 1)
where a = 2, b = 2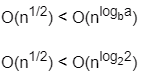
Q43: Which of the following is false? (1996)
(a)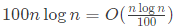
(b)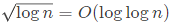
(c) If 0 < x < y then nx = O (ny)
(d) 2n ≠ O (nk)
Ans: (b)
Sol:
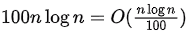 : Big-O denotes the growth rate of functions and multiplication or division by a constant does not change the growth rate. So, this is TRUE and here O can even be replaced by Θ or Ω.
: Big-O denotes the growth rate of functions and multiplication or division by a constant does not change the growth rate. So, this is TRUE and here O can even be replaced by Θ or Ω.- √log n = O (log log n) : FALSE: √log n = (log n)0.5grows faster than log log n as any positive polynomial function (including powers between 0−1) grows faster than any polylogarithmic function. (Ref: Section 3.2- Logarithms, Cormen). We can also do substitution here, but we must do for at least 2 large values and ensure it works for any larger n also.
- 0 < x < y the nx = O(ny): TRUE since y is always greater than x . So, RHS is always greater than LHS.
- 2n ≠ O(nk) : TRUE since k is constant. So, for large values of n, LHS is much higher than RHS (exponential function always greater than linear).
Only B is FALSE.
Q44: Consider the following two functions: (1994)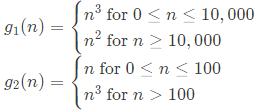
Which of the following is true?
(a) g1(n) is O(g2(n))
(b) g1(n) is O(n3 )
(c) g2(n) is O(g1 (n))
(d) g2(n) is O(n)
Ans: (a, b)
Sol: For asymptotic complexity, we assume sufficiently large n. So, g1(n) = n2 and g2(n) = n3
Growth rate of g1 is less than that of g2, i.e., g1 (n) = O(g2(n)).
Option A and B are TRUE here.
Q45: ∑1≤k≤n O(n), where O(n) stands for order n is: (1993)
(a) O(n)
(b) O(n2)
(c) O(n3)
(d) O(3n2)
(e) O(1.5n2)
Ans: (b, c, d, and e)
Sol: This is N added itself N times. So it is N2. Even if you consider as sum of
O(1) + O(2) +...+ O(n - 1) + O(N). it will add up to N2
So, the answer is:
(A) O (N) this is false.
(B, C, D, E) All of this is true. We have N2 here, so all options apart from (A) are correct.
In fact B = D = E this three options are same. and N3 is always the upper bound of N2. So O(N3) is also true.
PS: ∑(k = 1 to n) O(K) is never equal to n functions. It is always equal to one single function.
It can be written as c.1 + c.2 + c.3 and so on which results in O(N2) (source Cormen)
Q46: Let f (n) = n2logn and g(n) = n(logn)10 be two positive functions of n. Which of the following statements is correct ?(2001)
(a) f (n) = O(g(n)) and g(n) ≠ O(f (n))
(b) g(n) = O(f (n)) and f (n) ≠ O(g(n))
(c) f (n) ≠ O(g(n)) and g(n) ≠ O(f (n))
(d) f (n) = O(g(n)) and g(n) = O(f (n))
Ans: (b)
Sol: A more formal approach:
f(n) = n2 log n
g(n)= n(log n)10
We can use the limit definition of O-notation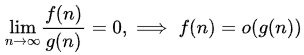
small o implying f is strictly asymptotically lower than g. Also by definition, o ⇒ O but 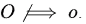
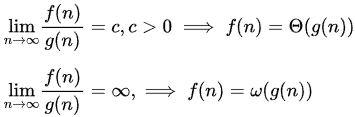
small ω implying f is strictly asymptotically higher than g. Also by definition, ω ⟹ Ω, but Ω  ω.
ω.
We can use this to prove the above question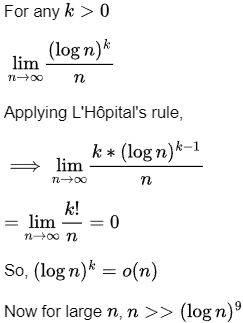
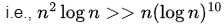 (Multiplying both sides by n log n)
(Multiplying both sides by n log n)
So, 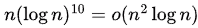 and
and 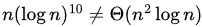 (making LHS strictly asymptotically lower than RHS)
(making LHS strictly asymptotically lower than RHS)
Or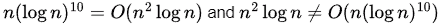
|
81 videos|113 docs|34 tests
|
FAQs on Previous Year Questions: Asymptotic Notation - Algorithms - Computer Science Engineering (CSE)
| 1. What is the purpose of using asymptotic notation in algorithm analysis? |  |
| 2. How is Big O notation different from Omega notation in asymptotic analysis? |  |
| 3. Can asymptotic notation be used to compare algorithms with different input sizes? |  |
| 4. How does Theta notation differ from Big O notation in asymptotic analysis? |  |
| 5. Why is it important to understand asymptotic notation in algorithm analysis? |  |
















