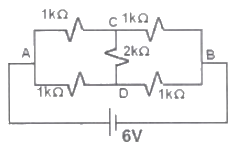
Q31: The current through the 2 kΩ resistance in the circuit shown is (2009)
(a) 0 mA
(b) 1 mA
(c) 2 mA
(d) 6 mA
Ans: (a)
Sol: Bridge is balanced i.i. node C and node D are at same potential. Therefore, no current flows through 2kΩ resistor.
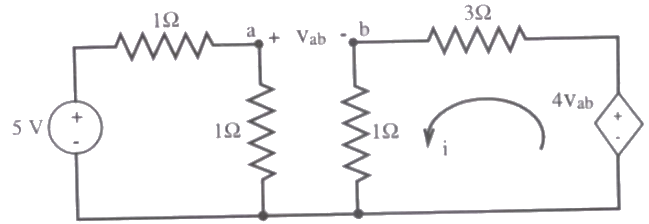
Q32: In the circuit shown in the figure, the value of the current i will be given by (2008)
(a) 0.31 A
(b) 1.25 A
(c) 1.75 A
(d) 2.5 A
Ans: (b)
Sol: 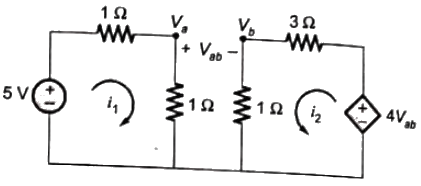By KVL in loop-1,
By KVL in loop-2,
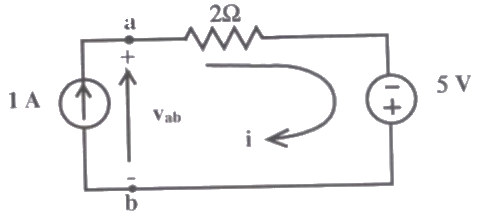
Q33: Assuming ideal elements in the circuit shown below, the voltage Vab will be (2008)
(a) -3 V
(b) 0 V
(c) 3 V
(d) 5 V
Ans: (a)
Sol: i = 1A
Applying KVL,
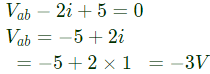NOTE: KVL is based on the conservation of energy.
Q34: A 3 V DC supply with an internal resistance of 2 Ω supplies a passive non-linear resistance characterized by the relation 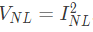. The power dissipated in the non linear resistance is (2007)
(a) 1.0 W
(b) 1.5 W
(c) 2.5 W
(d) 3.0 W
Ans: (a)
Sol: 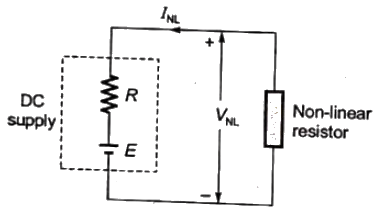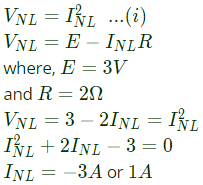-3 A is rejected, because the non-linear resistor is passive and the only active element in the circuit is 3 V DC supply. Which is supplying the power to the resistor.
So, INL= 1A
Power dissipated in the non-linear resistor
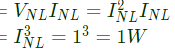
Q35: In the figure given below the value of R is (2005)
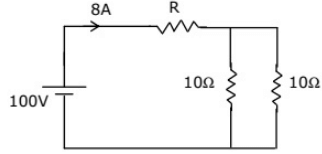(a) 2.5 Ω
(b) 5.0 Ω
(c) 7.5 Ω
(d) 10.0 Ω
Ans: (c)
Sol: The resultant (R) when viewed from voltage source = 100/8 = 12.5
Q36: The rms value of the resultant current in a wire which carries a dc current of 10 A and a sinusoidal alternating current of peak value 20 A is (2004)
(a) 14.1 A
(b) 17.3 A
(c) 22.4 A
(d) 30.0 A
Ans: (b)
Sol: R.M.S value of d.c current = 10A = Idc
R.M.S. value of sinusoidal current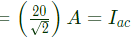
R.M.S. value of resultant,
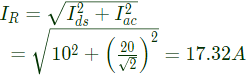
Q37: In figure, the value of resistance R in Ω is (2004)
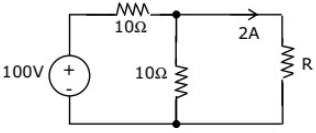(a) 10
(b) 20
(c) 30
(d) 40
Ans: (b)
Sol: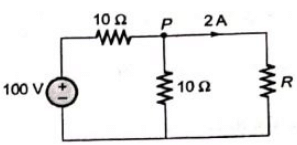
Q38: In figure, Ra, Rb and Rc are 20Ω, 10Ω and 10Ω respectively. The resistances R1, R2 and R3 in Ω of an equivalent star-connection are (2004)
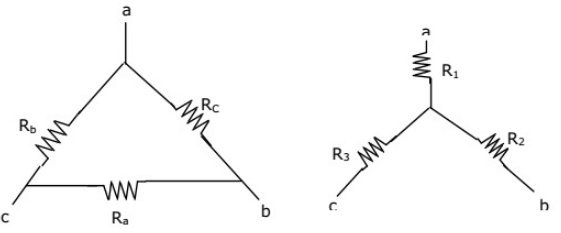(a) 2.5, 5, 5
(b) 5, 2.5, 5
(c) 5, 5, 2.5
(d) 2.5, 5, 2.5
Ans: (a)
Sol:
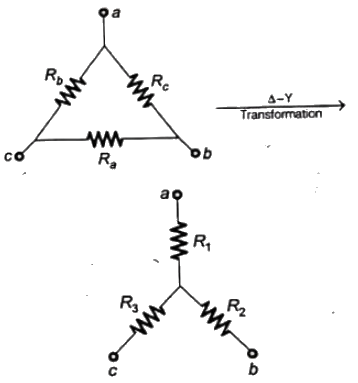
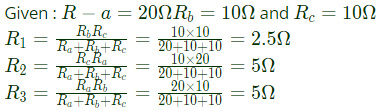Remember: If all the branches of Δ-connection has same impedance Z, then impedance of branch of Y-connection be Z/3.
Q39: In figure, the value of the source voltage is (2004)
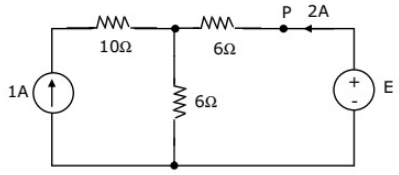(a) 12 V
(b) 24 V
(c) 30 V
(d) 44 V
Ans: (c)
Sol: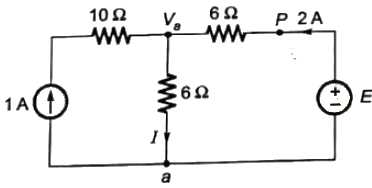
Method-1:
Using KCL,
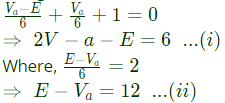Solving equation (i) and (ii), we get
Va = 18V and E = 30V
Method-2:
I = 2+1 = 3A
Applying KVL in second loop,
E = 2 x 6 + 3 x 6 = 30V
Q40: In figure, the value of R is (2003)
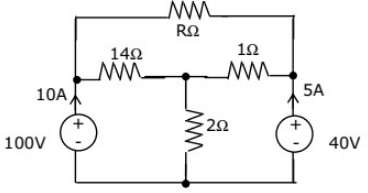(a) 10 Ω
(b) 18 Ω
(c) 24 Ω
(d) 12 Ω
Ans: (d)
Sol: By KCL,
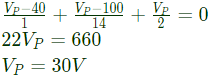
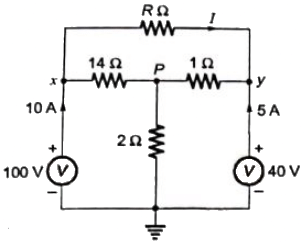Potential difference between node x and y = 60V
By taking KCL at node y
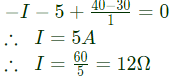
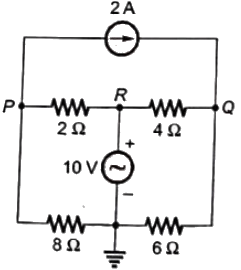
Q41: In figure, the potential difference between points P and Q is (2003)
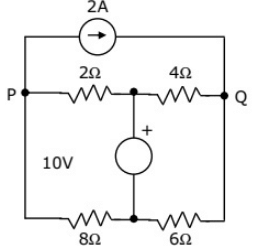(a) 12 V
(b) 10 V
(c) -6 V
(d) 8 V
Ans: (c)
Sol: 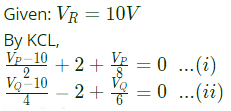From equation (i),
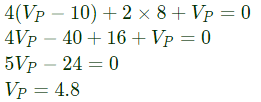From equation (ii),
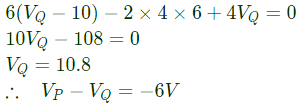
Q42: A segment of a circuit is shown in figure. VR = 5V, VC = 4sin2t. The voltage VL is given by (2003)
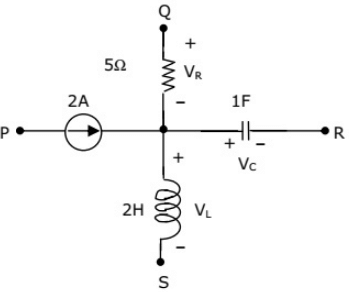(a) 3 - 8 cos 2t
(b) 32 sin 2t
(c) 16 sin 2t
(d) 16 cos 2t
Ans: (b)
Sol: By KCL,
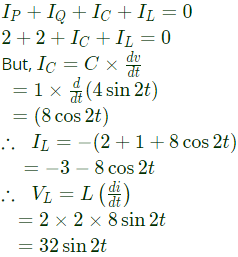NOTE: KCL is based on the law of conservation of charges.
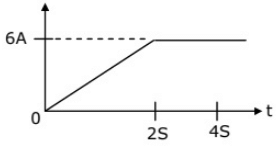
Q43: Figure Shows the waveform of the current passing through an inductor of resistance 1Ω and inductance 2 H. The energy absorbed by the inductor in the first four seconds is (2003)
(a) 144 j
(b) 98 j
(c) 132 j
(d) 168 j
Ans: (c)
Sol: For 0 < t < 2s current varies linearly with time and given as i(t) = 3t and for 2s < t < 4s current is constant, i(t) = 6A.
The energy absorbed by the inductor (Resistance neglected) in the first 2 sec,
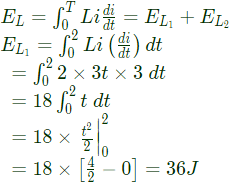The energy absorbed by the inductor in (2 → 4) second
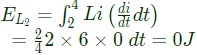A pure indictor does not dissipate enegy but only stores it. Due to resistance, some energy is dissipated in the resistor. Therefore, total energy stored in the inductor and the energy dissipated in the resistor.
The energy dissipated by the resistance in 4 sec.
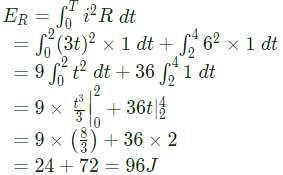The total energy absorbed by the inductor in 4 sec
= 96J + 36J = 132J
Q44: Consider the star network shown in figure. The resistance between terminals A and B with terminal C open is 6Ω, between terminals B and C with terminal A open is 11Ω, and between terminals C and A with terminal B open is 9Ω. Then (2001)
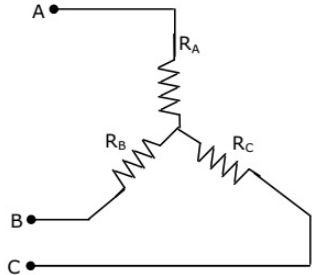(a) RA = 4Ω, RB = 2Ω, RC = 5Ω
(b) RA = 2Ω, RB = 4Ω, RC = 7Ω
(c) RA = 3Ω, RB = 3Ω, RC = 4Ω
(d) RA = 5Ω, RB = 1Ω, RC = 10Ω
Ans: (b)
Sol: When C is open,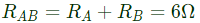
When B is open,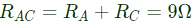
When A is open,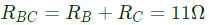
On solving the above equations
Q45: Two incandescent light bulbs of 40 W and 60 W rating are connected in series across the mains. Then (2001)
(a) the bulbs together consume 100 W
(b) the bulbs together consume 50W
(c) the 60 W bulb glows brighter
(d) the 40 W bulb glows brighter
Ans: (d)
Sol: 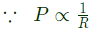Therefore , resistance of 40 W bulb > resistance of 60 W bulb.
For series connection, current through both the bulbs will be same P = I2R (for series connection).
Power consumed by 40 W bulb > Power consumed by 60 W bulb.
Hence the 40 W bulb glows brighter.
(a) 0 mA
(a) 0.31 A
By KVL in loop-1,
By KVL in loop-2,
(a) -3 V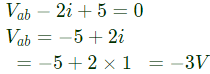
NOTE: KVL is based on the conservation of energy.
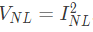. The power dissipated in the non linear resistance is (2007)
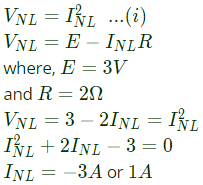-3 A is rejected, because the non-linear resistor is passive and the only active element in the circuit is 3 V DC supply. Which is supplying the power to the resistor.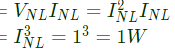
(a) 2.5 Ω
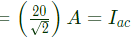
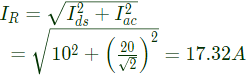
(a) 10
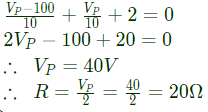
(a) 2.5, 5, 5
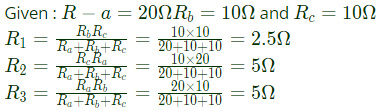Remember: If all the branches of Δ-connection has same impedance Z, then impedance of branch of Y-connection be Z/3.
(a) 12 V
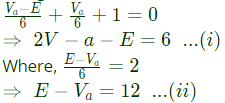Solving equation (i) and (ii), we get
(a) 10 Ω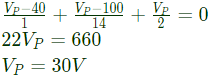
Potential difference between node x and y = 60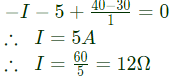V
(a) 12 V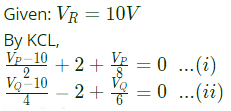
From equation (i),
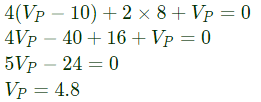From equation (ii),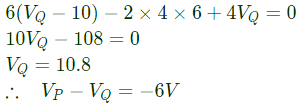
(a) 3 - 8 cos 2t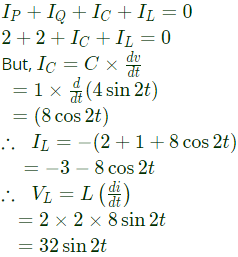
NOTE: KCL is based on the law of conservation of charges.
(a) 144 j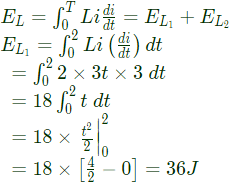
The energy absorbed by the inductor in (2 → 4) second
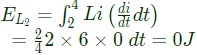A pure indictor does not dissipate enegy but only stores it. Due to resistance, some energy is dissipated in the resistor. Therefore, total energy stored in the inductor and the energy dissipated in the resistor.
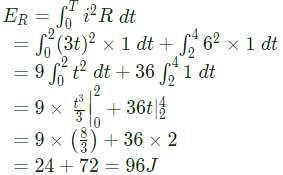The total energy absorbed by the inductor in 4 sec
(a) RA = 4Ω, RB = 2Ω, RC = 5Ω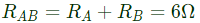
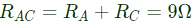
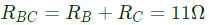
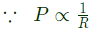Therefore , resistance of 40 W bulb > resistance of 60 W bulb.
