Previous Year Questions: Binary Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Q1: Consider the C function foo and the binary tree shown. (2023)
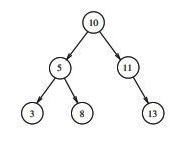
When foo is called with a pointer to the root node of the given binary tree, what will it print?
(a) 3 8 5 13 11 10
(b) 3 5 8 10 11 13
(c) 3 8 16 13 24 50
(d) 3 16 8 50 24 13
Ans: (c)
Sol: Given that ret v a l = p → v al + foo(p → left) + foo(p → right)
Means it will print the sum of ( value + left subtree whole value + right subtree whole value ).
Note that, until the child nodes completes the calculation, parent node calculation step will not complete.
Therefore leaf nodes returns the value of leaf nodes alone. ( 3 node, 8 node and 13 node will return 3, 8 and 13 respectively )
5 node will return 5+3+8 = 16
11 node will return 11+13 = 24
10 node will return 10+16+24 = 50
So sequence 3,8,16,13,24,50 only possible in the given options
As we know, there’s no rule about evaluation order of parameters of ‘+’
possible outcomes :
1. 3,8,16,13,24,50
2. 8,3,16,13,24,50
3. 13,24,3,8,16,50
4. 13,24,8,3,16,50
Q2: Consider a complete binary tree with 7 nodes. Let A denote the set of first 3 elements obtained by performing Breadth-First Search (BFS) starting from the root. Let B denote the set of first 3 elements obtained by performing Depth-First Search (DFS) starting from the root. The value of |A-B| is _____________ (2021 SET 2)
(a) 3
(b) 4
(c) 1
(d) 2
Ans: (c)
Sol: Complete binary tree property has this property that every level until last is fully filled and last level is filled from left to right.
So, when we have a complete binary tree with 7 nodes,
level 1 has 1 node ( root )
level 2 has 2 nodes.
level 3 has 4 nodes.
BFS goes level by level. So first three elements (say Set A) level 1 nodes (1) + level 2 (2)
DFS is go by connected manner. So first three elements (say Set B ) level 1 nodes (1) + one node from level 2 nodes + one nodes
level 3 nodes which is connected to the previously chosen level 2 node.
A- B = the remaining node from the set of level 2 nodes.
⇒|A-B| =1.
Q3: Let T be a full binary tree with 8 leaves. (A full binary tree has every level full.) Suppose two leaves a and b of T are chosen uniformly and independently at random. The expected value of the distance between a and b in T (i.e., the number of edges in the unique path between a and b) is (rounded off to 2 decimal places) ___________. (2019)
(a) 2.5
(b) 4.25
(c) 6.5
(d) 3.75
Ans: (b)
Sol: See the word "independently" here. It means that choice of a must not affect choice of band vice versa. This implies that both a and b can even be the same node.
- Now, we are given that the binary tree has 8 leaves. (2 ³ =8) ⟹ we have 3 levels in the tree starting from 0. The distance in terms of number of edges between any two leaf nodes will always be even. If we consider any two leaves (not necessarily distinct)
No. of pairs with path length 0 = 8 (When a = b) - No. of pairs with path length 2=8.(For each of the 8 leaf nodes, we have a pair and since the selection is independent order of the pair is also significant)
- No. of pairs with path length 4 =16. (For each leaf node we have to go two levels up and while coming down we have 2 choices. So, we get
- 8 x 2 = 16pairs)
- No. of pairs with path length 6 =32. (For each leaf node we have to go till the root, and from there while coming down it has 2 x 2 = 4 choices. Thus we get 8x4= 32 pairs. Total number of possible pairs =8 x 8 =64
- So, expected path length
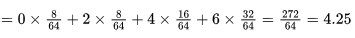
Q4: The post traversal of a binary tree is 8,9,6,7,4,5,2,3,1. The in order traversal of the same tree is 8,6,9,4,7,2,5,1,3. The height of a tree is the length of the longest path from the root to any leaf. The height of the binary tree above is ______. (2018)
(a) 4
(b) 5
(c) 3
(d) 6
Ans: (a)
Sol:
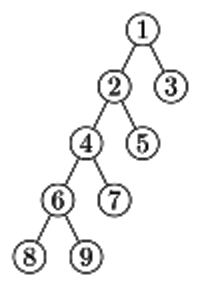
Nodes in longest path from Root to Leaf
=(1-2,2-4,4-6,6-8) or ( 1-2,2-4,4-6,6-9)
|Longest Path|(1 -2,2-4,4-6,6-8)
Q5: Consider the following New-order strategy for traversing a binary tree: (2016 SET 2)
Visit the root;
Visit the right sub tree using New-order;
Visit the left sub tree using New-order;
The New-order traversal of the expression tree corresponding to the reverse polish expression 3 4 * 5 - 2 ^ 6 7 * 1 + - is given by:
(a) + -167*2^5-34*
(b) - +1*67^2-5*34
(c) - +1*76^2-5*43
(d) 1 76*+2543*-^-
Ans: (c)
Sol: Expression given in reverse polish notation (i,e in Post-order) convert first it into In-order
34 *5-2 ∧67*1+-
(3 *4) 5-2 ∧67*1+-
((3*4)-5 )2 ∧ 67*1+-
(((3*4)-5) ∧2)67*1+-
(((3*4)-5)^2) (6*7) 1+-
(((3*4)-5)^2) ((6*7) +1) -
((((3 *4)-5)^2) - ((6*7) + 1))
so In order expression in (((( 3*4 -5)∧2)-((6*7)+1))
New-Order traversal is as by ROOT RIGHT LEFT
((((3+4)-5)^2) - ((6*7) + 1)) -
-((6*7)+1)(((3*4) -5)^2)
-+1(6*7) (((3+4)-5)∧2)
-+1*76(((3*4)-5)^2)
+1*76∧2((3*4)-5)
-+1*76 ∧2-5(3 *4)
-+1*76∧2-5*43
Q6: Consider a binary tree T that has 200 leaf nodes. Then, the number of nodes in T that have exactly two children are ________. (2015 SET 3)
(a) 99
(b) 100
(c) 199
(d) 149
Ans: (c)
Sol: Let number of nodes with exactly two children be x, and with exactly one children be y.
Total degree = 200 + 3 x + 2 y − 1 (As all nodes with 2 children have degree 3 except the root)
No. of nodes = x + y + 200
No. of edges = Total degree/ 2 = ( 200 + 3 x + 2 y − 1 ) / 2 [Handshaking Theorem]
No. of edges in a tree = No. of nodes − 1,
So, (200+3x+2y−1)=2x+2y+400−2
x=199
Q7: A binary tree T has 20 leaves. The number of nodes in T having two children is _______. (2015 SET 2)
(a) 20
(b) 19
(c) 39
(d) 9
Ans: (b)
Sol: Let l be the number of leaf nodes, D1 be the number of nodes with one child and D2 be the number of nodes with two children.
Sum of Degrees , D = I × l + 3 × D 2 + 2 × D 1 − 1 (for root)
(Root is having one degree less because it is not having a parent)
D = l + 3 D 2 + 2 D 1 − 1 → ( 1 )
Number of edges , e =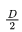
Number of nodes , n = D 2 + D 1 + l
A tree with n nodes has n − 1 edges so,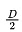 = D 2 + D 1 + l − 1 → ( 2 )
= D 2 + D 1 + l − 1 → ( 2 )
From ( 1 ) and ( 2 )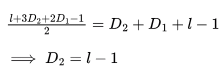
So, the number of nodes in T having two children =20-1 =19
Q8: The height of a tree is the length of the longest root-to-leaf path in it. The maximum and minimum number of nodes in a binary tree of height 5 are (2015 SET 1)
(a) 63 and 6, respectively
(b) 64 and 5, respectively
(c) 32 and 6, respectively
(d) 31 and 5, respectively
Ans: (a)
Sol: Option A is correct because height 5 means level 6 so maximum node =2I-1=26-1= 63 and for minimum, at each level only single node so total 6.
Q9: Consider the pseudocode given below. The function Do something () takes as argument a pointer to the root of an arbitrary tree represented by the left Most Child-right Sibling representation. Each node of the tree is of type tree Node. (2014 SET 3)

When the pointer to the root of a tree is passed as the argument to DoSomething, the value returned by the function corresponds to the
(a) number of internal nodes in the tree
(b) height of the tree
(c) number of nodes without a right sibling in the tree.
(d) number of leaf nodes in the tree.
Ans: (d)
Sol: Here, the condition for count value =1 is
if (tree → left Most child ==Null
- so, if there is no left-most child of the tree (or the sub-tree or the current node called in recursion)
- Which means there is no child to that particular node (since if there is no left-most child, there is no child at all as per the tree representation given).
- ∴ the node under consideration is a leaf node.
The function recursively counts, and adds to value, whenever a leaf node is encountered.
Q10: Consider the expression tree shown. Each leaf represents a numerical value, which can either be 0 or 1. Over all possible choices of the values at the leaves, the maximum possible value of the expression represented by the tree is ___. (2014 SET 2)
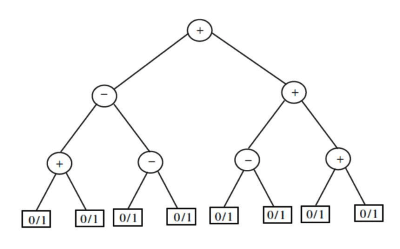 (a) 5
(a) 5
(b) 6
(c) 7
(d) 8
Ans: (b)
Sol: 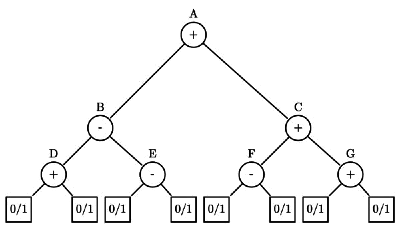 A = B + C
A = B + C
For A to be maximum, both B and C should be maximum
B = D − E
For B to be maximum, D should be maximum
and E should be minimum
For C to be maximum both F and G should be maximum,
The maximum value of D is 2 ( 1 + 1 = 2 )
The minimum value of E is − 1 ( 0 − 1 = − 1 )
The maximum value of F is 1 ( 1 − 0 = 1 )
The maximum value of G is 2 ( 1 + 1 = 2 )
B = 2 − ( − 1 ) = 2 + 1 = 3 C = 1 + 2 = 3
C=1+2=3
A=B+C=3+3=6
Q11: Consider rooted n node binary tree represented using pointers. The best upper bound on the time required to determine the number of sub trees having exactly 4 nodes is O(n a lob b n). Then the value of a+10b is_______ (2014 SET 1)
(a) 1
(b) 11
(c) 10
(d) 21
Ans: (a)
Sol:
1. Come to the 4thlevel up from the leaf node of the given binary tree, which can be done using tree traversal in O ( n ).
2. For each node present in the level check whether it's subtree having exactly 4 nodes.. which can be done in constant time for each node, since it's subtree having constant number of nodes..
3. nodes in the level is less than n.. so its complexity is O ( n )
Therefore, a = 1 and b=0
Q12: The height of a tree is defined as the number of edges on the longest path in the tree. The function shown in the pseudocode below is invoked as height(root) to compute the height of a binary tree rooted at the tree pointer root. (2012)
The appropriate expressions for the two boxes B1 and B2 are
(a) B1: (1+height(n → right))
B2: (1+max(h1, h2))
(b) B1: (height(n → right))
B2: (1+max(h1,h2))
(c) B1: height(n → right)
B2: max(h1, h2)
(d) B1: (1+ height(n → right))
B2: max(h1, h2)
Ans: (a)
Sol:
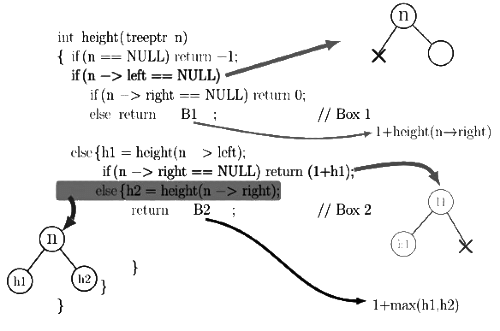
Q13: In a binary tree with n nodes, every node has an odd number of descendants. Every node is considered to be its own descendant. What is the number of nodes in the tree that have exactly one child? (2010)
(a) 0
(b) 1
(c) (n-1)/2
(d) n-1
Ans: (a)
Sol: 0 because every node has an odd number of descendants so least odd number 1 and every node is considered to be its own descendant so all nodes have even number of descendants ( 0 , 2 , 4 , 6. . . ) so every node has either 0 children or 2 children...
Q14: A binary tree with n>1 nodes has n1,n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors. Starting with the above tree, while there remains a node v of degree two in the tree, add an edge between the two neighbors of v and then remove v from the tree. How many edges will remain at the end of the process? (2008)
(a) 2*n1-3
(b) n2 +2∗ n1-2
(c) n3- n2
(d) n2+n1
Ans: (a)
Sol: Initially, n 1 ∗ 1 + n 2 ∗ 2 + n 3 ∗ 3 = 2 ( n 1 + n 2 + n 3 − 1 ) ⟹ n 3 = n 1 − 2
Now we have removed all 2 degree nodes, so number of edges in final graph is
n 1 + n 3 − 1.
Put n 3 = n 1 − 2 , we get
Number of edges=2*n1-3
Q15: A binary tree with n>1 nodes has n1,n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors. (2008)
n3 can be expressed as
(a) n1+ n2 -1
(b) n1-2
(c) [(( n1 +n2/2))]
(d) n2-1
Ans: (b)
Sol: Given definition of degree: no of neigh bourse of a node.
total nodes =n=n1+n2 +n3
Apply handshaking lemma:
Sum of degrees =2*no of edges
1*n1+ 2* n2 +3* n3 =2(n-1)
Total number of edges in graph will always be (n1+n2 +n3.-1)
1*n1+ 2* n2 +3* n3 =2(n-1) =2 (n1+n2 +n3.-1)
Q16: The following three are known to be the preorder, in order and post order sequences of a binary tree. But it is not known which is which. (2008)
I.MBCAFHPYK
II.KAMCBYPFH
III.MABCKYFPH
Pick the true statement from the following.
(a) I and II are preorder and in order sequences, respectively
(b) I and III are preorder and post order sequences, respectively
(c) II is the in order sequence, but nothing more can be said about the other two sequences
(d) II and III are the preorder and in order sequences, respectively
Ans: (d)
Sol: In preorder, root comes at the beginning of the traversal sequence and in post order, root comes at the last of the traversal sequence. So, out of the given sequences only 1 and 2 are having such kind of order I. e K at the beginning and at the last.
Therefore, 2 is the preorder and 1 is post order and the left sequence I .e 3 will definitely be in order.
Q17: Consider the following C program segment where Cell Node represents a node in a binary tree: (2007)

The value returned by Get Value when a pointer to the root of a binary tree is passed as its argument is:
(a) the number of nodes in the tree
(b) the number of internal nodes in the tree
(c) the number of leaf nodes in the tree
(d) the height of the tree
Ans: (c)
Sol: As the function returns 1 if and only if any node has both left & right children as N U L L
(that node is a leaf node). Hence, value gets incremented at each leaf node
Q18:The in order and preorder traversal of a binary tree are d b e a f c g and a b d e c f g, respectively The post order traversal of the binary tree is: (2007)
(a) d e b f g c a
(b) e d b g f c a
(c) e d b f g c a
(d) d e f g b c a
Ans: (a)
Sol: Take the first node in preorder traversal - a will be the root of the tree All nodes to the left of ' a ' in in order traversal will be in the left subtree of ' a ' and all elements on the right will be in the right subtree of ' a '.
Take the second element from preorder traversal - ' b ' - goes to left subtree of ' a ' as it is in the left of ' a ' in in order list.
Proceeding likewise we can construct the binary tree as:
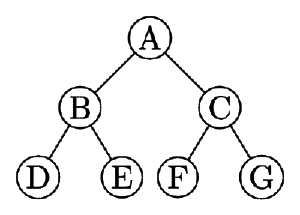 Q19: The maximum number of binary trees that can be formed with three unlabeled nodes is: (2007)
Q19: The maximum number of binary trees that can be formed with three unlabeled nodes is: (2007)
(a) 1
(b) 5
(c) 4
(d) 3
Ans: (b)
Sol: Can be found with formula... ( 2 n C n / n + 1 )..n being the number of nodes. for the given question...where n = 3...answer is 5 . Let me also specify here.. that number of Binary Search Trees with n nodes is equal to number of unlabeled Binary trees.
Q20: The height of a binary tree is the maximum number of edges in any root to leaf path. The maximum number of nodes in a binary tree of height h is: (2007)
(a) 2h-1
(b) 2h1-1
(c) 2h1-1
(d) 2h+1
Ans:(c)
Sol: 2h-1 just try this taking a small complete binary
never try to remember these formulae as remembering formulae is an overhead try to take examples in such cases
Q21: An array X of n distinct integers is interpreted as a complete binary tree. The index of the first element of the array is 0. If the root node is at level 0, the level of element X[ i] ,i≠0, is (2006)
(a) [log 2i]
(b) [log 2(i =1)]
(c) [log 2(i =1)]
(d) [log 2i]
Ans: (c)
Sol: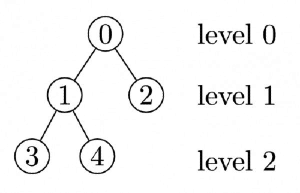 PS : the value inside the node is array index
PS : the value inside the node is array index
A False , [log 2i] =[log 21] =0 But X[ 1] is at level 1
B False , [log 2(i =1)]= [log 2(4+1)] [log 2(5)] =3but X[4] is at level 2
D False, [log 2i] =[log 21 =0 But X[ 1] is at level 1
Q22: An array X of n distinct integers is interpreted as a complete binary tree. The index of the first element of the array is 0. If only the root node does not satisfy the heap property, the algorithm to convert the complete binary tree into a heap has the best asymptotic time complexity of (2006)
(a) O(n)
(b) O(log n)
(c) O(n log n)
(d) O(n log log n)
Ans: (b)
Sol: Here we need to call Heap / Bubble down/ Percolate down procedure on Root, which in the worst case will take time O(log n) . So B is the correct option.
Other options do not even make sense, because with O(n) we can even build an entire Heap not just heap on the root. O(n log n) & O(n log log n) is more than O(n) .
Q23: An array X of n distinct integers is interpreted as a complete binary tree. The index of the first element of the array is 0. The index of the parent of element X[ i] ,i≠0, is (2006)
(a) [ i/2]
(b) [ i-1/2]
(c) [ i/2]
(d) [ i/2]-1
Ans: (d)
Sol: Left child of the element will be at 2 ∗ i + 1 and right child at 2 (i +1)
Q24: In a binary tree, the number of internal nodes of degree 1 is 5, and the number of internal nodes of degree 2 is 10. The number of leaf nodes in the binary tree is (2006)
(a) 10
(b) 11
(c) 12
(d) 15
Ans: (b)
Sol: We are given no. of 1 degree node = 5 , no. of 2 degree nodes = 10 .
Total no. of edges = 1 ∗ 5 + 2 ∗ 10 = 25 (In tree degree is for outgoing edges only, and hence each degree corresponds to an edge)
So, total no. of nodes = 25 + 1 = 26 (No. of nodes in a tree is 1 more than no. of edges).
Now, no. of leaf nodes (nodes with 0 degree) = 26 − 5 − 10 = 11 .
Q25: A scheme for storing binary trees in an array X is as follows. Indexing of X starts at 1 instead of 0. The roots is stored at X[1]. For a node stored at X[i], the left child, if any, is stored in X[2i] and the right child, if any, in X[2i + 1]. To be able to store any binary tree on n vertices, the minimum size of X should be (2006)
(a) log n
(b) n
(c) 2n+1
(d) 2n-1
Ans: (d)
Sol: Any Binary Tree and Size should be minimum " .
⟹Minimum size of worst case binary tree
X [ i ] = n o d e X [ 2 i ] = Left child X [ 2 i + 1 ] = R i g h t c h i l d
Let n=3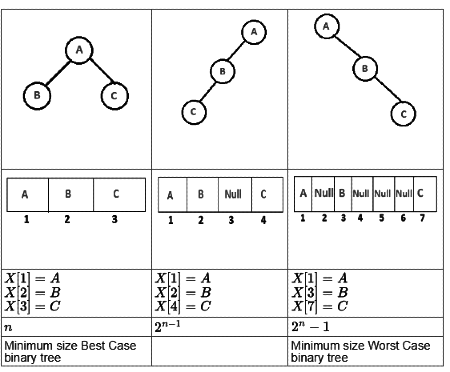
Q26: In a binary tree, for every node the difference between the number of nodes in the left and right subtrees is at most 2. If the height of the tree is h > 0, then the minimum number of nodes in the tree is (2005)
(a) 2h-1
(b) 2h-1+1
(c) h2-1-1
(d) 2h
Ans: (b)
Sol: Since the difference between the nodes in left and right subtree must hold for every node, until the last to last to last level, all levels must be fully filled. So, we get 2 h−1 − 1 nodes (No. of nodes in a complete binary tree of height h−2 ). Now, our aim is to increase two more levels by adding minimum no. of nodes- just add two in nodes one below other to any of the nodes. So, we get 2h−1 + 1 nodes.
Q27: Which one of the following binary trees has its in order and preorder traversals as BCAD and ABCD, respectively? (2004)
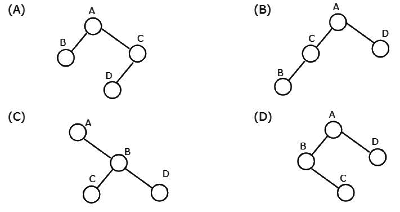
(a) A
(b) B
(c) C
(d) D
Ans: (d)
Sol: In order traversal is left node right.
Preorder is node left right
Q28: Consider the following C program segment (2004)
The value returned by the function DoSomething when a pointer to the root of a non-empty tree is passed as argument is
(a) The number of leaf nodes in the tree
(b) The number of nodes in the tree
(c) The number of internal nodes in the tree
(d) The height of the tree
Ans: (b)
Sol: It calculates Height of tree.
Easy way to get this answer .
Draw a tree where all 4 parameters are different.
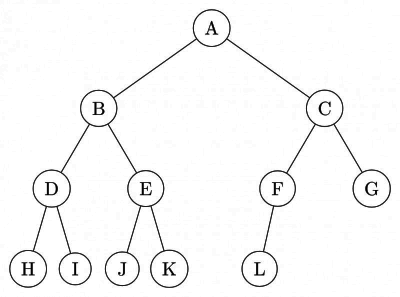
Q28: Consider the label sequences obtained by the following pairs of traversals on a labeled binary tree. Which of these pairs identify a tree uniquely? (2004)
(i) preorder and post order
(ii) in order and post order
(iii) preorder and in order
(iv) level order and post order
(a) (i) only
(b) (iii) only
(c) (iv) only
(d) (ii), (iii)
Ans: (d)
Sol: Following combination can uniquely identify a tree.
- In order and Preorder.
- In order and Post order.
- In order and Level-order.
- And following do not.
- Post order and Preorder.
- Preorder and Level-order.
- Post order and Level-order.
Q29: Level order traversal of a rooted tree can be done by starting from the root and performing (2004)
(a) preorder traversal
(b) in-order traversal
(c) depth first search
(d) breadth first search
Ans: (d)
Sol: Level order traversal of the tree resembles the Breadth-first search of the graph
Q30: Let LASTPOST, LASTIN and LASTPRE denote the last vertex visited `in a post order, in order and preorder traversal respectively, of a complete binary tree. Which of the following is always true? (2000)
(a) LASTIN = LASTPOST
(b) LASTIN = LASTPRE
(c) LASTPRE = LASTPOST
(d) None of the above
Ans: (d)
Sol: In order : Left → Root → Right
Preorder : Root → Left → Right
Post order: Left → Right → Root
If the binary tree is full (last level is fully filled), the last visited node in In order and Preorder must be the rightmost one in the last level. But for a complete binary tree this need not be the case (in a complete binary tree last level need not be fully filled) and LASTPRE will be from the second last level in case the complete binary tree is not full. So, choice (D).
Q31: Consider the following nested representation of binary trees: (XYZ)indicates Y and Z are the left and right subtrees, respectively, of node X. Note that Y and Z may be NULL, or further nested. Which of the following represents a valid binary tree? (2000)
(a) (1 2 (4 5 6 7))
(b) (1 (2 3 4) 5 6) 7)
(c) 3 4) (5 6 7))
(d) (1 (2 3 NULL) (4 5))
Ans: (c)
Sol:
A → ( 4 5 6 7 ) this part of answer is not correct. We have (XY Z) not ( WXYZ ) . So, this is wrong
B → 3 closing parentheses,2opening parentheses. This is wrong.
C CORRECT
D → Here in ( 1 ( 2 3 N U L L ) ( 4 5 ) ) , ( 4 5 ) this is not allowed. So this is wrong. (It should be ( 4 , 5 , N U L L ) )
Q32: Which of the following statements is false? (1998)
(a) A tree with a n nodes has (n- 1) edges
(b) A labeled rooted binary tree can be uniquely constructed given its post order and preorder traversal results.
(c) A complete binary tree with n internal nodes has (n + 1) leaves.
(d) The maximum number of nodes in a binary tree of height h is 2h+1-1
Ans: (c)
Sol: Tree with n nodes must have n−1 edges.
A labeled rooted binary tree can be uniquely constructed given its post order and preorder traversal results. (in order must be needed with either preorder or post order for that) A complete binary tree with n nodes can have n leaves also
Example:
Since: A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible. So false
The maximum number of nodes in a binary tree of height h is
1 + 2 + 4 + . . . . . + 2h= 2h+1−1 So true
Answer is b and c both.
Since, 2 answers are there I would choose b, because in some places by "complete" binary tree they mean "full binary tree" which has all the levels completely filled.
Q33: Which of the following sequences denotes the post order traversal sequence of the below tree? (1996)
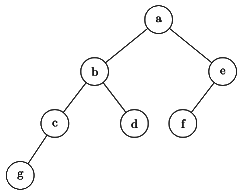
(a) fegcdba
(b) gcbdafe
(c) gcdbfea
(d) fedgcba
Ans: (c)
Sol: Post order: Left → Right → Root.
Root is at last. (here a) So option B eliminated.
g is leftmost node so it should be traversed first. So B and D eliminated.
Q34: A binary tree T has n leaf nodes. The number of nodes of degree 2 in T is (1995)
(a) log 2n
(b) n-1
(c) n
(d) 2n
Ans: (b)
Sol: In Binary Tree a node can have at most 2 children.
Total number of node N = node with 0 child + node with 1 child + node with 2 child.
⟹ N = n0+n1+n2 ( here, in question it is given that no. of leaf nodes i.e no. of nodes with
0children is n so n0=n )
⟹ N = n+n1+n2
Total number of edges e = N−1 , and also e = n ∗ 0 + n1∗1 + n2 ∗ 2
∴ N−1 = n ∗ 0 +n1 ∗1 + n2∗2
⟹ n+n1+n2−1 = n1 ∗1+n2 ∗ 2
⟹ n2=n−1
Q35: Which of the following statements is false? (1994)
(a) Optimal binary search tree construction can be performed efficiently using dynamic programming
(b) Breadth-first search cannot be used to find connected components of a graph
(c) Given the prefix and postfix walks over a binary tree, the binary tree cannot be uniquely constructed.
(d) Depth-first search can be used to find connected components of a graph
Ans: (b)
Sol:
A. An optimal binary search tree is a binary search tree for which the nodes are arranged on levels such that the tree cost is minimum and it can be performed efficiently using Dynamic programming.
B. To find Connected components we can start with either BFS or DFS but DFS is prefer over BFS because BFS takes exponential amount of memory whereas DFS takes linear amount of memory
C. Using prefix and postfix the binary tree cannot be uniquely constructed
D. It can be used and it consumes linear amount of memory
Q36: Choose the correct alternatives (More than one may be correct). The total external path length, EPL, of a binary tree with n external nodes is, Σw= Iw where Iw is the path length of external node w), (1990)
(a) ≤ n2always.
(b) ≥ n log2n always.
(c) Equal to n2 always.
(d) O(n) for some special trees
Ans: (d)
Sol: Here, n denotes the number of external (leaf) nodes and not the total number of nodes.
A. By adding an edge to the root of a skewed binary tree of say 10 nodes, we get a binary tree of 11 nodes having 2 external nodes of path lengths 9 and 1 respectively giving EPL = 9 + 1 = 10 > 22 . So, option A is false.
B. This is always TRUE. The minimum EPL for a given number of external nodes n happens for a full binary tree. In this case when we have n external nodes and (2n−1 ) total nodes and each external node will have a path length of log2 ( 2 n − 1 ) giving total external path length, EPL = n log2 ( 2n −1) . Now, if we try to add any amount of skewed to this full binary tree we can see that EPL > n log2 ( 2 n−1 ) .
C. False as shown for option A.
D. False as shown for option B.
Q37: Choose the correct alternatives (More than one may be correct). The number of rooted binary trees with n nodes is, (1990)
(a) Equal to the number of ways of multiplying (n+1) matrices.
(b) Equal to the number of ways of arranging n out of 2 n distinct elements
(c) Equal to 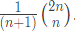
(d) Equal to n!
Ans: (a, c)
Sol: Number of rooted binary trees (unlabeled) with n nodes is given by nth Catalan number which equals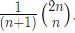 .
.
Here, both options A and C are true as option A corresponds to n multiply operations of n+1 matrices, the number of ways for this is again given by the nth Catalan number.
Q38: Answer the following: Which one of the following statements (s) is/are FALSE? (1989)
(a) Overlaying is used to run a program, which is longer than the address space of the computer.
(b) Optimal binary search tree construction can be performed efficiently by using dynamic programming.
(c) Depth first search cannot be used to find connected components of a graph.
(d) Given the prefix and postfix walls over a binary tree, the binary tree can be uniquely constructed
Ans: (a, c ,d )
Sol:
A. FALSE according to definition of address space given in the link. whatever memory used by the overlay comes under the address space of computer
B. TRUE Optimal binary search tree construction can be performed efficiently by using dynamic programming.
C. FALSE Depth first search can be used to find connected components of a graph.
D. FALSE Infix + (postfix or prefix) is req. to construct the binary tree uniquely.
|
159 docs|30 tests
|
FAQs on Previous Year Questions: Binary Tree - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is a binary tree in computer science? |  |
| 2. How is a binary tree different from other tree data structures? |  |
| 3. What is the significance of a binary tree in computer science algorithms? |  |
| 4. How can a binary tree be traversed in computer science? |  |
| 5. Can a binary tree have a node with only one child? |  |
















