Q1: For a Boolean variable x, which of the following statements is/are FALSE? (2024 SET-2)
(a) x.1 = x
(b) x + 1 = x
(c) x . x = 0
(d)
Ans: (b, c)
Sol:
- x.1 = x identity law. it is true.
- x + 1 = x it is false. it should be x + 1 = 1
- x . x = 0 it is false, it should be x . x = x
 complement law. it is true
complement law. it is true
So option (B, C) is false here.
Q2: Consider a Boolean expression given by F(X, Y, Z) = Σ(3, 5, 6, 7).
Which of the following statements is/are CORRECT? (2014 SET-1)
(a) F(X, Y, Z) = II(0, 1, 2, 4)
(b) F(X, Y, Z) = XY + YZ + XZ
(c) F(X, Y, Z) is independent of input Y
(d) F(X, Y, Z) is independent of input X
Ans: (a,b)
Sol:

⇒ F(X, Y, Z) = II(0, 1, 2, 4)
⇒ F(X, Y, Z) = XY + XZ + Y
This implies F(X, Y, Z) is dependent on both X and Y.
Answer - A, B
Q3: Consider a Boolean function f (w, x, y, z) such that
f(w, 0, 0, z) = 1
f(1, x, 1, z) = x + z
f(w, 1, y, z) = wz + y
The number of literals in the minimal sum-of-products expression of f is ______ (2021 SET-2)
(a) 4
(b) 6
(c) 8
(d) 9
Ans: (b)
Sol:

We can see 3 squares, so number of literals = 3 x 2 = 6.
Q4: Consider the following Boolean expression.

Which of the following Boolean expressions is/are equivalent to (complement of F)? (2021 SET-1)
(complement of F)? (2021 SET-1)
(a)
(b) 
(c)
(d)
Ans: (b, c, d)
Sol:



Ans: B, C, D
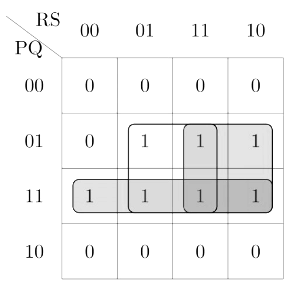
Q5: Consider the Boolean function z(a, b, c).
 Which one of the following minterm lists represents the circuit given above? (2020)
Which one of the following minterm lists represents the circuit given above? (2020)
(a) z = Σ(0, 1, 3, 7)
(b) z = Σ(1, 4, 5, 6, 7)
(c) z = Σ(2, 4, 5, 6, 7)
(d) z = Σ(2, 3, 5)
Ans: (b)
Sol:
From given circuit z = a + b'c
K-Map for the above expression is:

Minterms are ∑(1, 4, 5, 6, 7)
Hence, option (B) is correct
Q6: What is the minimum number of 2-input NOR gates required to implement 4-variable function expressed in sum-of-minterms from as f = 2(0, 2, 5, 7, 8, 10, 13, 15)? Assume that all the inputs and their complements are available. Answer _______. (2019)
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (b)
Sol:

f = (B' + D). (B + D')
It is mentioned that both Complimentary as well as Uncomplimentary forms are available.
B' NOR D = (B' + D)'
B NOR D' = (B + D')'
(B' NOR D) NOR (B NOR D')
= ((B' + D)' + (B + D')')'
= ((B' + D)". (B + D')")
= ((B' + D). (B + D'))
= f
Thus, 3 NOR Gates are required.
Q7: Consider three 4-variable functions f1, f2 and f3, which are expressed in sum-of-minterms
f1 = Σ(0, 2, 5, 8, 14)
f2 = Σ(2, 3, 6, 8, 14, 15)
f3 = Σ(2, 7, 11, 14)
For the following circuit with one AND gate and one XOR gate, the output function f can be expressed as: (2019)
 (a) Σ(7, 8, 11)
(a) Σ(7, 8, 11)
(b) Σ(2, 7, 8, 11, 14)
(c) Σ(2, 14)
(d) Σ(0, 2, 3, 5, 6, 7, 8, 11, 14, 15)
Ans: (a)
Sol:
Perform f1. f2 first, then with the result perform XOR with f3-
f1 . f2 means just take common minterms in f1 and f2 (WHY? due to AND gate present, the minterm should be present in both functions.)
f1 . f2 = Σ(0, 2, 5, 8, 14) . Σ(2, 3, 6, 8, 14, 15) = Σ(2, 8, 14)
Σ(2, 8, 14) ⊕ Σ(2, 7, 11, 14) = Σ(7, 8, 11)
Q8: Which one of the following is NOT a valid identity? (2019)
(a) (x ⊕ y) ⊕ z = x ⊕ (y ⊕ z)
(b) (x + y) ⊕ z = x ⊕ (y + z)
(c) x ⊕ y = x + y, if xy = 0
(d) x ⊕ y = (xy + x'y')'
Ans: (b)
Sol:
1. XOR is associative so (x ⊕ y) ⊕ z = x ⊕ (y ⊕ z)
2. For 2 input, XOR and XNOR are complement to each other i.e. x ⊕ y = (xy + x'y')'
3. x ⊕ y = x + y if xy = 0
Only false statement is option B.
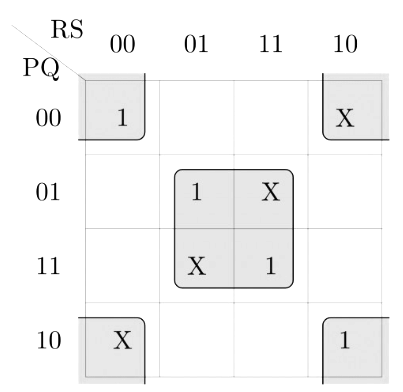
Q9: Consider the minterm list form of a Boolean function F given below.
F(P, Q, R, S) = ∑ m(0, 2, 5, 7, 9, 11) + d(3, 8, 10, 12, 14)
Here, m denotes a minterm and d denotes a don't care term. The number of essential prime implicants of the function F is _____. (2018)
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (b)
Sol:

Implicant: Any product term p in SOP form such that p f is an implicant of f. So, we have 9 implicants for F here one corresponding to each 1 or d in the K-map.
Prime Implicant: A minimal implicant is called a prime implicant (no extra literals than required). So, we have 5 prime implicants for . (for each 1 or d in K - map try to combine with near by 1s and do not care conditions)
. (for each 1 or d in K - map try to combine with near by 1s and do not care conditions)
Essential Prime Implicant: A prime implicant which cannot be replaced by any other for getting the output. i.e.,
essential prime implicants cover the output that no other combination of other prime implicants can. In K-map, this means an essential prime implicant must cover a 1
(we do not consider don't care as essential) which is not covered by any other prime implicant.
Here, we have 3 essential prime implicants corresponding to 3 selections shown in the below K - mар.
Q10: Let ⊕ and denote the Exclusive OR and Exclusive NOR operations, respectively. Which one of the following is NOT CORRECT? (2018)
denote the Exclusive OR and Exclusive NOR operations, respectively. Which one of the following is NOT CORRECT? (2018)
(a)
(b)
(c)
(d)
Ans: (d)
Sol:
Consider Option(D). LHS can be simplified as,

Similarly, for RHS

LHS ≠ RHS therefore, Option (D) is the correct answer.
Other options can be simplified as follows.

Q11: Given f(w, x, y, z) = ∑m (0, 1, 2, 3, 7, 8, 10) + Σd (5, 6, 11, 15), where d represents the don't care condition in Karnaugh maps. Which of the following is a minimum product-of-sums (POS) form of f(w, x, y, z)? (2017 SET-2)
(a)
(b)
(c)
(d)
Ans: (a)
Sol:


Q12: If w, x, y, z are Boolean variables, then which one of the following is INCORRECT ? (2017 SET-2)
(a) wx + w(x + y) + x(x + y) = x + wy
(b)
(c)
(d) (w + y)(wxy + wyz) = wxy + wyz
Ans: (c)
Sol:
Let us try to simplify (minimize) the expression given in each option
Option - A: wx + w(x + y) + x(x + y) = x + wy
wx + wx + wy + x
wx + wy + x
x(1 + w) + wy
x + wy
Option - B: 

Option - D: (w + y) (wxy + wyz) = wxy + wyz
wxy + wyz + wxy + wyz
wxy + wyz
Option A, B, D are matching fine.
Hence, Option - C is the answer
Q13: Consider the Karnaugh map given below, where x represents "don't care" and blank represents 0.
 Assume for all inputs (a, b, c, d) the respective complements
Assume for all inputs (a, b, c, d) the respective complements are also available. The above logic is implemented 2-input NOR gates only. The minimum number of gates required is _______. (2017 SET-1)
are also available. The above logic is implemented 2-input NOR gates only. The minimum number of gates required is _______. (2017 SET-1)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (a)
Sol:
From K-map simplification we get the min-term as CA'. So We can simplyfy it for NOR gate expression
I.e. C' NOR A = (C' + A)' = CA'
Now complemented inputs are also given to us so, for 2 input NOR gate we need only 1 NOR gate.
1 is correct answer.
Q14: Let, x1 ⊕ x2 ⊕ x3 ⊕ x4 = 0 where x1, x2, x3, x4 are Boolean variables, and is the XOR operator.
Which one of the following must always be TRUE? (2016 SET-2)
(a) x1, x2, x3, x4 = 0
(b) x1 x3 + x2 = 0
(c)
(d) x1 + x2 + x3 + x4 = 0
Ans: (c)
Sol:
Let x1 = 1 x2 = 1 x3 = 1 and x4 = 1
such that x1 ⊕ x2 ⊕ x3 ⊕ x4 = 1 ⊕ 1 ⊕ 1 ⊕ 1 = 0
A. x1, x2, x3, x4 = 1.1.1.11, False
B. x1 x3 + x2 = 1.1 + 1 = 1, False
C. is always True.
D. x1 + x2 + x3 + x4 = 1 + 1 + 1 + 1 = 1, False
Correct Answer: C
Q15: Consider the Boolean operator with the following properties: (2016 SET-1)
x#0 = x, x#1 =  , x#x = 0 and
, x#x = 0 and  #2 = 1. Then x#y is equivalent to
#2 = 1. Then x#y is equivalent to
(a)
(b)
(c)
(d)
Ans: (a)
Sol:
These are properties of XOR function.. so answer is A)
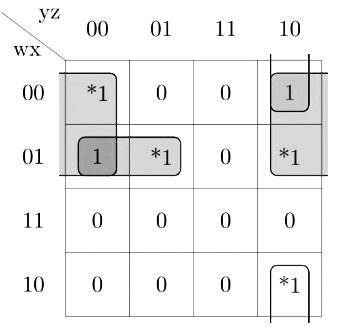
Q16: The total number of prime implicants of the function f(w, x, y, z) = Σ(0, 2, 4, 5, 6, 10) is ______. (2015 SET-3)
(a) 2
(b) 3
(c) 5
(d) 6
Ans: (b)
Sol:

As you can see that there is one 4-set and two 2-set that are covering the star marked 1's
(i.e. the ones that are not covered by any other combinations)
So, the answer is 3.
Q17: Given the function F = P' + QR, where F is a function in three Boolean variables P,Q and R and P' = !P,
consider the following statements. (2015 SET-3)
(S1) F = Σ(4, 5, 6)
(S2) F = Σ(0, 1, 2, 3,7)
(S3) F = II(4, 5, 6)
(S4) F = II(0, 1, 2, 3, 7)
Which of the following is true?
(a) (S1)- False, (S2)- True, (S3)- True, (S4)- False
(b) (S1)- True, (S2)- False, (S3)- False, (S4)- True
(c) (S1)- False, (S2)- False, (S3)- True, (S4)- True
(d) (S1)- True, (S2)- True, (S3)- False, (S4)- False
Ans: (a)
Sol:
F = P' + QR, draw the Kmap for this
We can find the minterm ∑(0, 1, 2, 3, 7) and maxterm II(4, 5, 6)
So, option A is correct: (S1)-False, (S2)-True, (S3)-True, (S4)-False
Q18: Let # be a binary operator defined as X#Y = X'+Y' where X and Y are Boolean variables.
Consider the following two statements. (2015 SET-3)
(S1) (P # Q) # R = P # (Q # R)
(S2) Q # R = R # Q
Which of the following is/are true for the Boolean variables P, Q and R?
(a) Only S1 is true
(b) Only S2 is true
(c) Both S1 and S2 are true
(d) Neither S1 nor S2 are true
Ans: (b)
Sol:
Answer: B
(P # Q)#R = (P' + Q')#R
= P. Q + R'
whereas,
P#(Q # R) = P' + (Q # R)'
= P' + (Q' + R')'
= P' + QR
Q19: The number of min-terms after minimizing the following Boolean Algebra is _________. (2015 SET-2)
[D' + AB' + AC' + AC'D + A'C'D]'
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (b)
Sol:
F = [D' + AB' + A'C + AC'D + A'C'D]'
F' = D' + AB' + A'C + AC'D + A'C'D
Now we have F', so fill 0's (maxterms) in K-map for each term
As for D'

Similarly for AB', A'C, AC'D and A'C'D. We will get

We get one place for min-term and that is ABCD
Q20: Consider the operations
f(X, Y, Z) = X'Y Z + XY' + Y'Z' and g(X, Y, Z) = X'Y Z + X'YZ' + XY.
Which one of the following is correct? (2015 SET-1)
(a) Both {f} and {g} are functionally complete
(b) Only {f} is functionally complete
(c) Only {g} is functionally complete
(d) Neither {f} nor {g} is functionally complete
Ans: (b)
Sol:
g is preserving 0 as when all inputs are zero, output is always 0 and so g cannot be functionally complete.
f is not preserving 0.
f is not preserving 1. (when all inputs are 1, output is 0).
f is not linear as in XY' only one (odd) input (X = 1, Y =Z= 0) needs to be 1 and in X'YZ two inputs (even) (X = 0, Y = Z = 1) need to be 1.
f is not monotone as changing Y from 0 to 1, can take f from 1 to 0.
f is not self dual as f(X, Y, Z) ≠ -f(-X, -Y, -Z)
So, f satisfies all 5 conditions required for functional completeness.
Hence, B is the answer.
Q21: Let denote the Exclusive OR (XOR) operation. Let '1' and '0' denote the binary constants. Consider the following Boolean Algebra for F over two variables P and Q. (2014 SET-3)
F(P, Q) = ((1 ⊕ P) ⊕ (P ⊕ Q)) ⊕ ((P ⊕ Q) ⊕ (Q ⊕ 0))
The equivalent expression for F is
(a) P + Q
(b)
(c) P ⊕ Q
(d)
Ans: (d)
Sol:
XOR is associative and commutative. Also, A ⊕ A = 0 and A ⊕ 1 = and A ⊕ 0 = A.
and A ⊕ 0 = A.
So
((1⊕ P) ⊕ (P ⊕ Q)) ⊕ ((P ⊕ Q) ⊕ (Q ⊕ 0))
⇒ (1 ⊕ P) ⊕ ((P ⊕ Q) ⊕ (P ⊕ Q)) ⊕ (Q ⊕ 0)
⇒ (1 ⊕ 0) ⊕ (P ⊕ Q)
⇒ 1 ⊕ (P ⊕ Q)
⇒
Correct Answer: D
Q22: Consider the following minterm expression for F. (2014 SET-3)
F(P,Q,R,S) = ∑ 0, 2, 5, 7, 8, 10, 13, 15
The minterms 2, 7, 8 and 13 are 'do not care terms. The minimal sum of-products form for F is
(a)
(b)
(c)
(d)
Ans: (b)
Sol:
While putting the terms to K-map the 3rd and 4th columns are swapped so, do 3rd and 4th rows. So, term 2 is going to (0, 3) column instead of (0, 2), 8 is going to (3,0) instead of (2,0) etc.

Solving this k-map gives B) as the answer.
Q23: The dual of a Boolean function F(x1, x2,..., xn, +, ⋅ ,'), written as FD, is the same expression as that of F with + and ⋅ swapped. F is said to be self-dual if F = FD. The number of self-dual functions with n Boolean variables is (2014 SET-2)
(a) 2n
(b) 2n-1
(c)
(d)
Ans: (d)
Sol:
A function is self dual if it is equal to its dual (A dual function is obtained by interchanging. and +).
For self-dual functions,
1. Number of min terms equals number of max terms
2. Function should not contain two complementary minterms whose sum equals 2-1,
where n is the number of variables.

So, here (0, 7) (1, 6) (2, 5) (3, 4) are complementary terms so in self-dual we can select any one of them but not both.
Totally 2 x 2 x 2 x 2 = 24 possibility because say from (0, 7) we can pick anyone in minterm but not both.
For example, let f = ∑(0, 6, 2, 3)
NOTE: here I have taken only one of the complementary term for min term from the sets
So, remaining numbers will go to MAXTERMS
For above example, 24 = 16 self dual functions are possible
So, if we have N variables, total Minterms possible is 2n
Then half of them we selected so 2n-1.
Now we have 2 choices for every pair for being selected.
So total such choices 
 (option D)
(option D)
Q24: Consider the following Boolean Algebra for F: (2014 SET-1)

The minimal sum-of products form of F is
(a) PQ + QR + QS
(b) P + Q + R + S
(c)
(d)
Ans: (a)
Sol:

Minimal SOP = PQ + QR + QS
Hence, option A is correct.
Q25: Which one of the following expressions does NOT represent exclusive NOR of x and y? (2013)
(a) xy + x' y'
(b) x ⊕ y'
(c) x' ⊕ y
(d) x' ⊕ y'
Ans: (d)
Sol:
A: means both are either true OR both are false. then it will be true = EXNOR
B & C: whenever any one of the literal is complemented then ExOR can be turned to ExNOR and complement sign on the literal can be removed. So these two also represents EXNOR operation of x and y.
Answer is option D. It is the ExOR operation b/w the two.
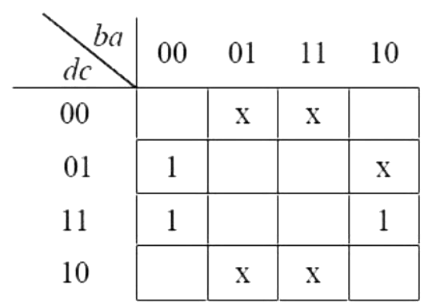
Q26: What is the minimal form of the Karnaugh map shown below? Assume that X denotes a don't care term. (2012)
 (a)
(a)
(b)
(c)
(d)
Ans: (b)
Sol:

2 quads are getting formed.
Value for First one is b' d' and value for 2nd one is b' c'. So, answer is option B.
Q27: The truth table

represents the Boolean function (2012)
(a) x
(b) x + y
(c) x ⊕ y
(d) y
Ans: (a)
Sol:
Whenever X is true (X, Y) is true and whenever X is false (X, Y) is false,
so the answer is (A) X.
Q28: The simplified SOP (Sum of Product) form of the Boolean Algebra (2011)

(a)
(b)
(c)
(d) (PQ + R)
Ans: (b)
Sol:

Answer is B
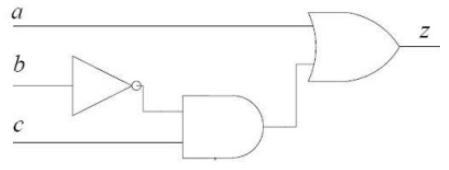
Q29: Which one of the following circuits is NOT equivalent to a 2-input XNOR (exclusive NOR) gate? (2011)

(a) A
(b) B
(c) C
(d) D
Ans: (d)
Sol:
A. (AB' + A'B)' = A B
B
B. (A'(Β')' + (A')'B')' = (A ⊕ B)' = A B
B
C. A'B' + (A')'B = A B
B
D. ((AB')'. (A + B'))' = (AB') + (A + B')' = AB' + A'B = A ⊕ B
So, Answer is (D)
Q30: What is the Boolean Algebra for the output f of the combinational logic circuit of NOR gates given below? (2010) (a)
(a)
(b)
(c)
(d)
Ans: (a)
Sol:
Level 1:

Level 2:

Level 3:

∴ Answer : Option A
Q31: The minterm expansion of is (2010)
is (2010)
(a) m2 + m4 + m6 + m7
(b) m0 + m1 + m3 + m5
(c) m0 + m1 + m6 + m7
(d) m2 + m3 + m4 + m5
Ans: (a)
Sol:


Minterm expansion of f(P, Q, R) is m2 + m4 + m6 + m7

 complement law. it is true
complement law. it is true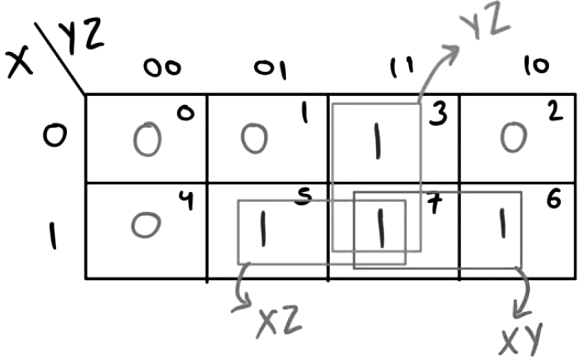


 (complement of F)? (2021 SET-1)
(complement of F)? (2021 SET-1)



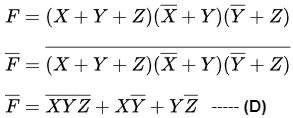

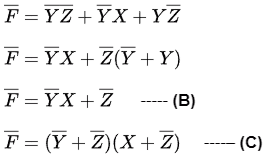
 Which one of the following minterm lists represents the circuit given above? (2020)
Which one of the following minterm lists represents the circuit given above? (2020)

 (a) Σ(7, 8, 11)
(a) Σ(7, 8, 11)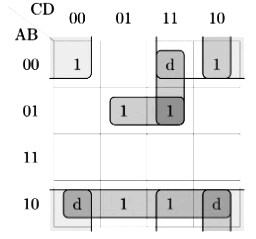
 . (for each 1 or d in K - map try to combine with near by 1s and do not care conditions)
. (for each 1 or d in K - map try to combine with near by 1s and do not care conditions) denote the Exclusive OR and Exclusive NOR operations, respectively. Which one of the following is NOT CORRECT? (2018)
denote the Exclusive OR and Exclusive NOR operations, respectively. Which one of the following is NOT CORRECT? (2018)





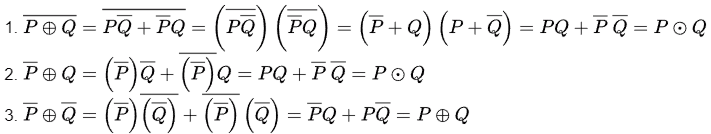










 Assume for all inputs (a, b, c, d) the respective complements
Assume for all inputs (a, b, c, d) the respective complements are also available. The above logic is implemented 2-input NOR gates only. The minimum number of gates required is _______. (2017 SET-1)
are also available. The above logic is implemented 2-input NOR gates only. The minimum number of gates required is _______. (2017 SET-1)
 , x#x = 0 and
, x#x = 0 and  #2 = 1. Then x#y is equivalent to
#2 = 1. Then x#y is equivalent to








 and A ⊕ 0 = A.
and A ⊕ 0 = A.







 (option D)
(option D) 


 (a)
(a)










 B
B B
B B
B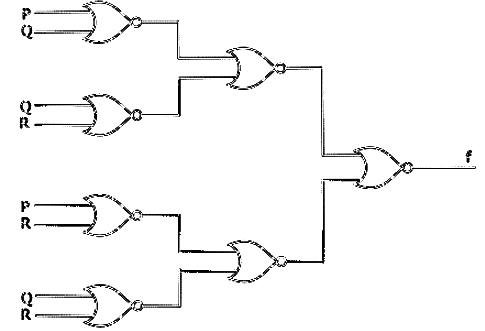 (a)
(a)




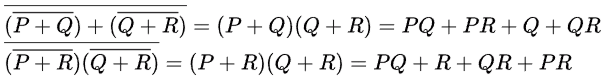

 is (2010)
is (2010)








 complement law. it is true
complement law. it is true
















