Previous Year Questions: Cache Memory | Computer Architecture & Organisation (CAO) - Computer Science Engineering (CSE) PDF Download
Q1: A given program has 25% load/store instructions. Suppose the ideal CPI (cycles per instruction) without any memory stalls is 2. The program exhibits 2% miss rate on instruction cache and 8% miss rate on data cache. The miss penalty is 100 cycles. The speedup (rounded off to two decimal places) achieved with a perfect cache (i.e., with NO data or instruction cache misses) is _________ (2024 SET-1)
(a) 2.25
(b) 1.45
(c) 3
(d) 3.85
Ans: (c)
Sol: CPI with a Perfect Cache: 2
CPI with the Actual Cache: 2 (ideally) + 0.02 × 100 (stall cycles for instruction cache miss) + 0.25 × 0.08 × 100 (stall cycles for data cache miss) = 6
Speedup with a perfect cache = 6/2 = 3.
Q2: Consider two set-associative cache memory architectures: WBC, which uses the write back policy, and WTC, which uses the write through policy. Both of them use the LRU (Least Recently Used) block replacement policy. The cache memory is connected to the main memory. Which of the following statements is/are TRUE? (2024 SET-1)
(a) A read miss in WBC never evicts a dirty block
(b) A read miss in WTC never triggers a write back operation of a cache block to main memory
(c) A write hit in WBC can modify the value of the dirty bit of a cache block
(d) A write miss in WTC always writes the victim cache block to main memory before loading the missed block to the cache
Ans: (b, c)
Sol: A. False
When we miss accessing data in the cache (either by reading or writing), we can choose whether or not to add that missed data into the cache. Sometimes, we might decide not to add it because the data already in the cache from another memory location is more useful or accessed more often.
So, the statement is false because it says that a read miss in WBC "never" removes a dirty block, which is not always the case.
B. True
In the write-through policy, data is always kept synchronized. Therefore, we never need to perform a "write back" operation to remove any entry from the cache. This makes the option correct because it states that "never" triggers a write-back.
C. True
A write hit in WBC can modify the value of the dirty bit of a cache block.
If there's a write hit in WBC, it means we're writing directly into the cache. So, of course, we'll also change the dirty bit.
D. False
A write miss in WTC always writes the victim cache block to main memory before loading the missed block to the cache.
There are two blocks mentioned: a missed block and a victim block. The missed block is the one we want to access, while the victim block is the one replaced by LRU.
When there's a write miss in WTC, it means the data we're trying to write isn't in the cache. Now, we may want to load it into the cache, or we may not want to. Suppose we don't want to bring it into the cache; in that case, we can directly modify the main memory.
However, if we decide to bring it into the cache, then we may or may not need to replace the victim block depending on cache is already full or not
Q3: An 8-way set associative cache of size 64 KB (1 KB = 1024 bytes) is used in a system with 32-bit address. The address is sub-divided into TAG, INDEX, and BLOCK OFFSET.
The number of bits in the TAG is ____. (2023)
(a) 18
(b) 19
(c) 20
(d) 21
Ans: (b)
Sol: 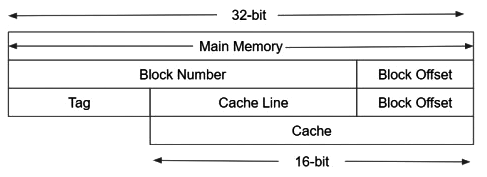 System is 32-bit address.
System is 32-bit address.
Cache Size : 64 KB = 26 ∗ 210 = 216. So, cache bits = 16.
So Tag Bits = 32 – 16 = 16 bit.
NOTE : If cache is k-way set associative then we have to transfer log2k bits from cache line bits to Tag bits.
As, Cache is 8-way set associative. So, we have to transfer 3 bits to tag side.
So, final Tag bits = 16 + 3 = 19.
Number of bits in Tag Field = 19.
Q4: Consider a system with 2 KB direct mapped data cache with a block size of 64 bytes. The system has a physical address space of 64 KB and a word length of 16 bits. During the execution of a program, four data words P, Q, R, and S are accessed in that order 10 times (i.e., PQRSPQRS...). Hence, there are 40 accesses to data cache altogether. Assume that the data cache is initially empty and no other data words are accessed by the program. The addresses of the first bytes of P, Q, R, and S are 0xA248, 0xC28A, 0xCA8A, and 0xA262, respectively. For the execution of the above program, which of the following statements is/are TRUE with respect to the data cache?
MSQ (2022)
(a) Every access to S is a hit.
(b) Once P is brought to the cache it is never evicted.
(c) At the end of the execution only R and S reside in the cache.
(d) Every access to R evicts Q from the cache.
Ans: (a, b, d)
Sol: Physical memory = 64KB ===> 16 bits required to represent Physical memory
Cache memory = 2KB ===> 11 bits for cache memory
Block size = 64 B = 32 words ===> 6 bits because of system is Byte addressable.
Tag = 16-11 = 5 bits
Cache index = 11-6 = 5 bits
Block offset = 6 bits
P = 0XA248 = 1010 0010 0100 1000 = 1010001001001000 ( Tag – cache index – Block offset )
Q = 0XC28A = 1100 0010 1000 1010 = 1100001010001010
R = 0XCA8A = 1100 1010 1000 1010 = 1100101010001010
S = 0XA262 = 1010 0010 0110 0010 = 1010001001100010
Given that, Direct mapped cache,
If we observe, P and S are belongs to same Block ( Tag and cache bits are same ). Therefore every access of S should result in a hit due to neither Q nor R competing for the same cache block and once P brought to the cache, it is never evicted.
If we observe Q and R, those are competing for same cache block. So at the end R only present in the cache due to R is accessed at last. ( compaing to Q ) and every access to R evicts Q from the Cache.
Therefore at the end, P, R and S in the Cache.
Options A, B and D are true.
Q5: A cache memory that has a hit rate of 0.8 has an access latency 10 ns and miss penalty 100 ns. An optimization is done on the cache to reduce the miss rate. However, the optimization results in an increase of cache access latency to 15 ns, whereas the miss penalty is not affected. The minimum hit rate (rounded off to two decimal places) needed after the optimization such that it should not increase the average memory access time is _____. (2022)
(a) 0.92
(b) 0.88
(c) 0.76
(d) 0.85
Ans: (d)
Sol: For a given cache, Average memory access time can be computed as:
AMAT= HitTime + Miss rate ∗ Miss Penalty
Initially,
Hit rate of cache = 0.8
∴Miss rate = 0.2
Access Latency = HitTime = 10ns
Miss Penalty = 100ns
∴ AMATunoptimized = 10 + 0.2(100) = 30ns
For the optimized cache,
Access Latency = HitTime = 15ns
∴ AMAToptimized = 15 + x(100)
Now,
AMATunoptimized ≥ AMAToptimized
30 ≥ 15 + 100x
⇒15 ≥ 100x
⇒ 0.15 ≥ x
⇒ 0.85 ≤ 1−x
∴The required hit rate = (1 − x) = 0.85
Q6: Let WB and WT be two set associative cache organizations that use LRU algorithm for cache block replacement. WB is a write back cache and WT is a write through cache. Which of the following statements is/are FALSE?
MSQ (2022)
(a) Each cache block in WB and WT has a dirty bit.
(b) Every write hit in WB leads to a data transfer from cache to main memory.
(c) Eviction of a block from WT will not lead to data transfer from cache to main memory.
(d) A read miss in WB will never lead to eviction of a dirty block from WB.
Ans: (a, b, d)
Sol: WB Cache: Updates to the cache block don’t result in Updates to the Main Memory immediately. Burst Writes are preferred for higher throughput and those needing higher write performance.
WT Cache: Updates to the Cache block are reflected on Main Memory before carrying out other processes. Consistency is preferred.
(a) A WB must necessarily have a dirty bit to avoid redundant writes to Main Memory. Whereas a WT cache needn’t as the change is reflected after a write. False
(b) A WB cache’s primary use is to increase throughput or useful work. Multiple writes to the same cache block will not be reflected immediately, avoiding unnecessary data transfer time. False
(c) WT cache’s main goal is to prefer consistency overwrite performance, and a cache block is made to reflect the current main memory. True
(d) LRU doesn’t have specific replacement strategies for dirty and regular blocks. Hence a read miss might evict a dirty block. False
Q7: Assume a two-level inclusive cache hierarchy, L1 and L2, where L2 is the larger of the two. Consider the following statements.
S1: Read misses in a write through L1 cache do not result in writebacks of dirty lines to the L2
S2: Write allocate policy must be used in conjunction with write through caches and no-write allocate policy is used with writeback caches.
Which of the following statements is correct? (2021 SET-2)
(a) S1 is true and S2 is false
(b) S1 is false and S2 is true
(c) S1 is true and S2 is true
(d) S1 is false and S2 is false
Ans: (a)
Sol: S1: Read Miss in a write through L1 cache results in read allocate. No write back is done here, as in a write through L1 cache, both L1 and L2 caches are updated during a write operation (no dirty blocks and hence no dirty bits as in a write back cache). So during a Read miss it will simply bring in the missed block from L2 to L1 which may replace one block in L1 (this replaced block in L1 is already updated in L2 and so needs no write back). So, S1 is TRUE.
S2: This statement is FALSE. Both write-through and write-back policies can use either of these write-miss policies, but usually they are paired in this way.
- No write allocation during write through as L1 and L2 are accessed for each write operation (subsequent writes to same location gives no advantage even if the location is in L1 cache).
- In write back we can to do write allocate in L1 after a write operation hoping for subsequent writes to the same location which will then hit in L1 and thus avoiding a more expensive L2 access.
Correct Answer: A.
Q8: Consider a set-associative cache of size 2KB (1KB = 210 bytes) with cache block size of 64 bytes. Assume that the cache is byte-addressable and a 32 -bit address is used for accessing the cache. If the width of the tag field is 22 bits, the associativity of the cache is ______ (2021 SET-2)
(a) 2
(b) 4
(c) 8
(d) 16
Ans: (a)
Sol: 32bit address is used for accessing the cache.
It is given that cache is Set-Associative.
The address bits get split as follows: Block Size = 64B ⇒ Block offset = 6 bits.
Block Size = 64B ⇒ Block offset = 6 bits.
Given that Tag field width =22 bits.
Therefore, width of Set Index field = 32 − 22 − 6 = 4 ⇒ 24 = 16 sets in the cache.
Cache size is 2KB and Block size = 64B ⇒ 25 = 32 blocks present in the cache.
16 sets contain 32 blocks ⇒2 blocks per set or associativity = 2.
Correct Answer: 2
Q9: Consider a computer system with a byte-addressable primary memory of size 232 bytes. Assume the computer system has a direct-mapped cache of size 32KB(1KB = 210 bytes), and each cache block is of size 64 bytes.
The size of the tag field is __________ bits. (2021 SET-1)
(a) 22
(b) 15
(c) 17
(d) 19
Ans: (c)
Sol: Tag bits = PASbits–log2(Cache Size) + log2(K) (where K is associativity)
= 32 - 15 + 0 = 17 bits
Q10: How many total bits are required for a direct-mapped cache with 128 KB of data and 1 word block size, assuming a 32-bit address and 1 word size of 4 bytes? (2020)
(a) 2 Mbits
(b) 1.7 Mbits
(c) 2.5 Mbits
(d) 1.5 Mbits
Ans: (d)
Sol: Data cache =128KB
Block Size = 1W = 4Bytes = 32bits
Main Memory address = 32 ∴ Number of cache lines
∴ Number of cache lines Now,
Now,
Tag Memory Size = Number of lines in cache memory×Tag space in the line = 215 × 15bit
Total Cache Size = Tag Memory size + Data Memory size = 215 × (15 + 32) = 1.5Mb
Q11: Which of the following is an efficient method of cache updating? (2020)
(a) Snoopy writes
(b) Write through
(c) Write within
(d) Buffered write
Ans: (a)
Sol: Write through protocol updates (or invalidates) the shared data, as and when needed. It asks to update/invalidate via broadcasting (hence, not efficient, as it creates traffic)
Buffered write is an added functionality to write through cache. (Hence, not efficient, again)
Write back protocol is based on ownership of a block. (Read page 454 of Hamacher, 6th Ed). It also uses broadcast and creates traffic, hence, not efficient.
Though, the traffic generated is less than Write through.
"the abilities of cache controllers to observe the activity on the bus and take appropriate actions are called snoopy-cache techniques.
For performance reasons, it is important that the snooping function not interfere with the normal operation of a processor and its cache."
Hence, efficient.
Q12: A computer system with a word length of 32 bits has a 16 MB byte- addressable main memory and a 64 KB, 4-way set associative cache memory with a block size of 256 bytes. Consider the following four physical addresses represented in hexadecimal notation.
A1 = 0 x 42C8A4,
A2 = 0 x 546888,
A3 = 0 x 6A289C,
A4 = 0 x 5E4880
Which one of the following is TRUE? (2020)
(a) A1 and A4 are mapped to different cache sets.
(b) A2 and A3 are mapped to the same cache set.
(c) A3 and A4 are mapped to the same cache set.
(d) A1 and A3 are mapped to the same cache set.
Ans: (b)
Sol: Block size is 256 Bytes. Number of sets in cache = 26 so Set offset bits = 6 and word offset bits = 8.
So check for set, check for the rightmost 4 digits of each physical address.(Last two byte denote the word address)
A1=C8A4 = C8 = 11001000
A2=6888 = 68 = 01101000
A3=289C = 28 = 00101000
A4=4880 = 48 = 01001000
Now look for lowest order 6 bits in the highlighted part of Each physical address(corresponds to set number).
8 and 8 match and 6=0110 and 2=0010 two low order bits of 6 and 2 match, So A2 and A3 go to same set.
So answer-B.
Q13: A direct mapped cache memory of 1 MB has a block size of 256 bytes. The cache has an access time of 3 ns and a hit rate of 94%. During a cache miss, it takes 20 ns to bring the first word of a block from the main memory, while each subsequent word takes 5 ns. The word size is 64 bits. The average memory access time in ns (round off to 1 decimal place) is______. (2020)
(a) 8.2
(b) 6.25
(c) 13.5
(d) 15.2
Ans: (c)
Sol: Block size is 256 Bytes,word size is 64 bits or 8 bytes. So Block size in words is 8 words.
Number of words per block = 32
Time to fetch a word from main-memory to cache is: 20 + 31 × 5 = 175ns because first word takes 20ns and rest each subsequent words take 5ns each.
So average Memory acces time is 0.94(3) + 0.06(3 + 175) = 13.5 ns
Q14: A certain processor deploys a single-level cache. The cache block size is 8 words and the word size is 4 bytes. The memory system uses a 60-MHz clock. To service a cache-miss, the memory controller first takes 1 cycle to accept the starting address of the block, it then takes 3 cycles to fetch all the eight words of the block, and finally transmits the words of the requested block at the rate of 1 word per cycle. The maximum bandwidth for the memory system when the program running on the processor issues a series of read operations is _________× 106 bytes/sec. (2019)
(a) 80
(b) 160
(c) 320
(d) 128
Ans: (b)
Sol: Time to transfer a cache block = 1+3+8 = 12 cycles.
i.e., 4 bytes × 8 = 32 bytes in 12 cycles.
So, memory bandwidth =  = 160 x 106 bytes/s
= 160 x 106 bytes/s
Q15: A certain processor uses a fully associative cache of size 16 kB, The cache block size is 16 bytes. Assume that the main memory is byte addressable and uses a 32-bit address. How many bits are required for the Tag and the Index fields respectively in the addresses generated by the processor? (2019)
(a) 24 bits and 0 bits
(b) 28 bits and 4 bits
(c) 24 bits and 4 bits
(d) 28 bits and 0 bits
Ans: (d)
Sol: Given that cache is Fully Associative. There are no index bits in fully associative cache because every main memory block can go to any location in the cache ⇒ Index bits = 0.
There are no index bits in fully associative cache because every main memory block can go to any location in the cache ⇒ Index bits = 0.
Given that memory is byte addressable and uses 32-bit address.
Cache Block size is 16 Bytes ⇒ Number of bits required for Block Offset = ⌈log216⌉ = 4 bits
∴ Number of Tag bits = 32−4 = 28.
Answer is (D).
Q16: For a multi-processor architecture, in which protocol a write transaction is forwarded to only those processors that are known to possess a copy of newly altered cache line? (2018)
(a) Snoopy bus protocol
(b) Cache coherency protocol
(c) Directory based protocol
(d) None of the above
Ans: (c)
Q17: The size of the physical address space of a processor is 2P bytes. The word length is 2W bytes. The capacity of cache memory is 2N Bytes. The size of each cache block is 2M words. For a K-way set-associative cache memory, the length (in number of bits) of the tag field is (2018)
(a) P−N−log2K
(b) P−N+log2K
(c) P−N−M−W−log2K
(d) P−N−M−W+log2K
Ans: (b)
Sol: Physical Address Space = 2P Bytes i.e. P bits to represent size of total memory.
Cache Size = 2N Byte i.e., N bits to represent Cache memory.
Tag size = 2X Bytes i.e., X bits to represent Tag.
Cache is K− way associative.
 ⇒ X (Size of Tag in bits) = P - N + log(K)
⇒ X (Size of Tag in bits) = P - N + log(K)
Correct Answer: B
Q18: A cache memory needs an access time of 30 ns and main memory 150 ns, what is average access time of CPU (assume hit ratio = 80%)? (2017)
(a) 60 ns
(b) 30 ns
(c) 150 ns
(d) 70 ns
Ans: (a)
Sol: Effective Memory Access Time = Cache hit * Cache access time + Cache miss ( Cache miss Penalty + memory Access time)
= 0.8(30) + (1-0.8)(30+150) ns
= 24 + 0.2(180) ns
= 24 + 36 ns = 60 ns.
Option A.
Q19: Consider a machine with a byte addressable main memory of 232 bytes divided into blocks of size 32 bytes. Assume that a direct mapped cache having 512 cache lines is used with this machine. The size of the tag field in bits is ______. (2017 SET-2)
(a) 18
(b) 23
(c) 27
(d) 20
Ans: (a)
Sol: No. of blocks of main Memory = 232/25 = 227
And there are 512 = 29 lines in Cache Memory.
Tag bits tell us to how many blocks does 1 line in Cache memory points to 1 cache line points to 227/29 = 218 lines
So, 18 bits are required as TAG bits.
Q20: The read access times and the hit ratios for different caches in a memory hierarchy are as given below. The read access time of main memory is 90 nanoseconds. Assume that the caches use the referred word-first read policy and the write back policy. Assume that all the caches are direct mapped caches. Assume that the dirty bit is always 0 for all the blocks in the caches. In execution of a program, 60% of memory reads are for instruction fetch and 40% are for memory operand fetch. The average read access time in nanoseconds (up to 2 decimal places) is______. (2017 SET-2)
The read access time of main memory is 90 nanoseconds. Assume that the caches use the referred word-first read policy and the write back policy. Assume that all the caches are direct mapped caches. Assume that the dirty bit is always 0 for all the blocks in the caches. In execution of a program, 60% of memory reads are for instruction fetch and 40% are for memory operand fetch. The average read access time in nanoseconds (up to 2 decimal places) is______. (2017 SET-2)
(a) 5.4
(b) 3.7
(c) 4.72
(d) 6.1
Ans: (c)
Sol: L2 cache is shared between Instruction and Data (is it always? see below)
So, average read time = Fraction of Instruction Fetch ∗ Average Instruction fetch time + Fraction of Data Fetch ∗ Average Data Fetch Time
Average Instruction fetch Time = L1 access time + L1 miss rate ∗ L2 access time + L1 miss rate ∗ L2 miss rate ∗ Memory access time
= 2 + 0.2 × 8 + 0.2 × 0.1 × 90
= 5.4 ns
Average Data fetch Time = L1 access time + L1 miss rate ∗ L2 access time + L1 miss rate ∗ L2 miss rate ∗ Memory access time = 2 + 0.1 × 8 + 0.1 × 0.1 × 90 = 3.7ns
So, average memory access time = 0.6 × 5.4 + 0.4 × 3.7 = 4.72ns
Now, why L2 must be shared? Because we can otherwise use it for either Instruction or Data and it is not logical to use it for only 1. Ideally this should have been mentioned in question, but this can be safely assumed also (not enough merit for Marks to All). Some more points in the question:
Assume that the caches use the referred-word-first read policy and the writeback policy
Writeback policy is irrelevant for solving the given question as we do not care for writes. Referred-word-first read policy means there is no extra time required to get the requested word from the fetched cache line.
Assume that all the caches are direct mapped caches.
Not really relevant as average access times are given
Assume that the dirty bit is always 0 for all the blocks in the caches
Dirty bits are for cache replacement- which is not asked in the given question. But this can mean that there is no more delay when there is a read miss in the cache leading to a possible cache line replacement. (In a write-back cache when a cache line is replaced, if it is dirty then it must be written back to main memory).
Q21: In a two-level cache system, the access times of L1 and L2 caches are 1 and 8 clock cycles, respectively. The miss penalty from L2 cache to main memory is 18 clock cycles . The miss rate of L1 cache is twice that of L2. The average memory access time (AMAT) of this cache system is 2 cycles. This miss rates of L1 and L2 respectively are : (2017 SET-2)
(a) 0.111 and 0.056
(b) 0.056 and 0.111
(c) 0.0892 and 0.1784
(d) 0.1784 and 0.0892
Ans: (a)
Sol: In two-level memory system (hierarchical), it is clear that the second level is accessed only when first level access is a miss. So, we must include the first level access time in all the memory access calculations. Continuing this way for any level, we must include that level access time (without worrying about the hit rate in that level), to all memory accesses coming to that level (i.e., by just considering the miss rate in the previous level). So, for the given question, we can get the following equation:
AMAT = L1 access time
+L1 miss rate × L2 access time
+L1 miss rate × L2 miss rate × Main memory access time
2 = 1+ x × 8 + 0.5 x2 × 18
⇒ 9x2 + 8x − 1 = 0 So, Answer is option (A).
So, Answer is option (A).
Q22: A cache memory unit with capacity of N words and block size of B words is to be designed. If it is designed as a direct mapped cache, the length of the TAG field is 10 bits. If the cache unit is now designed as a 16-way set-associative cache, the length of the TAG field is ______bits. (2017 SET-1)
(a) 12
(b) 13
(c) 14
(d) 15
Ans: (c)
Sol:  In set-associative 1 set = 16 lines. So the number of index bits will be 4 less than the direct mapped case.
In set-associative 1 set = 16 lines. So the number of index bits will be 4 less than the direct mapped case.
So, Tag bits increased to 14 bits.
Q23: Consider a 2-way set associative cache with 256 blocks and uses LRU replacement, Initially the cache is empty. Conflict misses are those misses which occur due the contention of multiple blocks for the same cache set. Compulsory misses occur due to first time access to the block. The following sequence of accesses to memory blocks.
(0, 128, 256, 128, 0, 128, 256, 128, 1, 129, 257, 129, 1, 129, 257, 129)
is repeated 10 times. The number of conflict misses experienced by the cache is ___________. (2017 SET-1)
(a) 80
(b) 76
(c) 40
(d) 90
Ans: (b)
Sol: {0, 128, 256, 128, 0, 128, 256, 128, 1, 129, 257, 129, 1, 129, 257, 129}
1st Iteration:
For {0, 128, 256, 128, 0, 128, 256, 128} Total number of conflict misses = 2;
Total number of conflict misses = 2;
Similarly for {1, 129, 257, 129, 1, 129, 257, 129}, total number of conflict misses in set1 = 2
Total number of conflict misses in 1st iteration = 2 + 2 = 4
2nd iteration:
for {0, 128, 256, 128, 0, 128, 256, 128} Total number of conflict misses = 4.
Total number of conflict misses = 4.
Similarly for {1, 129, 257, 129, 1, 129, 257, 129}, total number of conflict misses in set1 = 4
Total Number of conflict misses in 2nd iteration = 4 + 4 = 8
Note that content of each set is same, before and after 2nd iteration. Therefore each of the remaining iterations will also have 8 conflict misses.
Therefore, overall conflict misses = 4 + 8 * 9 = 76.
Q24: Consider a two-level cache hierarchy with L1 and L2 caches. An application incurs 1.4 memory accesses per instruction on average. For this application, the miss rate of L1 cache 0.1, the L2 cache experiences, on average, 7 misses per 1000 instructions. The miss rate of L2 expressed correct to two decimal places is ___________. (2017 SET-1)
(a) 0.01
(b) 0.05
(c) 0.2
(d) 0.5
Ans: (b)
Sol: Assuming there are 1000 instructions for the ease of calculation, which means there are 7 memory reference misses from the L2 cache.
A cache experiences misses with memory references. Thus, it is essential to determine the counts of incoming memory references and the counts of memory references hitting or missing in order to calculate the cache hit rate or miss rate. Upon reading the question, it becomes apparent that the incoming memory references to the L2 cache are unknown, and we must derive this information using the provided L1 cache information.
Q25: Consider a system with 2 level cache. Access times of Level 1 cache, Level 2 cache and main memory are 1 ns, 10 ns, and 500 ns respectively. The hit rates of Level 1 and Level 2 caches are 0.8 and 0.9, respectively. What is the average access time of the system ignoring the search time within the cache? (2016)
(a) 13.0
(b) 12.8
(c) 12.6
(d) 12.4
Ans: (a)
Sol: By default we consider hierarchical access - because that is the common implementation and simultaneous access cache has great practical difficulty. But here the question is a bit ambiguous -- it says to ignore search time within the cache - usually search is applicable for an associative cache but here no such information given and so we can assume it is the indexing time in to the cache block.
Access time for hierarchical access,
= t1 + (1−h1) × t2 + (1−h1)(1−h2)tm
= 1 + 0.2 × 10 + 0.2 × 0.1 × 500
= 13ns.
Option A.
PS: We should follow simultaneous access only when explicitly mentioned in question as hierarchical access is the default in standard books.
Q26: A file system uses an in-memory cache to cache disk blocks.The miss rate of the cache is shown in the figure. The latency to read a block from the cache is 1 ms and to read a block from the disk is 10ms. Assume that the cost of checking whether a block exists in the cache is negligible. Available cache sizes are in multiples of 10MB. The smallest cache size required to ensure an average read latency of less than 6ms is_________ MB. (2016 SET-2)
The smallest cache size required to ensure an average read latency of less than 6ms is_________ MB. (2016 SET-2)
(a) 20
(b) 30
(c) 40
(d) 50
Ans: (b)
Sol: Look aside Cache Latency =1 ms
Main Memory Latency = 10 ms
- Lets try with 20 MB
Miss rate = 60% , Hit rate = 40%
Avg = 0.4(1) + 0.6(10)
= 0.4 + 6 = 6.4 ms > 6 ms - Next Take 30 MB
Miss rate = 40% , Hit rate = 60%
Avg = 0.6(1) + 0.4(10)
= 0.6 + 4 = 4.6 ms < 6 ms
So answer is 30 MB.
Q27: The width of the physical address on a machine is 40 bits. The width of the tag field in a 512KB 8-way set associative cache is ________ bits. (2016 SET-2)
(a) 21
(b) 23
(c) 24
(d) 31
Ans: (c)
Sol: Physical Address = 40
- Tag + Set + Block Offset = 40
- T + S + B = 40 → (1)
We have: Cache Size = number of sets × blocks per set × Block size
- 512 KB = number of sets × 8 × Block size
- Number of sets × Block size = 512/8 KB = 64 KB
- S + B = 16 → (2)
From (1), (2)
T = 24 bits (Ans)
Second way : Cache Size = 219
MM size = 240
This means, We need to map 240/219 = 221 Blocks to one line. And a set contain 23 lines.
Therefore, 224 blocks are mapped to one set.
Using Tag field, I need to identify which one block out of 224 blocks are present in this set.
Hence, 24 bits are needed in Tag field.
Q28: Consider a machine with a byte addressable main memory of 220 bytes, block size of 16 bytes and a direct mapped cache having 212 cache lines. Let the addresses of two consecutive bytes in main memory be (E201F)16 and (E2020)16. What are the tag and cache line address (in hex) for main memory address (E201F)16? (2015 SET-3)
(a) E, 201
(b) F, 201
(c) E, E20
(d) 2, 01F
Ans: (a)
Sol: Block size of 16 bytes means we need 4 offset bits. (The lowest 4 digits of memory address are offset bits)
Number of sets in cache (cache lines) = 212 so the next lower 12 bits are used for set indexing.
The top 4 bits (out of 20) are tag bits.
So, the answer is A.
Q29: Assume that for a certain processor, a read request takes 50 nanoseconds on a cache miss and 5 nanoseconds on a cache hit. Suppose while running a program, it was observed that 80% of the processor's read requests result in a cache hit. The average read access time in nanoseconds is __________. (2015 SET-2)
(a) 14
(b) 42
(c) 18
(d) 48
Ans: (a)
Sol: PS: Here instead of cache and main memory access times, time taken on a cache hit and miss are directly given in question. So,
Average Access Time = Hit Rate × Hit Time + Miss Rate × Miss Time
Q30: The memory access time is 1 nanosecond for a read operation with a hit in cache, 5 nanoseconds for a read operation with a miss in cache, 2 nanoseconds for a write operation with a hit in cache and 10 nanoseconds for a write operation with a miss in cache. Execution of a sequence of instructions involves 100 instruction fetch operations, 60 memory operand read operations and 40 memory operand write operations. The cache hit-ratio is 0.9. The average memory access time (in nanoseconds) in executing the sequence of instructions is __________. (2014 SET-3)
(a) 1.2
(b) 1.68
(c) 1.89
(d) 2.1
Ans: (b)
Sol: The question is to find the time taken for, Total number of instructions = 100 + 60 + 40 = 200
Total number of instructions = 100 + 60 + 40 = 200
Time taken for 100 fetch operations(fetch = read) = 100 ∗ ((0.9 ∗ 1) + (0.1 ∗ 5))
1 corresponds to time taken for read when there is cache hit = 140ns
0.9 is cache hit rate
Time taken for 60 read operations,
= 60 ∗ ((0.9∗1) + (0.1∗5))
= 84ns
Time taken for 40 write operations
= 40∗((0.9∗2) + (0.1∗10))
= 112ns
Here, 2 and 10 are the times taken for write when there is cache hit and no cache hit respectively.
So,the total time taken for 200 operations is,
= 140 + 84 + 112
= 336ns
Average time taken = time taken per operation
= 336/200
= 1.68ns
Q31: If the associativity of a processor cache is doubled while keeping the capacity and block size unchanged, which one of the following is guaranteed to be NOT affected? (2014 SET-2)
(a) Width of tag comparator
(b) Width of set index decoder
(c) Width of way selection multiplexor
(d) Width of processor to main memory data bus
Ans: (d)
Sol: If associativity is doubled, keeping the capacity and block size constant, then the number of sets gets halved. So, width of set index decoder can surely decrease - (B) is false.
Width of way-selection multiplexer must be increased as we have to double the ways to choose from- (C) is false
As the number of sets gets decreased, the number of possible cache block entries that a set maps to gets increased. So, we need more tag bits to identify the correct entry. So, (A) is also false.
(D) is the correct answer- main memory data bus has nothing to do with cache associativity- this can be answered without even looking at other options.
Q32: In designing a computer's cache system, the cache block (or cache line) size is an important Parameter. Which one of the following statements is correct in this context? (2014 SET-2)
(a) A smaller block size implies better spatial locality
(b) A smaller block size implies a smaller cache tag and hence lower cache tag overhead
(c) A smaller block size implies a larger cache tag and hence lower cache hit time
(d) A smaller block size incurs a lower cache miss penalty
Ans: (d)
Sol: (a) A smaller block size means during a memory access only a smaller part of near by addresses are brought to cache- meaning spatial locality is reduced.
(b) A smaller block size means more number of blocks (assuming cache size constant) and hence index bits go up and offset bits go down. But the tag bits remain the same.
(c) A smaller block size implying larger cache tag is true, but this can't lower cache hit time in any way.
(d) A smaller block size incurs a lower cache miss penalty. This is because during a cache miss, an entire cache block is fetched from next lower level of memory. So, a smaller block size means only a smaller amount of data needs to be fetched and hence reduces the miss penalty (Cache block size can go till the size of data bus to the next level of memory, and beyond this only increasing the cache block size increases the cache miss penalty).
Correct Answer: D
Q33: A 4-way set-associative cache memory unit with a capacity of 16 KB is built using a block size of 8 words. The word length is 32 bits. The size of the physical address space is 4 GB. The number of bits for the TAG field is _____ (2014 SET-2)
(a) 18
(b) 19
(c) 20
(d) 21
Ans: (c)
Sol: Number of sets = cache size/size of a set
Size of a set = blocksize × no. of blocks in a set
= 8 words × 4 (4-way set-associative)
= 8 × 4 × 4 (since a word is 32 bits = 4 bytes)
= 128 bytes.
So, number of sets = 16 KB/(128 B) = 128
Now, we can divide the physical address space equally between these 128 sets.
So, the number of bytes each set can access
= 4 GB/128
= 32 MB
= 32/4 = 8 M words = 1 M blocks. (220 blocks)
So, we need 20 tag bits to identify these 220 blocks.
Q34: An access sequence of cache block addresses is of length N and contains n unique block addresses. The number of unique block addresses between two consecutive accesses to the same block address is bounded above K. What is the miss ratio if the access sequence is passed through a cache of associativity A ≥ k exercising least-recently-used replacement policy? (2014 SET-1)
(a) n/N
(b) 1/N
(c) 1/A
(d) k/n
Ans: (a)
Sol: There are N accesses to cache.
Out of these n are unique block addresses.
Now, we need to find the number of misses. (min. n misses are guaranteed whatever be the access sequence due to n unique block addresses).
We are given that between two consecutive accesses to the same block, there can be only k unique block addresses. So, for a block to get replaced we can assume that all the next k block addresses goes to the same set (given cache is set-associative) which will be the worst case scenario (they may also go to a different set but then there is lesser chance of a replacement). Now, if associativity size is ≥ k, and if we use LRU (Least Recently Used) replacement policy, we can guarantee that these k accesses won't throw out our previously accessed cache entry (for that we need at least k accesses). So, this means we are at the best-cache scenario for cache replacement - out of N accesses we miss only n (which are unique and can not be helped from getting missed and there is no block replacement in cache). So, miss ratio is n/N.
PS: In question it is given "bounded above by k", which should mean k unique block accesses as k is an integer, but to ensure no replacement this must be 'k − 1'. Guess, a mistake in question.
Correct Answer: A.
Q35: How much speed do we gain by using the cache, when cache is used 80% of the time? Assume cache is faster than main memory. (2013)
(a) 5.27
(b) 2
(c) 4.16
(d) 6.09
Ans: (c)
Sol: Tcache << Tmemory
We can assume memory is accessed only on a cache miss (hierarchical memory access by default) and hence on cache miss we first access cache and then only main memory (both times are added here)
 Tcache/Tmemory = x, 0 < x ≤ 0.1 ( Since cache (say last level cache) is faster than memory by at least 10 times)
Tcache/Tmemory = x, 0 < x ≤ 0.1 ( Since cache (say last level cache) is faster than memory by at least 10 times)
Speed Gain = 1/(0.20 + x) ⇒ 3.33 ≤ Speed Gain < 5
I will go through 4.16.
Q36: In a k-way set associative cache, the cache is divided into v sets, each of which consists of k lines. The lines of a set are placed in sequence one after another. The lines in set s are sequenced before the lines in set (s+1). The main memory blocks are numbered 0 onwards. The main memory block numbered j must be mapped to any one of the cache lines from (2013)
(a) (j mod v)*k to (j mod v)*k + (k-1)
(b) (j mod v) to (j mod v) + (k-1)
(c) (j mod k) to (j mod k) + (v-1)
(d) (j mod k)*v to (j mod k)*v + (v-1)
Ans: (a)
Sol: Number of sets in cache = v.
The question gives a sequencing for the cache lines. For set 0, the cache lines are numbered 0, 1,.., k−1. Now for set 1, the cache lines are numbered k, k+1,... k + k−1 and so on.
So, main memory block j will be mapped to set (j mod v), which will be any one of the cache lines from (j mod v) ∗ k to (j mod v) ∗ k + (k−1).
(Associativity plays no role in mapping- k - way associativity means there are k spaces for a block and hence reduces the chances of replacement.)
Correct Answer: A
Q37: A computer has a 256 KByte, 4-way set associative, write back data cache with block size of 32 Bytes. The processor sends 32 bit addresses to the cache controller. Each cache tag directory entry contains, in addition to address tag, 2 valid bits, 1 modified bit and 1 replacement bit.
The size of the cache tag directory is (2012)
(a) 160 Kbits
(b) 136 Kbits
(c) 40 Kbits
(d) 32 Kbits
Ans: (a)
Sol: Total cache size = 256 KB
Cache block size = 32 Bytes
So, number of cache entries = 256 K/32 = 8 K
Number of sets in cache = 8 K/4 = 2 K as cache is 4-way associative.
So, log(2048) = 11 bits are needed for accessing a set. Inside a set we need to identify the cache entry.
Total number of distinct cache entries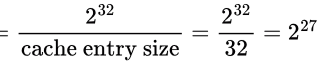 Out of this 227, each set will be getting only 227/211 = 216 possible distinct cache entries as we use the first 11 bits to identify a set. So, we need 16 bits to identify a cache entry in a set, which is the number of bits in the tag field.
Out of this 227, each set will be getting only 227/211 = 216 possible distinct cache entries as we use the first 11 bits to identify a set. So, we need 16 bits to identify a cache entry in a set, which is the number of bits in the tag field.
Size of cache tag directory = Size of tag entry × Number of tag entries
= 16 + (2 + 1 + 1) bits (2 valid, 1 modified, 1 replacement as given in question) × 8 K
= 208 = 160 Kbits
Not needed for this question, still:
Valid bit: Tells if the memory referenced by the cache entry is valid. Initially, when a process is loaded all entries are invalid. Only when a page is loaded, its entry becomes valid.
Modified bit: When processor writes to a cache location its modified bit is made 1. This information is used when a cache entry is replaced- entry 0 means no update to main memory needed. Entry 1 means an update is needed.
Correct Answer: A
Q38: A computer has a 256 KByte, 4-way set associative, write back data cache with block size of 32 Bytes. The processor sends 32 bit addresses to the cache controller. Each cache tag directory entry contains, in addition to address tag, 2 valid bits, 1 modified bit and 1 replacement bit.
The number of bits in the tag field of an address is (2012)
(a) 11
(b) 14
(c) 16
(d) 27
Ans: (c)
Sol: Total cache size = 256 KB
Cache block size = 32 Bytes
So, number of cache entries = 256 K/32 = 8 K
Number of sets in cache = 8 K/4 = 2 K as cache is 4-way associative.
So, log(2048)=11 bits are needed for accessing a set. Inside a set we need to identify the cache entry.
No. of memory block possible = Memory size/Cache block size
= 232/32 = 227.
So, no. of memory block that can go to a single cache set = 227/211 = 216.
So, we need 16 tag bits along with each cache entry to identify which of the possible 216 blocks is being mapped there.
Correct Answer: C
Q39: The search concept used in associative memory is (2011)
(a) Parallel search
(b) Sequential search
(c) Binary search
(d) Selection search
Ans: (a)
Sol: Search in associative memory is parallel. For k-way associativity we can have k comparators which compares the tag bits of 'k' blocks in parallel. We can't increase 'k' beyond a limit due to hardware limitation.
Q40: Consider a direct mapped cache with 64 blocks and a block size of 16 bytes. To what block number does the byte address 1206 map to (2011)
(a) does not map
(b) 6
(c) 11
(d) 54
Ans: (c)
Sol: Block size = 16B
Total No of Block = 64
Memory block Number = Byte address/Block Size
= 1206/16
= 75
Now we have to find a cache block number related to memory block number.
So In Direct Mapped cache,
Cache block Number = Memory block Number mod(Total Number of a block in cache)
= 75 mod 64
= 11
So option C is correct.
Q41: An 8KB direct mapped write-back cache is organized as multiple blocks, each of size 32-bytes. The processor generates 32-bit addresses. The cache controller maintains the tag information for each cache block comprising of the following. 1 Valid bit 1 Modified bit As many bits as the minimum needed to identify the memory block mapped in the cache. What is the total size of memory needed at the cache controller to store metadata (tags) for the cache? (2011)
(a) 4864 bits
(b) 6144 bits
(c) 6656 bits
(d) 5376 bits
Ans: (d)
Sol: Number of cache blocks = cache size/size of block
= 8 KB/32 B
= 256
So, we need 8-bits for indexing the 256 blocks of the cache. And since a block is 32 bytes we need 5 WORD bits to address each byte. So, out of the remaining 19-bits (32 - 8 - 5) should be tag bits.
So, a tag entry size = 19+1(valid bit)+1(modified bit) = 21 bits.
Total size of metadata = 21 × Number of cache blocks
= 21 × 256
= 5376 bits
Correct Answer: D
Q42: A computer system has an L1 cache, an L2 cache, and a main memory unit connected as shown below. The block size in L1 cache is 4 words. The block size in L2 cache is 16 words. The memory access times are 2 nanoseconds. 20 nanoseconds and 200 nanoseconds for L1 cache, L2 cache and main memory unit respectively. When there is a miss in both L1 cache and L2 cache, first a block is transferred from main memory to L2 cache, and then a block is transferred from L2 cache to L1 cache. What is the total time taken for these transfers? (2010)
When there is a miss in both L1 cache and L2 cache, first a block is transferred from main memory to L2 cache, and then a block is transferred from L2 cache to L1 cache. What is the total time taken for these transfers? (2010)
(a) 222 nanoseconds
(b) 888 nanoseconds
(c) 902 nanoseconds
(d) 968 nanoseconds
Ans: (c)
Sol: The transfer time should be 4 ∗ 200 + 20 = 820 ns. But this is not in option. So, I assume the following is what is meant by the question.
L2 block size being 16 words and data width between memory and L2 being 4 words, we require 4 memory accesses(for read) and 4 L2 accesses (for store). Now, we need to send the requested block to L1 which would require one more L2 access (for read) and one L1 access (for store). So, total time
= 4 ∗ (200 + 20) + (20 + 2)
= 880 + 22
= 902 ns
Correct Answer: C
Q43: A computer system has an L1 cache, an L2 cache, and a main memory unit connected as shown below. The block size in L1 cache is 4 words. The block size in L2 cache is 16 words. The memory access times are 2 nanoseconds. 20 nanoseconds and 200 nanoseconds for L1 cache, L2 cache and main memory unit respectively. When there is a miss in L1 cache and a hit in L2 cache, a block is transferred from L2 cache to L1 cache. What is the time taken for this transfer? (2010)
When there is a miss in L1 cache and a hit in L2 cache, a block is transferred from L2 cache to L1 cache. What is the time taken for this transfer? (2010)
(a) 2 nanoseconds
(b) 20 nanoseconds
(c) 22 nanoseconds
(d) 88 nanoseconds
Ans: (c)
Sol: Ideally the answer should be 20 ns as it is the time to transfer a block from L2 to L1 and this time only is asked in question. But there is confusion regarding access time of L2 as this means the time to read data from L2 till CPU but here we need the time till L1 only. So, I assume the following is what is meant by the question.
A block is transferred from L2 to L1. And L1 block size being 4 words (since L1 is requesting we need to consider L1 block size and not L2 block size) and data width being 4 bytes, it requires one L2 access (for read) and one L1 access (for store). So, time = 20+2 = 22 ns.
Correct Answer: C.
|
20 videos|86 docs|48 tests
|
FAQs on Previous Year Questions: Cache Memory - Computer Architecture & Organisation (CAO) - Computer Science Engineering (CSE)
| 1. What is cache memory in a computer system? |  |
| 2. How does cache memory improve the performance of a computer system? |  |
| 3. What are the different levels of cache memory in a typical computer system? |  |
| 4. How is cache memory organized in a computer system? |  |
| 5. What are the common cache memory replacement policies used in computer systems? |  |
|
20 videos|86 docs|48 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|

















