Previous Year Questions- Calculus - 1 | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
Q1: Let f(t) be a real-valued function whose second derivative is positive for −∞
ltt
lt ∞. Which of the following statements is/are always true? (2024)
(a) f(t) has at least one local minimum.
(b) f(t) cannot have two distinct local minima.
(c) f(t) has at least one local maximum.
(d) The minimum value of f(t) cannot be negative.
Ans: (b)
Sol: 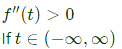 ⇒ f(t) is a parabola open upwards. So, it has only one minima at its stationary point.
⇒ f(t) is a parabola open upwards. So, it has only one minima at its stationary point.
∴ f(t) cannot have two distinct local minima.
Q2: Consider a vector 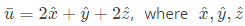 represent unit vector along the coordinate axes x, y, z respectively. The directional derivative of the function f(x, y, z) = 2 ln (xy) + ln(yz) + 3ln(xz) at the point (x, y, z) = (1, 1, 1) in the direction of
represent unit vector along the coordinate axes x, y, z respectively. The directional derivative of the function f(x, y, z) = 2 ln (xy) + ln(yz) + 3ln(xz) at the point (x, y, z) = (1, 1, 1) in the direction of 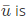 (2024)
(2024)
(a) 0
(b) 7/(5√2)
(c) 7
(d) 21
Ans: (c)
Sol: We know that: directional derivative of 'f' at P(1, 1, 1) in the direction of 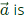 is given by
is given by
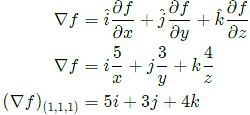
∴ Directional derivative 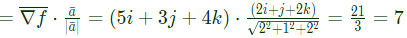
Q3: The closed curve shown in the figure is described by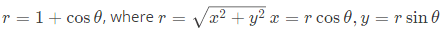 The magnitude of the line integral of the vector field
The magnitude of the line integral of the vector field 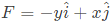 around the closed curve is ___(Round off to 2 decimal places). 2023
around the closed curve is ___(Round off to 2 decimal places). 2023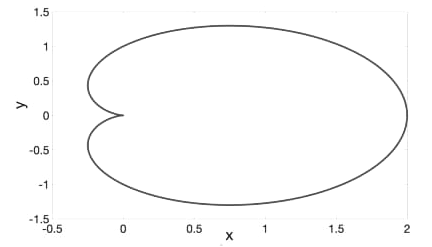
(a) 9.42
(b) 6.36
(c) 2.45
(d) 7.54
Ans: (a)
Sol: 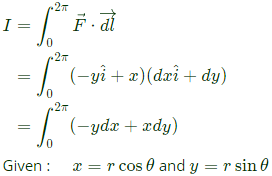
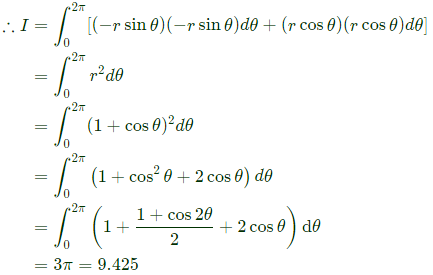
Q4: Consider the following equation in a 2-D realspace.
∣x1∣p + ∣x2∣p = 1 for p > 0
Which of the following statement(s) is/are true. (2023)
(a) When p = 2, the area enclosed by the curve is π.
(b) When p tends to ∞, the area enclosed by the curve tends to 4.
(c) When p tends to 0 , the area enclosed by the curve is 1.
(d) When p = 1, the area enclosed by the curve is 2.
Ans: (a), (b), (d)
Sol: Check option (A),
put P = 2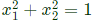 Which is equation of circle whose radius is 1 .
Which is equation of circle whose radius is 1 .
∴ Area = πr2 = π
Check option (B),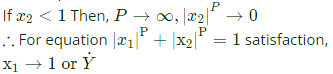 Curve :
Curve :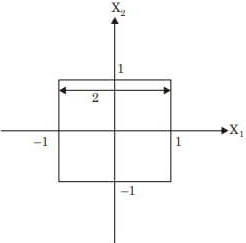 ∴ Area tends to 4 .
∴ Area tends to 4 .
Check option (D),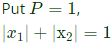 Curve:
Curve: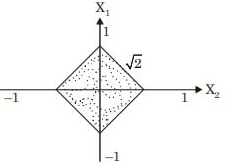
∴ Area of curve (square) =(√2)2 = 2
Q5: One million random numbers are generated from a statistically stationary process with a Gaussian distribution with mean zero and standard deviation σ0.
The σ0 is estimated by randomly drawing out 10,000 numbers of samples (xn). The estimates 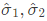 are computed in the following two ways.
are computed in the following two ways.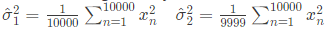 Which of the following statements is true? (2023)
Which of the following statements is true? (2023)
(a) 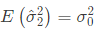
(b) 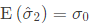
(c) 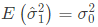
(d) 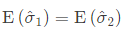
Ans: (c)
Sol: We know,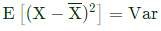 Given,
Given, 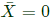
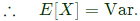 We have,
We have,
Standard deviation, 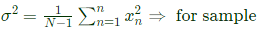 and
and 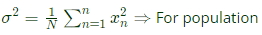
Here, we take samples from 106 numbers.
∴ 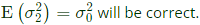
Q6: In the figure, the vectors u and v are related as: Au = v by a transformation matrix A. The correct choice of A is (2023)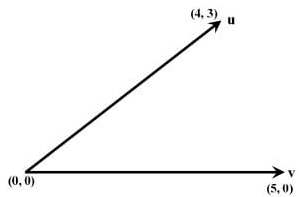
(a) 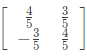
(b) 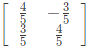
(c) 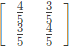
(d)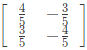
Ans: (a)
Sol: Given :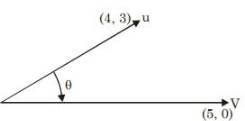
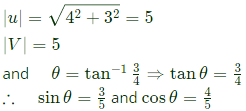 For clockwise relation by θ, transformation matrix,
For clockwise relation by θ, transformation matrix,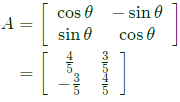 [∵ F or clockwise θ → N egative]
[∵ F or clockwise θ → N egative]
Q7: For a given vector w = [1 2 3]⊤, the vector normal to the plane defined by w⊤x = 1 is (2023)
(a) [−2 −2 2]T
(b) [3 0 −1]T
(c) [3 2 1]T
(d) [1 2 3]T
Ans: (d)
Sol: Given, WT = 1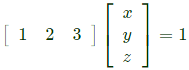 We have, vector normal to the plane = ∇F
We have, vector normal to the plane = ∇F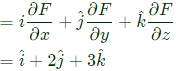 ∴ Normal vector = [1 2 3]T
∴ Normal vector = [1 2 3]T
Q8: Let 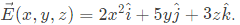 The value of
The value of 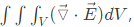 where V is the volume enclosed by the unit cube defined by
where V is the volume enclosed by the unit cube defined by 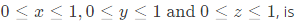 (2022)
(2022)
(a) 3
(b) 8
(c) 10
(d) 5
Ans: (c)
Sol: Divergence of 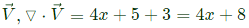
Now,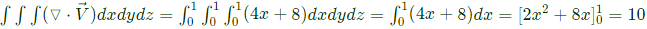
Q9: Let  Then f(x) decreases in the interval (2022)
Then f(x) decreases in the interval (2022)
(a) x ∈ (1, 2)
(b) x ∈ (2, 3)
(c) x ∈ (0, 1)
(d) x ∈ (0.5, 1)
Ans: (a)
Sol: The function is decreasing, if f′(x) < 0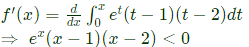 It is possible in between 1 & 2. Hence x ∈ (1, 2)
It is possible in between 1 & 2. Hence x ∈ (1, 2)
Q10: In the open interval (0, 1), the polynomial p(x) = x4 − 4x3 + 2 has (2021)
(a) two real roots
(b) one real root
(c) three real roots
(d) no real roots
Ans: (b)
Sol: 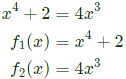 It is clear that point of intersection of these graphs is solution (or) root of p(x) = 0
It is clear that point of intersection of these graphs is solution (or) root of p(x) = 0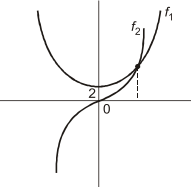 According to intermediate value theorem
According to intermediate value theorem
P(0) and P(1) are having opposite signs
∴ a root of p(x) = 0 in (0, 1)
and also from graph, there is only one point of intersection
Hence exactly one real root exists in (0, 1) .
Q11: Suppose the circles x2 + y2 = 1 and (x − 1)2 + (y − 1)2 = r2 intersect each other orthogonally at the point (u, v). Then u + v = _______. (2021)
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (b)
Sol: If two curves cut orthogonally then product of slopes = −1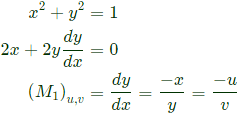
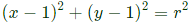
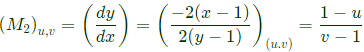
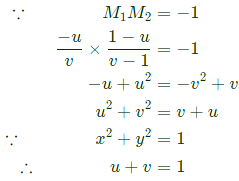
Q12: Let f(x) be a real-valued function such that f′(x0) = 0 for some x0 ∈ (0, 1), and f′′(x) > 0 for all x ∈ (0, 1). Then f(x) has (2021)
(a) no local minimum in (0,1)
(b) one local maximum in (0,1)
(c) exactly one local minimum in (0,1)
(d) two distinct local minima in (0,1)
Ans: (c)
Sol: x0 ∈ (0, 1), where f(x) = 0 is stationary point
and f′′(x) > 0, ∀x ∈ (0,1)
So f′(x0) = 0
and 𝑓′(0) > 0, where x0 ∈ (0, 1)
Hence, f(x) has exactly one local minima in (0, 1)
Q13: Let ax and ay be unit vectors along x and y directions, respectively. A vector function is given by F = axy − ayx
The line integral of the above function 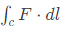 along the curve C, which follows the parabola y = x2 as shown below is _______ (rounded off to 2 decimal places). (2020)
along the curve C, which follows the parabola y = x2 as shown below is _______ (rounded off to 2 decimal places). (2020) (a) 2
(a) 2
(b) -2
(c) 3
(d) -3
Ans: (d)
Sol: 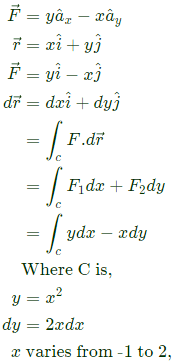
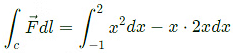
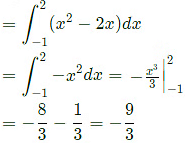 = -3
= -3
Q14: If A = 2xi + 3yj + 4zk and u = x2 + y2 + z2, then div(uA) at (1, 1, 1) is____ (2019)
(a) 15
(b) 45
(c) 30
(d) 60
Ans: (b)
Sol: 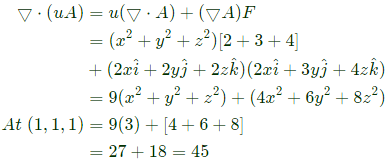
Q15: If f = 2x3 + 3y2 + 4z, the value of line integral ∫cgrad f⋅dr evaluated over contour C formed by the segments (-3, -3, 2) → (2, -3, 2) → (2, 6, 2) → (2, 6, -1) is_______ (2019)
(a) 112
(b) 139
(c) 156
(d) 186
Ans: (b)
Sol: 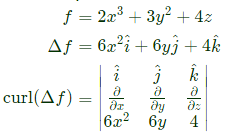
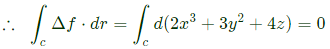
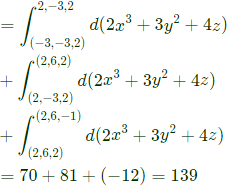
Q16: Let f(x) = 3x3 − 7x2 + 5x + 6. The maximum value of f(x) over the interval [0, 2] is _______ (up to 1 decimal place). (2018)
(a) 8.2
(b) 12.0
(c) 16.2
(d) 18.7
Ans: (b)
Sol: 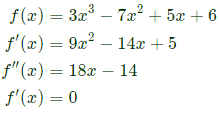 9x2 − 14x + 5 = 0
9x2 − 14x + 5 = 0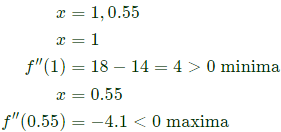 Maximum [f(0), f′(0.55), f(2)]
Maximum [f(0), f′(0.55), f(2)]
Maximum [6, 7.13, 12] = 12
Q17: As shown in the figure, C is the arc from the point (3, 0) to the point (0, 3) on the circle x2 + y2 = 9. The value of the integral 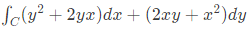 is _____ (up to 2 decimal places). (2018)
is _____ (up to 2 decimal places). (2018)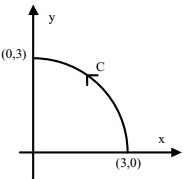
(a) 0
(b) 0.11
(c) 0.25
(d) 0.66
Ans: (a)
Sol: 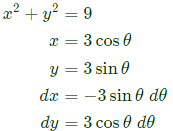 θ varies from 0 to π/2
θ varies from 0 to π/2
Q18: Let f be a real-valued function of a real variable defined as f (x) = x-[x], where [x] denotes the largest integer less than or equal to x. The value of 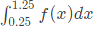 is _______ (up to 2 decimal places). (2018)
is _______ (up to 2 decimal places). (2018)
(a) 0.25
(b) 0.5
(c) 0.75
(d) 0.85
Ans: (b)
Sol: 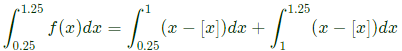
Q19: The value of the directional derivative of the function ϕ(x, y, z) = xy2+yz2+zx2 at the point (2,-1,1) in the direction of the vector p = i + 2j + 2k is (2018)
(a) 1
(b) 0.95
(c) 0.93
(d) 0.9
Ans: (a)
Sol: 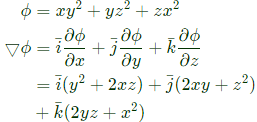
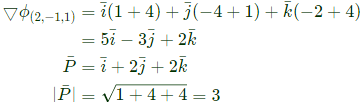 THe directional derivative of f(x, y, z) at (2, -1, 1) in the direction of
THe directional derivative of f(x, y, z) at (2, -1, 1) in the direction of 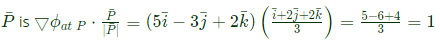
Q20: Let f be a real-valued function of a real variable defined as f(x) = x2 for x > 0, and f(x) = −x2 for x < 0. Which one of the following statements is true? (2018)
(a) f(x) is discontinuous at x = 0
(b) f(x) is continuous but not differentiable at x = 0
(c) f(x) is differentiable but its first derivative is not continuous at x = 0
(d) f(x) is differentiable but its first derivative is not differentiable at x = 0
Ans: (d)
Sol: 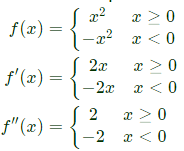 The first derivation of f (i.e) f'(x) is not derivable at x = 0.
The first derivation of f (i.e) f'(x) is not derivable at x = 0.
Q21: Let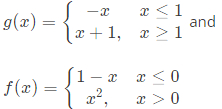 Consider the composition of f and g, i.e., (f ∘ g)(x) = f(g(x)). The number of discontinuities in (f ∘ g)(x) present in the interval (−∞, 0) is: (SET-2(2017))
Consider the composition of f and g, i.e., (f ∘ g)(x) = f(g(x)). The number of discontinuities in (f ∘ g)(x) present in the interval (−∞, 0) is: (SET-2(2017))
(a) 0
(b) 1
(c) 2
(d) 4
Ans: (a)
Sol: f(x) =1− x ; x< 0
g(x) = -x; x < 0
(Noth are continous for x < 0)
Therefore, fog(x) is continous for x < 0
The composite function of two continous function is always continous . Therefore the number of discontinuities are zero.
Q22: Consider a function f (x, y, z) given by f(x, y, z) = (x2 + y2 − 2z2)(y2 + z2) The partial derivative of this function with respect to x at the point, x = 2, y = 1 and z = 3 is ________ (SET-2(2017))
(a) 13
(b) 40
(c) 36
(d) 4
Ans: (b)
Sol: 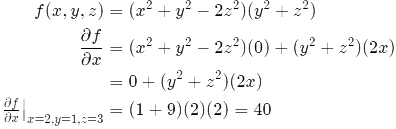
Q23: A function f(x) is defined as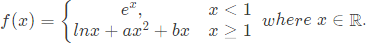 Which one of the following statements is TRUE? (SET-1(2017))
Which one of the following statements is TRUE? (SET-1(2017))
(a) f(x) is NOT differentiable at x=1 for any values of a and b.
(b) f(x) is differentiable at x = 1 for the unique values of a and b
(c) f(x) is differentiable at x = 1 for all values of a and b such that a + b = e
(d) f(x) is differentiable at x = 1 for all values of a and b.
Ans: (b)
Sol: 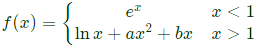 At x = 1,
At x = 1,
L.H.S = R.H.S
e = a + b ...(i)
At x = 1, f'(x) exists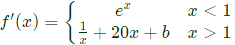 At x = 1,
At x = 1,
L.H.S = R.H.S
e = 1 + 2a + b
2a + b = e - 1 ...(ii)
From equation (i) and (ii),
a = -1
b = e + 1
f(x) is differentiable at x = 1 for unique value of a and b.
Q24: Let 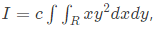 where R is the region shown in the figure and c = 6 × 10−4. The value of I equals________ (SET-1(2017))
where R is the region shown in the figure and c = 6 × 10−4. The value of I equals________ (SET-1(2017))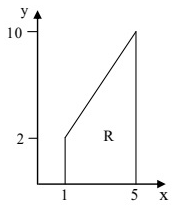 (a) 0.5
(a) 0.5
(b) 1
(c) 2
(d) 3
Ans: (b)
Sol: 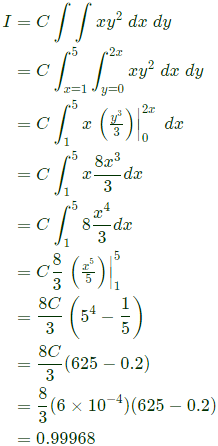
Q25: The value of the line integral 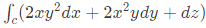 along a path joining the origin (0, 0, 0) and the point (1, 1, 1) is (SET-2(2016))
along a path joining the origin (0, 0, 0) and the point (1, 1, 1) is (SET-2(2016))
(a) 0
(b) 2
(c) 4
(d) 6
Ans: (b)
Sol: 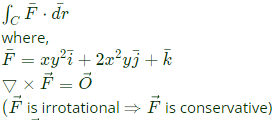
Q26: The value of the integral  over the contour |z| = 1, taken in the anti-clockwise direction, would be (SET-1(2016))
over the contour |z| = 1, taken in the anti-clockwise direction, would be (SET-1(2016))
(a) 
(b)
(c) 24/13
(d) 12/13
Ans: (b)
Sol: Singlarilies, Z = 1/2, 2 ± i
Only Z = 1/2 lies inside C
By residue theorem,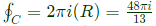 Residue at 1/2
Residue at 1/2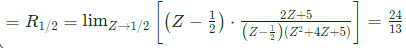
Q27: A function y(t), such that y(0) = 1 and y(1) = 3𝑒−1, is a solution of the differential equation 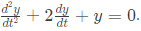 Then y(2) is (SET-1(2016))
Then y(2) is (SET-1(2016))
(a) 5e−1
(b) 5e−2
(c) 7e−2
(d) 7e−2
Ans: (b)
Sol: Auxiliary equation,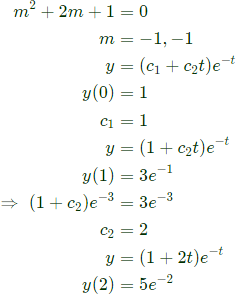
Q28: The maximum value attained by the function f(x) = x(x − 1)(x − 2) in the interval [1, 2] is _____. (SET-1(2016))
(a) 0
(b) 1
(c) 2
(d) 4
Ans: (a)
Sol: 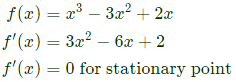 stationary points are 1 + 1/√3
stationary points are 1 + 1/√3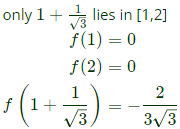 Maximum value is 0.
Maximum value is 0.
Q29: The volume enclosed by the surface f(x, y) = ex over the triangle bounded by the lines x = y; x = 0; y = 1 in the xy plane is ______. (SET-2(2015))
(a) 0
(b) 0.25
(c) 0.56
(d) 0.71
Ans: (d)
Sol: 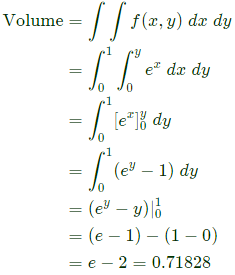
Q30: If a continuous function f(x) does not have a root in the interval [a, b], then which one of the following statements is TRUE? (SET-1 (2015))
(a) f(a)⋅f(b) = 0
(b) f(a)⋅f(b) < 0
(c) f(a)⋅f(b) > 0
(d) f(a)/f(b) ≤ 0
Ans: (c)
Sol: Intermediate value theorem states that if a function is continious and f(a)⋅f(b) < 0, then surely there is a root in (a, b). The contrapositive of this theorem is that if a function is continious and has no root in (a, b) then surely f(a)⋅f(b) ≥ 0. But since it is given that there is no root in the closed interval [a, b] it means f(a)⋅f(b) ≠ 0.
So surely f(a)⋅f(b) > 0 which is choise(C).
|
44 videos|109 docs|58 tests
|
FAQs on Previous Year Questions- Calculus - 1 - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. What is the fundamental theorem of calculus? |  |
| 2. How can calculus be applied in electrical engineering? |  |
| 3. What are some common applications of calculus in electrical engineering? |  |
| 4. How can integration be used in electrical engineering? |  |
| 5. How does differentiation play a role in electrical engineering? |  |
















