Class 9 Maths - Circles Previous Year Questions
Very Short Answer Type Questions
Q1. If points A, B and C are such that AB ⊥ BC and AB = 12 cm, BC = 16 cm. Find the radius of the circle passing through the points A, B and C. [2025]
Sol:
∵ AB ⊥ BC
∴ ∠B = 90° [Angle in a semicircle]
⇒ AC is a diameter
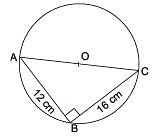
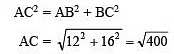
AC = 20
Radius = 10cm
Q2. The angles subtended by a chord at any two points of a circle are equal. Write true or false for the above statement and justify your answer. [2023]
Sol:
False. If two points lie in the same segment only, then the angles will be equal otherwise they are not equal.
Short Answer Type Questions
Q1. In the figure AOC is a diameter of the circle and arc AXB = (1/2) arc BYC. Find ∠BOC. [2025]
Sol:
∵ arc AXB = (1/2)arc BYC
∴ ∠AOB = (1/2) ∠BOC
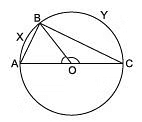
Also ∠AOB + ∠BOC = 180°
⇒ (1/2)∠BOC + ∠BOC = 180°
⇒ (3/2) ∠BOC = 180°
⇒ ∠BOC = (1/2) × 180° = 120°
Q2. In the figure ∠ABC = 45°. Prove that OA ⊥ OC. [2024]
Sol:
Since the angle subtended at the centre by an arc is double the angle subtended by it at any other point on the remaining part of the circle.
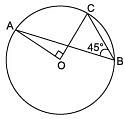
∴ ∠ABC =(1/2)∠AOC
⇒ ∠AOC = 2 ∠ABC = 2 × 45° = 90° [∵ ∠ABC = 45°]
Thus, OA ⊥ OC.
Q3. In the adjoining figure, O is the centre of the circle. Find the length of AB. [2023]
Sol:
Since chord AB and chord CD subtend equal angles at the centre,
i.e. ∠ AOB = ∠ COD [Each = 60°]
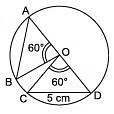
∴ Chord AB = Chord CD
⇒ Chord AB = 5 cm [∵ Chord CD = 5 cm]
Thus, the required length of chord AB is 5 cm.
Q4. In the adjoining figure, O is the centre of the circle and OP = OQ. If AP = 4 cm, then find the length of CD. [2022]
Sol:
∵ OP = OQ
∴ Chord AB and chord CD are equidistant from the centre.
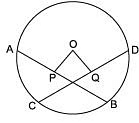
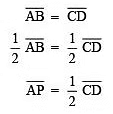
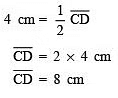
Thus, the required length of CD is 8 cm.
Q5. If O is the centre of the circle, then find the value of x. [2021]
Sol:
∵ AOB is a diameter.
∴ ∠ AOC + ∠ COB = 180° [Linear pairs]
⇒ 130° + ∠ COB = 180°
⇒ ∠ COB = 180° - 130° = 50°
Now, the arc CB is subtending ∠COB at the centre and ∠CDB at the remaining part.
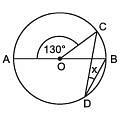
∴ ∠ CDB = (1/2)∠COB
⇒ ∠ CDB = (1/2)x 50° = 25°
Thus, the measure of x = 25°
Q6. The radius of a circle is 17 cm. A chord of length 30 cm is drawn. Find the distance of the chord from the centre. [2020]
Sol:
Length of chord AB = 30 cm.
Since, OP ⊥ AB
∴ P is the mid-point of AB.
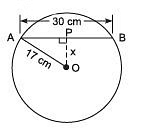
AP = (1/2)AB =(1/2) x 30 cm = 15 cm
Now, in right ΔAPO, AO2 = AP2 + OP2
⇒ 172 = 152 + OP2
∴ OP2 = 172 - 152 = (17 - 15)(17 + 15)
= 2 x 32 = 64
⇒ OP = 64 = 8 cm
∴ The distance of the chord AB from the centre O is 8 cm.
Long Answer Type Questions
Q1. An equilateral triangle is inscribed in a circle. Find the radius of the circle. [2024]
Sol:
Let ABC be an equilateral triangle such that AB = BC = AC = 9 cm (each)
Let us draw a median AD corresponding to BC.
∴ BD =(1/2) BC
⇒ BD = (1/2) x 9 cm = (9/2)cm
Also, AD ⊥ BC [∵ O is the centre of the circle]
Now, in right ΔADB,
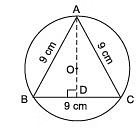
AD2 = AB2 - BD2
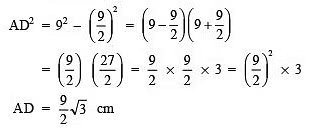
Since, in an equilateral triangle, the centroid and circumcentre coincide.
∴ AO: OD = 2:1
⇒ 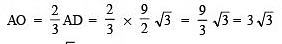
⇒ Radius = 3√3 cm
Thus, the required radius = 3√3 cm
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths - Circles Previous Year Questions
| 1. What are the basic properties of circles that students should know? |  |
| 2. How do you calculate the area and circumference of a circle? |  |
| 3. What is the relationship between the diameter and the radius of a circle? |  |
| 4. What are the different types of angles formed by intersecting chords in a circle? |  |
| 5. How do circles relate to other geometric shapes in terms of properties and formulas? |  |





















