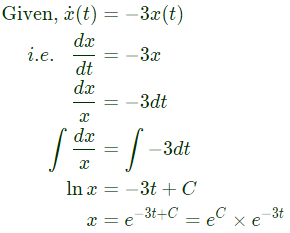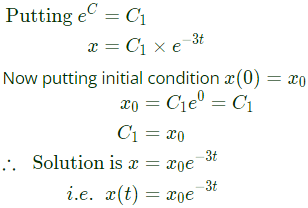Additional Information about Previous Year Questions- Differential Equations for Electrical Engineering (EE) Preparation
Previous Year Questions- Differential Equations Free PDF Download
The Previous Year Questions- Differential Equations is an invaluable resource that delves deep into the core of the Electrical Engineering (EE) exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Previous Year Questions- Differential Equations now and kickstart your journey towards success in the Electrical Engineering (EE) exam.
Importance of Previous Year Questions- Differential Equations
The importance of Previous Year Questions- Differential Equations cannot be overstated, especially for Electrical Engineering (EE) aspirants.
This document holds the key to success in the Electrical Engineering (EE) exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Previous Year Questions- Differential Equations Notes
Previous Year Questions- Differential Equations Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Previous Year Questions- Differential Equations.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Previous Year Questions- Differential Equations Notes on EduRev are your ultimate resource for success.
Previous Year Questions- Differential Equations Electrical Engineering (EE)
The "Previous Year Questions- Differential Equations Electrical Engineering (EE) Questions" guide is a valuable resource for all aspiring students preparing for the
Electrical Engineering (EE) exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Previous Year Questions- Differential Equations on the App
Students of Electrical Engineering (EE) can study Previous Year Questions- Differential Equations alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Previous Year Questions- Differential Equations,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Previous Year Questions- Differential Equations is prepared as per the latest Electrical Engineering (EE) syllabus.

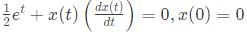

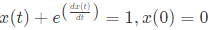
 ∴ f(x) is differential and f′(x) is continuous but f′(x) is not continuous.
∴ f(x) is differential and f′(x) is continuous but f′(x) is not continuous.
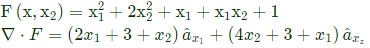

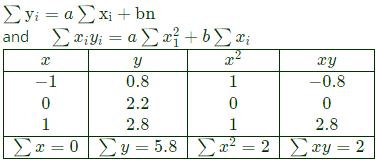 From eqn. (1), we get
From eqn. (1), we get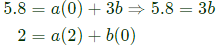 ⇒ a = 1
⇒ a = 1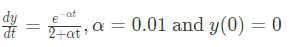 (2023)
(2023) 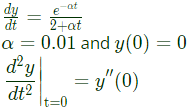
 We know,
We know,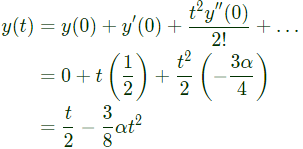
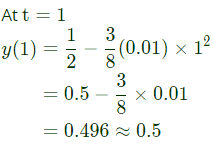
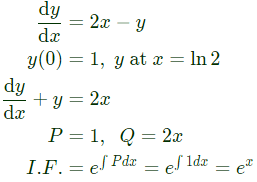 Solution,
Solution,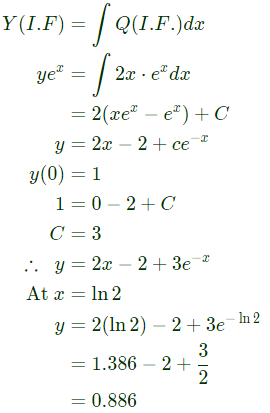
 is known as (2019)
is known as (2019)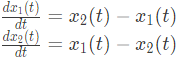 The initial conditions are such that
The initial conditions are such that 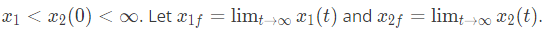 Which one of the following is true? (2018)
Which one of the following is true? (2018)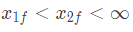
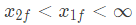
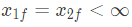
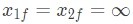
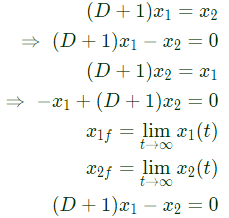
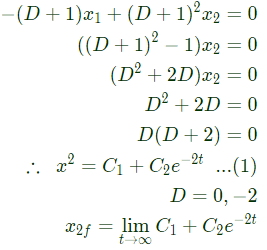
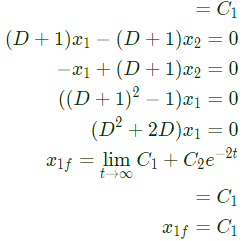
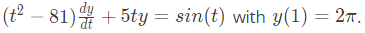 There exists a unique solution for this differential equation when t belongs to the interval (SET-1 (2017))
There exists a unique solution for this differential equation when t belongs to the interval (SET-1 (2017))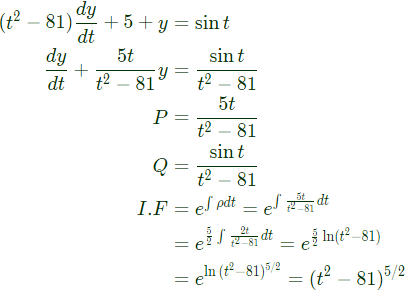
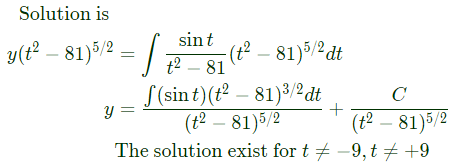 Only option (A) not cover 9 and -9. Hence it is correct.
Only option (A) not cover 9 and -9. Hence it is correct.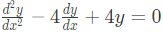 with initial conditions y(0) = 0 and
with initial conditions y(0) = 0 and 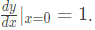 Then the value of y(1) is _________. (SET-2 (2016))
Then the value of y(1) is _________. (SET-2 (2016))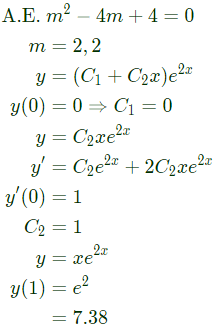
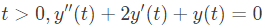 with initial conditions y(0) = 0 and y'(0) = 1, is (u(t) denotes the unit step function), (SET-2 (2016))
with initial conditions y(0) = 0 and y'(0) = 1, is (u(t) denotes the unit step function), (SET-2 (2016))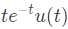

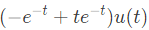
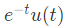

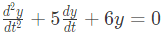 is such that y(0) = 2 and y (1) =
is such that y(0) = 2 and y (1) =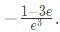 The value of (dy/dt) (0) is _______ (SET-1 (2015))
The value of (dy/dt) (0) is _______ (SET-1 (2015))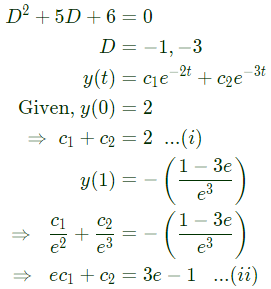
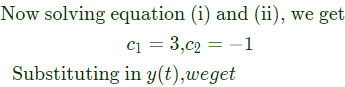
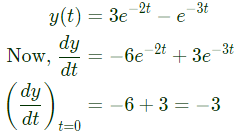
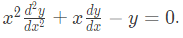 Which of the following is a solution to this differential equation for x > 0 ? (SET-2 (2014))
Which of the following is a solution to this differential equation for x > 0 ? (SET-2 (2014))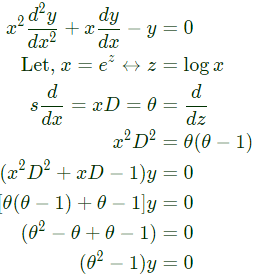
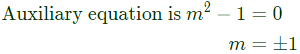
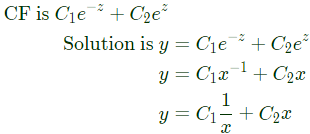 One independent solution is (1/x)
One independent solution is (1/x)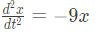 with initial conditions x(0) = 1 and
with initial conditions x(0) = 1 and 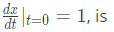 (SET-1 (2014))
(SET-1 (2014))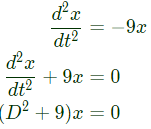 Auxiliary equation is m2+9 = 0
Auxiliary equation is m2+9 = 0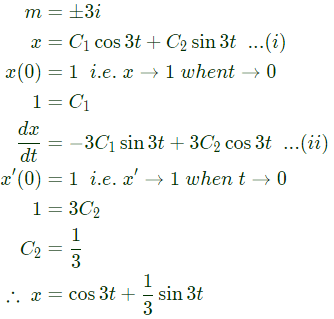
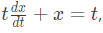 is (2012)
is (2012)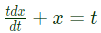 with initial condition x(t) = 1/2 which is same as
with initial condition x(t) = 1/2 which is same as 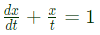
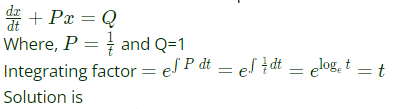
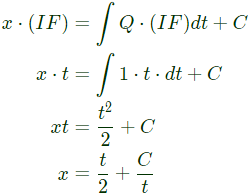
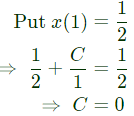 So, x = (t/2) is the solution.
So, x = (t/2) is the solution.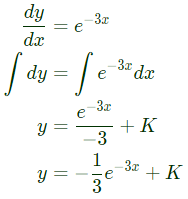
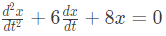 with initial conditions x(0) = 1 and
with initial conditions x(0) = 1 and 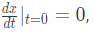 the solution is (2010)
the solution is (2010)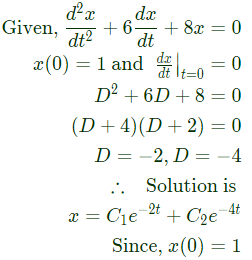
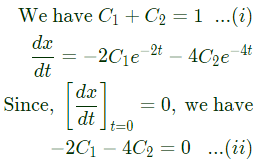
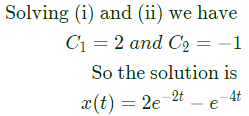
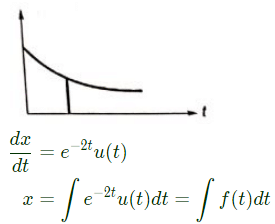
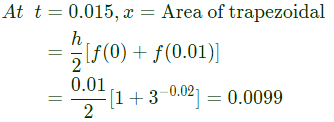
 the solution x(t) approaches which of the following values as t → ∞? (2005)
the solution x(t) approaches which of the following values as t → ∞? (2005)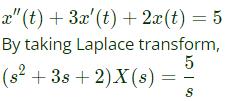

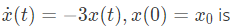 (2005)
(2005)