Previous Year Questions: Functions | Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE) PDF Download
Q1: Let A and B be non-empty finite sets such that there exist one-to-one and onto functions (i) from A to B and (ii) from A × A to A ∪ B. The number of possible values of ∣A∣ is ___ (2024 SET-1)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
Sol: There exist one-to-one and onto function between X and Y implies |X| = |Y|.
Hence, |A| = |B| and |A|2 = |A| + |B| − |A ∩ B|.
Can |A| = 1?
Yes, when |A| = |B| = |A ∩ B| = 1.
Can |A| = 2?
Yes, when |A| = |B| = 2, |A ∩ B| = 0.
For larger values of |A|, |A|2 > |A| + |B|.
Therefore, only 2 values are possible for |A|.
Q2: Let 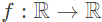 be a function such that f(x) = max{x, x3}, x ∈
be a function such that f(x) = max{x, x3}, x ∈ 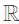 , where
, where 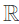 is the set of all real numbers. The set of all points where f(x) is NOT differentiable is (2024 SET-1)
is the set of all real numbers. The set of all points where f(x) is NOT differentiable is (2024 SET-1)
(a) −1, 1, 2
(b) −2, −1, 1
(c) 0, 1
(d) -1, 0, 1
Ans: (d)
Sol: If we try to plot the function f(x) = max(x, x3), it will look something like the image below as we can clearly see the funtion is continuous everywhere but it is not differentiable at {-1, 0, 1}
Q3: Let f : A → B be an onto (or surjective) function, where A and B are nonempty sets.
Define an equivalence relation ∼ on the set A as
a1 ∼ a2 if f(a1) = f(a2),
where a1, a2 ∈ A. Let ε = {[x]: x ∈ A} be the set of all the equivalence classes under∼. Define a new mapping F: ε → B as
F([x]) = f(x), for all the equivalence classes [x] in ε
Which of the following statements is/are TRUE? (2023)
(a) F is NOT well-defined.
(b) F is an onto (or surjective) function.
(c) F is a one-to-one (or injective) function.
(d) F is a bijective function.
Ans: (b, c, d)
Sol: Here, equivalence relation ∼ on the set A is defined as:
a1∼a2 if f(a1) = f(a2)
where a1, a2 ∈ A
So, consider ai, bi, ci,.. ∈A and α, β, γ,... ∈ B and the mapping as:
a1 ↦ α, a2 ↦ α, a3 ↦ α,..., am ↦ α
Similarly,
b1 ↦ β, b2 ↦ β, b3 ↦ β,...,bn ↦ β
c1 ↦ γ, c2 ↦ γ, c3 ↦ γ,...,cp ↦ γ
and so on for the non-empty sets A and B and it is given that f : A → B is an onto function.
According to the definition of Equivalence relation, Equivalence class is:
[a1] = [a2] = [a3] =...= [am]
[b1] = [b2] = [b3] =...= [bn]
[c1] = [c2] = [c3] =...= [cp]
and so on.
Now, set of equivalence classes under relation ∼ is defined as:
E = {[a1], [b1], [c1],...}
Now, given the new mapping F : E → B as:
F([x]) = f(x) for all [x] ∈ E
It means mapping would be:
a1 ↦ α
b1 ↦ β
c1 ↦ γ
and so on.
Since, all distinct a1, b1, c1,... maps to different elements of set B and so, F is an injective function. Here, we have taken a1, b1, c1,... as a leader for their own equivalence classes, you can take a2, b2, c2,... so on.
It is cleared from the mapping of F that all the elements of set B are covered,so, F is surjective function because each element from their own equivalence class maps to according to the mapping of f. We have taken one element from the group of a′s and maps to α and similarly for other groups of b′s, c′s and so on.
Since, F is both injective and surjective and hene F is bijective function.
Here, we say, function F well-defined or single-valued when:
1) F ⊆ [x] × f(x)
2) The domain of F is [x]
3) if ([x], y), ([x], z) then y = z
Since from the mapping of F, it is cleared all the above three conditions are true because we have taken one element from the group of a′s, b′s, c′s,... and maps to α, β, γ,... and so, f is well-defined function.
Therefore, (B), (C), (D).
Q4: Which one of the following is the closed form for the generating function of the sequence {an}n≥0 defined below? (2022)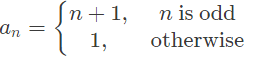 (a)
(a) 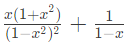 (b)
(b) 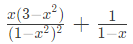 (c)
(c) 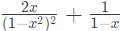 (d)
(d) 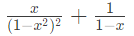 Ans: (a)
Ans: (a)
Sol: Corresponding Sequence would be –
a0, a1, a2, a3, a4,…∞
= 1, 2, 1, 4, 1, 6, 1, 8, 1, 10, 1 … ∞
= 1x0 + 2x1 + 1x2 + 4x3 + 1x4 + 6x5 + 1x6 + 8x7 + 1x8 + 10x9 + 1x10…
A = 1 + x2 + x4 + x6 + …∞
= 1/1 − x2
B = 2x1 + 4x3 + 6x5 + 8x7 + 10x9 + … ∞
It is sum of AP and GP. (Where 2, 4, 6, 8, 10 forms a AP and x1, x3, x5, x7, x9 forms a GP.)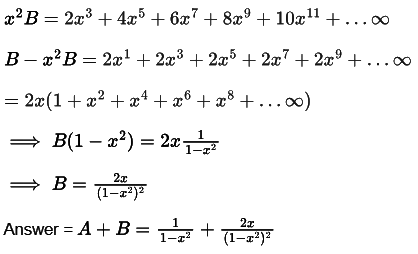 Since none of the the option is matching hence let’s simplify A.
Since none of the the option is matching hence let’s simplify A.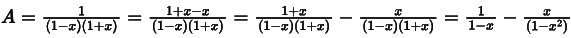 Now
Now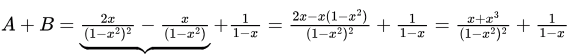 Hence A is answer.
Hence A is answer.
Q5: Consider the following sets, where n ≥ 2:
S1: Set of all nxn matrices with entries from the set {a, b, c}
S2: Set of all functions from the set{0, 1, 2 ,..., n2 − 1} to the set {0, 1, 2}
Which of the following choice(s) is/are correct?
[MSQ] (2021 SET-2)
(a) There does not exist a bijection from S1 to S2
(b) There exists a surjection from S1 to S2
(c) There exists a bijection from S1 to S2
(d) There does not exist an injection from S1 to S2
Ans: (b, c)
Sol: S1: There are n2 element in the matrix, we have 3 choices for each element, so number of such matrices = 
S2: There are n2 total elements with 3 choices for each element, so number of functions possible =
As the cardinality of both the sets are same, we can establish a bijection from one set to another. As bijection is possible, surjection is also possible.
So options B and C.
Q6: If the ordinary generating function of a sequence 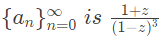 then a3−a0 is equal to ______. (2017 SET-2)
then a3−a0 is equal to ______. (2017 SET-2)
(a) 16
(b) 17
(c) 15
(d) 14
Ans: (c)
Sol: 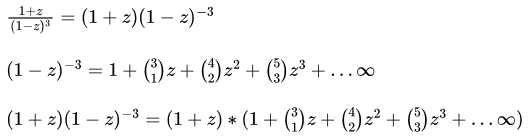 a0 is the first term in the expansion of above series and a3 is the fourth term (or) coefficient of z3
a0 is the first term in the expansion of above series and a3 is the fourth term (or) coefficient of z3
a0 = coefficient of z0 =1
a3 = coefficient of z3 = 
⇒ a3- a0 = 16 - 1 = 15
Q7: If g(x) = 1 − x and h(x) = x/(x−1), then 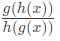 is: (2015 SET-1)
is: (2015 SET-1)
(a) h(x)/g(x)
(b) (-1)/x
(c) g(x)/h(x)
(d) x/(1-x)2
Ans: (a)
Sol: option (a) is correct. option (A)
option (A)
Q8: Let A be a finite set having x elements and let B be a finite set having y elements. What is the number of distinct functions mapping B into A. (2014)
(a) xy
(b) 2(x+y)
(c) yx
(d) y!/(y - x)!
Ans: (a)
Sol: Set A have x elements and B set have y elements. Each elements in B has x choices to be mapped to and being a function it must map to some element.Since each element has exactly x choices,
The total number of functions from B to A 
Hence, Option(A) xy is the correct choice.
For example we can consider A = {1} and B = {1, 2}. Now, only possible function from B → A is
1. {(1, 1), (2, 1)}
Q9: Consider the set of all functions f:{0, 1 ,..., 2014} → {0, 1 ..., 2014} such that f(f(i)) = i, for 0 ≤ i ≤ 2014 . Consider the following statements.
P. For each such function it must be the case that for every i, f(i) = i,
Q. For each such function it must be the case that for some i, f(i) = i,
R. Each such function must be onto.
Which one of the following is CORRECT? (2014 SET-3)
(a) P, Q and R are true
(b) Only Q and R are true
(c) Only P and Q are true
(d) Only R is true
Ans: (b)
Sol: Let f(i) = j. Now, we have f(j) = i, as per the given condition f(f(i)) = i.
For any i ≠ j, we can have a mapping f(i) = j, f(j) = i thus avoiding the condition f(i) = i. But since the domain set contains odd number of elements, at least for one element we must have f(i) = i. So, Q must be TRUE.
Since f(i) = j and f(j) = i, and since 0 ≤ i ≤ 2014 i must take all 2015 possible values (since f is a function, it must have a value for any element in the domain). We can easily see that f(i) cannot be the same for two different is- because suppose f(2) = 5, and f(3) = 5. Now as per given condition, f(5) = 2 and f(5) = 3, which is not allowed in a function. So, all f(i) values are unique ⇒ co-domain = range as there are only 2015 values in co-domain. So, R is true.
An identity function satisfies the given conditions. But that alone cant prove that P is true. We can also have a different function where all even numbers maps to the next odd number and all odd numbers map to the previous even number which satisfies the given conditions, except the last one as we have odd number in set. i.e.,
f(0) = 1, f(1) = 0, f(2) = 3, f(3) = 2…, f(2013) = 2012, f(2014) = 2014.
This proves, P is false.
So, (B) is the answer.
Q10: Let S denote the set of all functions f : {0, 1}4 → {0, 1}. Denote by N the number of functions from S to the set {0, 1}. The value of log2log2N is______. (2014 SET-1)
(a) 4
(b) 8
(c) 16
(d) 32
Ans: (c)
Sol: For a function from set A to set B, we need to have a mapping for all elements of A and mapping must be unique.
Let number of elements in A be m and that in B be n
So, if we consider an element from A, it can be mapped to any of the element from B. i.e., it has n possibilities when a function is formed. Similarly, for all other members also there are n possibilities as one element from A can be mapped to only a single element in B (though reverse need not true). So, for m elements in A, we totally have 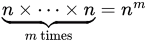 possible functions.
possible functions.
 as {0, 1}4 contains 24 elements. So, number of functions from S to {0, 1} will be
as {0, 1}4 contains 24 elements. So, number of functions from S to {0, 1} will be  . So, log2log2N = 24 = 16.
. So, log2log2N = 24 = 16.Q11: How many onto (or surjective) functions are there from an n-element (n ≥ 2 ) set to a 2-element set? (2012)
(a) 2n
(b) 2n−1
(c) 2n− 2
(d) 2(2n−2)
Ans: (c)
Sol: No. of onto (or surjective) functions are there from an n-element (n ≥ 2) set to a 2-element set = Total No of functions − (No of functions with 1 element from RHS not mapped) + (No of functions with 2 element from RHS not mapped)…(So on Using Inclusion Excusion principle =2n (Total no of functions ) − 2∗1n ( No of functions in which one element is excluded) +0 (No element in RHS is selected) = 2n−2.
Hence, Ans is (C).
|
34 videos|123 docs|72 tests
|
FAQs on Previous Year Questions: Functions - Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE)
| 1. What is a function in computer science? |  |
| 2. How do you define a function in programming languages? |  |
| 3. What is the difference between a function declaration and function definition? |  |
| 4. How do functions help in code reusability? |  |
| 5. Can a function call itself? What is this concept called? |  |
|
34 videos|123 docs|72 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|














