Previous Year Questions: Graph Theory | Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE) PDF Download
Q1: The chromatic number of a graph is the minimum number of colours used in a proper colouring of the graph. The chromatic number of the following graph is _______ (2024 SET-2) (a) 1
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
Sol: The given graph is bipartite, where alternating 4 vertices can be put in one part & remaining alternating 4 vertices in the second part.
A bipartite graph with at least 1 edges always has chromatic number 2.
Q2: Let AA be the adjacency matrix of a simple undirected graph G. Suppose A is its own inverse. Which one of the following statements is always TRUE? (2024 SET-2)
(a) G is a cycle
(b) G is a perfect matching
(c) G is a complete graph
(d) There is no such graph G
Ans: (b)
Sol: To solve this question, you don't have to remember any theorem related to graph theory.
Let's take an example so that the given proof can be understood easily.
Suppose, we have an adjacency matrix A for a simple undirected graph of 4 vertices as: The good thing about this matrix is that it is a symmetric matrix and all the row vectors are mutually perpendicular and the column vectors are also mutually perpendicular and for each row and column there is only one entry has 1 and remaining entries are 0s. The diagonal entries are zeros.
The good thing about this matrix is that it is a symmetric matrix and all the row vectors are mutually perpendicular and the column vectors are also mutually perpendicular and for each row and column there is only one entry has 1 and remaining entries are 0s. The diagonal entries are zeros.
If you multiply the same matrix with itself then you get an Identity matrix because 1st row vector is same as first column vector, 2nd row vector is same as 2nd column vector and so on and each row and column vector has only one entry of 1 and when we multiply the corresponding row and column vector and do the summation, we get the result as 1 at the same position.
So, A2 = I which implies A = A−1
So, it satisfies the given condition in the question. The corresponding graph for this adjacency matrix is: So, except B, all the other options are eliminated.
So, except B, all the other options are eliminated.
So, here for all the graphs with the permutation of these 4 rows/columns with the diagonal entries as 0 satify the given condition.
Now comes to the proof.
Since, every adjacency matrix is also a symmetric matrix and so A = AT = A−1 implies A2 = AAT = ATA = In.
So An×n is an orthogonal matrix because both the row and column spaces of this matrix form an orthonormal basis of  (each row and column should be mutually perpendicular).
(each row and column should be mutually perpendicular).
It simply means that  entry in A2 is the dot/inner product of ith row and ith column. For example, a11 in A2 is the dot product of first row and first column.
entry in A2 is the dot/inner product of ith row and ith column. For example, a11 in A2 is the dot product of first row and first column.
Here, graph is simple and so A is a matrix of 0s and 1s. Since the result of dot product is 1, it means there should be only one entry of 1 in each row and each column with the same position so that vTv =  for each row/column vector v of 0s and 1s in A. It simply means if kth entry of 1st row is 1 then the kth entry should also be 1 in the 1st column.
for each row/column vector v of 0s and 1s in A. It simply means if kth entry of 1st row is 1 then the kth entry should also be 1 in the 1st column.
So, here, we can say that if vi is connected to vj then vj should also be connected to vi and there should not be any other connection for both vi and vj. In this way we can form the set of independent edges that cover the whole graph and So, G will definitely have a perfect matching.
So, Answer is B.
Note: The above result is true when n=even because perfect matching does not exist when the number of vertices are odd and you can prove it by making det(A) = 0 but for symmetric orthogonal matrix det(A) = ±1 (proof is quite interesting)
One more way to prove the statement is using the fact that every (i, j)th entry of Ak is the number of vi, vj − walks of length k in G.
Q3: The number of edges present in the forest generated by the DFS traversal of an undirected graph G with 100 vertices is 40 . The number of connected components in G is ____ (2024 SET-1)
(a) 41
(b) 101
(c) 160
(d) 60
Ans: (d)
Sol: The number of connected components in G is same as number of connected components in the forest generated by DFS traversal.
A forest with 100 vertices and 0 edges has 100 components.
Adding 1 edge will reduce the number of components by 1, as an additional edge will connect 2 components. Remember the resulting graph has to be a forest, it cannot have any cycle, i.e. we can only add the edge between vertices that belong to different components.
Repeatedly adding 1 edge 40 times, results in reduction of number of components by 1, 40 times. That means we will end up with 100 - 40 = 60 connected components.
Answer - 60
Q4: The chromatic number of a graph is the minimum number of colours used in a proper colouring of the graph. Let G be any graph with n vertices and chromatic number k. Which of the following statements is/are always TRUE? (2024 SET-1)
(a) G contains a complete subgraph with k vertices
(b) G contains an independent set of size at least n/k
(c) G contains at least k(k−1)/2 edges
(d) G contains a vertex of degree at least k
Ans: (b, c)
Sol: First Option is false because chromatic number 'k' not necessarily means that graph contains a clique on 'k' vertices. For example, Chromatic Number of a Cycle Graph on odd vertices is 3 but it doesn't contain any complete subgraph on 3 vertices.
Second Option is True by virtue of Pigeon-Hole Principle. If there are 'k' color classes and n vertices, then one color class size is atleast n/k. Note that, a color class is nothing but an independent set.
Third option is True because minimum number of edges between k color classes is C(K, 2) or 'k choose 2'
Fourth option is False because take a cycle graph on odd vertices, chromatic number is 3 but degree is not 3 for any vertex. Similarly, for any complete graph, degree for every vertex is n-1 but chromatic number is n.
Q5: Let G be a directed graph and T a depth first search (DFS) spanning tree in G that is rooted at a vertex v. Suppose T is also a breadth first search (BFS) tree in G, rooted at v. Which of the following statements is/are TRUE for every such graph G and tree T? (2024 SET-1)
(a) There are no back-edges in G with respect to the tree T
(b) There are no cross-edges in G with respect to the tree T
(c) There are no forward-edges in G with respect to the tree T
(d) The only edges in G are the edges in T
Ans: (c)
Sol:  1. Back edge possible
1. Back edge possible
2. cross edge possible
3. all edge of G not in T
Forward edge cant be there else it wont give same BFS and DFS
Ans must be option C which always true.
Q6: Let GG be a simple, finite, undirected graph with vertex set {v1,...,vn}. Let Δ(G) denote the maximum degree of G and let N = {1, 2,...} denote the set of all possible colors. Color the vertices of G using the following greedy strategy: for i = 1,...,n
color(vi) ← min{j ∈ N: no neighbour of vi is colored j}
Which of the following statements is/are TRUE? (2023)
(a) This procedure results in a proper vertex coloring of G.
(b) The number of colors used is at most Δ(G)+1.
(c) The number of colors used is at most Δ(G).
(d) The number of colors used is equal to the chromatic number of G.
Ans: (a, b)
Sol: Understand the Greedy Algorithm for Proper Vertex Coloring of an undirected graph: The Greedy Algorithm for Coloring Vertices
Option D is False: Greedy Algorithm Doesn't always provide Optimal Coloring
Option B is True, Option C is False: Relation between Chromatic Number & Maximum Degree
Another Example to show that the Option D is False:
Q7: Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices? (2022)
MSQ
(a) The diagonal entries of A2 are the degrees of the vertices of the graph.
(b) If the graph is connected, then none of the entries of An−1 + In can be zero.
(c) If the sum of all the elements of A is at most 2(n-1), then the graph must be acyclic.
(d) If there is at least a 1 in each of A's rows and columns, then the graph must be connected.
Ans: (a)
Sol: Simple undirected Adjacency matrix representation of Simple undirected unweighted graph
A should have diagonal entries as 0 ( because no self loops allowed in simple graphs )
A should be Symmetric matrix
Option A :
A2 diagonal elements = (1.1 or 0.0) + (1.1 or 0.0) + ….. + (1.1 or 0.0) [ n times ]
let some specific node C, if C - A edge present , then 1.1 instead of 0.0 with respect to node A in above eqn therefore for each edge between C and Veertexx, thereshould be one 1 in the above eqn
Therefore A2 diagonal elements = degree of the vertices of the graph
Option B :
Counter example : U --- V ---- W
Option C :
If there are isolated vertices and even though cycle present, then there is a possibility of sum of all elements of A is atmost 2(n-1).
So given statement is wrong.
Option D :
If there are 2 components with each component have more than one vertex, then also atleast one entry of each row and column is non-zero.
So given statement is wrong.
Q8: The following simple undirected graph is referred to as the Peterson graph. Which of the following statements is/are TRUE? (2022)
Which of the following statements is/are TRUE? (2022)
MSQ
(a) The chromatic number of the graph is 3.
(b) The graph has a Hamiltonian path.
(c) The following graph is isomorphic to the Peterson graph. (d) The size of the largest independent set of the given graph is 3. (A subset of vertices of a graph form an independent set if no two vertices of the subset are adjacent.)
(d) The size of the largest independent set of the given graph is 3. (A subset of vertices of a graph form an independent set if no two vertices of the subset are adjacent.)
Ans: (a, b, c)
Sol: Given graph is Petersen graph. 3 colors are sufficient and necessary to color it. Hamiltonian path exists in Peterson graph but not Hamiltonian cycle.
Hamiltonian path exists in Peterson graph but not Hamiltonian cycle. It’s chromatic number is 3 but note that doesn’t mean largest independent vertex set size is 3.
It’s chromatic number is 3 but note that doesn’t mean largest independent vertex set size is 3.
It has largest independent vertex size = 4 (red colored vertices in first graph)
Graph present in Option C is isomorphic to Peterson graph ( Isomorphic : we need to see it in another perception)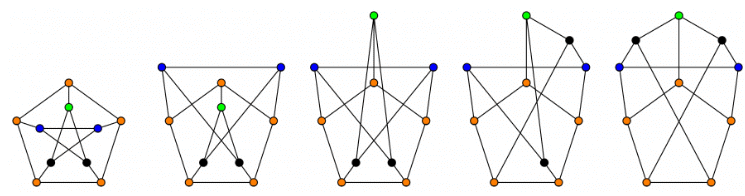
Q9: Consider a simple undirected unweighted graph with at least three vertices. If A is the adjacency matrix of the graph, then the number of 3-cycles in the graph is given by the trace of (2022)
(a) A3
(b) A3 divided by 2
(c) A3 divided by 3
(d) A3 divided by 6
Ans: (d)
Sol: Method 1 (How to solve instantly in Exam) :
Take a cycle graph on 3 vertices i.e. C3.
Write the adjacency matrix A of C3, find A3. The trace of A3 is 6, but we only have one 3-cycle(3 length cycle) in C3, So, we have to divide the trace of A3 by 6 to find out the number of 3-cycles. That’s our answer. Option D.
Method 2 (Complete Analysis) :
Definition of Walk : A walk consists of an alternating sequence of vertices and edges consecutive elements of which are incident, that begins and ends with a vertex.
In simple words, Walk from vertex w to v is sequence of “adjacent edges”, starting from w, ending at v, possibly with repetition of vertices or edges or both. Length of a walk is the number of edges on it.
For example, if we have cycle graph C3 whose vertices are P, Q, R, then, we have 2 walks of length 3 from P to P (P→Q→R→P;P→R→Q→P), similarly 2 walks of length 3 from R to R ; one walk of length 1 from P to R etc.
The Adjacency Matrix of a Graph :
The adjacency matrix M of a undirected graph is a matrix, by numbering the vertices, say from 1 up to n, and then putting Mij = Mji = 1 if there is an edge between i and j, and Mij = 0 otherwise.
We can do the same for a digraph: putting Mij = 1 if there is an edge from i to j, and Mij = 0 otherwise.
Powers of the Adjacency Matrix :
Let G be a graph (directed or undirected simple graph),  Let M be the adjacency matrix of G.
Let M be the adjacency matrix of G.
The powers of the adjacency matrix count things. In particular,
Entry i, j in Mn gives the number of walks from i to j of length n.
The proof is by induction argument. For example, the number of walks of length 2 from i to j is the number of vertices k such that there is an edge from i to k and an edge from k to j. And this is exactly the i, j entry in M2, by the definition of matrix multiplication.
Also, NOTE that for any graph G (directed or undirected simple graph), we can see that, every entry in adjacency matrix basically tells us that Number of walks of length 1 between the corresponding vertices of that entry, So, if Mij is 1, it means there is walk of length 1 from i to j, which is basically edge from i to j.
So, we have the following very Important Theorem :
If A is the adjacency matrix of a directed or undirected simple graph G, then the matrix An (i.e., the matrix product of n copies of A) has an interesting interpretation:
The element (i, j) gives the number of (directed or undirected) walks of length n from vertex i to vertex j.
Result :
The number of triangles in an undirected simple graph is exactly the trace of A3 divided by 6.
Why ??
Proof :
Note that in any simple undirected graph, we get a walk of length 3 from a vertex X to the same vertex X if and only if there is a triangle which contains X.
In any simple undirected graph, If you have a triangle T between vertices P, Q, R, then because of this particular triangle T, we have two walks of length 3 from P to P ; two walks of length 3 from Q to Q ; two walks of length 3 from R to R ; So, because of this one triangle T, in A3, we have contribution of 2 in entry (P, P) ; contribution of 2 in entry (Q, Q) ; contribution of 2 in entry (R, R) ; Hence, in the trace of A3, due to one triangle we have contribution of 6. So, the number of triangles in an undirected graph G is exactly the trace of A3 divided by 6.
For example, take a cycle graph on 3 vertices i.e. C3.
Write the adjacency matrix A of C3, find A3. The trace of A3 is 6, but we only have one 3-cycle in C3, So, we divide the trace of A3 by 6 to find out the number of 3-cycles.
Variation :
What happens if you have Simple Directed Graph ??
In any simple directed graph, If you have a directed triangle T between vertices P, Q, R, (P → Q → R → P), then because of this particular triangle T, we have one walk of length 3 from P to P ; one walk of length 3 from Q to Q ; one walk of length 3 from R to R ; So, because of this one triangle T, in A3, we have contribution of 1 in entry (P, P) ; contribution of 1 in entry (Q, Q) ; contribution of 1 in entry (R, R) ; Hence, in the trace of A3, due to one triangle we have contribution of 3. So, the number of triangles in an simple directed graph G is exactly the trace of A3 divided by 3.
For example, take a directed cycle graph on 3 vertices P, Q, R, i.e. (P → Q → R → P),.
Write the adjacency matrix M of this graph, find M3, the trace of M3 is 3, but we only have one 3-cycle in this graph, So, we divide the trace of M3 by 3 to find out the number of 3-cycles in simple directed graph.
Q10: Consider a simple undirected graph of 10 vertices. If the graph is disconnected, then the maximum number of edges it can have is . (2022)
(a) 72
(b) 36
(c) 16
(d) 48
Ans: (b)
Sol: We need a disconnected graph, that too with the maximum number of edges possible. To satisfy both these conditions, we can say that we must have a graph with exactly two components, each of which is a complete graph.
To maximize the number of edges, we should make a complete graph with 9 vertices, and isolate one vertex.
Hence, we get 36 edges. (In a complete graph on n vertices, we have nC2 edges. So, for a complete graph on 9 vertices, we have 9C2 = 36 Edges)
In general, we can say that, for n vertices disconnected graph, maximum number of edges possible is (n−1)C2.
Q11: In a directed acyclic graph with a source vertex s, the quality-score of a directed path is defined to be the product of the weights of the edges on the path. Further, for a vertex v other than s, the quality-score of v is defined to be the maximum among the quality-scores of all the paths from s to v. The quality-score of s is assumed to be 1. The sum of the quality-scores of all vertices on the graph shown above is ______ (2021 SET-2)
The sum of the quality-scores of all vertices on the graph shown above is ______ (2021 SET-2)
(a) 929
(b) 254
(c) 639
(d) 879
Ans: (a)
Sol: Let Q(v) denote the quality-score of vertex v. Therefore, the sum of the quality-scores of all vertices on the graph = 2 x 1 + 4 x 9 + 2 x 81 + 729 = 929.
Therefore, the sum of the quality-scores of all vertices on the graph = 2 x 1 + 4 x 9 + 2 x 81 + 729 = 929.
Q12: Consider the following directed graph: Which of the following is/are correct about the graph? (2021 SET-2)
Which of the following is/are correct about the graph? (2021 SET-2)
[MSQ]
(a) The graph does not have a topological order
(b) A depth-first traversal starting at vertex S classifies three directed edges as back edges
(c) The graph does not have a strongly connected component
(d) For each pair of vertices u and v, there is a directed path from u to v
Ans: (a, b)
Sol: Lets put numberings to the nodes as follows: The back edges are those edges from v to u in set (u,v) where u came first (i.e. already explored) in the DFS tree/forest.
The back edges are those edges from v to u in set (u,v) where u came first (i.e. already explored) in the DFS tree/forest.
- 3 to 2
- 12 to 11
- 9 to S
The DFS tree:
 The graph has two cycles one at bottom left and one at bottom right. And every cycle forms SCC (Strongly connected component, since from every vertex u, there is a path to v, u→v). C is false
The graph has two cycles one at bottom left and one at bottom right. And every cycle forms SCC (Strongly connected component, since from every vertex u, there is a path to v, u→v). C is false
The entire graph doesn’t have SCC. So, definitely D is false.
Due to the presence of cycles Topological Sort is not possible.
Hence, the answer is A and B.
D would have been correct if it was For some pair of vertices u and v there is a directed path from u to v.
Q13: An articulation point in a connected graph is a vertex such that removing the vertex and its incident edges disconnects the graph into two or more connected components.
Let T be a DFS tree obtained by doing DFS in a connected undirected graph G.
Which of the following options is/are correct? (2021 SET-1)
(a) Root of T can never be an articulation point in G.
(b) Root of T is an articulation point in G if and only if it has 2 or more children.
(c) A leaf of T can be an articulation point in G.
(d) If u is an articulation point in G such that x is an ancestor of u in T and y is a descendent of u in T, then all paths from x to y in G must pass through u.
Ans: (b)
Sol:  As per the option B it says root of T can be an articulation point in G if and only if it has 2 or more children, now here for simplicity I have taken simple case where root will have 2 children and I will tell you for the generalized case later. Also as its double implication lets see it as separately
As per the option B it says root of T can be an articulation point in G if and only if it has 2 or more children, now here for simplicity I have taken simple case where root will have 2 children and I will tell you for the generalized case later. Also as its double implication lets see it as separately
Case 1: If root is articulation point then root will have 2 or more children
If a vertex is articulation point then its removal disconnects the graph into 2 or more components means there must exist at least 2 vertices for which each and every path in between them will pass through articulation point and removal of articulation point will destroy all the paths in between them and thereby disconnecting the graph into components, otherwise that vertex can not be an articulation point because even if we remove that vertex still every pair of vertices has some other path and hence graph wont get disconnected.
Now when we start DFS Traversal from vertex V (articulation point) we may visit either the vertex from G1 or G2 first, lets say we visited vertex of G2 first now during the DFS traversal which becomes child of V now we can never visit any vertex in G1 unless and until we do not use vertex V because every path will go through vertex V only, and by the nature of DFS no vertex during the traversal of sub-graph G2 can visit the vertex V again as it will be having Gray color/ not yet finished (refer DFS algorithm from CLRS for better understanding) and because of this property all the vertices in G2 will be exhausted and we will be back to the vertex V but vertex V still has path to the unvisited vertices of sub-graph G1 and hence the first vertex which will be visited in G1 will become the new child of V thereby making 2 children for the root vertex V which is the articulation point.
Case 2: If root vertex has 2 or more children then it is articulation point
Lets say in an undirected graph if root has 2 children then it is true that there is no path between the vertices in left sub-tree and right sub-tree of vertex V (w.r.t DFS traversal tree) because if there had been any path between the left and right sub-tree the in that case if we start with right child then before reaching to the root all the vertices in left sub-tree would have been visited and root had only single child but it is contradiction as root has 2 children and hence there can be no path between the left and right sub-tree of vertex V, thereby making it the ONLY vertex through which vertices in left and right sub-tree are connected
Hence above two cases proves the option B is correct and A is incorrect
For the generalized case visualize star graph with many vertices where center is articulation point, now you got the intuition and apply this on any graph!
Lets understand option C.
Option C says that leaf of tree T can be an articulation point, its FALSE because if some vertex is leaf of tree T then all the vertices to which it connects are already been visited which indicates that even without using this leaf vertex there exists path between all of its neighbors and hence it can not be an articulation point.
Hence option C is incorrect
Now option D
Option D talks about ancestors and decedents X and Y and says that if X is ancestor of U in T and Y is decedent then all the paths between X and Y must pass through U but we have counter for this as shown below. Hence option D is incorrect.
Hence option D is incorrect.
Q14: G is an undirected graph with vertex set {v1, v2, v3, v4, v5, v6, v7} and edge set {v1v2, v1v3, v1v4 ,v2v4, v2v5, v3v4, v4v5, v4v6, v5v6, v6v7 }. A breadth first search of the graph is performed with v1 as the root node. Which of the following is a tree edge? (2020)
(a) v2v4
(b) v1v4
(c) v4v5
(d) v3v4
Ans: (b)
Q15: Graph G is obtained by adding vertex s to K3,4 and making s adjacent to every vertex of K3,4. The minimum number of colours required to edge-colour G is _______ (2020)
(a) 4
(b) 5
(c) 6
(d) 7
Ans: (d)
Sol: Easiest & Correct way to solve it:
First understand the given graph G:
It has maximum degree Δ = 7, degree sequence 7, 5, 5, 5, 4, 4, 4, 4 (Vertex s has degree 7, three vertices have degree 5 and remaining four vertices have degree 4)
Now, Some Important Theorems about Edge Coloring:
1. In the Edge Coloring of a graph G: The least number of colors needed to color the edges of G so that any two edges that share a vertex have different colors, is called Chromatic Index of G and it is denoted by χ′(G).
2. For any simple graph, χ′ ≥ Δ
For the given graph, Δ = 7, So, χ′ ≥ 7.
3. Vizing’s Theorem: For any simple graph, χ′ = Δ OR Δ + 1.
For the given graph, Δ = 7, So, χ′ = 7 OR 8.
Note that Graphs with χ′ = Δ are called Class-1 graphs, and Graphs with χ′ = Δ + 1 are called Class-2 graphs.
4. MOST Interesting & Useful Result by Vizing:
Vizing proved that Every graph with a unique vertex of maximum degree must be Class-1. More specifically, he showed that every class two graph must have at least three vertices of maximum degree.
So, if a graph G has ≤2 vertices of degree Δ, then G is Class-1 graph, Hence, χ′(G) = Δ.
For the given graph, there is Unique vertex of maximum degree Δ = 7, So, given graph is Class-1, Hence, χ′(G) = 7.
Q16: Let G be an undirected complete graph on n vertices, where n > 2. Then, the number of different Hamiltonian cycles in G is equal to (2019)
(a) n!
(b) (n-1)!
(c) 1
(d) 
Ans: (d)
Sol: The number of different Hamiltonian cycles in a complete undirected labeled graph on n vertices is (n−1)!/2.
If the graph is unlabeled number of different Hamiltonian cycles become 1.
Since the question does not mention whether the graph is labeled or not, answer can be either (C) or (D).
Official answer key is (D) or (C).
Q17: The number of edges in a regular graph of degree: d and n vertices is: (2018)
(a) maximum of n and d
(b) n+d
(c) nd
(d) nd/2
Ans: (d)
Sol: as every vertex has degree d,so sum of degrees is n*d.
we know 2* number of edges = sum of degrees
so, 2*E = nd
⇒ E = nd/2.
Q18: Which of the following is application of Breath First Search on the graph? (2018)
(a) Finding diameter of the graph
(b) Finding bipartite graph
(c) Both (A) and (B)
(d) None of the above
Ans: (c)
Sol: Some of the important applications of BFS are:
- Finding diameter of the graph.
- Finding the bipartite graph.
- Peer to peer networks.
- Shortest Path and Minimum Spanning Tree for the unweighted graph.
- Social Networking Websites.
- Crawlers in Search Engines.
- GPS Navigation Systems.
- Broadcasting in Network.
- In Garbage Collection.
- Cycle detection in the undirected graph.
- Ford Fulkerson algorithm.
- Path finding.
- Finding all nodes within a connected component.
Q19: Let G be a graph with 100! vertices, with each vertex labelled by a distinct permutation of the numbers 1,2,...,100. There is an edge between vertices u and v if and only if the label of u can be obtained by swapping two adjacent numbers in the label of v. Let y denote the degree of a vertex in G, and z denote the number of connected components in G. Then, y+ 10z = _____. (2018)
(a) 83
(b) 45
(c) 201
(d) 109
Ans: (d)
Sol: We have to find 2 things here, the degree of every vertex(which will be same for all vertices) and number of connected components.
Instead of 100, let's solve this by taking lesser value, say 4.
With 4! vertices, each vertex is a permutation of {1, 2, 3, 4}. So, we have vertices like {1, 2, 3, 4}, {1, 3, 2, 4}, {4, 1, 3, 2},… etc.
Here {1, 2, 3, 4} will be connected with
{2, 1, 3, 4}
{1, 3, 2, 4}
{1, 2, 4, 3}
To get this list, just take 2 adjacent numbers and swap them. eg. {1, 2, 3, 4} swap 1 and 2 to get {2, 1, 3, 4}.
The given 3 are the only permutations we can get by swapping only 2 adjacent numbers from {1, 2, 3, 4}. So, the degree of vertex {1, 2, 3, 4} will be 3. Similarly for any vertex it's degree will be 3.
Here we got ‘‘3" because we can chose any 3 pairs of adjacent numbers. So, with n, we have n−1 adjacent pairs to swap. So, degree will be n−1.
In our question, degree will be 100 − 1 = 99
Now let's see how many connected components we have.
It will be 1. Why?
If one can reach from one vertex to any other vertex, then that means that the graph is connected.
Now if we start with a vertex say {1, 2, 3, 4} we can reach to other vertex, say {4, 3, 2, 1} by the following path:
{1234}→{1243}→{1423}→{4123}→{4132}→{4312}→{4321}
Just take two adjacent numbers and swap them. With this operation you can create any permutation, from any given initial permutation.
This way you can show that from any given vertex we can reach any other vertex. This shows that the graph is connected and the number of connected components is 1.
y = 99 and z = 1
∴ y + 10z = 99 + 10 ∗ 1 = 109.
Q20: Let G be a simple undirected graph. Let TD be a depth first search tree of G. Let TB be a breadth first search tree of G. Consider the following statements.
(I) No edge of G is a cross edge with respect to TD. (A cross edge in G is between two nodes neither of which is an ancestor of the other in TD.)
(II) For every edge (u,v) of G, if u is at depth i and v is at depth j in TB, then |i - j| = 1.
Which of the statements above must necessarily be true? (2018)
(a) I only
(b) II only
(c) Both I and II
(d) Neither I nor II
Ans: (a)
Sol:
- Undirected graph cant have cross edges in DFS forest. (Only directed graphs can have) ( Hence I is True)
(If you do not agree just try it with taking examples. You cant draw) - Just draw a triangle SAB. Source is S. Vertex A and B are at same level hence distance 1. So here |i − j| = 0. (Hence II is false)
Hence answer is (A).
Anyway, II is simple to understand from the above explanation.
Those who did not get I, you may see Theorem 22.10 in Cormen)
Q21: The chromatic number of the following graph is _______. (2018) (a) 1
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c)
Sol: Here, Independent sets, S1 = {a, d}, S2 = {b, e}, S3 = {c, f}
Therefore, vertices of S1 has no connection between each other [∵ a & d are not connected by an edge]
S1 ⇒ put RED Vertices of S2 has no connection between each other [∵ b & e are not connected by an edge]
Vertices of S2 has no connection between each other [∵ b & e are not connected by an edge]
S2 ⇒ put GREEN Vertices of S3 has no connection between each other [∵ c & f are not connected by an edge]
Vertices of S3 has no connection between each other [∵ c & f are not connected by an edge]
S3 ⇒ put BLUE ∴ These graph has chromatic number as 3.
∴ These graph has chromatic number as 3.
Explanation: Why solving by independent sets?
Independent set means a set containing vertices & each & every vertex of this set is independent to each other i.e. if there are 3 vertices in an independent set, then each vertex of this set does not connected to other vertex of this set by an edge.
Suppose, there are two independent sets (S1 & S2). Then any vertex of S1 has connection(share an edge) to any vertex of set S2.
∵ S1, S2, S3 are different independent sets & they share some connection between them, we put different colours to different sets.
S1 share connections to S2 & S3
∴ Put RED to S1, not S2 & S3
Similarly, S2 share connections to S1 & S3
∴ Put GREEN to S2, not S1 & S3
S3 share connections to S1 & S2
∴ Put BLUE to S3, not S1 & S2
The advantage of following this method is when we have a complicated graph then we do not need to continuously see whether any vertex is adjacent to each other when we colour any vertex.
Q22: G is undirected graph with n vertices and 25 edges such that each vertex of G has degree at least 3. Then the maximum possible value of n is ____. (2017 SET-2)
(a) 15
(b) 16
(c) 17
(d) 18
Ans: (b)
Sol: Let m be minimum degree and M be maximum degree of a graph, then m ≤ (2E/V) ≤ M
m = 3, E = 25, V =...?
So, 
V ≤ (50/3)
V ≤ 16.667 ⇒ V = 16.
Q23: The Breadth First Search (BFS) algorithm has been implemented using the queue data structure. Which one of the following is a possible order of visiting the nodes in the graph below? (2017 SET-2) (a) MNOPQR
(a) MNOPQR
(b) NQMPOR
(c) QMNROP
(d) POQNMR
Ans: (d)
Sol: In BFS, starting from a node, we traverse all node adjacent to it at first then repeat same for next nodes.
Here, we can see that only option (D) is following BFS sequence properly.
- As per BFS, if we start from M then RQN (immediate neighbors of M) have to come after it in any order but in A here, O comes in between. So, it is not BFS.
- As per BFS, if we start from N then QMO has to come after it in any order but in B here, P comes. So, it is not BFS.
- As per BFS, if we start from Q then MNOP has to come after it in any order but in C here, R comes. So, it is not BFS.
But D is following the sequences.
So, D is the correct answer.
Q24: Let T be a tree with 10 vertices. The sum of the degrees of all the vertices in T is _________. (2017 SET-1)
(a) 20
(b) 18
(c) 10
(d) 19
Ans: (b)
Sol: Tree with n vertices which means n−1 edges.
n = 10 ∴ edges = n − 1 = 9.
∴ Sum of degree of all vertices ≤ 2E ≤ 2 ∗ 9 ≤ 18
Answer is 18.
Q25: The maximum number of edges in a n-node undirected graph without self loops is (2016)
(a) n2
(b) 
(c) n - 1
(d) 
Ans: (b)
Sol: In a graph of n vertices you can draw an edge from a vertex to (n−1) vertex we will do it for n vertices so total number of edges is n(n−1) now each edge is counted twice so the required maximum number of edges is 
Correct Answer: B.
Q26: A given connected graph G is a Euler Graph if and only if all vertices of G are of (2016)
(a) same degree
(b) even degree
(c) odd degree
(d) different degree
Ans: (b)
Sol: A given connected graph G is a Euler Graph if and only if all vertices of G are of even degree.
So option B is correct.
Q27: Breadth First Search(BFS) is started on a binary tree beginning from the root vertex. There is a vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the maximum possible value of n is______ . (2016 SET-2)
(a) 16
(b) 15
(c) 31
(d) 32
Ans: (c)
Sol: No of nodes at level 0 (root) of tree ⇒ 1
No of nodes at level 1 of tree ⇒ 2
No of nodes at level 2 of tree ⇒ 4
No of nodes at level 3 of tree ⇒ 8
No of nodes at level 4 of tree ⇒ 16
Last node in level 4th is the node we are looking for ⇒ 1 + 2 + 4 + 8 + 16 ⇒ 31
Q28: The minimum number of colours that is sufficient to vertex-colour any planar graph is _________. (2016 SET-2)
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (c)
Sol: Four color theorem is a famous result and it says that any planar graphs can be colored with only 4 colors.
Here ANY is used in sense of FOR ALL x. i.e., ANY means literally any one of graph can be selected !
Any man alive is gonna die ⇒ All men are gonna die and not any specific one.
Hope this clears thing a bit !
Q29: Consider the following directed graph: The number of different topological orderings of the vertices of the graph is (2016 SET-1)
The number of different topological orderings of the vertices of the graph is (2016 SET-1)
(a) 4
(b) 5
(c) 6
(d) 7
Ans: (c)
Sol: Here, start with a and end with f.
a _______ f
Blank spaces are to be filled with b, c, d, e such that b comes before c, and d comes before e. Number of ways to arrange b, c, d, e such that b comes before c and d comes before e, will be = 4!/(2!*2!) = 6
Q30: In a connected graph, a bridge is an edge whose removal disconnects a graph. Which one of the following statements is true? (2015 SET-2)
(a) A tree has no bridges
(b) A bridge cannot be part of a simple cycle
(c) Every edge of a clique with size ≥ 3 is a bridge (A clique is any complete subgraph of a graph)
(d) A graph with bridges cannot have a cycle
Ans: (b)
Sol: Bridge / cut edge : A single edge whose removal will disconnect the graph is known as Bridge or cut edge.
- Every edge of a tree is a bridge.
- A bridge cannot be a part of a single cycle because in a cycle every vertex will be connected with every other vertex in 2 ways. Even if you remove 1 way by deleting an edge still the other way will make sure that the graph is connected.
- A Clique will never have a bridge because though we remove 1 edge between any 2 vertices those 2 vertices will still be connected with the remaining (n−2) vertices using an edge each.
- Red edge in the below graph is clearly a bridge as removing that will produce an isolated vertex.

Q31: A graph is self-complementary if it is isomorphic to its complement. For all self-complementary graphs on n vertices, n is (2015 SET-2)
(a) A multiple of 4
(b) Even
(c) Odd
(d) Congruent to 0 mod 4, or, 1 mod 4
Ans: (d)
Sol:  where E(G) denotes the no. of edges in G. (G + G′ will be a complete graph)
where E(G) denotes the no. of edges in G. (G + G′ will be a complete graph)
for self complementary graphs, E(G) = E(G')
Q32: Let G = (V, E) be a simple undirected graph, and s be a particular vertex in it called the source. For x ∈ V, let d(x) denote the shortest distance in G from s to x. A breadth first search (BFS) is performed starting at s. Let T be the resultant BFS tree. If (u, v) is an edge of G that is not in T, then which one of the following CANNOT be the value of d(u) - d(v)? (2015 SET-1)
(a) -1
(b) 0
(c) 1
(d) 2
Ans: (d)
Sol: 2 is the answer.
d(u) − d(v) = 0 is possible when both u and v have an edge from from a common node t and t is in the shortest path from s to u and v.
d(u) − d(v) = 1 is possible when v and another node t are in the shortest path from s to u and both t and v are siblings- same distance from s to both t and v causing t − u edge to be in BFS tree and not v − u.
d(u) − d(v) = −1 is possible as explained above by interchanging u and v.
d(u) − d(v) = 2 is not possible. This is because on BFS traversal we either visit u first or v. Let's take u first. Now, we put all neighbors of u on queue. Since v is a neighbour and v is not visited before as assumed, d(v) will become d(u) + 1. Similarly, for v being visited first.
Q33: Let G be a connected planar graph with 10 vertices. If the number of edges on each face is three, then the number of edges in G is ____. (2015 SET-1)
(a) 30
(b) 24
(c) 27
(d) 18
Ans: (b)
Sol: By Euler formula for connected planar graph,
n − e + f = 2
10 − 3f/2 + f = 2 (An edge is part of two faces)
f/2 = 8
f = 16
e = 3f/2 = 24
Q34: A cube of side 1 unit is placed in such a way that the origin coincides with one of its top vertices and the three axes along three of its edges. What are the co-ordinates of the vertex which is diagonally opposite to the vertex whose co-ordinates are (1, 0, 1)? (2014)
(a) (0, 0, 0)
(b) (0, -1, 0)
(c) (0, 1, 0)
(d) (1, 1, 1)
Ans: (b)
Sol:  It should be B
It should be B
Draw the cube according to given information.
Q35: The conic section that is obtained when a right circular cone is cut through a plane that is parallel to the side of the cone is called _____ (2014)
(a) parabola
(b) hyperpola
(c) circle
(d) ellipse
Ans: (a)
Sol:  A circle cuts the axis at right angles.
A circle cuts the axis at right angles.
A ellipse cuts the axis at a angle less than 90.
A Parabola cuts parallel to the side of the cone . ( Answer A). )
A hyperbola cuts parallel to the axis.
Q36: If G is a forest with n vertices and k connected components, how many edges does G have? (2014 SET-3)
(a) ⌊n/k⌋
(b) ⌈n/k⌉
(c) n - k
(d) n - k +1
Ans: (c)
Sol: A forest is a collection of trees. here we are given a forest with n vertices and k components. a component is itself a tree.
Since there are k components means that every component has a root (every tree has one), therefore we have k roots.
Introduction of each new vertex to the forest introduces a single edge to a forest. so for remaining n − k vertices when introduced, to make up to n vertices, contributes to n − k edges.
Hence, ans = option (C) = (n - k).
Q37: Suppose depth first search is executed on the graph below starting at some unknown vertex. Assume that a recursive call to visit a vertex is made only after first checking that the vertex has not been visited earlier. Then the maximum possible recursion depth (including the initial call) is _________. (2014 SET-3) (a) 16
(a) 16
(b) 19
(c) 17
(d) 20
Ans: (b)
Sol: Total 21 nodes are there. 2 nodes require back track here in this question.
So, max recursion depth is 21 − 2 = 19
(Do DFS from extreme ends such that max recursion depth will occur. i.e., take leftmost top node as initial node for DFS as shown in below image) Note:- Backtrack means it reduces recursion depth in stack.
Note:- Backtrack means it reduces recursion depth in stack.
Q38: A cycle on n vertices is isomorphic to its complement. The value of n is _____. (2014 SET-2)
(a) 4
(b) 7
(c) 5
(d) 8
Ans: (c)
Sol: A cycle with n vertices has n edges.
Number of edges in cycle = n
Number of edges in its complement = 
Fo isomorphism, both graphs should have equal number of edges.
This gives: ⇒ n = 5.
⇒ n = 5.
Q39: The maximum number of edges in a bipartite graph on 12 vertices is _____. (2014 SET-2)
(a) 24
(b) 36
(c) 48
(d) 60
Ans: (b)
Sol: Maximum no. of edges occur in a complete bipartite graph i.e. when every vertex has an edge to every opposite vertex.
Number of edges in a complete bipartite graph is mn, where m and n are no. of vertices on each side. This quantity is maximum when m = n i.e. when there are 6 vertices on each side, so answer is 36.
Q40: An ordered n-tuple (d1, d2,...,dn) with d1 ≥ d2 ≥ ... ≥ dn is called graphic if there exists a simple undirected graph with n vertices having degrees d1, d2 ,..., dn respectively. Which of the following 6-tuples is NOT graphic? (2014 SET-1)
(a) (1, 1, 1, 1, 1, 1)
(b) (2, 2, 2, 2, 2, 2)
(c) (3, 3, 3, 1, 0, 0)
(d) (3, 2, 1, 1, 1, 0)
Ans: (c)
Sol: This can be solved using havel-hakimi theorem.
The idea is simple : Remove a vertex, which results into decrease of degree by 1 of each vertex which was connected to it. Keep removing like this, and if we get any negative degree, the degree sequence was not possible.
We need not check (A) and (B) as they are clearly graphs : (A) is 3 disconnected edges and (B) is 2 disconnected triangles.
For (C), we remove first vertex of degree 3, and thus decrease degree by 1 of next 3 vertices, so we get (2, 2, 0, 0, 0), then we remove vertex of degree 2, and decrease degree of next 2 vertices to get (1, −1, 0, 0). Since we get negative degree, original degree sequence is impossible.
For (D) : (3, 2, 1, 1, 1, 0) ⇒ (1, 0, 0, 1, 0). Now since this list is not sorted (which is required to apply further steps of algorithm), we sort it to get (1, 1, 0, 0, 0). Then we continue our algorithm on this list to get (0, 0, 0, 0), which is valid (4 isolated vertices).
So (C) is answer.
Q41: Consider an undirected graph G where self-loops are not allowed. The vertex set of G is {(i, f):1 ≤ i ≤ 12, 1 ≤ j ≤ 12}. There is an edge between (a, b) and (c, d) if |a - c| ≤ 1 and |b - d| ≤ 1. The number of edges in the graph is ____. (2014 SET-1)
(a) 1012
(b) 506
(c) 408
(d) 816
Ans: (b)
Sol: If you think of a 12 × 12 grid (like a chess board of size 12 × 12), then each each point (i, j), which is in ith row and jth column, is a vertex (i, j).
Now we are allowed to connect only those points which are atmost 1 distance apart (in both horizontal and vertical direction). So we will connect only horizontal neighbours, vertical neighbours, and diagonal neighbours.
So horizontal edges on each row are 11 i.e. 11 × 12 = 132 horizontal edges. Similarly we have 132 vertical edges.
To count diagonal edges, think of 1 × 1 square boxes in which diagonals meet each other. There are 11 × 11 such square boxes, and each box contains 2 diagonals, so total diagonals = 242.
So total edges = 132 + 132 + 242 = 50.
Q42: Consider the directed graph given below. Which one of the following is TRUE? (2014 SET-1)
Which one of the following is TRUE? (2014 SET-1)
(a) The graph does not have any topological ordering
(b) Both PQRS and SRQP are topological orderings
(c) Both PSRQ and SPRQ are topological orderings.
(d) PSRQ is the only topological ordering
Ans: (c)
Sol: C. Both PSRQ and SPRQ are topological orderings
- Apply DFS by choosing P or S as starting vertices
- As the vertex gets a finishing time assign it to the head of a linked list
- The linked list is your required topological ordering
Q43: Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time of Depth First Search on G, when G is represented as an adjacency matrix? (2014 SET-1)
(a) Θ(n)
(b) Θ(n+m)
(c) Θ(n2)
(d) Θ(m2)
Ans: (c)
Sol: Depth First Search of a graph takes O(m + n) time when the graph is represented using adjacency list. In adjacency matrix representation, graph is represented as an n ∗ n matrix. To do DFS, for every vertex, we traverse the row corresponding to that vertex to find all adjacent vertices (In adjacency list representation we traverse only the adjacent vertices of the vertex). Therefore time complexity becomes O(n2).
Correct Answer: C
Q44: Let G = (V, E) be a directed graph where V is the set of vertices and E the set of edges. Then which one of the following graphs has the same strongly connected components as G ? (2014 SET-1)
(a) G1 = (V, E1) where E1 ≡ {(u, v)∣(u, v) ∉ E}
(b) G2 = (V, E2) where E2 ≡ {(u, v)∣(v, u) ∈ E}
(c) G3 = (V, E3) where E3 ≡ {(u, v) there is a path of lenth ≤ 2 from u to v in E}
(d) G4 = (V4, E) where V4 is the set of vertices in G which are not isolated
Ans: (b)
Sol: (A) is false. Consider just two vertices connected to each other. So, we have one SCC. The new graph won't have any edges and so 2 SCC.
(B) is true. In a directed graph an SCC will have a path from each vertex to every other vertex. So, changing the direction of all the edges, won't change the SCC.
(D) is false. Consider any graph with isolated vertices- we loose those components.
(C) is a bit tricky. Any edge is a path of length 1. So, the new graph will have all the edges from old one. Also, we are adding new edges (u, v). So, does this modify any SCC? No, because we add an edge (u, v), only if there is already a path of length ≤2 from u to v- so we do not create a new path. So, both (B) and (C) must answer, though GATE key says only B.
Q45: The number of edges in a 'n' vertex complete graph is? (2013)
(a) n*(n−1)/2
(b) n2
(c) n*(n+1)/2
(d) n*(n+1)
Ans: (a)
Sol: Option a is right answer
In a complete graph each vertex is associated with all other vertes . They dont have self loop
So in Complete graph of n vertices each vertex has a degree of n - 1
Therfore n vertex will have n (n - 1) degree....1
And we know that sum of degree of vertex = 2 * edges
n*(n-1) = 2*e
e = n(n-1)/2.
Q46: How many diagonals can be drawn by joining the angular points of an octagon? (2013)
(a) 14
(b) 20
(c) 21
(d) 28
Ans: (b)
Sol: If we have a polynomial having n vertices then corresponding to each vertices we will have total (n-3) diagonals. ( By joining a vertex to every other vertices except its 2 neighbours. )
So total number of diagonal = n *(n-3)/2 ( Dividing by 2 because of duplicate diagonals ).
Here n = 8 for octagon,
No of diagonal = (8-3)*8/2 = 20.
Q47: What is the cyclomatic complexity of a module which has seventeen edges and thirteen nodes? (2013)
(a) 4
(b) 5
(c) 6
(d) 7
Ans: (c)
Sol: Cyclomatic complexity is used for testing purpose. It is calculated by using below formula E - N + 2
= 17 - 13 + 2
= 4 + 2
= 6
Option c.
Q48: The line graph L(G) of a simple graph G is defined as follows:
There is exactly one vertex v(e) in L(G) for each edge e in G.
For any two edges e and e' in G, L(G) has an edge between v(e) and v(e'), if and only if e and e' are incident with the same vertex in G.
Which of the following statements is/are TRUE? (2013)
(P) The line graph of a cycle is a cycle.
(Q) The line graph of a clique is a clique.
(R) The line graph of a planar graph is planar.
(S) The line graph of a tree is a tree.
(a) P only
(b) P and R only
(c) R only
(d) P, Q and S only
Ans: (a)
Sol: P) True. Because every edge in cycle graph will become a vertex in new graph L(G) and every vertex of cycle graph will become an edge in new graph.
R) False. We can give counter example. Let G has 5 vertices and 9 edges which is a planar graph. Assume degree of one vertex is 2 and of all others are 4. Now, L(G) has 9 vertices (because G has 9 edges ) and 25 edges. (See below). But for a graph to be planar |E| <= 3 |V| − 6.
For 9 vertices |E| ≤ 3 ∗ 9 − 6
⇒ |E| ≤ 27 − 6
⇒ |E| ≤ 21. But L(G) has 25 edges and so is not planar.
As (R) is False option (B), (C) are eliminated.
(S) False. By counter example. Try drawing a simple tree which has a Root node ,Root node has one child A, node A has two child B and C. Draw its Line graph acc. to given rules in question you will get a cycle graph of 3 vertices.
So (D) also not correct.
∴ option (A) is correct.
For a graph G with n vertices and m edges, the number of vertices of the line graph L(G) is m, and the number of edges of L(G) is half the sum of the squares of the degrees of the vertices in G, minus m.
Q49: Which of the following statements is/are TRUE for undirected graphs?
P: Number of odd degree vertices is even.
Q: Sum of degrees of all vertices is even. (2013)
(a) P only
(b) Q only
(c) Both P and Q
(d) Neither P nor Q
Ans: (c)
Sol: Both are correct
P: sum of odd degree + sum of even degree = 2 × no. of edges
sum of odd degree = 2 × no. of edges - sum of even degree
The right hand side must be even as the difference of 2 even numbers is always even.
Q: each edge is counted twice so sum of degree is always even
Q50: Consider an undirected random graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is the expected number of unordered cycles of length three? (2013)
(a) 1/8
(b) 1
(c) 7
(d) 8
Ans: (c)
Sol: A cycle of length 3 requires 3 vertices.
Number of ways in which we can choose 3 vertices from 8 = 8C3 = 56.
Probability that 3 vertices form a cycle = Probability of edge between vertices 1 and 2 × Probability of edge
between vertices 2 and 3 × Probability of edge between vertices 1 and 3 So, expected number of cycles of length 3 = 56 x (1/8) = 7.
So, expected number of cycles of length 3 = 56 x (1/8) = 7.
Q51: Let G be a complete undirected graph on 6 vertices. If vertices of G are labeled, then the number of distinct cycles of length 4 in G is equal to (2012)
(a) 15
(b) 45
(c) 90
(d) 360
Ans: (b)
Sol: From 6 vertices we can select 4 distinct vertices in 6C4 = 15 ways.
Now, with 4 vertices, we can form only 3 distinct cycles. [See below]
So, total no. of distinct cycles of length 4 = 15 × 3 = 45.
No. of cyclic permutations of n objects = (n−1)! and for n = 4, we get 3! = 6 ways. But number of distinct cycles in a graph is exactly half the number of cyclic permutations as there is no left/right ordering in a graph. For example a − b − c − d and a − d − c − b are different permutations but in a graph they form the same cycle.
Since, 45 was not in the choice, marks were given to all in GATE.
Q52: Which of the following graphs is isomorphic to (2012) (a)
(a) 
(b) 
(c) 
(d) 
Ans: (b)
Sol: For these type of questions find which are not isomorphic.
The graph in option (A) has a 3 length cycle whereas the original graph does not have a 3 length cycle
The graph in option (C) has vertex with degree 3 whereas the original graph does not have a vertex with degree 3
The graph in option (D) has a 4 length cycle whereas the original graph does not have a 4 length cycle
so option B must be correct.
Q53: How many edges are there in a forest with v vertices and k components? (2011)
(a) (v+1)-k
(b) (v+1)/2-k
(c) v-k
(d) v+k
Ans: (c)
Sol: Forest is nothing but disjoint union of trees.
So no of edges in 'k' components of 'v' vertices is nothing but 
where vi is the no. of vertices in the ith component.
Q54: If node A has three siblings and B is parent of A, what is the degree of A? (2011)
(a) 0
(b) 3
(c) 4
(d) 5
Ans: (a)
Sol:  Now coming to question if node A has three siblings and B is the parent of A. This is the only information given.
Now coming to question if node A has three siblings and B is the parent of A. This is the only information given.
It is not given whether node A is an internal node or leaf node and also total number of node in the graph is not given.
So given information is not sufficient to decide what should be the degree of node A.
So the degree of node A can be any of the above.
Q55: The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order. Which of the following sequences can not be the degree sequence of any graph? (2010)
I. 7, 6, 5, 4, 4, 3, 2, 1
II. 6, 6, 6, 6, 3, 3, 2, 2
III. 7, 6, 6, 4, 4, 3, 2, 2
IV. 8, 7, 7, 6, 4, 2, 1, 1
(a) I and II
(b) III and IV
(c) IV only
(d) II and IV
Ans: (d)
Sol: A degree sequence d1, d2, d3…dn of non negative integer is graphical if it is a degree sequence of a graph. We now introduce a powerful tool to determine whether a particular sequence is graphical due to Havel and Hakimi
Havel–Hakimi Theorem :
→ According to this theorem, Let D be the sequence d1, d2, d3 … dn with d1 ≥ d2 ≥ d3 ≥ … dn for n ≥ 2 and di ≥ 0.
→ If each di = 0 then D is graphical
→ Then D0 be the sequence obtained by:
→ Discarding d1, and
→ Subtracting 1 from each of the next d1 entries of D.
→ That is Degree sequence D0 would be : d2−1, d3−1,…, dd1+1−1,…,dn
→ Then, D is graphical if and only if D0 is graphical.
Now, we apply this theorem to given sequences:
- 7, 6, 5, 4, 4, 3, 2, 1 → 5, 4, 3, 3, 2, 1, 0 → 3, 2, 2, 1, 0, 0→1, 1, 0, 0, 0→0, 0, 0, 0 so it is graphical.
- 6, 6, 6, 6, 3, 3, 2, 2→5, 5, 5, 2, 2, 1, 2 ( arrange in descending order) →5, 5, 5, 2, 2, 2, 1 → 4, 4, 1, 1, 1, 1 → 3, 0, 0, 0, 1 we cannot continue to get all 0′s, so it is not graphical.
- 7, 6, 6, 4, 4, 3, 2, 2 → 5, 5, 3, 3, 2, 1, 1 → 4, 2, 2, 1, 1, 0 → 1, 1, 0, 0, 0 → 0, 0, 0, 0 so it is graphical.
- 8, 7, 7, 6, 4, 2, 1, 1, here degree of a vertex is 8 and total number of vertices are 8, which is impossible, hence it is not graphical.
Hence, only option (I) and (III) are graphic sequence and answer is option-(D)
Q56: Let G = (V, E) be a graph. Define  where id is the number of vertices of degree d in G. If S and T are two different trees with ξ(S) = ξ(T), then (2010)
where id is the number of vertices of degree d in G. If S and T are two different trees with ξ(S) = ξ(T), then (2010)
(a) |S|= 2|T|
(b) |S|=|T|-1
(c) |S|=|T|
(d) |S|=|T|+1
Ans: (c)
Sol: Sum of degrees in a graph = 2|E|, as each edge contributes two to the sum of degrees. So, when sum of degrees are same, number of edges must also be same.
Trees with equal no of edges has to have equal no of vertices as No of Edges = No of vertices −1, in a tree.
So, should be |S| = |T|
Correct Answer: C.
|
34 videos|115 docs|72 tests
|
FAQs on Previous Year Questions: Graph Theory - Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE)
| 1. What is a graph in graph theory? |  |
| 2. What are the different types of graphs in graph theory? |  |
| 3. What is a path in a graph? |  |
| 4. How is the degree of a vertex in a graph calculated? |  |
| 5. What is the importance of graph theory in computer science engineering? |  |
|
34 videos|115 docs|72 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
















