Q1: Let Zn be the group of integers {0, 1, 2,…, n−1} with addition modulo nn as the group operation. The number of elements in the group Z2 × Z3 × Z4 that are their own inverses is (2024 SET-2)
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (c)
Sol: Here, first understand the problem.
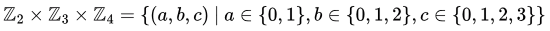 So,
So, 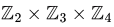 is a set of triplets in which first element comes from the set {0, 1} second element comes from the set {0, 1, 2} and third element comes from the set {0, 1, 2, 3}.
is a set of triplets in which first element comes from the set {0, 1} second element comes from the set {0, 1, 2} and third element comes from the set {0, 1, 2, 3}.
Q2: Consider the operators ⋄ and □ defined by a ⋄ b = a + 2b, a □ b = ab, for positive integers. Which of the following statements is/are TRUE? (2024 SET-1)
(a) Operator ⋄ obeys the associative law
(b) Operator □ obeys the associative law
(c) Operator ⋄ over the operator □ obeys the distributive law
(d) Operator □ over the operator ⋄ obeys the distributive law
Ans: (b, d)
Sol: Operation 1 : a ◊ b = a +2b
NOTE : An operation # is said to be associative if : (a # b) # c = a # (b # c).
Let's first try to observe option A and B.
Option A : Operation 1 follows Associativity?
(a ◊ b) ◊ c = (a+2b) ◊ c = a + 2b + 2c
a ◊ (b ◊ c) = a ◊ (b + 2c) = a + 2b + 4c
Here, (a ◊ b) ◊ c ≠ a ◊ (b ◊ c).
So, Option A is rejected.
Option B: Operation 2 follows Associativity?
(a ◻ b) ◻ c = (ab) ◻ c = abc.
a ◻ (b ◻ c) = a ◻ (bc) = abc
Here, (a ◻ b) ◻ c = a ◻ (b ◻ c).
So, Option B is Accepted.
NOTE : An operator % is distributive over @ if a % (b @ c) = (a % b) @ (a % c).
Option C: Operator ◊ is distributive over ◻?
Is a ◊ (b ◻ c) = (a ◊ b) ◻ (a ◊ c) ?
a ◊ (b ◻ c) = a ◊ (bc) = a + 2bc
(a ◊ b) ◻ (a ◊ c) = (a + 2b) ◻ (a+2c) = a2+2ac+2ab+4bc.
Here, a ◊ (b ◻ c) ≠ (a ◊ b) ◻ (a ◊ c).
So, Option C is rejected.
Option D: Operator ◻ is distributive over ◊?
Is a ◻ (b ◊ c) = (a ◻ b) ◊ (a ◻ c)?
a ◻ (b ◊ c) = a ◻ (b+2c) = ab + 2ac
(a ◻ b) ◊ (a ◻ c) = (ab) ◊ (ac) = ab + 2ac.
Here, a ◻ (b ◊ c) = (a ◻ b) ◊ (a ◻ c).
So, Option D is Accepted.
So, Option B and Option D are the Correct Answers.
Q3: Which of the following statements is/are TRUE for a group G? (2022)
MSQ
(a) If for all x, y ∈ G, (xy)2 = x2y2, then G is commutative.
(b) If for all x ∈ G, x2 = 1, then G is commutative. Here, 1 is the identity element of G.
(c) If the order of G is 2 , then G is commutative.
(d) If G is commutative, then a subgroup of G need not be commutative.
Ans: (a, b, c)
Sol: There are many equivalent definitions (if and only if statements) for Abelian Groups.In the GATE exam so far, 3-4 definitions have been asked, but some more variations can be created.
Alternative Definitions/Variations of Abelian Groups
In Abstract Algebra, “Abelian” word is used as a synonym of “commutative”. So, Commutative Group is same as Abelian Group. (Abelian groups are named after early 19th century mathematician Niels Henrik Abel.)
Option D :
“If group G is commutative, then a subgroup of G need not be commutative” : False.
Theorem : Every subgroup of an abelian group has to be abelian.
Proof :- Let G be an abelian group, and suppose that H ≤ G.
Now we have to check that, for any a, b ∈ H, Do we have ab = ba ??
Since we have : a, b ∈ H ⊆ G, So a,b are elements of G and since G is abelian, So, ab = ba.
Option C : “If the order of group G is 2, then G is commutative” :
True.There is only one abstract group of order 2 possible. Or we can say that ALL the groups of order 2 are isomorphic(similar) to each other.
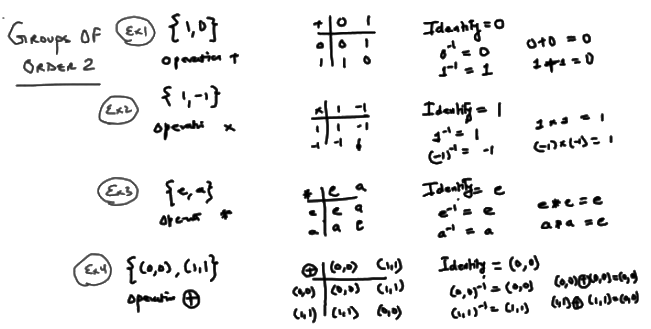 There is only one abstract group of order 2 possible and It can be easily seen that group of order 2 is abelian.
There is only one abstract group of order 2 possible and It can be easily seen that group of order 2 is abelian.
We can similarly see that every group of order less or equal to five is abelian.
Option B :“ If for all x ∈ G, x2 = 1, then G is commutative. Here, 1 is the identity element of G.” : True
Proof 1 :
Let a, b be two elements in group G. Consider the element ab.
Now, (ab)2 = 1
ab.ab = 1
Now, multiply both sides on the right with b,
aba = b
Now, multiply both sides on the right with a,
ab = ba
Hence, G is abelian. Proof 2 :
Let a,b be two elements in group G.
It is given that (ab)2 = 1 ; So, since (ab)(ab) = 1, So, ab is inverse of ab.
Now consider (ab)(ba).
(ab)(ba) = a(bb)a = aa = 1 ; So, (ab)(ba) = 1 ; which means that ba is inverse of ab.
But every element in a group has unique inverse, So, ab = ba.
Hence, G is abelian.
Option A :
” If for all x, y ∈ G, (xy)2 = x2y2 , then G is commutative ”. : True.
Since (ab)(ab) = (aa)(bb)
We know that in a group, left and right cancelation is allowed; So, Cancel left most ′a′ on both sides ; Cancel right most ′b′ on both sides;
We get ba = ab.
Q4: Let G be a group of order 6, and H be a subgroup of G such that 1 < |H| < 6. Which one of the following options is correct? (2021 SET-1)
(a) Both G and H are always cyclic.
(b) G may not be cyclic, but H is always cyclic.
(c) G is always cyclic, but H may not be cyclic.
(d) Both G and H may not be cyclic.
Ans: (b)
Sol: Given G is a group of order 6.
Lagrange's Theorem: The order of every subgroup of G divides the order of G
So, subgroup (H) of G can be the order of 1, 2, 3,and 6. But 6 is not possible as we need a proper sub-group, and 1 is not possible, as mentioned in the question.
Now, any group of prime order is cyclic. If the order is not-prime both cyclic and acyclic groups are possible.
Order of G = 6– Not a prime number so G may or may not be cyclic.
Order of H = {1, 2, 3} –2 and 3 are prime numbers and group with 1 element is cyclic. So, H is always cyclic.
Ans: (B) G may not be cyclic, but H is always cyclic.
Q5: Let G be a group of 35 elements. Then the largest possible size of a subgroup of G other than G itself is _______. (2020)
(a) 34
(b) 35
(c) 5
(d) 7
Ans: (d)
Sol: Lagrange's Theorem :
Order of subgroup must be factor of Order of group.
G is a group with 35 elements. So order of G = 35.
Factors of 35:1, 5, 7, 35
Proper subgroup: order of the subgroup is less than the order of group.
Order of the largest possible proper subgroup
Q6: (G,*) is an abelian group. Then (2018)
(a) x = x−1 for any x belonging to G
(b) x = x2 for any x belonging to G
(c) (x ∗ y)2 = x2∗y2, for any x,y belonging to G
(d) G is of finite order
Ans: (c)
Sol: (A) FALSE; if every element in the group is its own inverse, i.e x = x−1 for every x ϵ G ⇒ G is Abelian but the converse is not true.
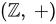 is an infinite abelian group but the following are not true for it:
is an infinite abelian group but the following are not true for it:
e = 0
x = x−1: Inverse of 1 ≠ 1 but = -1
(B) FALSE;
12 = 1 + 1 ≠ 1 but = 2
(C) TRUE; G is abelian if and only if (xy)2 = x2y2 for all x and y in G.
(⇒) Let x, y ∈ G. Then (xy)2 = xyxy = xxyx since G is abelian (COMMUTATIVE), and of course xxyy = x2y2. Thus (xy)2 = x2y2.
(⇐)
Assume (xy)2 = x2y2 for all x, y ∈ G. Then we have the following:(xy)2=x2y2xyxy=xxyyx−1xyxy=x−1xxyyyxy=xyyyxyy−1=xyyy−1yx=xyThus G is abelian.D) FALSE; Since (Z, +) is an infinite abelian group.
Q7: Let G be a finite group on 84 elements. The size of a largest possible proper subgroup of G is ________. (2018)
(a) 42
(b) 21
(c) 24
(d) 84
Ans: (a)
Sol: Order of a Subgroup always divides the order of Group.
Proper Subgroup of Group having order 84 would have one of the order (proper factors of 84) 2, 3, 4, 6, 7, 12, 14, 21, 28, 42.
So the largest order would be 42.
Q8: f(G,.) is a group such that (ab)−1 = a−1b−1, ∀a, b ∈ G, then G is a/an (2016)
(a) Commutative semi group
(b) Abelian group
(c) Non-abelian group
(d) None of these
Ans: (b)
Sol: In a group (G , .) is said to be abelian if
(a*b) = (b*a) ∀a, b ∈ G
∴ (ab)-1 = (b-1a-1) .....(1)
Given, (ab)-1 = a-1b-1 ....(2)
from (1) and (2) we can write
a-1b-1 = b-1 a-1
we can also write it as
ab = ba
Hence, Option (B) Abelian Group is the correct choice.
Q9: There are two elements x,y in a group (G,*) such that every element in the group can be written as a product of some number of x's and y's in some order. It is known that
x * x = y * y = x * y *x * y = y* x * y *x = e
where e is the identity element. The maximum number of elements in such a group is _______. (2014 SET-3)
(a) 3
(b) 4
(c) 5
(d) 6
Ans: (b)
Sol: It is given that:
- x is its own inverse.
- y is its own inverse.
- x∗y is its own inverse.
- y∗x is its own inverse.
Now I will show you that x∗y and y∗x are essentially same.
x ∗ y = x ∗ e ∗ y = x ∗ (x ∗ y ∗ x ∗ y) ∗ y = (x ∗ x) ∗ y ∗ x ∗ (y ∗ y) = e ∗ y ∗ x ∗ e = y ∗ x
(Group is associative so I do not care about brackets)
This turns out to be abelian group. and x ∗ y is no different from y ∗ x
Up to this point I have 4 elements - x, y, e, x ∗ y. (G is abelian therefore x ∗ y is same as y ∗ x)
Now see if you can have a new element. It is given that every element is product of some numbers of x and y.
Lets try with x.
x ∗ ∘, what u would like to put next to x ?
If you put x then there is no use and you have to start over again because of x∗x=e now you have to start all over again.
Put y next to x : x ∗y (this element we already have, we want different element so try multiplying further.)
x ∗ y ∗ ∘, obviously you cannot put y, next to x∗y because it will be x again: x ∗ y ∗ y = x ∗ e = x
(you have to put alternate.)
Put x, next to x ∗ y: x ∗ y ∗ x.
This is equal to x ∗ x ∗ y because of commutative property. x ∗ y ∗ x = x ∗ x ∗ y = y.
I showed you that, once you get x∗y using x, you can not get next element by multiplying into x ∗ y further. Because of commutative property it will be again x or y.
Similarly, if we start with y, we have the same issue.
This concludes that we can not generate further element and only four element can be there at max.
{x, y, x ∗ y, e}.
There is a theorem for abelian group: If every element is its own inverse then Group G is abelian. I am not sure if proof of that theorem relates to this problem somewhere, You can check it out. :)
Q10: Let G be a group with 15 elements. Let L be a subgroup of G. It is known that L ≠ G and that the size of L is at least 4. The size of L is _______. (2014 SET-3)
(a) 4
(b) 5
(c) 6
(d) 7
Ans: (b)
Sol: Lagrange's theorem: For any finite group G, the order (number of elements) of every subgroup L of G divides the order of G.
G has 15 elements.
Factors of 15 are 1, 3, 5, and 15.
Since, the given size of L is at least 4 (1 and 3 eliminated) and not equal to G(15 eliminated), the only size left is 5.
Size of L is 5.
Q11: The arithmetic mean of attendance of 49 students of class A is 40% and that of 53 students of class B is 35%. Then the percentage of arithmetic mean of attendance of class A and B is (2011)
(a) 27.20%
(b) 50.25%
(c) 51.13%
(d) 37.40%
Ans: (d)
Sol: AM of attendance of 49 students of class A = 40%
AM of attendance of 53 students of class B = 35%
AM of attendance of class A and B = 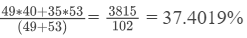
Hence,Option (D) 37.4% is the correct choice.
Q12: Consider the set S = {1, ω, ω2}, where ω and ω2 are cube roots of unity. If * denotes the multiplication operation, the structure (S, *) forms (2010)
(a) A group
(b) A ring
(c) An integral domain
(d) A field
Ans: (a)
Sol: 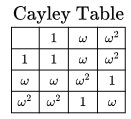 The structure (S, ∗) satisfies closure property, associativity and commutativity. The structure also has an identity element (=1) and an inverse for each element. So, the structure is an Abelian group.
The structure (S, ∗) satisfies closure property, associativity and commutativity. The structure also has an identity element (=1) and an inverse for each element. So, the structure is an Abelian group.
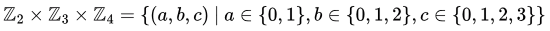 So,
So, 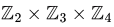 is a set of triplets in which first element comes from the set {0, 1} second element comes from the set {0, 1, 2} and third element comes from the set {0, 1, 2, 3}.
is a set of triplets in which first element comes from the set {0, 1} second element comes from the set {0, 1, 2} and third element comes from the set {0, 1, 2, 3}. 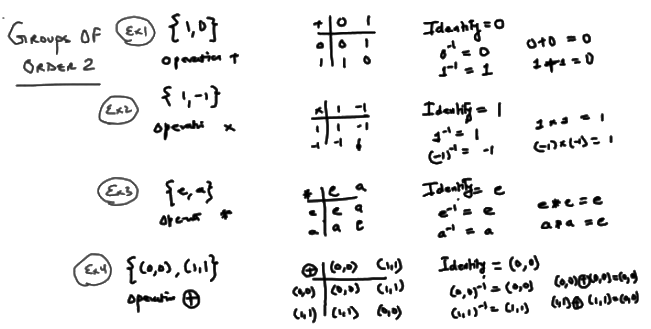 There is only one abstract group of order 2 possible and It can be easily seen that group of order 2 is abelian.
There is only one abstract group of order 2 possible and It can be easily seen that group of order 2 is abelian.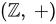 is an infinite abelian group but the following are not true for it:
is an infinite abelian group but the following are not true for it: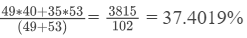
 The structure (S, ∗) satisfies closure property, associativity and commutativity. The structure also has an identity element (=1) and an inverse for each element. So, the structure is an Abelian group.
The structure (S, ∗) satisfies closure property, associativity and commutativity. The structure also has an identity element (=1) and an inverse for each element. So, the structure is an Abelian group. 




















