Previous Year Questions: Hashing | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Q1: An algorithm has to store several keys generated by an adversary in a hash table. The adversary is malicious who tries to maximize the number of collisions. Let k be the number of keys, m m be the number of slots in the hash table, and k > m k > m. (2023)
Which one of the following is the best hashing strategy to counteract the adversary?
(a) Division method, i.e., use the hash function h (k) = k mod m.
(b) Multiplication method, i.e., use the hash function h(k) = [m(kA − [kA])], where A is a carefully chosen constant.
(c) Universal hashing method.
(d) If k is a prime number, use Division method. Otherwise, use Multiplication method.
Ans: (c)
Sol: Universal hashing refers to selecting a hash function at random from a family of hash functions with a certain mathematical property. This guarantees a low number of collisions in expectation, even if the data is chosen by an adversary. It implements uniform hashing.
Q2: Suppose we are given n n keys, m m hash table slots, and two simple uniform hash functions h1 and h2. Further suppose our hashing scheme uses h1 for the odd keys and h2 for the even keys. What is the expected number of keys in a slot? (2022)
(a) m/n
(b) n/m
(c) 2n/m
(d) n/2m
Ans: (b)
Sol: Uniform hash function definition : Pr[h(x) = i] = 1/m
which means for every x, we have equal probability of mapping to any of slot i .
Quick Question-
Hash function give in question is Uniform
Take any slot i and calculate probability of mapping some arbitrary x to i ?
i.e. Pr[h(x) = i] = ?
Let the probability of choosing h1is p and choosing h2 is 1 − p then
Pr[h(x) = i] = p Pr [h1(x) = i] + (1 − p) Pr [h2(x) = i]
⇒ Pr [h(x) = i] = p/m + 1 − p/m (since h1and h2 both are uniform hash functions)
= 1/m
As you see, value of p does not matter but we can calculator p as = number of even keys /Total keys
Since h is uniform, we can say it will distribute all keys uniformly. This means if there are 50 keys and 10 slots then each slot will get 5
keys. i.e. n/m
But we can do this using probability.
let X = Number of items in slot 1. (Note that I am. only talking about some random slot, say slot 1)

Very easily, we can say X = X1 + X2 +… Xn
They are asking E[X]
E[X] = E[X1 + X2 + … X n]
E[X] = E[X1] + E[X2] + … E[X n]
How to calculate E[Xi] ?–There could be 2 methods, one given below and the other is in first comment.
Once we calculate P(Xi = 1) and P(Xi = 0) then finding E[Xi] is straight forward and so E[X]
P(Xi = 1) = 1/m because whatever happens within black box (h1 or h2), the overall hash function will be uniform.
E[Xi] = 1P (Xi = 1) + 0P(Xi = 0) = 1/m
Hence,
E[X] = n/m
Q3: Consider a dynamic hashing approach for 4-bit integer keys: (2021 SET 1)
1. There is a main hash table of size 4.
2. The 2 least significant bits of a key is used to index into the main hash table.
3. Initially, the main hash table entries are empty.
4. Thereafter, when more keys are hashed into it, to resolve collisions, the set of all keys corresponding to a main hash table. entry is organized as a binary tree that grows on demand.
5. First, the 3rd least significant bit is used to divide the keys into left and right subtrees.
6. To resolve more collisions, each node of the binary tree is further sub-divided into left and right subtrees based on the 4th least significant bit.
7. A split is done only if it is needed, i.e., only when there is a collision.
Consider the following state of the hash table.
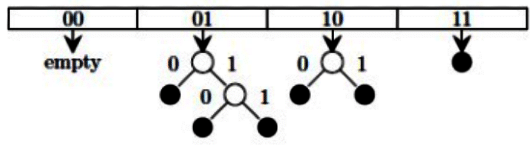 Which of the following sequences of key insertions can cause the above state of the hash table (assume the keys are in decimal notation)?
Which of the following sequences of key insertions can cause the above state of the hash table (assume the keys are in decimal notation)?
(a) 5,9,4,13,10,7
(b) 9,5,10,6,7,1
(c) 10,9,6,7,5,13
(d) 9,5,13,6,10,14
Ans: (c)
Sol:
- 1-0001
- 4-0100
- 5-0101
- 6-0110
- 7-011
- 9-1001
- 10-1010
- 13-1101
- 14-1110
A 5,9,4,13,10,7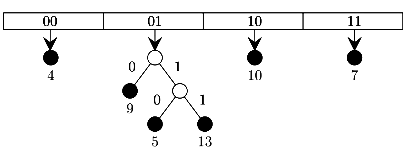 B 9,5,10,6,7,1
B 9,5,10,6,7,1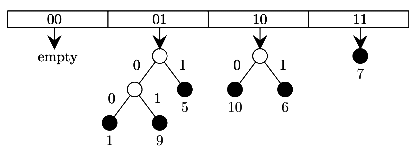 C 10,9,6,7,5,13
C 10,9,6,7,5,13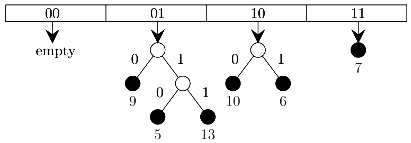 D 9,5,13,6,10,14
D 9,5,13,6,10,14
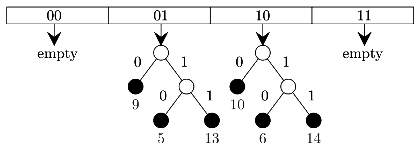 So only one option correct C.
So only one option correct C.
Q4: Consider a double hashing scheme in which the primary hash function is h1(k) = k mod 23 , and the secondary hash function is h2 (k) = 1 + (k mod 19). Assume that the table size is 23. Then the address returned by probe 1 in the probe sequence (assume that the probe sequence begins at probe 0) for key value k = 90 is_____________. (2020)
(a) 21
(b) 15
(c) 13
(d) 17
Ans: (c)
Sol: In double hashing scheme, the probe sequence is determined by (h1(k) + ih2(k)) mod m, where i denotes the index in probe sequence and m denotes the hash table size. Given h1(k) and h2(k), we have to determine the second element of the probe sequence (i.e. i = 1) for the key k = 90.
(h1(90) + 1 * h2(90)) mod 23 = (21 + 15) mod 23 = 36 mod 23 = 13
Q5: Given a hash table T with 25 slots that stores 2000 elements, the load factor α for T is ____________. (2015 SET 3)
(a) 2000
(b) 25
(c) 80
(d) 160
Ans: (c)
Sol: A critical statistic for a hash table is the load factor, that is the number of entries divided by the number of buckets:
Load factor = n/k
where:
n = number of entries
k = number of buckets
As the load factor grows larger, the hash table becomes slower, and it may even fail to work (depending on the method used).
Here, load factor = 2000/25 = 80
Q6: Which one of the following hash functions on integers will distribute keys most uniformly over 10 buckets numbered 0 to 9 for i ranging from 0 to 2020? (2015 SET 2)
(a) h(i) = i 2 mod 10
(b) h(i) = i3 mod 10
(c) h(i) = (11 * i2) mod 10
(d) h(i) = (12 * i2) mod 10
Ans: (b)
Sol: Since mod 10 is used, the last digit matters.
If we CUBE all numbers from 0 to 9, we get the following
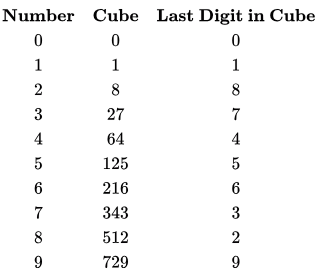 Therefore all numbers from 0 to 2020 are equally divided in to 10 buckets. If we make a table for square, we won't get equal distribution as shown in the following table. 1,4, 6 and 9 are repeated, so these buckets would have more entries and there are no buckets corresponding to 2 ,3 ,7 and 8
Therefore all numbers from 0 to 2020 are equally divided in to 10 buckets. If we make a table for square, we won't get equal distribution as shown in the following table. 1,4, 6 and 9 are repeated, so these buckets would have more entries and there are no buckets corresponding to 2 ,3 ,7 and 8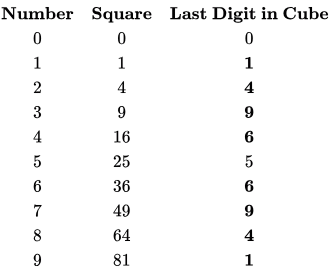
Correct Answer: B
Q7: Consider a hash table with 100 slots. Collisions are resolved using chaining. Assuming simple uniform hashing, what is the probability that the first 3 slots are unfilled after the first 3 insertions? (2014 SET 3)
(a) (97 x 97 x 97)/1003
(b) (99 x 98 x 97)/1003
(c) (97 x 96 x 95)/1003
(d) (97 x 96 x 95)/(3! x 1003)
Ans: (a)
Sol: We have 100 slots each of which are picked with equal probability by the hash function (since hashing is uniform). So, to avoid first 3 slots, the hash function has to pick from the remaining 97 slots. And repetition is allowed, since chaining is used- meaning a list of elements are stored in a slot and not a single element.
So, required probability = 97/100 × 97/100 × 97/100
= ( 97 × 97 × 97 ) / 1003
Q8: Consider a hash table with 9 slots. The hash function is h(k)=k mod 9. The collisions are resolved by chaining. The following 9 keys are inserted in the order: 5 , 28 , 19, 15, 20 , 33, 12, 17, 10. The maximum, minimum, and average chain lengths in the hash table, respectively, are (2014 SET 1)
(a) 3, 0, and 1
(b) 3, 3, and 3
(c) 4, 0, and 1
(d) 3, 0, and 2
Ans: (a)
Sol:
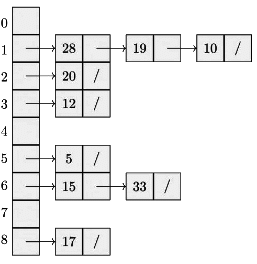
So, Maximum & minimum chain lengths are 3 & 0 respectively.
Average chain length = ( 0 + 3 + 1 + 1 + 0 + 1 + 2 + 0 + 1 ) / 9 = 1 .
So, Answer is A.
Q9: A hash table of length 10 uses open addressing with hash function h(k) = k mod 10, and linear probing. After inserting 6 values into an empty hash table, the table is as shown below (2010)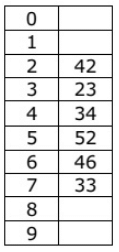 How many different insertion sequences of the key values using the same hash function and linear probing will result in the hash table shown above?
How many different insertion sequences of the key values using the same hash function and linear probing will result in the hash table shown above?
(a) 10
(b) 20
(c) 30
(d) 40
Ans: (c)
Sol: Slots 3 , 4 , 5 and 6 must be filled before 33 comes. Similarly slots 2,3 and 4 must be filled before 52 comes. And 52 must come before 33 , as it is not occupying slot 2 . So, 33 must be at the end and 52 can come at position 4 or 5 .
Let 52 come at position 4. Slots 2 ,3 and 4 must be filled before 52 leaving only slot 6 left for the element coming at position 5 which should be 46 . So, the first 3 elements can come in any order giving 3! = 6 ways.
Let 52 come at position 5. Now, the first four elements can come in any order. So, 4! = 24 ways.
So, total number of different insertion sequences possible = 24 + 6 = 30
Q10: A hash table of length 10 uses open addressing with hash function h(k)=k mod 10, and linear probing. After inserting 6 values into an empty hash table, the table is as shown below (2010)
 Which one of the following choices gives a possible order in which the key values could have been inserted in the table?
Which one of the following choices gives a possible order in which the key values could have been inserted in the table?
(a) 46, 42, 34, 52, 23, 33
(b) 34, 42, 23, 52, 33, 46
(c) 46, 34, 42, 23, 52, 33
(d) 42, 46, 33, 23, 34, 52
Ans: (c)
Sol: 46, 34, 42, 23, 52, 33
- 46−position 6
- 34 position 4
- 42 position 2
- 23 position 3
- 52 position 2 − collision next empty is 5
- 33 position 3 − collision next empty is 7
Q11: The keys 12, 18, 13, 2, 3, 23, 5 and 15 are inserted into an initially empty hash table of length 10 using open addressing with hash function h(k) = k mod 10 and linear probing. What is the resultant hash table? (2009)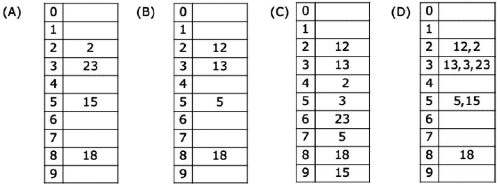
(a) A
(b) B
(c) C
(d) D
Ans: (c)
Sol: (C) is the correct option ..directly from the definition of linear probing. In linear probing, when a hashed location is already filled, locations are linearly probed until a free one is found.
Q12:Consider a hash table of size 11 that uses open addressing with linear probing. Let h(k)=kmod 11 be the hash function used. A sequence of records with keys
43 36 92 87 11 4 71 13 14
is inserted into an initially empty hash table, the bins of which are indexed from zero to ten. What is the index of the bin into which the last record is inserted? (2008)
(a) 3
(b) 4
(c) 6
(d) 7
Ans: (d)
Sol:
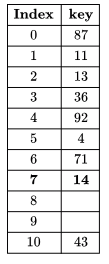 (D) is answer
(D) is answer
Q13: Consider a hash function that distributes keys uniformly. The hash table size is 20. After hashing of how many keys will the probability that any new key hashed collides with an existing one exceed 0.5. (2007)
(a) 5
(b) 6
(c) 7
(d) 10
Ans: (b)
Sol: After hashing of how many keys, will the probability that any new key hashed collides with an existing one exceed 0.5.
Here, 'new key hashed' is the ambiguity. It can mean the probability of a collision in the next 'hash', or the probability of a collision in any of the hashes of the 'new keys' starting from the first insertion. For the first case answer must be 10 to get probability equal to 0.5 , and so 11 must be the answer for probability > 0.5 . Thus we can conclude from given choices, it is the second case.
So, we need to find n such that after n hashes, probability of collision (in any of the n hashes) > 0.5 .
Probability that there will be a collision after n hashes (a collision happened in at least one of those n hashes) = 1 − Probability that there was no collision in the first n hashes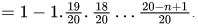 So, we need,
So, we need,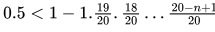
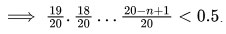 For n = 5 , we get, 0.5814 and for n = 6 , we get 0.43605 . So, answer should be n = 6 .
For n = 5 , we get, 0.5814 and for n = 6 , we get 0.43605 . So, answer should be n = 6 .
Correct Answer: B
Q14: Consider a hash table of size seven, with starting index zero, and a hash function (3x + 4) mod 7. Assuming the hash table is initially empty, which of the following is the contents of the table when the sequence 1, 3, 8, 10 is inserted into the table using closed hashing? Note that '-' denotes an empty location in the table. (2007)
(a) 8, -, -, -, -, -, 10
(b) 1, 8, 10, -, -, -, 3
(c) 1, -, -, -, -, -, 3
(d) 1, 10, 8, -, -, -, 3
Ans: (b)
Sol: The answer is (B). 1 will occupy location 0 ,3 will occupy location 6,8 hashed to location 0 which is already occupied so, it will be hashed to one location next to it. i.e. to location 1 .
Since 10 also clashes, so it will be hashed to location 2 .
Q15: A hash table contains 10 buckets and uses linear probing to resolve collisions. The key values are integers and the hash function used is key % 10. If the values 43, 165, 62, 123, 142 are inserted in the table, in what location would the key value 142 be inserted? (2005)
(a) 2
(b) 3
(c) 4
(d) 6
Ans: (d)
Sol: 43 in loc 3
165 in loc 5
62 in loc 2
123 in loc 4 ( collision and next free space)
142 in loc 6 (collision in 2 , and 3 , 4 , 5 already occupied)
hence answer D
Q16: Given the following input (4322, 1334, 1471, 9679, 1989, 6171, 6173, 4199) and the hash function x mod 10, which of the following statements are true? (2004)
i) 9679, 1989, 4199 hash to the same value
ii) 1471, 6171 has to the same value
iii) All elements hash to the same value
iv) Each element hashes to a different value
(a) i only
(b) ii only
(c) i and ii only
(d) iii or iv
Ans: (c)
Sol: Option C is correct answer because the last digit of every digit given is equal in I and II.
Q17: An advantage of chained hash table (external hashing) over the open addressing scheme is (1996)
(a) Worst case complexity of search operations is less
(b) Space used is less
(c) Deletion is easier
(d) None of the above
Ans: (c)
Sol:
A. False :- search operation can go worst in chaining if all elements are stored under a single bucket.
B. False . Pointer space is overhead in chaining.
C. is true BCZ in Open Addressing sometimes though element is present we cant delete it if Empty Bucket comes in between while searching for that element ;Such Limitation is not there in Chaining.
Q18: A hash table with ten buckets with one slot per bucket is shown in the following figure. The symbols S1 to S7 initially entered using a hashing function with linear probing. The maximum number of comparisons needed in searching an item that is not present is (1989)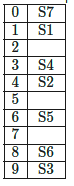 (a) 4
(a) 4
(b) 5
(c) 6
(d) 3
Ans: (b)
Sol: 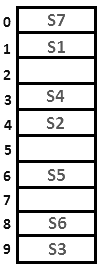
We can illustrate it as :
for position 8th when we calculate value of linear probing for First time we can't store value because it is already filled. So,
For 9th position we have to calculate value of probing for the Second time.
For 0th position we have to calculate value of probing for the Third time.
Similarly, for Ist position we have to calculate it for Fourth time but it is also filled previously.
so, for 2nd position when we calculate it for Fifth time place is empty here and value can be putted.
Maximum number of comparisons is that how many number of probes we have calculated for it.
So, number of probes here are 5 hence the answer.
|
159 docs|30 tests
|
FAQs on Previous Year Questions: Hashing - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is hashing in computer science? |  |
| 2. How does hashing help in improving data retrieval performance? |  |
| 3. What is a collision in hashing? |  |
| 4. Can hash functions guarantee unique hash codes for different keys? |  |
| 5. What are some common applications of hashing in computer science? |  |
















