Previous Year Questions: Heap Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Q1: Consider a binary min-heap containing 105 distinct elements. Let k be the index (in the underlying array) of the maximum element stored in the heap. The number of possible values of k is (2024 SET 1)
(a) 53
(b) 52
(c) 27
(d) 1
Ans: (a)
Sol: A binary heap is a complete binary tree.
A binary min-heap satisfies min-heap property. This implies that the maximum element can be in the leaves only.
No. of internal nodes in 105 element heap = [105/2] = 52
No. of leaves = 105-52=53.
Q2: An array [82,101,90,11,111,75,33,131,44,93] is heapified. Which one of the following options represents the first three elements in the heapified array? (2024 SET 1)
(a) 82,90,101
(b) 82,11,93
(c) 131,11,93
(d) 131,111,90
Ans: (d)
Sol: 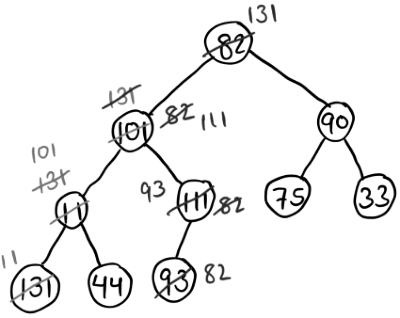
1. Heapify node with value 111. Nothing changes as max-heap property is already satisfied.
2. Heapify node with value 11. Now 11 is swapped with 131 so that max-heap property is satisfied. (blue colored text in image).
3. Heapify node with value 90. Nothing changes as max-heap property is already satisfied.
4. Heapify node with value 101. Now 101 is swapped with 131 so that max-heap property is satisfied. (red colored text in image)
5. Heapify node with value 82. Now 82 is swapped with 131, then 82 is swapped with 111, then 82 is swapped with 93 so that max-heap property is satisfied. (green colored text in image)
Final array -[131,111,90,101,93,75,33,11,48,82]
Q3: Let A be a priority queue for maintaining a set of elements. Suppose A is implemented using a max-heap data structure. The operation Extract-Max(A) extracts and deletes the maximum element from A. The operation Insert(A, key) inserts a new element key in A. The properties of a max-heap are preserved at the end of each of these operations.
When A contains n elements, which one of the following statements about the worst case running time of these two operations is TRUE? (2023)
(a) Both Extract-Max(A) and Insert(A, key) run in O(1).
(b) Both Extract-Max(A) and Insert(A, key) run in O(log(n)).
(c) Extract-Max(A) runs in O(1) whereas Insert(A, key) runs in O(n).
(d) Extract-Max(A) runs in O(1) whereas Insert(A ,key) runs in O(log(n))
Ans: (b)
Sol: Priority Queue containing n elements is implemented using Max-Heap.
We are also provided with 2 operations : EXTRACT-MAX(A) & INSERT(A,key).
EXTRACT-MAX(A) extracts maximum element and delete it.
Whereas, INSERT(A, key) inserts an element key in A.
Lets, start with considering INSERT(A, key) : If any key is inserted in max-heap, then it will be inserted at the last level.
To create the worst case scenario, let’s suppose that newly inserted key is the greatest element among all,
that are present in the max-heap. In this scenario, the newly inserted element will go to the top
i.e. the height of the max-heap which is nothing but O(log n).
So, in worst case, the INSERT(A, key) will take O(log(n)).
With this conclusion Option A & C gets eliminated, because option A is saying Insert(A, key) will take O(1) &
option C is saying Insert(A, key) will take O(n).
Now, we are left with option B & option D.
Now, let’s consider EXTRACT-MAX(A) : As A is a max -heap. So, maximum element is present at the
root itself.
To extract the maximum element the root node element is swapped with the last element & then the
maximum element can easily be extracted. This swapping operation can be done in O(1).
But in question it is mentioned that “The properties of a max-heap are preserved at the end of each of these operations.”
Means, after swapping, we have to call Max- Heapify(A,1) function to maintain the properties of max-heap.
This operation will take O(log n).
Overall time will be : O(1 + log n) = O(log n).
So, in this case also, EXTRACT-MAX(A) will take O(log(n)). |
And, Option D is saying EXTRACT-MAX(A) can be done in O(1). So, option D is also rejected.
Now, we are only left with one option, option B, which is the correct answer.
Both EXTRACT-MAX(A) & INSERT(A, key) run in O(log(n)).
Q4: Which one of the following sequences when stored in an array at locations A[1], . . . , A[10] forms a max-heap? (2023)
(a) 23,17,10, 6, 13, 14, 1, 5, 7, 12
(b) 23,17,14,7,13,10,1,5, 6,12
(c) 23, 17, 14, 6, 13, 10, 1, 5, 7, 15
(d) 23, 14, 17, 1, 10, 13, 16, 12, 7, 5
Ans: (b)
Sol: Option (A) is wrong here because node 14 comes after node 10
- Option (B) is a correct representation of the max heap. Option
- (C) is wrong here because node 15 comes after node 13 .
- Option (D) is wrong here because node 12 comes after node 1 .
Note: Here we insert the given value one by one and check whether the value at root node ≥ to its children as a max heap, also it should be a complete binary tree.
The max heap representation of option (B) is as follows: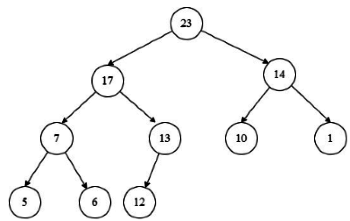
Q5: Let H be a binary min-heap consisting of n elements implemented as an array. What is the worst case time complexity of an optimal algorithm to find the maximum element in H? (2021 SET 2)
(a) Θ(1)
(b) Θ(log n)
(c) Θ(n)
(d) Θ(n log n)
Ans: (c)
Sol: In a min heap, maximum element is present in one of the leaf nodes.
If index of heap starts with 1 , indices of leaves are ⌊n/2⌋ + 1,⌊ n /2⌋ + 2 ,⌊ n /2⌋+3 … n .
So, we have to perform linear search on at most n /2+1 elements to find the maximum element. (we cannot perform binary search since it is not guaranteed that leaves are in sorted order) and that multiplied by some constant c will be the time complexity of the optimal algorithm. (Here, c includes the cost of all operations which includes comparison, index shift etc. for a single maximum element compare)
Q6: Consider the array representation of a binary min-heap containing 1023 elements. The minimum number of comparisons required to find the maximum in the heap is ___________. (2020)
(a)512
(b) 511
(c)1022
(d) 10
Ans: (b)
Sol: If a heap has 1023 elements, it'll contain 512 leaves and since it is a MIN-HEAP, the maximum will be present in the leaves. (Why? Assume it is not, then there will be some elements present under it and this will violate the min-heap property.)
We can visualize it this way. At each level starting with root level, number of elements are
1 − 2 − 4 − 8 − 16 − 32 − 64 − 128 - 256 − 512 (this is the last level, hence leaves)
So if we have n elements in an array, we know that to find the maximum it takes n − 1 comparisons.
In this case, n = 512 , so the answer should be 511 .
Some other excellent questions on finding maximum-minimum:
Q7: Consider the following statements: (2019)
I. The smallest element in a max-heap is always at a leaf node.
II. The second largest element in a max-heap is always a child of the root node.
III. A max-heap can be constructed from a binary search tree in Θ(n) time.
IV. A binary search tree can be constructed from a max-heap in Θ(n) time.
Which of the above statements is/are TRUE?
(a) I, II and III
(b) I, II and IV
(c) I, III and IV
(d) II, III and IV
Ans: (a)
Sol: The smallest element in a max-heap is always at a leaf node – TRUE because by definition of a max-heap every parent node must be larger than its child node.
The second largest element in a max-heap is always a child of a root node – TRUE. The kth largest element cannot have more than k−1 parents (larger value nodes) and so cannot be lower than level k .
A max-heap can be constructed from a binary search tree in Θ(n) time. Build heap for any array of size n (even unsorted) can be done in O(n ) time.
Now lets see the 4thstatement.
A binary search tree can be constructed from a max-heap in Θ(n) time. This can be proved FALSE using the simple argument that we can do max-heap construction in O(n) and if we can convert this to BST in O(n) time we can do an in order traversal of BST in O(n) time and thus we manage to sort n elements in O(n) time using just comparisons which is known to take at least Ω (n log n ) time.
An example construction of BST from a max-heap.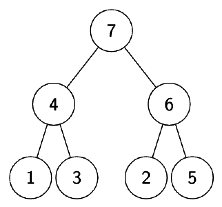
Max – Heap
Max Heap Array Representation:
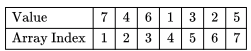 Make binary search tree using Array Representation:
Make binary search tree using Array Representation:
1. Pick elements from A[1]to A[7] one by one.
2. Compare with all previous elements and find its respective place.
We’ll get Binary Search Tree as follows:
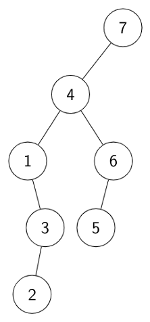
Number of comparisons in the worst case for each element =
So for n element heap the total no of comparisons could be = 0 + 1 + 2 +...(n - 2) + (n - 1)
Θ(n - 1)n/2
Θ(n2)
Note: Option IV: Proof by contradiction: Say you can somehow convert any arbitrary heap into a BST in O(n) time.
It is already known that any arbitrary list can be converted into a heap in O ( n ) time, and that the in-order traversal of BST is always sorted. So effectively we have sorted the array in linear time using comparison based sorting technique, but that is not possible as any comparison based sorting requires Ω (n log n) time. That is a contradiction.
By using more efficient method this time complexity could be reduced to O( n . log n ) but it can never be O(n) .
Q8: The number of possible min-heaps containing each value from {1, 2,3,4,5,6,7} exactly once is _____. (2018)
(a) 7
(b) 16
(c) 240
(d) 80
Ans: (d)
Sol: 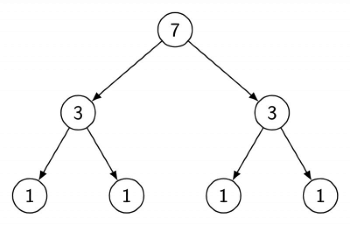
Now do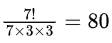
Here 7! because 7 items to be filled, Now 7 because root has only 7 nodes as its decedent including itself and only one can be the root. In same way we get 3 and 3 for the second level nodes and 1 and 1 for the third level.
Q9: A complete binary min-heap is made by including each integer in [1,1023] exactly once. The depth of a node in the heap is the length of the path from the root of the heap to that node. Thus, the root is at depth 0. The maximum depth at which integer 9 can appear is_____. (2016 SET 2)
(a) 9
(b) 8
(c) 1022
(d) 1021
Ans: (b)
Sol: Here answer is 8 .With 1023 nodes, we can easily build a min heap as shown in the below diagram.
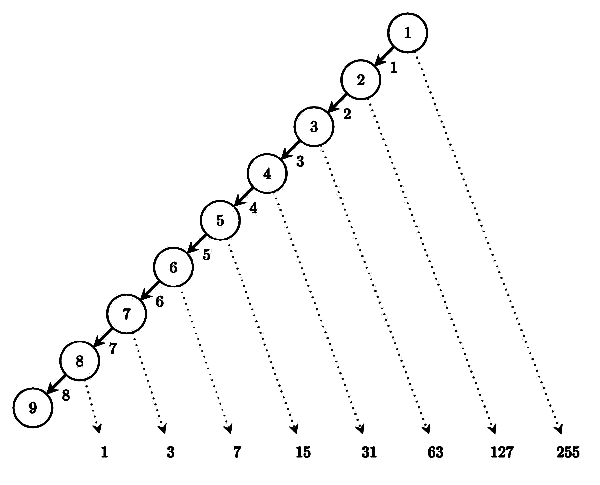 Here, 9 is pushed to the deepest possible level which is 8 here. (kth smallest element in a min-heap cannot go deeper than level k because the path from root to that level goes through k −1 smaller elements). Now, do we have enough elements to fill the right subtree to satisfy the complete binary tree property required by a heap? Yes. As shown in the diagram, up to depth 9 (assume it is fully filled) we’ll need 29−1 = 511 elements. We have 1023 elements and so the remaining 512 elements should go to depth 9 which is guaranteed to have the maximum element – here 1023.
Here, 9 is pushed to the deepest possible level which is 8 here. (kth smallest element in a min-heap cannot go deeper than level k because the path from root to that level goes through k −1 smaller elements). Now, do we have enough elements to fill the right subtree to satisfy the complete binary tree property required by a heap? Yes. As shown in the diagram, up to depth 9 (assume it is fully filled) we’ll need 29−1 = 511 elements. We have 1023 elements and so the remaining 512 elements should go to depth 9 which is guaranteed to have the maximum element – here 1023.
Q10: An operator delete(i) for a binary heap data structure is to be designed to delete the item in the i- th node. Assume that the heap is implemented in an array and i refers to the i-th index of the array. If the heap tree has depth d (number of edges on the path from the root to the farthest leaf),the n what is the time complexity to re-fix the heap efficiently after the removal of the element? (2016 SET 1)
(a) O(1)
(b) O(d) but not O(1)
(c) O(2d) but not O(d)
(d) O(d 2d) but not O(2d)
Ans: (b)
Sol: 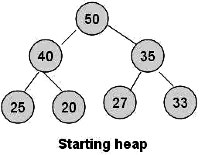
here d = 2 now in worst case root i.e. 50 will be deleted. so max 2(and 2 comparison needed) swap needed . so for d length O(d) time will be needed .
since O(1) is also given b/c if we delete leaf node i.e. 33 then no need to do anything.
Q11: Consider the following array of elements.
(89,19,50,17,12,15,2,5,7,11,6,9,100)
The minimum number of interchanges needed to convert it into a max-heap is (2015 SET 3)
(a) 4
(b) 5
(c) 2
(d) 3
Ans: (d)
Sol:
Interchanges:
- 1st 15-100
- 2nd 50-100
- 3rd 89- 100
Total interchange 3 so option (D) is correct.
Q12: Consider a complete binary tree where the left and the right subtrees of the root are max-heaps. The lower bound for the number of operations to convert the tree to a heap is (2015 SET 2)
(a) Ω(log n)
(b) (n)
(c) Ω(n logn)
(d) Ω(n2)
Ans: (a)
Sol: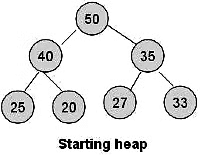
now to make it max heap it take only 2 swap and 2 comparison which is nothing but its height.
so log n time needed.
Q13: Consider a max heap, represented by the array: 40, 30, 20, 10, 15, 16, 17, 8, 4. (2015 SET 1)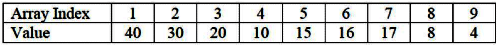 Now consider that a value 35 is inserted into this heap. After insertion, the new heap is
Now consider that a value 35 is inserted into this heap. After insertion, the new heap is
(a) 40,30,20,10,15,16,17,8,4,35
(b) 40,35,20,10,30,16,17,8,4,15
(c) 40,30,20,10,35,16,17,8,4,15
(d) 40,35,20,10,15,16,17,8,4,30
Ans: (b)
Sol: Heap is complete binary tree. To insert a new element, we put it at the end of the tree and move up towards root till heap property is satisfied. Here, 35comes as child of 15 , with the path
40 − 30 − 15 − 35. So, we swap 15 ,35 and then 30,35 to get the new path
40 − 35 − 30 − 15 . So, new heap will be 40, 35, 20, 10, 30, 16, 17, 8, 4, 15 .
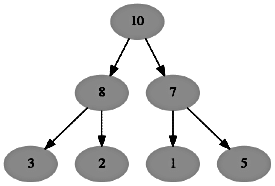
Q14: A priority queue is implemented as a Max-Heap. Initially, it has 5 elements. The level-order traversal of the heap is: 10, 8, 5, 3, 2. Two new elements 1 and 7 are inserted into the heap in that order. The level-order traversal of the heap after the insertion of the elements is: (2014 SET 2)
(a) 10, 8, 7, 3, 2, 1, 5
(b) 10, 8, 7, 2, 3,1, 5
(c) 10, 8, 7, 2, 3, 1, 5
(d) 10, 8, 7, 5, 3, 2, 1
Ans: (a)
Sol: whenever insertion will be done in heap ,it will always inserted in last level from left to right.so we insert 1 and 7 as a child of node 5 now we perform heapify algorithm until heap property will satisfied . and then we get the heap whose level order traversal is 10, 8, 7, 3, 2, 1, 5 .
Initial heap
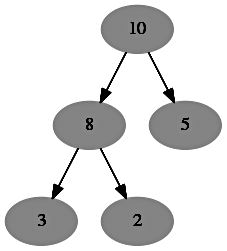
After insert of 1
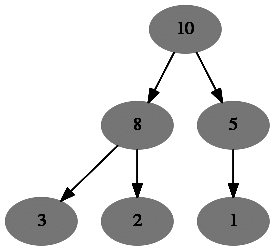
After insert of 7
Q15: A max-heap is a heap where the value of each parent is greater than or equal to the value of its children. Which of the following is a max-heap? (2011)
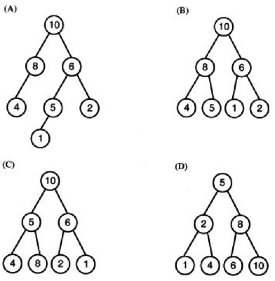
(a) A
(b) B
(c) C
(d) D
Ans: (b)
Sol: In option (A) - it is not a max heap because it is not a Complete Binary Tree (a heap must have all levels till last but one completely filled and in the last level all nodes must be filled from the left end without a gap till the last node)
In option (C) - it is complete binary tree but is not following the max heap property i.e. the value of parent node is not always greater than the child nodes as the node of value 5 is less then one of its child node value of 8.
In option (D) - similar to (C) option explanation here node of value 2 is less than the child node value 4
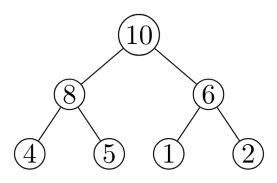 Correct option is (B) and it satisfies all the properties of a max heap.
Correct option is (B) and it satisfies all the properties of a max heap.
Q16: Consider a binary max-heap implemented using an array.
What is the content of the array after two delete operations on {25,14,16,13,10,8,12} (2009)
(a) {14, 13, 12, 10, 8}
(b) {14, 12, 13, 8, 10}
(c) {14, 13, 8, 12, 10}
(d) {14, 13, 12, 8, 10}
Ans: (d)
Sol: During delete, the root element is removed, replaced with the last element and heap property is corrected by pushing the root downwards. So, for first delete,
25 14 16 13 10 8 12→12 14 16 13 10 8→16 14 12 13 10 8 (the element not satisfying max-heap property is exchanged with the largest of its children) (heap property satisfied)
Second delete:
16 14 12 13 10 8→8 14 12 13 10→14 8 12 13 10→14 13 12 8 10 (heap property satisfied)
Q17: Consider a binary max-heap implemented using an array.
Which one of the following array represents a binary max-heap? (2009)
(a) {25,12,16,13,10,8,14}
(b) {25,14,13,16,10,8,12}
(c) {25,14,16,13,10,8,12}
(d) {25,14,12,13,10,8,16}
Ans: (c)
Sol: The binary max-Heap looks like this :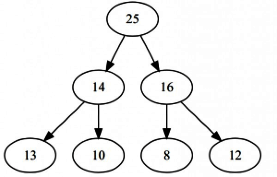 Max-Heap
Max-Heap
Q18: We have a binary heap on n elements and wish to insert n more elements (not necessarily one after another) into this heap. The total time required for this is (2008)
(a) Θ(log n)
(b) Θ(n)
(c) Θ(n log n)
(d) Θ(n2)
Ans: (b)
Sol: An insert operation on a binary heap takes O(log n) time, but an alternative approach we can use. which requires us to insert n elements in heap without any computation i.e. in constant time. after which we can apply Heapify operation(this operation creates heap in linear time) on the array of those element and Hence obtain a Heap in O(n) time.
Here "not necessarily one after another" should mean that we can insert n elements at once and not necessarily have to wait for first insert to be completed before doing second.
Q19: Consider the process of inserting an element into a Max Heap, where the Max Heap is represented by an array. Suppose we perform a binary search on the path from the new leaf to the root to find the position for the newly inserted element, the number of comparisons performed is: (2007)
(a) Θ (logn)
(b) Θ (loglogn)
(c) Θ (n)
(d) Θ (nlog2n )
Ans: (c)
Sol: Number of elements in the path from new leaf to root = log n , and all elements are sorted from leaf to root so we can do a binary search which will result in O(log log n) number of comparisons.
Since a heap is a complete binary tree (hence height balanced also), in an array implementation, from every node index, we can know its depth and this will be the number of elements − n for binary search
Q20: Which of the following sequences of array elements forms a heap? (2006)
(a) {23,17,14,6,13,10,1,12,7,5}
(b) {23,17,14,6,13,10,1,5,7,12}
(c) {23,17,14,7,13,10,1,5,6,12}
(d) {23,17,14,7,13,10,1,12,5,7}
Ans: (c)
Sol: For a heap(max heap) parent should be greater than or equal to children. in a heap of [1. . n] left child of ith node will be at 2 ∗ ith position and right child will be at 2 ∗ i + 1 position. So, for given options we can verify it. .
Q21: A 3-ary max heap is like a binary max heap, but instead of 2 children, nodes have 3 children. A 3-ary heap can be represented by an array as follows: The root is stored in the first location, a[0], nodes in the next level, from left to right, is stored from a[1] to a[3]. The nodes from the second level of the tree from left to right are stored from a[4] location onward. An item x can be inserted into a 3-ary heap containing n items by placing x in the location a[n] and pushing it up the tree to satisfy the heap property.
Suppose the elements 7, 2, 10 and 4 are inserted, in that order, into the valid 3-ary max heap found in the above question, Which one of the following is the sequence of items in the array representing the resultant heap? (2006)
(a) 10, 7, 9, 8, 3, 1, 5, 2, 6, 4
(b) 10, 9, 8, 7, 6, 5, 4, 3, 2, 1
(c) 10, 9, 4, 5, 7, 6, 8, 2, 1, 3
(d) 10, 8, 6, 9, 7, 2, 3, 4, 1, 5
Ans: (a)
Sol: 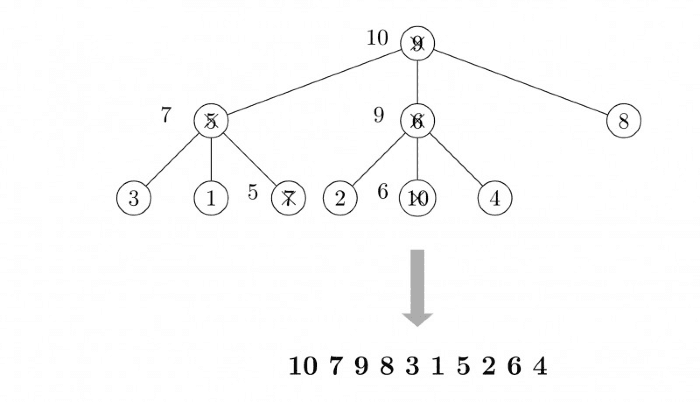 Correct answer A
Correct answer A
Q22: A 3-ary max heap is like a binary max heap, but instead of 2 children, nodes have 3 children. A 3-ary heap can be represented by an array as follows: The root is stored in the first location, a[0], nodes in the next level, from left to right, is stored from a[1] to a[3]. The nodes from the second level of the tree from left to right are stored from a[4] location onward. An item x can be inserted into a 3-ary heap containing n items by placing x in the location a[n] and pushing it up the tree to satisfy the heap property.
Which one of the following is a valid sequence of elements in an array representing 3-ary max heap? (2006)
(a) 1, 3, 5, 6, 8, 9
(b) 9, 6, 3, 1, 8, 5
(c) 9, 3, 6, 8, 5, 1
(d) 9, 5, 6, 8, 3, 1
Ans: (d)
Sol: The method to solve is clearly given in the question itself. Just one thing to mention is the heap property. Max Heap = The parent is always greater or equal to the child. if not then swap the respective child with the parent to satisfy the property of the heap.
Q23: In a binary max heap containing n numbers, the smallest element can be found in time (2006)
(a) Θ(n)
(b) Θ(logn)
(c) Θ(loglogn)
(d) Θ(1)
Ans: (a)
Sol: The above statement is actually algorithm for building a Heap of an input array A.
Upper bound of time complexity is O(n) for above algo
Q24: A Priority-Queue is implemented as a Max-Heap. Initially, it has 5 elements. The level-order traversal of the heap is given below:
10, 8, 5, 3, 2
Two new elements '1' and '7' are inserted in the heap in that order. The level-order traversal of the heap after the insertion of the elements is: (2005)
(a) 10, 8, 7, 5, 3, 2, 1
(b) 10, 8, 7, 2, 3, 1, 5
(c) 10, 8, 7, 1, 2, 3, 5
(d) 10, 8, 7, 3, 2, 1,5
Ans: (d)
Sol: whenever insertion will be done in heap ,it will always inserted in last level from left to right.so we insert 1 and 7 as a child of node 5 now we perform heapify algorithm until heap property will satisfied . and then we get the heap whose level order traversal is 10, 8, 7, 3, 2, 1, 5 .
Initial heap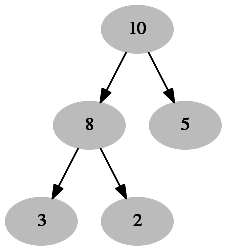
After insert of 1
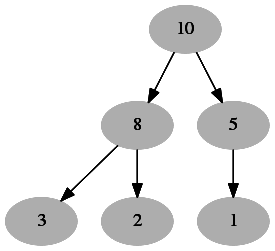
After insert of 7
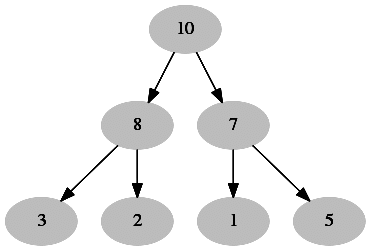
Q25: An array of integers of size n can be converted into a heap by adjusting the heaps rooted at each internal node of the complete binary tree starting at the node [( n − 1)/2] and doing this adjustment up to the root node (root node is at index 0) in the order [(n −1)/2], [(n − 3)/2], ....., 0. The time required to construct a heap in this manner is (2004)
(a) O (log n)
(b) O(n)
(c) O(n log log n)
(d) O(n log n)
Ans: (b)
Sol: By using Build Heap method we can create heap from complete binary tree. which will take O(n) .
Q26: The elements 32, 15, 20, 30, 12, 25, 16, are inserted one by one in the given order into a Max Heap. The resultant Max Heap is (2004)
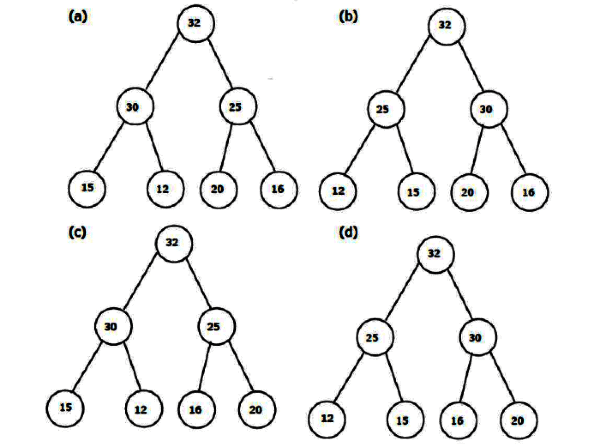 (a) A
(a) A
(b) B
(c) C
(d) D
Ans: (a)
Sol:  Just keep inserting elements making sure resulting Tree is nearly Complete. (Heap Property) .
Just keep inserting elements making sure resulting Tree is nearly Complete. (Heap Property) .
While inserting any node, if you find that Value of New Node > Value of its parent, bubble it up to keep Max heap property
Q27: A data structure is required for storing a set of integers such that each of the following operations can be done in O(logn) time, where n is the number of elements in the set. (2003)
1. Deletion of the smallest element.
2. Insertion of an element if it is not already present in the set.
Which of the following data structures can be used for this purpose ?
(a) A heap can be used but not a balanced binary search tree
(b) A balanced binary search tree can be used but not a heap
(c) Both balanced binary search tree and heap can be used
(d) Neither balanced binary search tree nor heap can be used
Ans: (b)
Sol: Balanced search tree have height log n
Deletion of smallest element will take O(log n) time
Finding a element is present/not and doing insertion: O(log n)
Heap(MIN) is also an almost complete binary tree have height log n
Deletion of smallest element will take O(log n) time (root element removal, replace with last element +balancing)
Finding a element is present/not and insertion: Finding only takes O(n) , insertion then balancing take O(log n) .
So, total O(n) + O(log n) = O(n).
(even if its maxheap our ans. does not change only time for deletion of min will increase O(n))
Q28: In a heap with n elements with the smallest element at the root, the 7th smallest element ban be found in time (2003)
(a) Θ(n log n)
(b) Θ (n)
(c) Θ(log n)
(d) Θ(1)
Ans: (d)
Sol: Time to find the smallest element on a min-heap- one retrieve operation - Θ(1)Time to find the second smallest element on a min-heap- requires 22 − 1 = 3 check operations to find the second smallest element out of 3 elements - Θ(1)
Time to find the 7th smallest element - requires O( 27− 1) = O(127) check operations to find the seventh smallest element out of 127 possible ones - Θ(1)
In short if the number of required operations is independent of the input size n , then it is always Θ(1) .
(Here, we are doing a level order traversal of the heap and checking the elements)
If we are not allowed to traverse the heap and allowed only default heap-operations, we will be restricted with doing Extract-min 7 times which would be O(log n)
Q29: Consider any array representation of an n element binary heap where the elements are stored from index 1 to index n of the array.
For the element stored at index i of the array ( i ≤ n) , the index of the parent is (2001)
(a) i-1
(b) [i/2]
(c) i/2
(d) (i+1)/2
Ans: (b)
Sol: for node at index i
left child (L) at 2i
right child (R) at 2i + 1
for node at index i
parent will be at floor i/2
Q30: The minimum number of interchanges needed to convert the array into a max-heap is (1996)
89, 19, 40, 17, 12, 10, 2, 5, 7, 11, 6, 9, 70
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (c)
Sol:
"The minimum number of interchanges needed to convert the array
89, 19, 40, 17, 12, 10, 2, 5, 7, 11, 6, 9, 70
into a heap with the maximum element at the root node is:"
This is the correction.
Answer: C.
Only element 70 violates the rule. Hence, it must be shifted to its proper position.
Step1: swap (10, 70)
Step2: swap (40, 70)
Hence, only 2 interchanges are required.
|
158 docs|30 tests
|
FAQs on Previous Year Questions: Heap Tree - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is a Heap Tree in computer science? |  |
| 2. How is a Heap Tree different from a regular binary tree? |  |
| 3. What are the applications of Heap Trees in computer science? |  |
| 4. How can a Heap Tree be implemented in programming languages like C++ or Java? |  |
| 5. What is the time complexity of basic operations in a Heap Tree, such as insertion, deletion, and retrieval? |  |





















