Q1: If the energy of a continuous-time signal x(t) is E and the energy of the signal 2x(2t − 1) is cE, then c is ______ (rounded off to 1 decimal place). (2024)
(a) 1.2
(b) 2
(c) 2.6
(d) 3.2
Ans: (b)
Sol: 
Q2: Consider the discrete-time system T1 and T2 defined as follows:
 Which one of the following statement is true? (2024)
Which one of the following statement is true? (2024)
(a) T1 and T2 are BIBO stable.
(b) T1 and T2 are not BIBO stable.
(c) T1 is BIBO stable butT2 is not BIBO stable.
(d) T1 is not BIBO stable but T2 is BIBO stable.
Ans: (d)
Sol: 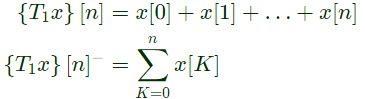 Let,
Let,


 Let,
Let,

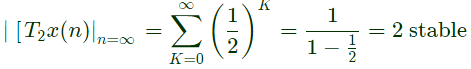 T1 is not BIBO stable but T2 is BIBO stable.
T1 is not BIBO stable but T2 is BIBO stable.
Q3: Suppose signal y(t) is obtained by the time-reversal of signal x(t), i.e., y(t) = x(−t), -∞
ltt
lt∞. Which one of the following options is always true for the convolution of x(t) and y(t) ? (2024)
(a) It is an even signal.
(b) It is an odd signal.
(c) It is a causal signal.
(d) It is an anti-causal signal.
Ans: (a)
Sol: 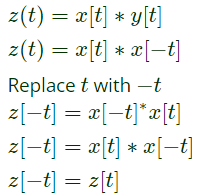 even function.
even function.
Q4: The period of the discrete-time signal x[n] described by the equation below is N = ___ (Round off to the nearest integer). (2023)
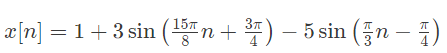 (a) 16
(a) 16
(b) 32
(c) 48
(d) 64
Ans: (c)
Sol: Given :






Q5: For the signals x(t) and y(t) shown in the figure, z(t) = x(t) ∗ y(t) is maximum at t = T1. Then T1 in seconds is (Round off to the nearest integer). (2023)
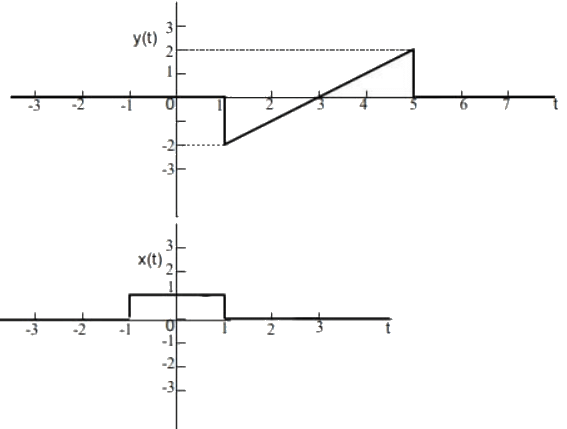 (a) 2
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (c)
Sol: Using convotution property
z(t) = x(t) ∗ y(t)

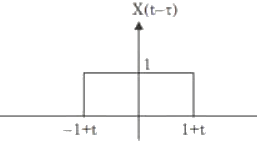 For max. overlap
For max. overlap


Q6: Two discrete-time linear time-invariant systems with impulse responses h1[n] = δ[n − 1] + δ[n + 1] and h2[n] = δ[n] + δ[n − 1] are connected in cascade, where δ[n] is the Kronecker delta. The impulse response of the cascaded system is (2021)
(a) δ[n − 2] + δ[n + 1]
(b) δ[n − 1]δ[n] + δ[n + 1]δ[n − 1]
(c) δ[n − 2] + δ[n − 1] + δ[n] + δ[n + 1]
(d) δ[n] δ[n − 1] + δ[n − 2] δ[n + 1]
Ans: (c)
Sol: 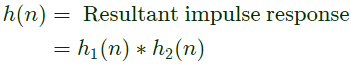 By applying z -transform
By applying z -transform
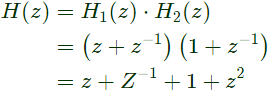 By applying inverse ZT,
By applying inverse ZT,

Q7: Suppose for input x(t) a linear time-invariant system with impulse response h(t) produces output y(t), so that x(t) ∗ h(t) = y(t). Further, if x(t)∣ ∗ ∣h(t)∣ = z(t), which of the following statements is true? (2020)
(a) For all t ∈ (−∞, ∞), z(t) ≤ y(t)
(b) For some but not all t ∈ (−∞, ∞), z(t) ≤ y(t)
(c) For all t ∈ (−∞, ∞), z(t) ≥ y(t)
(d) For some but not all t ∈ (−∞, ∞), z(t) ≥ y(t)
Ans: (c)
Sol: 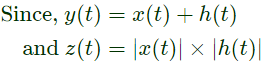 Case-1:
Case-1:
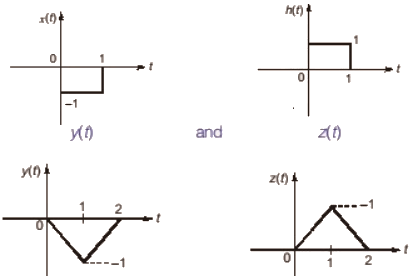 case 2:
case 2:
 then, y(t) = z(t)
then, y(t) = z(t)
 Thus, z(t) ≥ y(t), for all ’t’ .
Thus, z(t) ≥ y(t), for all ’t’ .
Q8: The symbols, a and T, represent positive quantities, and u(t) is the unit step function. Which one of the following impulse responses is NOT the output of a causal linear time-invariant system? (2019)
(a) e+atu(t)
(b) e−a(t+T)u(t)
(c) 1+e−atu(t)
(d) e−a(t−T)u(t)
Ans: (c)
Sol: a and T represents positive quantities.
u(t) is unit step function.
h(t) = 1+e−atu(t), is non-causal
Here '1' is a constant and two sided so the system will be non-causal, because for causal system,

Q9: The signal energy of the continuous-time signal x(t) = [(t − 1)u(t − 1)] − [(t − 2)u(t − 2)] − [(t − 3)u(t − 3)] + [(t − 4)u(t − 4)] is (2018)
(a) 11/3
(b) 7/3
(c) 1/3
(d) 5/3
Ans: (d)
Sol: x(t) = r(t − 1) − r(t − 2) − r(t − 3) + r(t − 4)



Q10: The mean square value of the given periodic waveform f(t) is_________ (SET-2 (2017))
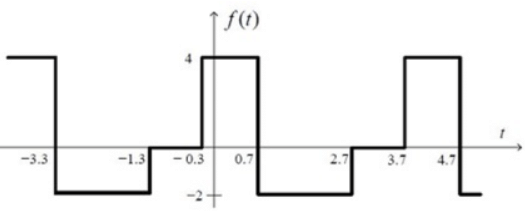 (a) 12
(a) 12
(b) 24
(c) 6
(d) 3
Ans: (c)
Sol: Mean square value = power of f(t)
Mean square value

Q11: Consider the system with following input-output relation y[n] = (1 + (−1)n)x[n] where, x[n] is the input and y[n] is the output. The system is (SET-1 (2017))
(a) invertible and time invariant
(b) invertible and time varying
(c) non-invertible and time invariant
(d) non-invertible and time varying
Ans: (d)
Sol: Given relationship,
y(n) = [1+(−1)n]x(n)
Time invariance test:
 Since, y(n−1) ≠ y′(n)
Since, y(n−1) ≠ y′(n)
So, the system is time invariant.
Invertibility test:
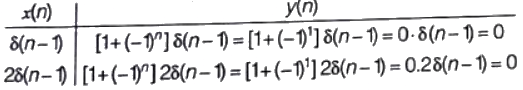 Thus, we are getting many to one mapping between input and output. So, the system is non-invertible.
Thus, we are getting many to one mapping between input and output. So, the system is non-invertible.
Q12: The value of 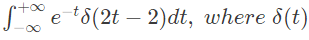 is the Dirac delta function, is (SET-1 (2016))
is the Dirac delta function, is (SET-1 (2016))
(a) 1/2e
(b) 2/e
(c) 1/e2
(d) 1/2e2
Ans: (a)
Sol: To find the value of 
Since, 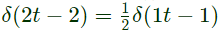 above integral can be written as
above integral can be written as

Q13: The function shown in the figure can be represented as (SET-1 (2014))
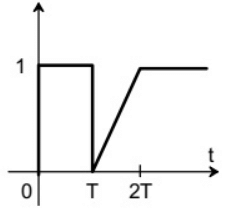 (a)
(a) 
(b) 
(c) 
(d) 
Ans: (a)
Sol:  The given function can be realized as follow:
The given function can be realized as follow:


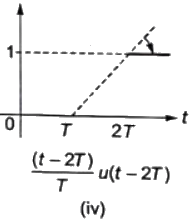 Combining the function (i0, (ii), (iii) and (iv), we get the given function
Combining the function (i0, (ii), (iii) and (iv), we get the given function
 Therefore,
Therefore,

Q14: A zero mean random signal is uniformly distributed between limits -a and +a and its mean square value is equal to its variance. Then the r.m.s value of the signal is (2011)
(a) a/√3
(b) a/√2
(c) a√2
(d) a√3
Ans: (a)
Q15: Given a sequence x[n], to generate the sequence y[n] = x[3 - 4n], which one of the following procedures would be correct ? (2008)
(a) First delay x[n] by 3 samples to generate z1[n], then pick every 4th sample of z1[n] to generate z2[n], and than finally time reverse z2[n] to obtain y[n].
(b) First advance x[n] by 3 samples to generate z1[n], then pick every 4th sample of z1[n] to generate z2[n], and then finally time reverse z2[n] to obtain y[n]
(c) First pick every fourth sample of x[n] to generate v1[n], time-reverse v1[n] to obtain v2[n], and finally advance v2[n] by 3 samples to obtain y[n]
(d) First pick every fourth sample of x[n] to generate v1[n], time-reverse v1[n] to obtain v2[n], and finally delay v2[n] by 3 samples to obtain y[n]
Ans: (b)
Sol: y[n] = x[3 − 4n] = x[−4n + 3]
So to obtain y[n], we first advance x[n] by 3 unit.
i.e. z1[n] = x[n + 3]
Now we will take every fourth sample of z1[n]
i.e. z2[n] = z1[4n] = x[4n + 3]
Now reverse (time reverse) z2[n] will give
y[n] = z2[−n] = x[−4n + 3]
Q16: A continuous-time system is described by y(t) = e−∣x(t)∣, where y(t) is the output and x(t) is the input. y(t) is bounded (2006)
(a) only when x(t) is bounded
(b) only when x(t) is non-negative
(c) only for t ≥ 0 if x(t) is bounded for t ≥ 0
(d) even when x(t) is not bounded
Ans: (d)
Q17: Which of the following is true? (2006)
(a) A finite signal is always time bounded
(b) A time bounded signal always possesses finite energy
(c) A bounded signal is always zero outside the interval [−t0, t0 ] for some t0
(d) A time bounded signal is always finite
Ans: (d)
Q18: What is the rms value of the voltage waveform shown in figure? (2002)
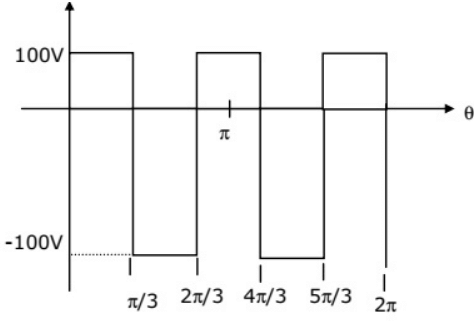 (a) (200/π) V
(a) (200/π) V
(b) (100/π) V
(c) 200V
(d) 100V
Ans: (d)
Sol: RMS value

Q19: A current impulse 5δ(t), is forced through a capacitor C. The voltage Vc(t), across the capacitor is given by (2002)
(a) 5t
(b) 5u(t) - C
(c) (5/C) (t)
(d) 5u(t)/C
Ans: (d)
Sol: 

 Which one of the following statement is true? (2024)
Which one of the following statement is true? (2024)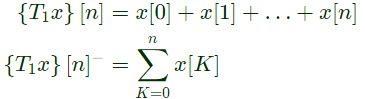 Let,
Let,

 Let,
Let,
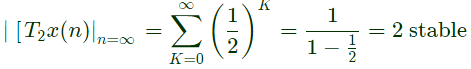 T1 is not BIBO stable but T2 is BIBO stable.
T1 is not BIBO stable but T2 is BIBO stable.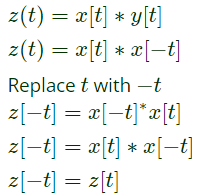 even function.
even function.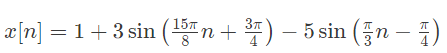 (a) 16
(a) 16





 (a) 2
(a) 2
 For max. overlap
For max. overlap

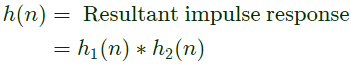 By applying z -transform
By applying z -transform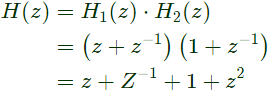 By applying inverse ZT,
By applying inverse ZT,
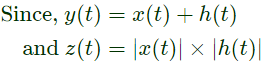 Case-1:
Case-1: case 2:
case 2: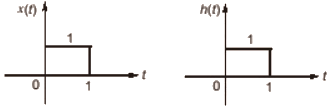 then, y(t) = z(t)
then, y(t) = z(t) Thus, z(t) ≥ y(t), for all ’t’ .
Thus, z(t) ≥ y(t), for all ’t’ .



 (a) 12
(a) 12
 Since, y(n−1) ≠ y′(n)
Since, y(n−1) ≠ y′(n)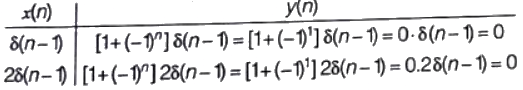 Thus, we are getting many to one mapping between input and output. So, the system is non-invertible.
Thus, we are getting many to one mapping between input and output. So, the system is non-invertible.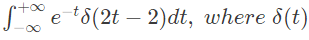 is the Dirac delta function, is (SET-1 (2016))
is the Dirac delta function, is (SET-1 (2016))
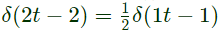 above integral can be written as
above integral can be written as
 (a)
(a) 



 The given function can be realized as follow:
The given function can be realized as follow:

 Combining the function (i0, (ii), (iii) and (iv), we get the given function
Combining the function (i0, (ii), (iii) and (iv), we get the given function Therefore,
Therefore,
 (a) (200/π) V
(a) (200/π) V






















