Previous Year Questions: Linear Algebra | Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE) PDF Download
Q1: Let A be an n × n matrix over the set of all real numbers R. Let B be a matrix obtained from A by swapping two rows. Which of the following statements is/are TRUE? (2024 SET-2)
(a) The determinant of A is the negative of the determinant of A
(b) If A is invertible, then B is also invertible
(c) If A is symmetric, then B is also symmetric
(d) If the trace of A is zero, then the trace of B is also zero
Ans: (a, b)
Sol: Let's take an example Determinant of A = 1x1 - 0x0 = 1
Determinant of A = 1x1 - 0x0 = 1
Determinant of B = 0x0 - 1x1
= -1
= -(Determinant of A)
Option B: True
If A is invertible, it means Determinant of A
|A| != 0
And,
Determinant of B = -(Determinant of A)
So,
|B| != 0, B is also Invertible.
Option C: False
Lets take an example Clearly, we can see that while A is symmetric, B is not.
Clearly, we can see that while A is symmetric, B is not.
Option D: False
Let's take an example. trace(A) = 1-2+1 = 0
trace(A) = 1-2+1 = 0
trace(B) = -1-1+1 = -1
trace(A) ! = trace(B)
Q2: Let xx and yy be random variables, not necessarily independent, that take real values in the interval [0,1]. Let z = xy and let the mean values of x, y, z be  respectively. Which one of the following statements is TRUE? (2024 SET-2)
respectively. Which one of the following statements is TRUE? (2024 SET-2)
(a)  (b)
(b) (c)
(c)  (d)
(d)  Ans: (d)
Ans: (d)
Sol: Lets first give counter example for (C) and (A):
Lets assume X is a random variable uniformly distributed in [0, 1] and Y is 1−X .
So, E(X) = 1/2
and E(Y) = E(1−X) = E(1)−E(X) = 1 − (1/2) = (1/2)
Now, Given Z = XY [Note here Covariance is negative]
[Note here Covariance is negative]
Counter Example for (B):
Lets assume X is a random variable uniformly distributed in [0, 1] and Y = X.
So, E(X) = 1/2
E(Y) = 1/2
Now Given Z = XY
So,  So, E(Z) ≥ E(X)E(Y)
So, E(Z) ≥ E(X)E(Y)
[Note here Covariance is positive]
Now , why does option (D) is correct ?
⇒ It is given , X and Y takes value in the range [0, 1].
So, we can write , 0 ≤ Y ≤ 1 .
Multiply this inequality by X.
So, 0 ≤ XY ≤ X
Now take expectation of this Inequality,
So, E(0) ≤ E(XY) ≤ E(X)
So, 0 ≤ E(XY) ≤ E(X)
Which proof the option (D) .
Note this inequality Holds true because X and Y takes value in the range between [0, 1].
Q3: Let A be any n × m matrix, where m > n. Which of the following statements is/are TRUE about the system of linear equations Ax = 0? (2024 SET-1)
(a) There exist at least m−n linearly independent solutions to this system
(b) There exist m − n linearly independent vectors such that every solution is a linear combination of these vectors
(c) There exists a non-zero solution in which at least m − n variables are 0
(d) There exists a solution in which at least n variables are non-zero
Ans: (a)
Sol: A: True
This option is similar to the question asked in GATE 2021:
B: False
It may be possible that every solution is a linear combination of more than m−n linearly independent vectors.
C: False
Consider The solution of this Ax = 0 is
The solution of this Ax = 0 is
We can see that there is no variable which is zero in a non-zero solution.
D: False
Consider The solution of this Ax = 0 is
The solution of this Ax = 0 is Option D says, There is a solution in which at least n(= 3) are non-zero. Since in the above system of linear equations only 2 are non-zero, hence it is also false.
Option D says, There is a solution in which at least n(= 3) are non-zero. Since in the above system of linear equations only 2 are non-zero, hence it is also false.
Q4: The product of all eigenvalues of the matrix  is (2024 SET-1)
is (2024 SET-1)
(a) -1
(b) 0
(c) 1
(d) 2
Ans: (b)
Sol: Product of eigen values is Determinant of the matrix.
Since, Columns are Linearly Dependent (C3 = 2*C2 - C1) we can say Determinant will be zero.
(B) is correct option.
Q5: Let A be the adjacency matrix of the graph with vertices {1, 2, 3, 4, 5}. Let λ1, λ2, λ3, λ4, and λ5 be the five eigenvalues of A. Note that these eigenvalues need not be distinct.
Let λ1, λ2, λ3, λ4, and λ5 be the five eigenvalues of A. Note that these eigenvalues need not be distinct.
The value of λ1 + λ2 + λ3 + λ4 + λ5 = _____ (2023)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
Sol: There are two possible choices for the adjacency matrix for the given undirected graph G and hence two possible answers.
Your first choice could be: The problem with this matrix is that Handshaking lemma is not satisfied here because sum of each row gives the total degree of each vertex and so here total degree = 12 and total edges in the graph is 7.
The problem with this matrix is that Handshaking lemma is not satisfied here because sum of each row gives the total degree of each vertex and so here total degree = 12 and total edges in the graph is 7.
The reason is, this matrix is made on the assumption that self-loop has degree 1 and that's why Handshaking Lemma will be failed here because the reason we take the degree of the self-loop as 2 to make Handshaking Lemma satisfied.
Hence, if we make the assumption that self-loop has degree 1 then the answer will be 2 because of self-loops, each with degree 1.
Now, your second choice could be: Here, Handshaking lemma is satisfied because total degree=14 because sum of all the rows is 14. and Hence, total number of edges is 7.
Here, Handshaking lemma is satisfied because total degree=14 because sum of all the rows is 14. and Hence, total number of edges is 7.
Again the reason is, this matrix is made on the assumption that self-loop has degree 2 and that's why Handshaking Lemma will be satisfied here because the reason we take the degree of the self-loop as 2 to make Handshaking Lemma satisfied.
Hence, if we make the assumption that self-loop has degree 2 then the answer will be 4 because of self-loops, each with degree 2.
Most probably, GATE Authority will give answer as 2 because the convention follows in most of the books whether it is Diestel, Bondy & Murthy, Douglas B. West, Narsingh Deo or Harary, All follows first convention but I have given the true picture so that all of you know about the issue with this question.
Edit: After challenge, answer has been changed from 2 to 2 or 4.
Q6: Let  Let det(A) and det(B) denote the determinants of the matrices A and B, respectively.
Let det(A) and det(B) denote the determinants of the matrices A and B, respectively.
Which one of the options given below is TRUE? (2023)
(a) det(A) = det(B)
(b) det(B) = - det(A)
(c) det(A) = 0
(d) det(AB) = det(A) + det(B)
Ans: (b)
Sol: the elements of both the matrix A, B are the same. in matrix B R1, R3 are interchanged.
as we know the important property of any determinants:
- if two rows (or 2 columns) of a determinant are interchanged the sign of the value of the determinant is changed.
here only one time rows is changed so the determinant should be multiplied by (−1).
∴ det(B) = −det(A)
Option (B) is correct.
Q7: Which of the following is/are the eigenvector(s) for the matrix given below? MSQ (2022)
MSQ (2022)
(a)  (b)
(b)  (c)
(c)  (d)
(d)  Ans: (a, c, d)
Ans: (a, c, d)
Sol: Ax = λx
Learn very powerful and important way to multiply matrix and vector. Ax is just linear combination of columns of A.. if you can understand this then solution of system of linear equation is just cakewalk for you. And complete linear algebra will come very intutive.
A. B.
B. C.
C.  D.
D. 
Q8: Consider solving the following system of simultaneous equations using LU decomposition.
x1 + x2 − 2x3 = 4
x1 + 3x2 − x3 = 7
2x1 + x2 − 5x3 = 7
where L and U are denoted as Which one of the following is the correct combination of values for L32, U33, and x1? (2022)
Which one of the following is the correct combination of values for L32, U33, and x1? (2022)
(a) L32 = 2, U33 = −1/2, x1 = −1
(b) L32 = 2, U33 = 2, x1 = −1
(c) L32 = −1/2, U33 = 2, x1 = 0
(d) L32 = −1/2, U33 = −1/2, x1 = 0
Ans: (d)
Sol: Given question is incorrect and all the other answers are also incorrect because question says one option is correct but both (C) and (D) are correct here.
You can decompose the coefficient matrix in two ways as following:
(1) So,
So,  (2)
(2) So, L32 = -1/2 and U33 = 2
So, L32 = -1/2 and U33 = 2
From the edit part at the end of this answer:
When x = y = z = 1, you get the first LU decomposition and when x = y = 1 and z = −1/4, you get the second LU decomposition.
Now you can apply the method (1) as given below and get the first LU decomposition and to obtain the second LU decomposition, you have to multiply third column of matrix L in first LU decomposition by −1/4 and divide the third row of matrix U in first LU decomposition by −1/4 as it is given in the below comment.
All the remaining things you can get from the rest of this answer.
_________________________________________________
Method 1(Shortcut):
Here, we do 3 elementary row operations on the following coefficient matrix A to get U as: Now, to get L, we just have to reverse the sign of the bold text which we have used in above row operations and put in that position of L for which we have used the above row operations.
Now, to get L, we just have to reverse the sign of the bold text which we have used in above row operations and put in that position of L for which we have used the above row operations.
For Example, we have used −1R1 + R2 to make the position of second row and first column as zero. So, L21 = 1. Similarly, −2R1 + R3 is used to make third row and first column as zero and so, L31 = 2 and 1/2R2 + R3 is used to make third row and second column as zero and so, L32 = −1/2. Since, diagonal elements of U are not all 1s and hence, all diagonal elements of L will be 1.
Hence,  Therefore, (D)
Therefore, (D)
If anyone wants to know why this works then reason lies in the third method below and you can see the results of  to know why it works.
to know why it works.
Method 2:
x1+x2−2x3 = 4(1)
x1+3x2−x3 = 7(2)
2x1+x2−5x3 = 7(3)
2eq(2)–eq(3) gives 5x2 + 3x3 = 7
2eq(1)–eq(3) gives x2 + x3=1 ⟹ 5x2 + 5x3 = 5
Solving 5x2 + 3x3 = 7 and 5x2 + 5x3 = 5 gives x3 = −1, x2 = 2 and by putting it in eq(1), we get, x1 = 0
So, x1 = 0, it means either option (C) is correct or (D)
Now, we only need to find U33 and get the answer for the given question.
To find LU decomposition (if it is possible), we only need to convert the given matrix into U by elementary row operations in Gaussian Elimination method (described at the end of the answer to find the complete solution for the given questions).
So, here,  After R2←R2–R1, A becomes
After R2←R2–R1, A becomes  After R3←R3–2R1, A becomes
After R3←R3–2R1, A becomes  After R3←R3+1/2R2, A becomes
After R3←R3+1/2R2, A becomes  So,
So,  It means
It means  It means U33 = -1/2
It means U33 = -1/2
Method 3:
Now, to find the complete solution for the given question, we can use this previous year question to find the LU decomposition and then find x1
After Applying R2←R2–R1, A becomes  and E21 becomes
and E21 becomes  After Applying R3←R3–2R1, A becomes
After Applying R3←R3–2R1, A becomes  and E31 becomes
and E31 becomes  After Applying R3←R3+1/2R2, A becomes
After Applying R3←R3+1/2R2, A becomes  and E32 becomes
and E32 becomes  So,
So,  and E32E31E21 (A) = U
and E32E31E21 (A) = U Hence,
Hence,  Now, to find x1, x2, x3, we can write:
Now, to find x1, x2, x3, we can write:
AX = B ⇒ LUX = B
let UX = Y, So, LY = B
we can write LY = B in matrix notation as: 
 So,
So, Now, on solving UX = Y i.e.
Now, on solving UX = Y i.e.  It means
It means Edit:
Edit:
LU decomposition is not necessarily unique if it exists.
Here, you can make infinitely many A = LU decomposition as: where x, y, z ∈ R for which det(L) and det(U) are non-zero because det(A) ≠ 0.
where x, y, z ∈ R for which det(L) and det(U) are non-zero because det(A) ≠ 0.
Now you can take x = 1, y = 2, z = 3 or x = 3, y = −1, z = 5 etc, you get the same coefficient matrix.
The reason is that you can make LU decomposition unique by imposing the constraints on either the diagonal entries of L or U.
You can make the above LU decomposition by assuming L11 = x, L22 = y, L33 = z and rest of the entries of L and U will automatically be obtained when you solve by solving equations after writing A = LU.
Another way is to assume U11 = x, U22 = y, U33 = z and you get a different LU decomposition.
Q9: Consider the following two statements with respect to the matrices Am×n,Bn×m,Cn×n and Dn×n,
Statement 1: tr(AB) = tr(BA)
Statement 2: tr(CD) = tr(DC)
wheretr()tr() represents the trace of a matrix. Which one of the following holds? (2022)
(a) Statement 1 is correct and Statement 2 is wrong.
(b) Statement 1 is wrong and Statement 2 is correct.
(c) Both Statement 1 and Statement 2 are correct.
(d) Both Statement 1 and Statement 2 are wrong.
Ans: (c)
Sol: Trace of a matrix and sum of eigen values of matrix are same.
AB and BA has same nonzero eigen values (Proof below) hence their sum of eigen values i.e. trace should also be same.
Proof-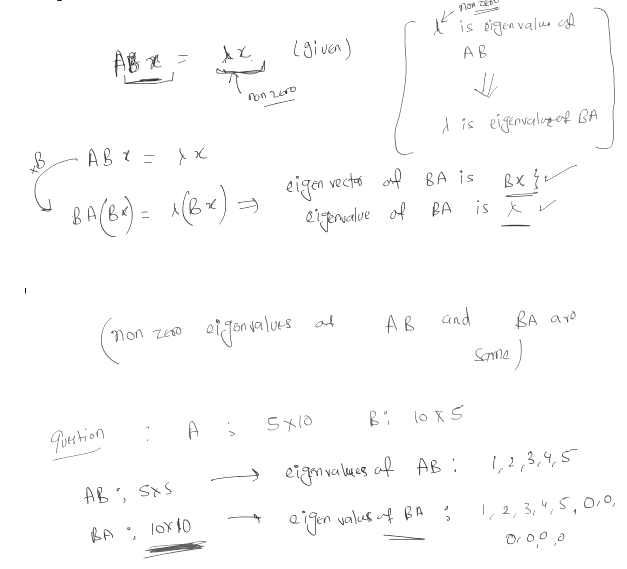
Q10: Suppose that P is a 4x5 matrix such that every solution of the equation Px = 0 is a scalar multiple of [2 5 4 3 1]T. The rank of P is _______ (2021 SET-2)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (d)
Sol: Every solution to Px = 0 is scalar multiple of [2 5 4 3 1]T, It means out of 5 column vectors of matrix P, 4 are linearly independent as we have only one line in NULL Space (along the given vector).
Rank is nothing but the number of linearly independent column vectors in a matrix which is 4 here.
Q11: Consider the following matrix. The largest eigenvalue of the above matrix is __________. (2021 SET-1)
The largest eigenvalue of the above matrix is __________. (2021 SET-1)
(a) 1
(b) 3
(c) 4
(d) 6
Ans: (b)
Sol: Let  Characteristic equation ∣A–λI∣ = 0
Characteristic equation ∣A–λI∣ = 0 Perform the operation, C4→C1+C2+C3+C4, we get
Perform the operation, C4→C1+C2+C3+C4, we get Perform the operation,
Perform the operation,
R1 → R1 − R4, R2 → R2 − R1, R3 → R3 − R1, we get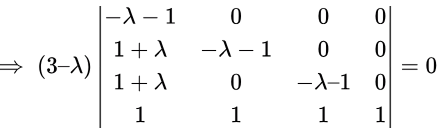
⇒ (3 - λ)(-λ -1)(-λ -1)(-λ -1) = 0
⇒ λ = −1, −1, −1, 3
∴ The largest eigenvalue is 3.
PS: For any matrix A,
- The determinant of A equals the product of its eigenvalues.
- The trace of A equals the sum of its eigenvalues.
- The trace of a matrix is defined as the sum of the leading diagonal entries.
- A real symmetric matrix has only real eigenvalues.
OR
Let  We can write given matrix as:
We can write given matrix as:  A Markov matrix is a square matrix with all nonnegative entries, and where the sum of the entries down any column is 1. If the entries are all positive, it’s a positive Markov matrix. It is also called a doubly stochastic matrix.The most important facts about a positive Markov matrix are:
A Markov matrix is a square matrix with all nonnegative entries, and where the sum of the entries down any column is 1. If the entries are all positive, it’s a positive Markov matrix. It is also called a doubly stochastic matrix.The most important facts about a positive Markov matrix are:
- λ = 1 is an eigenvalue.
- The eigenvector associated with λ = 1 can be chosen to be strictly positive.
- All other eigenvalues have a magnitude less than 1.
So, the correct answer is 3.
Q12: If x + 2y = 30, then  will be equal to (2020)
will be equal to (2020)
(a) 8
(b) 16
(c) 18
(d) 20
Ans: (b)
Sol:  Taking LCM we get:
Taking LCM we get: Option (B) is correct.
Option (B) is correct.
Q13: Let A and B be two nxn matrices over real numbers. Let rank(M) and det(M) denote the rank and determinant of a matrix M, respectively. Consider the following statements.
I. rank(AB) = rank (A)rank (B)
II. det(AB) = det(A)det(B)
III. rank(A+B) ≤ rank (A) + rank (B)
IV. det(A+B) ≤ det(A) + det(B)
Which of the above statements are TRUE? (2020)
(a) I and II only
(b) I and IV only
(c) II and III only
(d) III and IV only
Ans: (c)
Sol: Rank(AB) = min(Rank(A), Rank(B))
Det(AB) = Det(A) × Det(B)
Rank(A + B) ≤ Rank(A) + Rank(B). Because addition of two matrices can never result in increase in the number of independent columns and rows in the matrix.
Answer: C
Q14: Consider the following matrix: The absolute value of the product of Eigenvalues of R is _________ . (2019)
The absolute value of the product of Eigenvalues of R is _________ . (2019)
(a) 10
(b) 12
(c) 25
(d) 125
Ans: (b)
Sol: Important properties of Eigen values:
- Sum of all eigen values = Sum of leading diagonal(principle diagonal) elements = Trace of the matrix.
- Product of all Eigen values = det(A) = ∣A∣
- Any square diagonal(lower triangular or upper triangular) matrix eigen values are leading diagonal (principle diagonal)elements itself.
Example:  Diagonal matrix
Diagonal matrix
Eigenvalues are 1, 1, 1 Upper triangular matrix
Upper triangular matrix
Eigenvalues are 1, 1, 1 Lower triangular matrix
Lower triangular matrix
Eigenvalues are
Now coming to the actual question Perform
Perform
 Perform
Perform
 Perform
Perform
- R4 → R4 - R3
 The absolute value of product of Eigen values = set (A) = Product of diagonal element = 12.
The absolute value of product of Eigen values = set (A) = Product of diagonal element = 12.
Q15: Let X be a square matrix. Consider the following two statements on X.
I. X is invertible
II. Determinant of X is non-zero
Which one of the following is TRUE? (2019)
(a) I implies II; II does not imply I
(b) II implies I; I does not imply II
(c) I does not imply II; II does not imply I
(d) I and II are equivalent statements
Ans: (d)
Sol: Square Matrix is invertible iff it is non-singular.
So both statements are same.
Answer is (D).
Q16: Consider a matrix P whose only eigenvectors are the multiples of  .
.
Consider the following statements.
(I) P does not have an inverse
(II) P has a repeated eigenvalue
(III) P cannot be diagonalized
Which one of the following options is correct? (2018)
(a) Only I and III are necessarily true
(b) Only II is necessarily true
(c) Only I and II are necessarily true
(d) Only II and III are necessarily true
Ans: (d)
Sol: Theorem: Suppose the n × n matrix A has n linearly independent eigenvectors. If these eigenvectors are the columns of a matrix S, then S−1AS is a diagonal matrix Λ. The eigenvalues of A are on the diagonal of Λ.
S−1AS = Λ (A diagonal Matrix with diagonal values representing eigen values of A) =  Now if A is diagonalizable, S−1 must exist. What is S? S is a matrix whose columns are eigen-vectors of matrix A.
Now if A is diagonalizable, S−1 must exist. What is S? S is a matrix whose columns are eigen-vectors of matrix A.
Now S−1 would only exist if S is invertible. And S would be invertible if all rows and columns of S are independent.
If we would have same eigen-vectors, then S−1 won't exist and hence A won't be diagonalizable.
Even if a matrix A has same eigen values, it does not mean that it is not diagonizable. Take the trivial example of the Identity Matrix I. The Eigen values are 1, 1, 1 and Eigen vectors are
The Eigen values are 1, 1, 1 and Eigen vectors are 
 We form
We form  and this is invertible.
and this is invertible.
So, this makes S−1IS as I = Λ which is in-fact a diagonal matrix.
So, even if we have same eigenvalues the matrix may or may not be diagonalizable. But yes, we need full n set of linearly independent eigenvectors for this matrix A of size n×n to be diagonalizable.
Now our problem says that we have a matrix P whose only eigenvectors are multiples of  Means we have only
Means we have only  as independent eigen vector. Surely, this matrix is not diagonalizable.
as independent eigen vector. Surely, this matrix is not diagonalizable.
Since, eigen vectors are multiples of we have repeated eigen values.
we have repeated eigen values.
Let us assume λ1 and λ2 are different eigen values.
Since, we have only eigen vectors multiple of .
.
Let this vector be x1.
So, Px1 = λ1x1
⟹ Px1 = λ2x1
⟹ λ1x1 = λ2x1
Multiply by x1−1 we get λ1 = λ2. Means, same Eigen vector gives same Eigen Value.
So yes, P has repeated Eigen Values. (II) statement is true.
Now Statement (I) is not true. We cannot say this statement with exact surety.
Consider a matrix  It's eigenvales are λ1 = λ2 = 0.
It's eigenvales are λ1 = λ2 = 0.
All the eigenvectors of this A are multiples of vector (1, 0) or x =
or x =  This matrix surely is not diagonalizable but this matrix A has determinant = 0.
This matrix surely is not diagonalizable but this matrix A has determinant = 0.
Since determinant is 0, so A−1 Doesn't exists.
Hence, (II) and (III) are surely valid under all cases of this question.
For (I) part, Matrix P will not have an inverse when det(P) = 0 and this implies one of the eigenvalue of P is zero. But in question, no where it is mentioned about what are the eigen values. So, I is not necessarily true.
Answer-(D) (Remember options says "necessarily true")
Q17: Consider a matrix  Note that vT denotes the transpose of v. The largest eigenvalue of A is _____. (2018)
Note that vT denotes the transpose of v. The largest eigenvalue of A is _____. (2018)
(a) 3
(b) 2
(c) 1
(d) 4
Ans: (a)
Sol: 
 So, maximum is 3.
So, maximum is 3.
Q18: If A is a skew symmetric matrix then At is (2017)
(a) Diagonal matrix
(b) A
(c) 0
(d) -A
Ans: (d)
Sol: For symmetric matrix, the condition : At = A where t= transpose of matrix
For skew Symmetric matrix , the condition : At = -A
So i think option D will be answer.
Q19: If the characteristics polynomial of 3 x 3 matrix M over R ( the set of real numbers) is λ3 − 4λ2 + aλ + 30, a ∈ R, and one eigenvalue of M is 2, then the largest among the absolute values of the eigenvalues of M is ________. (2017 SET-2)
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (d)
Sol: Given that λ = 2 is an eigen value. So, it must satisfy characterstic equation.
23−4∗22+2a+30 = 0 ⇒ a = −11
Characterstic eq : λ3 − 4λ2 − 11λ + 30
⇒ (λ−2)(λ−5)(λ+3) = 0
λ1 = 2, λ2 = 5 and λ3 = −3
Max Eigen Value = 5
Q20: Consider a quadratic equation x2 − 13x + 36 = 0 with coefficients in a base b. The solutions of this equation in the same base b are x = 5 and x = 6. Then b = ___________. (2017 SET-2)
(a) 4
(b) 6
(c) 8
(d) 9
Ans: (c)
Sol: Let ax2 + bx + c = 0 be a quadratic equation, then
Sum of roots = −b/a and product of roots = c/a
(5)b+(6)b = (13)b ⇒ b = 8
and (5)b∗(6)b = (36)b means 30 = 3b + 6. So, b = 8.
Q21: Let  be two matrices. Then the rank of P +Q is ________. (2017 SET-2)
be two matrices. Then the rank of P +Q is ________. (2017 SET-2)
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (c)
Sol:  det(P+Q) = 0, So Rank cannot be 3, but there exists a 2∗2 submatrix such that determinant of submatrix is not 0.
det(P+Q) = 0, So Rank cannot be 3, but there exists a 2∗2 submatrix such that determinant of submatrix is not 0.
So, Rank (P + Q) = 2.
Q22: Let A be nxn real valued square symmetric matrix of rank 2 with  Consider the following statements.
Consider the following statements.
(I) One eigen value must be in [-5, 5]
(II) The eigen value with the largest magnitude must be strictly greater than 5.
Which of the above statements about eigen values of A is/are necessarily CORRECT? (2017 SET-1)
(a) Both (I) and (II)
(b) (I) only
(c) (II) only
(d) Neither (I) nor (II)
Ans: (b)
Sol: Eigen values of  are ±5. Therefore second statement is false.
are ±5. Therefore second statement is false.
Since, the rank of matrix A is 2, therefore atleast one eigen value would be zero for n ≥ 3.
For n = 2, It can be proven that 
 Both λ1 and λ2 would be real because A is a real symmetric matrix. Which implies that atleast one eigen value would be in [−5, 5].
Both λ1 and λ2 would be real because A is a real symmetric matrix. Which implies that atleast one eigen value would be in [−5, 5].
Hence, correct answer is (B)
Now, to prove  matrix, let us consider the matrix is
matrix, let us consider the matrix is  and λ is the eigen value of this matrix.
and λ is the eigen value of this matrix. Let λ1 and λ2 are roots of this equation.
Let λ1 and λ2 are roots of this equation. = (a + d)2 - 2(ad - bc)
= (a + d)2 - 2(ad - bc) For real valued matrix,
For real valued matrix, (For real symmetric matrix, b = c and ≤ would be replaced by equal sign).
(For real symmetric matrix, b = c and ≤ would be replaced by equal sign).
Q23: Let c1....cn be scalars, not all zero, such that  where ai are column vectors in Rn. Consider the set of linear equations Ax = b
where ai are column vectors in Rn. Consider the set of linear equations Ax = b
where A = a1....an and b =  The set of equations has (2017 SET-1)
The set of equations has (2017 SET-1)
(a) a unique solution at x = Jn where Jn denotes a n-dimensional vector of all 1
(b) no solution
(c) infinitely many solutions
(d) finitely many solutions
Ans: (c)
Sol: Let c1.....cn be scalars, not all zero, such that  where ai are column vectors in Rn.
where ai are column vectors in Rn.
Consider the set of linear equations
Ax = b
where A = [a1.....an] and  The set of equations has
The set of equations has
- a unique solution at x = Jn where Jn denotes a n-dimensional vector of all 1.
- no solution
- infinitely many solutions
- finitely many solutions
Q24: Suppose that the eigen values of matrix A are 1, 2, 4. The determinant of (A−1)T is _________. (2016 SET-2 )
(a) 0
(b) 0.125
(c) 0.25
(d) 0.75
Ans: (b)
Sol: Determinant of Matrix A = product of eigen values = 1×2×4 = 8
Determinant of Inverse Matrix of  Determinant remains same after the Transpose operation.
Determinant remains same after the Transpose operation.
So, determinant of (A-1)T = det(A-1) = 1/8 = 0.125
Q25: Consider the systems,each consisting of m linear equations in n variables.
I. If m < n, then all such systems have a solution
II. If m > n, then none of these systems has a solution
III. If m = n, then there exists a system which has a solution
Which one of the following is CORRECT? (2016 SET-2)
(a) I, II and III are true
(b) Only II and III are true
(c) Only III is true
(d) None of them is true
Ans: (c)
Q26: The coefficient of x12 in (x3 + x4 + x5 + x6 +...)3 is ______. (2016 SET-1)
(a) 6
(b) 10
(c) 12
(d) 16
Ans: (b)
Sol: we will get x12 as
- (x4)3 having coefficient 3C0 = 1
- (x3)2(x6) having coefficient 3C1 = 3
- (x3)(x4)(x5) having coefficient 3C2×2C1 = 6
So it is 10
Second Method:

Q27: Two eigen values of a 3x3 real matrix P are  and 3.The determinantof P is __________. (2016 SET-1)
and 3.The determinantof P is __________. (2016 SET-1)
(a) 9
(b) 15
(c) 6
(d) 30
Ans: (b)
Sol: Eigen values are roots of Characteristic equation |A−λI| = 0.
For a 3 × 3 matrix, characteristic equation will be cubic, so will have 3 roots. Two roots are given as: 2 + i and 3 and We know that complex roots always occur in pairs so, if 2+i is a root of characteristic equation, then 2−i must be other root.
λ1 = 2+i, λ2 = 2−i and λ3 = 3
det(A) = λ1λ2λ3 = (2+i)∗(2−i)∗3 = (22−i2)∗3 = 5 ∗ 3 = 15
Q28: If the following system has non-trivial solution,
px + qy + rz = 0
qx + ry + pz = 0
rx + py + qz = 0,
then which one of the following options is TRUE? (2015 SET-3)
(a) p-q+r = 0 or p = q = -r
(b) p+q-r = 0 or p = -q = r
(c) p+q+r = 0 or p = q = r
(d) p-q+r = 0 or p = -q = -r
Ans: (c)
Sol: for non-trivial solution
|A| = 0
where = prq − p3 − q3 + prq + prq − r3
= prq − p3 − q3 + prq + prq − r3
= 3prq − p3 − q3 − r3
= −(p + q + r)3 + 3(p + q + r)(pq + qr + pr)
now if you check the options the only options where each individual condition can make |A| = 0 zero is C.
Q29: In the given matrix  one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 are (2015 SET-3)
one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 are (2015 SET-3)
(a)  (b)
(b)  (c)
(c)  (d)
(d)  Ans: (b)
Ans: (b)
Sol: 
- -y + 2z = 0
- x + 2y = 0
Now consider each of the triplets as the value of x, y, z and put in these equations the one which satisfies is the answer.
Why so because an eigen vector represents a vector which passes through all the points which can solve these equations.
So, we can observe that only option B is satisfying the equations.
Q30: Perform the following operations on the matrix  (i) Add the third row to the second row
(i) Add the third row to the second row
(ii) Subtract the third column from the first column.
The determinant of the resultant matrix is _____. (2015 SET-2)
(a) 0
(b) 9
(c) 6
(d) 8
Ans: (a)
Sol: Answer 0, because it is easy to see that first column and third column are multiple of each other.
Third column = First column ∗15.
So rank is <3, so Determinant must be 0.
It stays zero as row & column transformations don't affect determinant.
Q31: The larger of the two eigenvalues of the matrix  is _______. (2015 SET-2)
is _______. (2015 SET-2)
(a) 4
(b) 6
(c) 8
(d) 10
Ans: (b)
Sol: For finding the Eigen Values of a Matrix we need to build the Characteristic equation which is of the form,
A − λI
where A is the given Matrix, λ is a constant, I is the identity matrix.
We'll have a Linear equation after solving A − λI, which will give us two roots for λ.
(4−λ)(1−λ)−10 = 0
⇒ 4 - 5λ + λ2 = 10
⇒ λ2 - 5λ - 6 = 0
⇒ (λ - 6)(λ + 1) = 0
⇒ λ = -1, 6.
Q32: Consider the following 2 x 2 matrix A where two elements are unknown and are marked by a and b. The eigenvalues of this matrix are -1 and 7. What are the values of a and b? (2015 SET-1) (a) a = 6, b = 4
(a) a = 6, b = 4
(b) a = 4, b = 6
(c) a = 3, b = 5
(d) a = 5, b =3
Ans: (d)
Sol: Sum of Eigenvalues = Trace of matrix
⇒ −1 + 7 = 1 + a
Product of Eigenvalues = Determinant of matrix
⇒ −1 × 7 = a − 4b
This gives a = 5 and b = 3
Answer = option D.
Q33: In the LU decomposition of the matrix  if the diagonal elements of U are both 1, then the lower diagonal entry l22 of L is________. (2015 SET-1)
if the diagonal elements of U are both 1, then the lower diagonal entry l22 of L is________. (2015 SET-1)
(a) 1
(b) 4
(c) 5
(d) 6
Ans: (c)
Sol: Given,

 l11 = 2
l11 = 2
l11 x u12 = 2
Solving, u12 = 1
l21 = 4
l21 × u12 + l22 = 9
Solving, l22 = 5
Q34: The rank of the matrix  is ____ . (2014)
is ____ . (2014)
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (c)
Sol: Rank of Matrix is 2. Eliminate elements in the 1st column under the 1st element
Eliminate elements in the 1st column under the 1st element Eliminate elements in the 2nd column under the 2nd element
Eliminate elements in the 2nd column under the 2nd element Calculate the number of linearly independent rows
Calculate the number of linearly independent rows That's 2.
That's 2.
Q35: Let A be a square matrix size n x n. Consider the following pseudocode. What is the expected output? (2014 SET-3) (a) The matrix A itself
(a) The matrix A itself
(b) Transpose of the matrix A
(c) Adding 100 to the upper diagonal elements and subtracting 100 from lower diagonal elements of A
(d) None of these
Ans: (a)
Sol: In the computation of given pseudo code for each row and column of Matrix A, each upper triangular element will be interchanged by its mirror image in the lower triangular and after that the same lower triangular element will be again re-interchanged by its mirror image in the upper triangular, resulting the final computed Matrix A same as input Matrix A.
Q36: If V1 and V2 are 4-dimensional subspaces of a 6-dimensional vector space V, then the smallest possible dimension of V1 ∩ V2 is _______. (2014 SET-3)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
Sol: A 6-dimensional vector space {a1, a2, a3, a4, a5, a6}
Let V1 be {a1, a2, a3, a4} and V2 be {a3, a4, a5, a6}
V1 ∩ V2 = {a3, a4}
This is the smallest possible dimension, which is 2.
The largest possible dimension will be 4, when V1 = V2
Q37: Which one of the following statements is TRUE about every n x n matrix with only real eigenvalues? (2014 SET-3)
(a) If the trace of the matrix is positive and the determinant of the matrix is negative, at least one of its eigenvalues is negative.
(b) If the trace of the matrix is positive, all its eigenvalues are positive.
(c) If the determinant of the matrix is positive, all its eigenvalues are positive.
(d) If the product of the trace and determinant of the matrix is positive, all its eigenvalues are positive.
Ans: (a)
Sol: Trace is the sum of all diagonal elements of a square matrix.
Determinant of a matrix = Product of eigen values.
(A) Is the right answer. To have the determinant negative, at least one eigen value has to be negative (but reverse may not be true).
We can take simple example with upper or lower triangular matrices. For options (b), (c) and (d) reverse is always true.
Q38: The product of the non-zero eigenvalues of the matrix is_______. (2014 SET-2)
is_______. (2014 SET-2)
(a) 6
(b) 3
(c) 2
(d) 8
Ans: (a)
Sol: We can see that the rank of the given matrix is 2 (since 3 rows are same, and other 2 rows are also same). Sum of eigen values = sum of diagonals. So, we have two eigen values which sum to 5. This information can be used to get answer in between the following solution.
Let the eigen value be X. Now, equating the determinant of the following to 0 gives us the values for X. To find X in the following matrix, we can equate the determinant to 0. For finding the determinant we can use row and column additions and make the matrix a triangular one. Then determinant will just be the product of the diagonals which should equate to 0.
 Taking X out from R4, 2 − X from R1, (so, X = 2 is one eigen value)
Taking X out from R4, 2 − X from R1, (so, X = 2 is one eigen value)

 Taking X out from R2
Taking X out from R2 R3 ← R3 + R2
R3 ← R3 + R2 Now, we got a triangular matrix and determinant of a triangular matrix is product of the diagonal.
Now, we got a triangular matrix and determinant of a triangular matrix is product of the diagonal.
So, (3 − X)(−X) = 0 ⇒ X = 3 or X = 0. So, X = 3 is another eigen value and product of non-zero eigen values = 2 × 3 = 6.
Q39: A non-zero polynomial f(x) of degree 3 has roots at x = 1,x = 2 and x = 3. Which one of the following must be TRUE? (2014 SET-2)
(a) f(0) f(4) < 0
(b) f(0) f(4) > 0
(c) f(0) + f(4) > 0
(d) f(0) + f(4) < 0
Ans: (a)
Sol: The roots are x = 1, x = 2, and x = 3.
So, polynomial is f(x) = (x − 1)(x − 2)(x − 3)
f(0) = −6, f(4) = 6
So, f(0) f(4) < 0.
Correct Answer: A.
Q40: If the matrix A is such that Then the determinant of A is equal to ________. (2014 SET-2)
Then the determinant of A is equal to ________. (2014 SET-2)
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (a)
Sol: For these kind of matrices Determinant is zero.
A will be a 3 × 3 matrix where the first row will be 2[1 9 5], second row will be −4[1 9 5] and third will be 7[1 9 5]. That is, all the rows of A are linearly dependent which means A is singular.
When matrix is singular |A| = 0.
Q41: A function f(x) is continuous in the interval [0,2]. It is known that f(0)=f(2)=-1 and f(1)=1. Which one of the following statements must be true? (2014 SET-1)
(a) There exists a y in the interval (0, 1) such that f(y) = f(y+1)
(b) For every y in the interval (0,1), f(y) = f(2-y)
(c) The maximum value of the function in the interval (0.2) is 1
(d) There exists a y in the interval (0,1) such that f(y) = -f(2-y)
Ans: (a)
Sol: Let us define a new function g:
g(y) = f(y) − f(y+1)
Since, function f is continuous in [0, 2], g would be continuous in [0, 1].
g(0) = −2, g(1) = 2
Since, g is continuous and goes from negative to positive value in [0, 1], at some point g would be 0 in (0, 1).
g = 0 ⟹ f(y) = f(y+1) for some y ∈ (0, 1).
Therefore, correct answer would be (A).
Q42: The value of the dot product of the eigenvectors corresponding to any pair of different eigenvalues of a 4-by-4 symmetric positive definite matrix is (2014 SET-1)
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (a)
Sol: Let λ1 and λ2 be two distinct eigenvalues of matrix A and u and v be their corresponding eigenvectors respectively.
We know that an eigenvector X corresponding to an eigenvalue λ of matrix A satisfies
AX = λX
∴ Au = λ1u → (1) and Av = λ2v → (2)
On pre-multiplying eqn (1) with vT, we get (Av)Tu = vTλ1u (since A is a symmetric matrix, we can write AT = A)
(Av)Tu = vTλ1u (since A is a symmetric matrix, we can write AT = A)
But Av = λ2v ... from (2) λ2vTu = λ1vTu (as λ1 is a constant, we can write vTλ1 = λ1vT)
λ2vTu = λ1vTu (as λ1 is a constant, we can write vTλ1 = λ1vT) vTu is nothing but the dot product of the eigenvectors u and v.
vTu is nothing but the dot product of the eigenvectors u and v.
Hence, we can conclude that the eigenvectors corresponding to distinct eigenvalues of a real symmetric matrix are orthogonal.
Q43: Consider the following system of equations:
3x + 2y = 1
4x + 7z = 1
x + y + z = 3
x - 2y + 7z = 0
The number of solutions for this system is (2014 SET-1)
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (b)
Sol: Since, equation (2) - equation (1) produces equation (4), we have 3 independent equations in 3 variables, hence unique solution.
So, answer is 1.
Q44: What is the matrix transformation which takes the independent vectors  and transforms them to
and transforms them to  respectively? (2013)
respectively? (2013)
(a)  (b)
(b)  (c)
(c)  (d)
(d)  Ans: (d)
Ans: (d)
Q45: Which one of the following does NOT equal  (2013)
(2013)
(a)  (b)
(b)  (c)
(c)  (d)
(d)  Ans: (a)
Ans: (a)
Sol: Operations are:
Operations are:
C3 ← C3 + C2
C2 ← C2 + C1
Swap C2 & C3
The Swapping operations make the determinant as (−1) ∗ |A|
whereas the other options have their determinant as |A|.
Q46: Let A be the 2x2 matrix with elements a11 = a12 = a21 = +1 and a22 = −1. Then the eigenvalues of the matrix A19 are (2012)
(a) 1024 and -1024
(b) 1024√2 and -1024√2
(c) 4√2 and -4√2
(d) 512√2 and -512√2
Ans: (d)
Sol: Characteristic Equation is |A - μI| = 0
 According to properties of Eigen values,eigen values of A19 = (eigen value of A)19
According to properties of Eigen values,eigen values of A19 = (eigen value of A)19
= (√2)19 and (−√2)19
Hence, Ans is option (D).
Q47: What is the matrix that represents rotation of an object by θ° about the origin in 2D? (2011)
(a)  (b)
(b)  (c)
(c)  (d)
(d)  Ans: (a)
Ans: (a)
Sol: In rotation, we rotate the object at particular angle θ (theta) from its origin. From the following figure, we can see that the point P(X, Y) is located at angle φ from the horizontal X coordinate with distance r from the origin.
Let us suppose you want to rotate it at the angle θ. After rotating it to a new location, you will get a new point P’ (X’, Y’). Using standard trigonometric the original coordinate of point P(X, Y) can be represented as −
Using standard trigonometric the original coordinate of point P(X, Y) can be represented as −
X = r cosϕ ....(1)
Y = r sinϕ ....(2)
Same way we can represent the point P’ (X’, Y’) as −
X′ = rcos(θ + ϕ) = rcosϕ cosθ − rsinϕ sinθ .....(3)
Y′ = rsin(θ + ϕ) = rcosϕ sinθ + rsinϕ cosθ .....(4)
Substituting equation (1) & (2) in (3) & (4) respectively, we will get
X′ = Xcosθ −Ysinθ
Y′ = Xsinθ + Ycosθ
Representing the above equation in matrix form, P' = P.R
P' = P.R
Where R is the rotation matrix
The rotation angle can be positive and negative.
For positive rotation angle, we can use the above rotation matrix. However, for negative angle rotation, the matrix will change as shown below −
Q48: If A and B are square matrices with same order and A is symmetric, then BTAB is (2011)
(a) Skew symmetric
(b) Symmetric
(c) Orthogonal
(d) Idempotent
Ans: (b)
Sol: If A is a Symmetric Matrix then A = A⊤ // Sign ⊤ Showing as Transpose
(B⊤AB)⊤ = B⊤A⊤B
it is already given A = A⊤ So
B⊤AB
Answer : Symmetric
Q49: Consider the matrix as given below. Which one of the following provides the CORRECT values of eigenvalues of the matrix? (2011)
Which one of the following provides the CORRECT values of eigenvalues of the matrix? (2011)
(a) 1, 4, 3
(b) 3, 7, 3
(c) 7, 3, 2
(d) 1, 2, 3
Ans: (a)
Sol: The given matrix is an upper triangular matrix and the eigenvalues of upper or lower triangular matrix are the diagonal values itself.(Property)
Q50: Consider the following matrix  If the eigenvalues of A are 4 and 8, then (2010)
If the eigenvalues of A are 4 and 8, then (2010)
(a) x = 4, y = 10
(b) x = 5, y = 8
(c) x = -3, y = 9
(d) x = -4, y = 10
Ans: (d)
Sol: Sum of eigenvalues is equal to trace (sum of diagonal elements) and product of eigen values is equal to the determinant of matrix
So, 2+y = 8+4 and 2y−3x = 32
Solving this we get y = 10, x = −4.
Option D is answer.
|
34 videos|115 docs|72 tests
|
FAQs on Previous Year Questions: Linear Algebra - Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE)
| 1. What are the applications of linear algebra in computer science engineering? |  |
| 2. How is linear algebra used in developing algorithms in computer science engineering? |  |
| 3. How does linear algebra help in understanding data structures in computer science engineering? |  |
| 4. Can linear algebra be used for solving optimization problems in computer science engineering? |  |
| 5. How does linear algebra contribute to the field of computer vision in computer science engineering? |  |
|
34 videos|115 docs|72 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|

















