Previous Year Questions : Polynomials | Mathematics (Maths) Class 9 PDF Download
Very short Answer Type Questions
Q1.Classify the following as linear, quadratic, and cubic polynomials:
(i) x2+4
(ii) x−3x2
(iii) 7y3−5y2+4
(iv) 3x+2
(v) 5x2−6x+8
 View Answer
View Answer 
Sol:
(i) x2+4
- Quadratic Polynomial (degree 2)
(ii) 2x−3x2
- Quadratic Polynomial (degree 2)
(iii) 7y3−5y2+4
- Cubic Polynomial (degree 3)
(iv) 3x+2
- Linear Polynomial (degree 1)
(v) 5x2−6x+8
- Quadratic Polynomial (degree 2)
Q2.Find the value of each of the following polynomials at the indicated value of the variables:
(i) p(x)=x3−4x +2 at x=−1.
(ii) q(y)=4y2−3y+7 at y=0
 View Answer
View Answer 
Sol:
(i) Find p(−1):
Substitute x=−1 into the polynomial p(x) = x3−4x+2:
p(−1) = (−1)3−4(−1)+2p(−1) = −1+4+2
p(−1) = 5
(ii) Find q(0):
Substitute y=0 into the polynomial q(y) = 4y2−3y +7:
q(0) = 4(0)2−3(0) +7q(0)=0−0+7
q(0)=7
Q3. What is the value of (x + y)3 – 3xy (x + y)?
 View Answer
View Answer 
Sol:
∵ (x + y)3 = x3 + y3 + 3xy (x + y)
∴ [x3 + y3 + 3xy (x + y)] – [3xy (x + y)] = x3 + y3
⇒ (x + y)3 – 3xy(x + y) = x3 + y3
Thus, value of x3 + y3 is (x + y)3 – 3xy (x + y) = x3 + y3
Q4.Check whether -1 and 3 are zeros of the polynomial x2−2x−3.
 View Answer
View Answer 
Sol:Let p(x)=x2−2x−3.
Now, check the values of the polynomial at x=−1 and x=3:
For x=−1:
p(−1)=(−1)2−2(−1)−3 =1+2−3 =0
So, −1 is a zero of the polynomial.
For x=3:
p(3)=32−2(3)−3 =9−6−3 =0
So, 3 is also a zero of the polynomial.
Conclusion: Both -1 and 3 are zeros of the polynomial x2−2x−3.
Q5. Write the degree of the polynomial 4x4 + 0x3 + 0x5 + 5x + 7?
 View Answer
View Answer 
Sol:The degree of 4x4 + 0x3 + 0x5 + 5x + 7 is 4.
Q6. What is the zero of the polynomial p(x) = 2x + 5?
 View Answer
View Answer 
Sol:∵ p(x) = 0 ⇒ 2x + 5 = 0
⇒ x = -5/2
∴ zero of 2x + 5 is -5/2
Q7. Which of the following is one of the zeros of the polynomial 2x2 + 7x – 4?
 View Answer
View Answer 
Sol:∵ 2x2 + 7x – 4 = 2x2 + 8x – x – 4
⇒ 2x (x + 4) – 1 (x + 4) = 0
⇒ (x + 4) (2x – 1) = 0
⇒ x = – 4, x = 1/2,
∴ One of the zero of 2x2 + 7x – 4 is 1/2.
Q8. Verify whether 1 and -1 are zeros of the polynomial x2+3x−4.
 View Answer
View Answer 
Sol:Let p(x)=x2+3x−4.
For x=1:
p(1)=12+3(1)−4 =1+3−4 =0So, x=1 is a zero of the polynomial.
For x=−1:
p(−1)=(−1)2+3(−1)−4=1−3−4=−6So, x=−1 is not a zero of the polynomial.
Q9.Write the degrees of each of the following polynomials:
(i) 7x3 + 4x2 – 3x + 12
(ii) 12 – x + 2x3
 View Answer
View Answer 
Sol:As we know, degree is the highest power in the polynomial
(i) Degree of the polynomial 7x3 + 4x2 – 3x + 12 is 3
(ii) Degree of the polynomial 12 – x + 2x3 is 3
Q10.State whether the following expression is polynomial or not. In case of a polynomial, write its degree.
x100 - 1
 View Answer
View Answer 
Sol:Given expression is x100−1.
Since all the exponents of x are whole numbers and the highest exponent of x is 100, it is a polynomial of degree 100.
Short Answer Type Questions
Q1.Simplify :(a + b + c)2 + (a − b + c)2
 View Answer
View Answer 
Sol:(a + b + c)2 + (a − b + c)2
= (a2 + b2 + c2 + 2ab+2bc+2ca) + (a2 + (−b)2 + c2 −2ab−2bc+2ca)
= 2a2 + 2 b2 + 2c2 + 4ca
Q2.Factorise the following: 2x2-7x-15
 View Answer
View Answer 
Sol: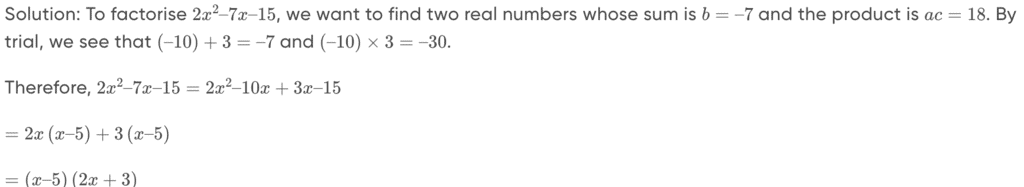
Q3. Factorize x2 – x – 12.
 View Answer
View Answer 
Sol:
We have x2 – x – 12
⇒ x2 – 4x + 3x – 12
⇒ x(x – 4) + 3(x – 4)
⇒ (x – 4)(x + 3)
Thus, x2 – x – 12 = (x – 4)(x + 3)
Q4.Write the following in the expanded form:
(i) (a + 2b + c)2
(ii) (2a − 3b − c)2
 View Answer
View Answer 
Sol:
Using identities:
(x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2xz
(i) (a + 2b + c)2
= a2 + (2b)2 + c2 + 2a(2b) + 2ac + 2(2b)c
= a2 + 4b2 + c2 + 4ab + 2ac + 4bc
(ii) (2a − 3b − c)2
= [(2a) + (−3b) + (−c)]2
= (2a)2 + (−3b)2 + (−c)2 + 2(2a)(−3b) + 2(−3b)(−c) + 2(2a)(−c)
= 4a2 + 9b2 + c2 − 12ab + 6bc − 4ca
Q5. State whether the following expression is a polynomial or not: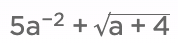
 View Answer
View Answer 
Sol:
A polynomial is an expression consisting of variables and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents.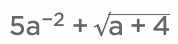 is not a polynomial.
is not a polynomial.
Long Answer Type Questions
Q1. Check whether (x – 1) is a factor of the polynomial x3 – 27x2 + 8x + 18.
 View Answer
View Answer 
Sol:
Here, p(x) = x3 – 27x2 + 8x + 18, (x – 1) will be a factor of p(x) only if (x – 1) divides p(x) leaving a remainder 0.
For x – 1 = 0
⇒ x = 1
∴ p(1) = (1)3 – 27(1)2 + 8(1) + 18
⇒ 1 – 27 + 8 + 18
⇒ 27 – 27
⇒ 0
Since, p(1) = 0
∴ (x – 1) is a factor of p(x).
Thus, (x – 1) is a factor of x3 – 27x2 + 8x + 18.
Q2. (a) For what value of k, the polynomial x2 + (4 – k)x + 2 is divisible by x – 2?
(b) For what value of ‘m’ is x3 – 2mx2 + 16 is divisible by (x + 2)?
 View Answer
View Answer 
Sol:
(a) Here p(x) = x2 + 4x – kx + 2
If p(x) is exactly divisible by x – 2, then p(2) = 0
i.e. (2)2 + 4(2) – k(2) + 2 = 0
⇒ 4 + 8 – 2k + 2 = 0
⇒ 14 – 2k = 0
⇒ 2k = 14
⇒ k= 14/2 = 7
Thus, the required value of k is 7.
(b) Here, p(x) = x3 – 2mx2 + 16
∴ p(–2) = (–2)3 –2(–2)2m + 16
⇒ –8 –8m + 16
⇒ –8m + 8
Since, p(x) is divisible by x + 2
∴ p(–2) = 0
or –8m + 8 = 0
⇒ m = 1
Q3.If f(x) = 2x3 – 13x2 + 17x + 12, find
(i) f (2)
(ii) f (-3)
(iii) f(0)
 View Answer
View Answer 
Sol:f(x) = 2x3 – 13x2 + 17x + 12
(i) f(2) = 2(2)3 – 13(2)2 + 17(2) + 12
= 2 x 8 – 13 x 4 + 17 x 2 + 12
= 16 – 52 + 34 + 12
= 62 – 52
= 10
(ii) f(-3) = 2(-3)3 – 13(-3)2 + 17 x (-3) + 12
= 2 x (-27) – 13 x 9 + 17 x (-3) + 12
= -54 – 117 -51 + 12
= -222 + 12
= -210
(iii) f(0) = 2 x (0)3 – 13(0)2 + 17 x 0 + 12
= 0-0 + 0+ 12
= 12
Q4. Simplify each of the following using identities :
(i) (x + 3)3 + (x – 3)3
(ii) (x/2 + y/3)3 – (x/2 – y/3)3
(iii) (x + 2/x)3 + (x – 2/x)3
 View Answer
View Answer 
Sol:
[Using identities:1. a3 + b3 = (a + b)(a2 + b2 – ab)
2. a3 – b3 = (a – b)(a2 + b2 + ab)
3. (a + b)(a-b) = a2 – b2
4. (a + b)2 = a2 + b2 + 2ab and
5. (a – b)2 = a2 + b2 – 2ab ]
(i) (x + 3)3 + (x – 3)3
Here a = (x + 3), b = (x – 3)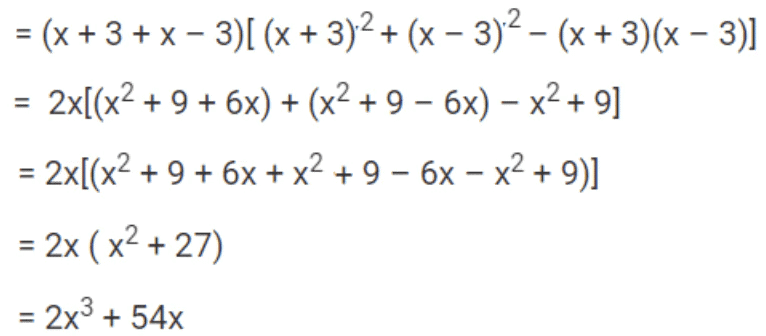 (ii) (x/2 + y/3)3 – (x/2 – y/3)3
(ii) (x/2 + y/3)3 – (x/2 – y/3)3
Here a = (x/2 + y/3) and b = (x/2 – y/3)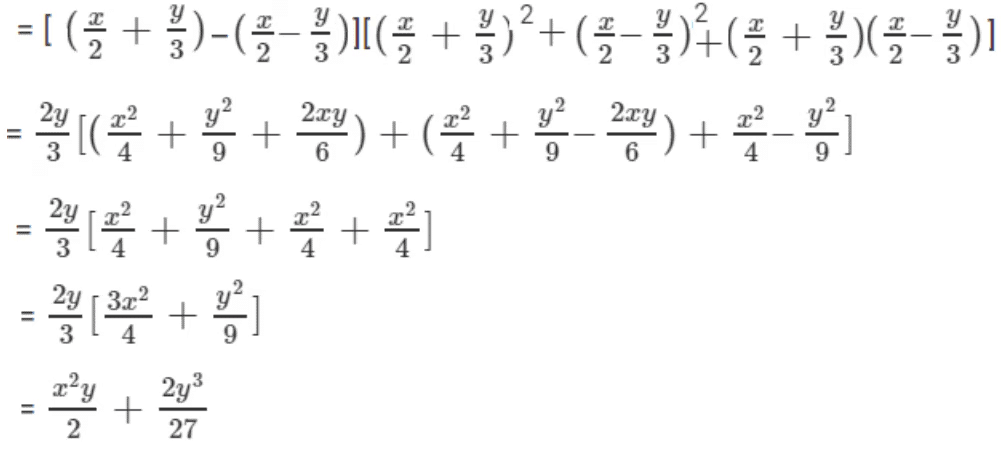
(iii) (x + 2/x)3 + (x – 2/x)3
Here a = (x + 2/x) and b = (x – 2/x)
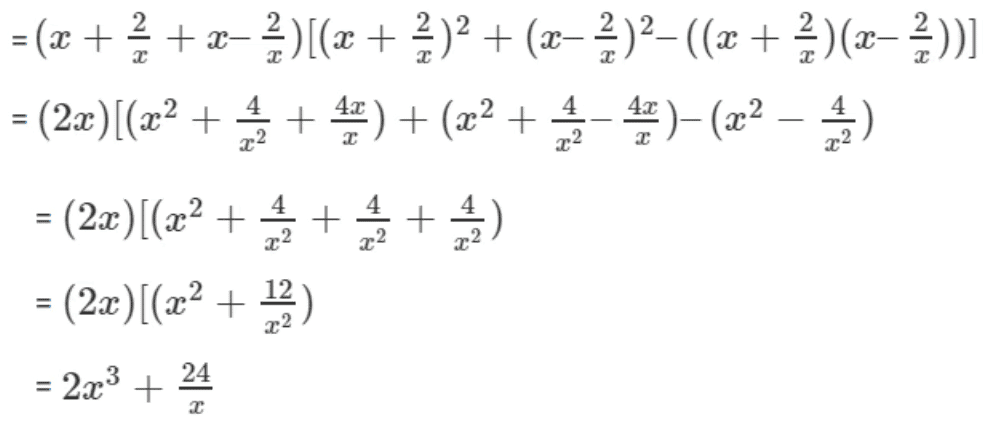
|
40 videos|563 docs|57 tests
|
FAQs on Previous Year Questions : Polynomials - Mathematics (Maths) Class 9
| 1. What are polynomials and how are they classified? |  |
| 2. What are the key properties of polynomials? |  |
| 3. How do you find the roots of a polynomial? |  |
| 4. What is the relationship between the coefficients and the roots of a polynomial? |  |
| 5. Can you explain the Remainder Theorem and its application? |  |

















