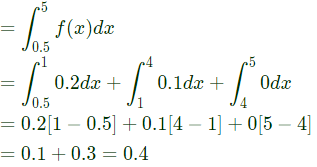Q1: Let X be a discrete random variable that is uniformly distributed over the set {−10, −9, …, 0,…, 9, 10}. Which of the following random variables is/are uniformly distributed? (2024)
(a) X2
(b) X3
(c) (X - 5)2
(d) (X + 10)2
Ans: (b, d)
Sol: 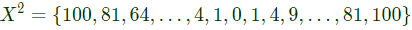
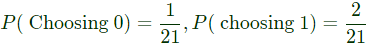 So, X2 is not uniformly distributed.
So, X2 is not uniformly distributed.
(X−5)2 = {225, 199,….4, 1, 0, 1, 4, 9, 16, 25}
Again probability of choosing any number is not equal so (X−5)2 is also not uniformly - distributed.
(X+10)2 = {0, 1, 4, 9, 16,… 81, 100, 121,…. 400}
P (Choosing any number) = 1/21 = so is it uniformly-distributed
Now, X3 = {−1000, − 729, −512,…,−8, −1, 0, 1, 8, … 729, 1000}
Again P (Choosing any number) = 1/21 = Constant
So, it is also uniformly-distributed.
Q2: The expected number of trials for first occurrence of a "head" in a biased coin is known to be 4. The probability of first occurrence of a "head" in the second trial is ___ (Round off to 3 decimal places). (2023)
(a) 0.125
(b) 0.188
(c) 0.254
(d) 0.564
Ans: (b)
Sol: Let probability of head = P
Let probability of Tail = q = P - 1
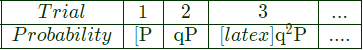 ∴ Expected No. of trail
∴ Expected No. of trail
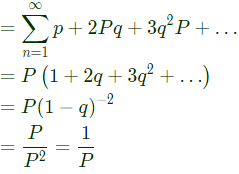 Given : Trial = 4
Given : Trial = 4
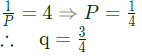 Now, probability of head for second trail.
Now, probability of head for second trail.
= qP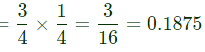
Q3: Let the probability density function of a random variable x be given as
f(x) = ae−2∣x∣
The value of ′a′ is _________ (2022)
(a) 0.5
(b) 1
(c) 1.5
(d) 2
Ans: (b)
Sol: 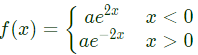 Therefore,
Therefore,
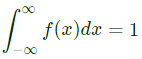
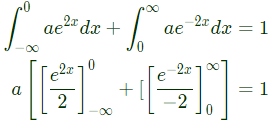
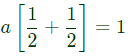 a = 1
a = 1
Q4: Suppose the probability that a coin toss shows "head" is p, where 0 < p < 1. The coin is tossed repeatedly until the first "head" appears. The expected number of tosses required is (2021)
(a) p/(1−p)
(b) (1−p)/p
(c) 1/p
(d) 1/p2
Ans: (c)
Sol: 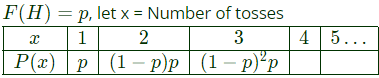
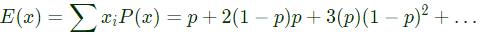
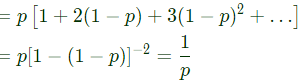
Q5: The probability of a resistor being defective is 0.02. There are 50 such resistors in a circuit. The probability of two or more defective resistors in the circuit (round off to two decimal places)is ________ (2019)
(a) 0.1
(b) 0.26
(c) 0.65
(d) 0.85
Ans: (b)
Sol: 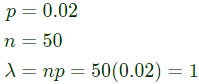
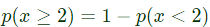
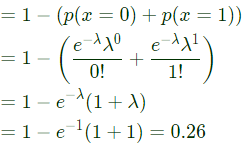
Q6: The mean-square of a zero-mean random process is kT/C, where k is Boltzmann's constant, T is the absolute temperature, and C is a capacitance. The standard deviation of the random process is (2019)
(a) kT/C
(b) 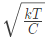
(c) C/KT
(d) 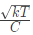
Ans: (b)
Sol: Given that,
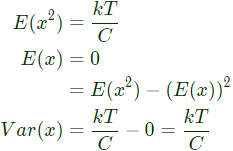 Standard deviation =
Standard deviation = 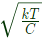
Q7: A person decides to toss a fair coin repeatedly until he gets a head. He will make at most 3 tosses. Let the random variable Y denote the number of heads. The value of var {Y}, where var {.} denotes the variance, equals (SET-2 (2017))
(a) 7/8
(b) 49/64
(c) 7/64
(d) 105/64
Ans: (c)
Sol: 
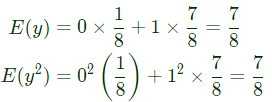
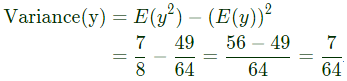
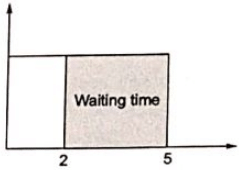
Q8: Assume that in a traffic junction, the cycle of the traffic signal lights is 2 minutes of green (vehicle does not stop) and 3 minutes of red (vehicle stops). Consider that the arrival time of vehicles at the junction is uniformly distributed over 5 minute cycle. The expected waiting time (in minutes) for the vehicle at the junction is ________. (SET-2 (2017))
(a) 0.4
(b) 0.9
(c) 1.5
(d) 2.6
Ans: (b)
Sol: t be arrival time of vehicles of the junction is uniformaly distributed in [0, 5].
Let y be the waiting time of the junction.
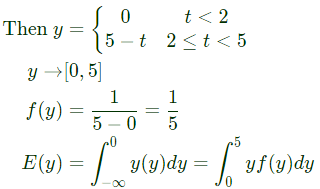
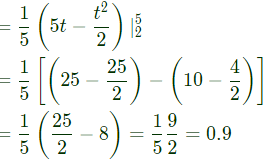
Q9: An urn contains 5 red balls and 5 black balls. In the first draw, one ball is picked at random and discarded without noticing its colour. The probability to get a red ball in the second draw is (SET-2 (2017))
(a) 1/2
(b) 4/9
(c) 5/9
(d) 6/9
Ans: (a)
Sol: 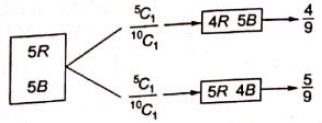
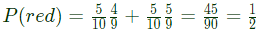
Q10: Let the probability density function of a random variable, X, be given as: 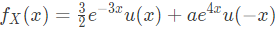 where u(x) is the unit step function.
where u(x) is the unit step function.
Then the value of 'a' and Prob{X ≤ 0}, respectively, are (SET-2 (2016))
(a) 2, 1/2
(b) 4, 1/2
(c) 2, 1/4
(d) 4, 1/4
Ans: (a)
Sol: 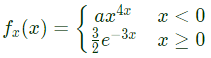
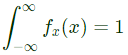
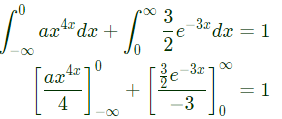
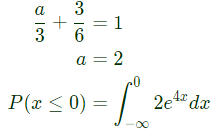
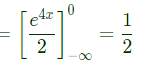
Q11: Candidates were asked to come to an interview with 3 pens each. Black, blue, green and red were the permitted pen colours that the candidate could bring. The probability that a candidate comes with all 3 pens having the same colour is _____. (SET-1(2016))
(a) 0.1
(b) 0.2
(c) 0.4
(d) 0.8
Ans: (b)
Q12: Two players, A and B, alternately keep rolling a fair dice. The person to get a six first wins the game. Given that player A starts the game, the probability that A wins the game is (SET-1(2015))
(a) 5/11
(b) 1/2
(c) 7/13
(d) 6/11
Ans: (d)
Sol: P(A wins) = P( 6 in first throw by A) + P(A not 6, B not 6,) + ...
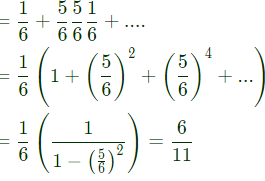
Q13: A random variable X has probability density function f(x) as given below:
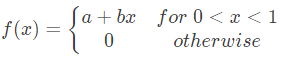 If the expected value E[X] = 2/3, then Pr[X < 0.5] is ______. (SET-1(2015))
If the expected value E[X] = 2/3, then Pr[X < 0.5] is ______. (SET-1(2015))
(a) 0.25
(b) 0.5
(c) 0.75
(d) 1
Ans: (a)
Sol: 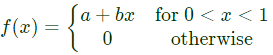
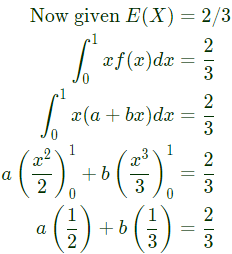
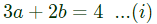
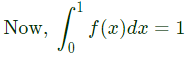
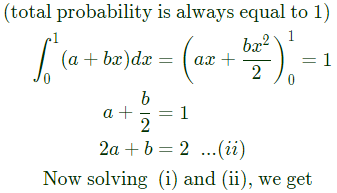
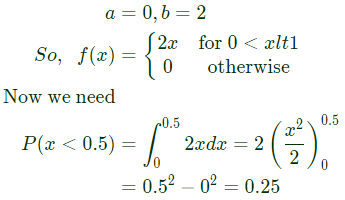
Q14: Lifetime of an electric bulb is a random variable with density f(x) = kx2, where x is measured in years. If the minimum and maximum lifetimes of bulb are 1 and 2 years respectively, then the value of k is _____ (SET-3 (2014))
(a) 0.85
(b) 0.42
(c) 0.25
(d) 0.75
Ans: (b)
Sol: Life time of an electric bulb with density
 If minimum and maximum lifetimes of bulb are 1 and 2 years respectively then
If minimum and maximum lifetimes of bulb are 1 and 2 years respectively then
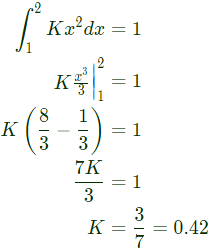
Q15: Let X be a random variable with probability density function 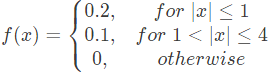 The probability P(0.5 < X < 5) is (SET-2 (2014))
The probability P(0.5 < X < 5) is (SET-2 (2014))
(a) 0.15
(b) 0.40
(c) 0.75
(d) 0.85
Ans: (b)
Sol: Probability (0.5 < n < 5)
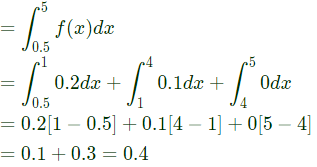
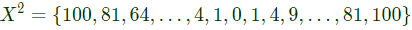
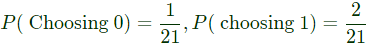 So, X2 is not uniformly distributed.
So, X2 is not uniformly distributed.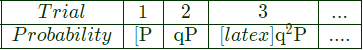 ∴ Expected No. of trail
∴ Expected No. of trail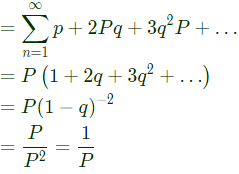 Given : Trial = 4
Given : Trial = 4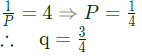 Now, probability of head for second trail.
Now, probability of head for second trail.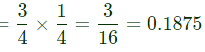
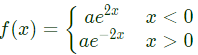 Therefore,
Therefore,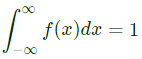
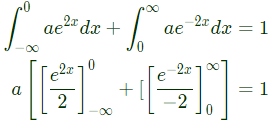
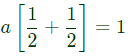 a = 1
a = 1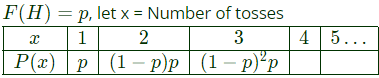
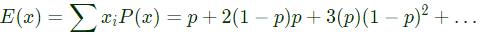
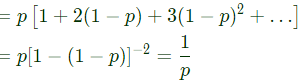
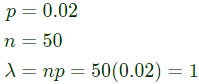
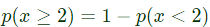
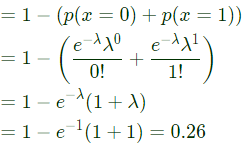
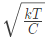
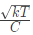
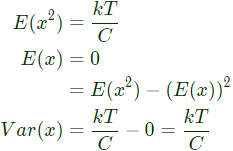 Standard deviation =
Standard deviation = 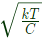

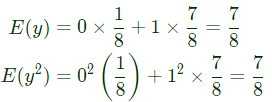
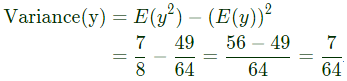

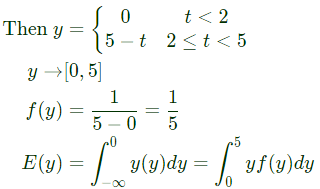
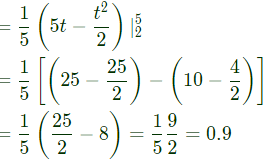

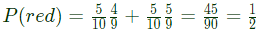
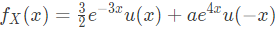 where u(x) is the unit step function.
where u(x) is the unit step function.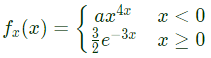
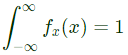
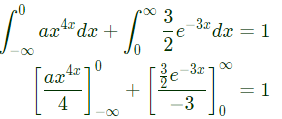
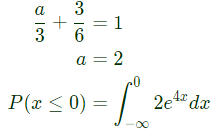
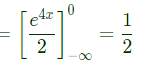
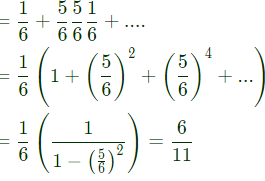
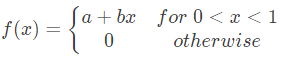 If the expected value E[X] = 2/3, then Pr[X < 0.5] is ______. (SET-1(2015))
If the expected value E[X] = 2/3, then Pr[X < 0.5] is ______. (SET-1(2015))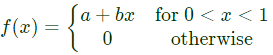
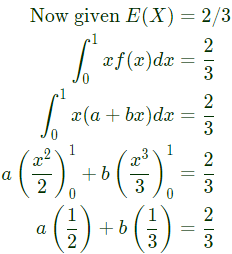
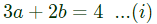
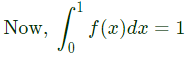
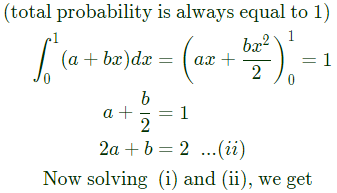
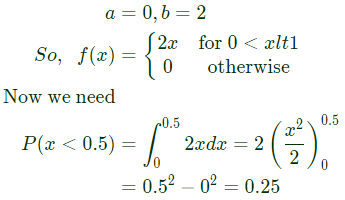
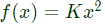 If minimum and maximum lifetimes of bulb are 1 and 2 years respectively then
If minimum and maximum lifetimes of bulb are 1 and 2 years respectively then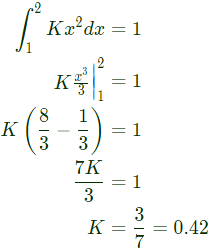
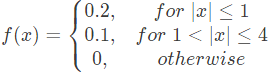 The probability P(0.5 < X < 5) is (SET-2 (2014))
The probability P(0.5 < X < 5) is (SET-2 (2014))