Previous Year Questions: Propositional Logic | Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE) PDF Download
Q1: Let p and q be the following propositions:
p : Fail grade can be given.
q : Student scores more than 50% marks.
Consider the statement: "Fail grade cannot be given when student scores more than 50% marks."
Which one of the following is the CORRECT representation of the above statement in propositional logic? (2024 SET-2)
(a) q → ¬p
(b) q → p
(c) p → q
(d) ¬p → q
Ans: (a)
Sol: Q when P means P→Q.
Given statement,
P : Fail grade can be given.
Q : Student score more than 50% marks.
¬P : Fail grade cannot be given
So,
Fail grade cannot be given when student score more than 50% marks.
is written as Q→¬P
Correct answer is option A.
Q2: Geetha has a conjecture about integers, which is of the form
∀x [P(x) ⇒ ∃yQ(x, y)]
where P is a statement about integers, and Q is a statement about pairs of integers. Which of the following (one or more) option(s) would imply Geetha's conjecture? (2023)
(a) ∃x [P(x) ∧ ∀yQ (x, y)]
(b) ∀x ∀yQ (x, y)
(c) ∃y ∀x [P(x) ⇒ Q(x, y)]
(d) ∃x [P(x) ∧ ∃yQ (x, y)]
Ans: (b, c)
Sol: Here, domain is the set of integers, So, elements x, y∈{...,−3, −2, −1, 0, 1, 2, 3,...} and assuming a tautology is defined as a formula or assertion that is true in every possible interpretation.
Since, statement ∀x P(x) is same as P(1) ∧ P(2) ∧... and statement ∃xP(x) is same as P(1) ∨ P(2)∨...
(Here, “...” contains all the elements from the domain, not only positive integers) and A implies B is true means A ⇒ B is a tautology. Some points can be noted as:
- Symbols ∀(universal quantifier) is used for conjunction and ∃ (existential quantifier) is used for disjunction.
- ¬∀x¬ ≡ ∃x and ¬∃x¬ ≡ ∀x
- Using Null Quantification, we can write ∀x (P(x) ⇒ ∃yQ (x, y)) as ∀x∃y(P(x) ⇒ Q(x, y)). Both are equivalent expressions.
Method 1:
B. ∀x ∀yQ(x, y) ⇒ [∀x (P(x) ⇒ ∃yQ(x, y))]
≡ ∀x ∀yQ(x, y) ⇒ [∀x ∃y(P(x) ⇒ Q(x, y))]
≡ ∀x ∀yQ(x, y) ⇒ [∀x ∃y(¬P(x) ∨ Q(x, y))]
≡ ∀x ∀yQ(x, y) ⇒ [∀x(¬∀y(P(x) ∧ ¬Q(x, y))]
Now, both sides of ⇒ there are ∀ (universal) quantifier and which is used for conjunction. If we try to make left side true then right side should also be true to become this formula as tautology.
So, left side is true when Q(x, y) is true for each x, y from the domain and so in right side, ¬Q(x, y) becomes false and so, P(x) ∧ ¬Q(x, y) becomes false and so, ¬∀y(P(x) ∧ ¬Q(x, y) becomes true and so, ∀x(¬∀y(P(x) ∧ ¬Q(x, y)) becomes true.
Hence, when left side is true then right sides is also true and so, it is a tautology and so, B is correct.
C. ∃y∀x (P(x) ⇒ Q(x, y)) ⇒ [∀x(P(x) ⇒ ∃yQ(x, y))]
≡ ∃y∀x(P(x) ⇒ Q(x, y)) ⇒ [∀x∃y(P(x) ⇒ Q(x, y))]
≡ ∃y∀xR(x, y) ⇒ ∀x∃yR(x, y)
Now, Consider the interpretation of R(x, y) as x + y = 0. Now, ∃y∀xR(x, y) means that “There exist an integer y such that for every ineger x, R(x, y)” which is false because if we choose any y then there will be “only one” x. In the same way, ∀x∃yR(x, y) is true because for every x there exist a y such that x + y = 0.
∃y∀xR(x, y) is true if and only if there exist a y which makes R(x, y) true for every x. So, y does not depend on x.
∀x∃yR(x, y) is true if and only if there exist a y which makes R(x, y) true for every x. So, y does not depend on x.
So, ∃y∀xR(x, y) is stronger than ∀x∃yR(x, y).
Hence, if ∃y∀xR(x, y) is true then ∀x∃yR(x, y) must also be true but if ∀x∃yR(x, y) is true then ∃y∀xR(x, y) need not be true as can be seen from above interpretation of x + y = 0.
A. ∃x(P(x) ∧ ∀yQ(x, y)) ⇒ [∀x(P(x) ⇒ ∃yQ(x, y))]
≡ ¬∀x[P(x) ⇒ ∃y¬Q(x, y)] ⇒ [∀x(P(x)⇒ ∃yQ(x, y))]
≡ ¬[P(1) ⇒ ∃y ¬ Q(1, y) ∧ P(2) ⇒ ∃y ¬ Q(2, y) ∧...]
⇒ [P(1) ⇒ ∃yQ(1, y) ∧ P(2) ⇒ ∃yQ(2, y)∧...]
Now, assign P(1) and P(2) as True and Q(1, y) is False for every y and Q(2, y) is True for every y which makes right side of ⇒ as False and left side as True. Hence, it is not a tautology.
D. ∃x(P(x) ∧ ∃yQ(x, y)) ⇒ [∀x(P(x) ⇒ ∃yQ(x, y))]
≡ ¬∀x[P(x) ⇒ ∀y¬Q(x, y)] ⇒ [∀x(P(x) ⇒ ∃yQ(x, y))]
≡ ¬[P(1) ⇒ ∀y¬Q(1, y) ∧ P(2) ⇒ ∀y¬Q(2, y) ∧...]
⇒ [P(1) ⇒ ∃yQ(1, y) ∧ P(2) ⇒ ∃yQ(2, y) ∧...]
Now, assign P(1) and P(2) as True and Q(1, y) is False for every y and Q(2, y) is True for every y which makes right side of ⇒ as False and left side as True. Hence, it is not a tautology.
Hence, B and C are correct options.
Method 2 :
We can write the given conjecture as:
S: [P(1) ⇒ (Q(1, 1) ∨ Q(1, 2) ∨...)] ∧ [P(2) ⇒ (Q(2, 1) ∨ Q(2, 2) ∨...)] ∧...
Now, A implies B is true means A ⇒ B is a tautology.
So, here, we will try to make above statement S as False and try to make each given option as True and if we are able to do it, then it will not be a tautology and hence, that option does not imply S.
Now, if we try to make S as False, it means at least one [P(x) ⇒ ∃yQ(x, y)] is False which means:
The conditions are:
(1) P(a) is True for at least one a and
(2) Q(a, b) is False for all y with the corresponding a from (1).
Where a and b come from the domain.
Now, comes to each option one by one.
(A) We can write it as:
[P(1) ∧ ∀yQ(1, y)] ∨ [P(2) ∧ ∀yQ (2, y)]∨...
We can make it as true by making P(1) as true and ∀yQ(1, y) as false to satisfy the above conditions and for other P(c) as true and ∀yQ(c, y) as True where c ≠ 1. In this way, above condition is also satisfied and also, we are able to make whole statement true.
Hence, (A) is wrong.
(B) We can write it as:
∀yQ(1, y) ∧ ∀yQ(2, y)∧...
Now, we can't make it as true because according to the above condition (2), Q(a, b) is False for all b with at least one a which makes whole statement false.
Hence, (B) is correct.
(C) We can write it as:
∃y[(P(1) ⇒ Q(1, y)) ∧ (P(2) ⇒ Q(2, y)) ∧ ...]
Again, we can't make it True because we can set P(1) as True and Q(1, y) as False for all y. In this way above condition is satisfied and also the whole statement becomes False.
Hence, (C) is correct.
(D) We can write it as:
[P(1) ∧ ∃yQ (1, y)] ∨ [P(2) ∧ ∃yQ(2, y)]∨...]
We can make this statement as true by making P(1) as true and ∃yQ(1, y) as False which satisfies the given condition but we can make P(2) as true and ∃yQ(2, y) as True and in this way, whole statement becomes true.
Hence, (D) is wrong.
Q3: The number of arrangements of six identical balls in three identical bins is ____. (2022)
(a) 7
(b) 8
(c) 12
(d) 5
Ans: (a)
Sol: This is “indistinguishable objects into indistinguishable boxes(IOIB)” problem which is a standard combinatorial problem. There is no simple closed formula for the number of ways to distribute n indistinguishable objects into j indistinguishable boxes.
So, We will enumerate all the ways to distribute.
Best way is to go in a sequence, covering all possibilities, So, that we do not overcount, we do not undercount.
Case 1 : If only one bin is used :
(6,0,0) i.e. Only 1 way (Since All balls have to be put in this single bin that is used ; Since all bins are identical, so, it doesn’t matter which bin we use)
Case 2 : If two bins are used :
The distribution can be done as any of the following :
(5,1) (which means 5 identical balls in one bin, 1 ball in another bin, and the third bin is unused)
(4,2) (which means 4 identical balls in one bin, 2 balls in another bin, and the third bin is unused)
(3,3) (which means 3 identical balls in one bin, 3 balls in another bin, and the third bin is unused)
i.e. 3 ways to distribute 6 identical balls into 3 identical bins if exactly two of the bins are used.
Case 3 : If three bins are used :
The distribution can be done as any of the following :
(4,1,1) (which means 4 identical balls in one bin, 1 ball in another bin, and 1 ball in the third bin)
(3,2,1) (which means 3 identical balls in one bin, 2 ball in another bin, and 1 ball in the third bin)
(2,2,2) (which means 2 identical balls in one bin, 2 ball in another bin, and 2 ball in the third bin)
i.e. 3 ways to distribute 6 identical balls into 3 identical bins if all three of the bins are used.
So, total we have 7 ways to distribute 6 identical balls in 3 identical bins.
NOTE that we cannot distribute as (2,2,1,1) because only three bins are available, not four.
Q4: Choose the correct choice(s) regarding the following proportional logic assertion S:
S : ((P ∧ Q) → R) → ((P ∧ Q) → (Q → R))
[MSQ] (2021 SET-2)
(a) S is neither a tautology nor a contradiction
(b) S is a tautology
(c) S is a contradiction
(d) The antecedent of S is logically equivalent to the consequent of S
Ans: (b, d)
Sol: Antecedent of S : (P ∧ Q) → R
≡ ¬(P ∧ Q) ∨ R
≡ ¬P ∨ ¬Q ∨ R
Consequent of S:(P ∧ Q) → (Q → R)
≡ (P ∧ Q) → (¬Q ∨ R)
≡ ¬(P ∧ Q) ∨ (¬Q ∨ R)
≡ ¬P ∨ ¬Q ∨ (¬Q ∨ R)
≡ ¬P ∨ ¬Q ∨ R
Antecedent of S is equivalent to Consequent of S. Hence Option D is right.
A → A is a Tautology. Hence options A and C are wrong and option B is right.
Correct Answer: B ; D.
Q5: Consider the two statements.
S1: There exist random variables X and Y such that 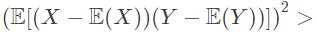 Var[X] Var[Y](
Var[X] Var[Y](
S2: For all random variables X and Y, Cov[X, Y]= 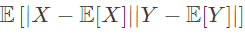
Which one of the following choices is correct? (2021 SET-1)
(a) Both S1 and S2 are true.
(b) S1 is true, but S2 is false.
(c) S1 is false, but S2 is true.
(d) Both S1 and S2 are false.
Ans: (d)
Sol: S1 : This statement is false because correlation formulae is
r = 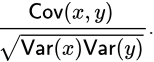
So we have r2Var(x) Var(y) = (Cov(x, y))2. By comparing above we can see that the given statement is false.
S2: This statement is false since negative covariance exists (strong negative association between random variable) but RHS of the equation always gives a positive answer.
Q6: Let p and q be two propositions. Consider the following two formulae in propositional logic.
S1 : (¬p ∧ (p ∨ q)) → q
S2 : q → (¬p ∧ (p ∨ q))
Which one of the following choices is correct? (2021 SET-1)
(a) Both S1 and S2 are tautologies.
(b) S1 is a tautology but S2 is not a tautology
(c) S1 is not a tautology but S2 is a tautology
(d) Niether S1 nor S2 is a tautology
Ans: (b)
Sol: S1 : ¬p ∧ (p ∨ q) → q
If consequence is false and hypothesis is true, then we will get False in the truth table.
Lets assume q is false. So consequence is FALSE.
Can it make Hypothesis TRUE?
Hypothesis: ¬p ∧ (p ∨ q) ≡ ¬p ∧ (p ∨ FALSE) ≡ ¬p ∧ (p) ≡ FALSE.
Hypothesis can’t be true, So we can’t get False in the Truth Table.
∴ S1 is Tautology.
S2: q → ¬p ∧ (p ∨ q)
If hypothesis is true and consequence is false, then we will get False in the truth table.
Lets assume q is True, So Hypothesis is TRUE.
Can it make Consequence FALSE ?
Consequence: ¬p ∧ (p ∨ q) ≡ ¬p ∧ (p ∨ TRUE) ≡ ¬p ∧ (TRUE) ≡ ¬p
Consequence can be false and so we can get False in the Truth Table.
∴ S2 is not Tautology.
Correct Option: B
Q7: Given that
B(a) means "a is a bear"
F(a) means "a is a fish" and
E(a,b) means "a eats b"
Then what is the best meaning of
∀x [F(x) → ∀y (E(y, x) → b(y))] (2020)
(a) Every fish is eaten by some bear
(b) Bears eat only fish
(c) Every bear eats fish
(d) Only bears eat fish
Ans: (d)
Sol: Let us translate the given statement :
For every x, if x is a fish, then for every y, if y eats x then y is bear..
This is enforcing the condition that every animal that eats a fish is a bear.. So only option d matches..
other options:
option a: Every fish is eaten by some bear
∀x(F(x) ⇒ ∃y(B(y) ∧ E(y, x)))
i.e. for all x, if x is a fish, then there is a y such that y is a bear and y eats x.
option b: Bears eat only fish
∀x(B(x) ⇒ ∀y(E(x,y)−> F (y))
i.e for every x, if x is a bear,then for all y ,if x eats y, then y is a fish.
option c: Every bear eats fish
∀x (B(x) ⇒ ∃y(F(y) ∧ E(x, y))
for all x, if x is a bear, then there is a y such that, y is a fish and x eats y.
Q8: Which one of the following predicate formulae is NOT logically valid?
Note that W is a predicate formula without any free occurrence of x. (2020)
(a) ∀x (p(x) ∨ W) ≡ ∀x p(x) ∨ W
(b) ∃x (p(x) ∧ W) ≡ ∃xp(x) ∧ W
(c) ∀x (p(x) → W) ≡ ∀xp(x) → W
(d) ∃x(p(x) → W) ≡ ∀xp(x) → W
Ans: (c)
Sol: (A)Let's consider two cases.
W-True. This makes both LHS and RHS True.
W-False. The value of LHS depends upon the truth value of ∀xP(x). Same will be the case for RHS.
Hence LHS = RHS.
(B) Using analogy in (A), we can prove that this is also valid.
W-True. LHS = RHS = True
W-False. LHS = RHS = False always.
(C)∀x (P(x) → W) ≡ ∀xP(x) → W
LHS can be re-written as ∀x(¬P(X) ∨ W) ≡ ∃xP(x) → W
(C) is not logically valid.
(D) ∃x(P(x) → W) ≡ ∃x(¬P(X) ∨ W)
Using Demorgan law for quantifiers we can again rewrite it as:
¬∀x P(x) ∨ W ≡ ∀x P(x) → W
Option (D) is valid.
Q9: Consider the first-order logic sentence
φ ≡ ∃s ∃t ∃u ∀v ∀w ∀x ∀y φ (s, t, u, v, w, x, y)
where φ(s, t, u, v, w, x, y) is a quantifier-free first-order logic formula using only predicate symbols, and possibly equality, but no function symbols. Suppose φ has a model with a universe containing 7 elements. Which one of the following statements is necessarily true? (2018)
(a) There exists at least one model of φ with universe of size less than or equal to 3.
(b) There exists no model of φ with universe of size less than or equal to 3.
(c) There exists no model of φ with universe of size greater than 7.
(d) Every model of φ has a universe of size equal to 7.
Ans: (a)
Sol: Quick logic review -
α : ∀ x ∃y y < x
Is α true for domain of all integers ?, Yes it is true. You pick any number x, I can always give you y that is less than your number x.
Is α true for domain of Non Negative integers {0, 1, 2, 3,…} ? No, it is not true. (You pick any number x) If you pick 0 then I can not give you y which is less than 0.
Definition of Model - Domain for which my sentence is true. For above sentence α, all integers is model and there can be many other models, like - real numbers.
(Definition of Co Model - Domain for which my sentence is False.)
Given that Predicate Φ ≡ ∃s ∃t ∃u ∀v ∀w ∀x ∀y Ψ(s, t, u, v, w, x, y) has a model with universe containing 7 elements. I.e. there is a domain with 7 elements which satisfies my Φ .
Now let Φ ≡ ∃s ∃t ∃u ∀v ∀w ∀x ∀y s + t + u + v + w + x + y > 200. Can you suggest me a set (domain) that is model for Φ ?. (i.e. the domain for which you can satisfy Φ ).
{10, 20, 30, 40, 50, 60, 100}, now if I choose s = 50, t = 60 and u = 100 [1] and let anyone choose values of v, w, x and y then Φ is always satisfiable for any values (or write like this - for all values) of v, w, x and y . The key point is you have to choose values of s, t and u carefully and once you fix these values then it should work for all remaining universal quantifiers values.
Actually I have problem with first element of set "10". Can I remove it and the resultant set will still work as model ? {20, 30, 40, 50, 60, 100}, Of course this is model for Φ (Why ? - take s = 50, t = 60 and u = 100 and let any other variable value be anything).
Similarly, {50, 60, 100} is also model for Φ.
Idea is once you have your s,t and u in set then that set is model (because remaining quantifiers can take any value).
Even the singleton set {100} is also model for Φ.
Now there is always one model of universe size 3, and depending on your predicate you can have model of less than size 3 too (like above singleton set).
1 s = t = u = 100 also works.
Now, Lets generalize this for better understanding-
let Φ has following model of size 7−{e1, e2, e3, e4, e5, e6, e7}, and let s = e2, t = e5, u = e1 is the only setting which works for any (for all) values of v, w, x and y, then Can we reduce model size ?- Yes, we can have a model of size 3{e1, e2, e5}. Can we reduce size further ?- We can not ( Because s = e2, t = e5, u = e1 is the only setting which works for any value of v, w, x, y). But if s = t or t = u, we can even have a model of size less than 3.
Q10: Which one of the following Boolean expressions is NOT a tautology? (2017)
(a) ((a → b) ∧ (b → c)) → (a → c)
(b) (a ↔ c) → (∼b → (a ∧ c))
(c) (a ∧ b ∧ c) → (c ∨ a)
(d) a → (b → a)
Ans: (b)
Sol: A. ((a → b) ∧ (b → c)) → (a → c)
≡ ((∼a ∨ b) ∧ (∼b ∨ c)) → (∼a ∨ c)
≡ ∼((∼a ∨ b) ∧ (∼b ∨ c)) ∨ (∼a ∨ c)
≡ ((a ∧ ∼ b) ∨ (b ∧ ∼c)) ∨ (∼a ∨ c)
≡ (∼a ∨ (a ∧ ∼ b)) ∨ ((b ∧ ∼c) ∨ c)
≡ ((∼a ∨ a) ∧ (∼a ∨ ∼b)) ∨ ((b ∨ c) ∧ (∼c ∨ c))
≡ (T ∧ (∼a ∨ ∼b)) ∨ ((b ∨ c) ∧ T)
≡ ∼a ∨ (∼b ∨ b) ∨ c
≡ ∼a ∨ T ∨ c
≡ T
B. (a ↔ c) → (∼b → (a ∧ c))
≡ ((a→c) ∧ (c → a)) → ((∼b → (a ∧ c))
≡ ∼((∼a ∨ c)∧ ( ∼ c ∨ a)) ∨ ((b ∨ (a ∧ c))
≡ ∼((a ∧ c)(∼a ∧ ∼ c)) ∨ ((b ∨ (a ∧ c))
≡ ((a ∧ ∼c) ∨ (∼a ∧ c)) ∨ ((b ∨ (a ∧c ))
≡ ((a ∧ ∼ c) ∨ c(∼a ∧ a)) ∨ b
≡ ((a ∧ ∼c) ∨ c ∨ b
≡ a ∨ b ∨ c
C. (a ∧ b ∧ c) → (c ∨ a)
≡ ∼(a ∧ b ∧ c) ∨ (c ∨ a)
≡ ∼a ∼ b ∼ c ∨ c ∨ a
≡ (a ∨ ∼a) ∨ ∼b ∨ (∼c ∨ c)
≡ T ∨ ∼ b ∨ T
≡ T
D. a → (b → a)
≡ ∼a ∨ (∼b ∨ a)
≡ (∼a ∨ a) ∨ ∼b
≡ T ∨ ∼b
≡ T
Hence, Option(B) (a ↔ c) → (∼b → (a ∧ c)) is the correct choice.
Q11: Let p, q, r denote the statements "It is raining ," It is cold", and " It is pleasant," respectively. Then the statement "It is not raining and it is pleasant, and it is not pleasant only if it is raining and it is cold" is represented by (2017 SET-2)
(a) (¬p ∧ r) ∧ (¬r → (p ∧ q))
(b) (¬p ∧ r) ∧ ((p ∧ q)→¬r)
(c) (¬p ∧ r) ∨ ((p ∧ q) → ¬r)
(d) (¬p ∧ r) ∨ (r → (p ∧ q))
Ans: (a)
Sol: 1. "It is not raining and it is pleasant" can be written as (¬p ∧ r)
2. Now, "it is not pleasant only if it is raining and it is cold" is represented by ¬r ⟹ (p ∧ q) but (p ∧ q)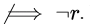 Why? Because if it is not pleasant then we can conclude it must be raining and it is cold. However, it is raining and cold does not assure that it will be unpleasant. i.e., p only if q can be written as if p then q (not double implication).
Why? Because if it is not pleasant then we can conclude it must be raining and it is cold. However, it is raining and cold does not assure that it will be unpleasant. i.e., p only if q can be written as if p then q (not double implication).
So, Anding clause 1. and 2. we get (¬p ∧ r) ∧ (¬r → (p ∧ q))
Option A is correct.
Q12: Let p, q, and r be propositions and the expression (p → q) → r be a contradiction. Then, the expression (r → p) → q is (2017 SET-1)
(a) a tautology
(b) a tautology
(c) always TRUE when p is FALSE
(d) always TRUE when q is TRUE
Ans: (d)
Sol: Given (p → q) → r is false. It is possible only when r is FALSE and (p → q) is TRUE.
Now even without checking any other option we can directly conclude option D is correct as (r → p) → q can be written as ¬(r → p) ∨ q.
Since, r is False, r → p is true and ¬(r → p) is False. So, it becomes (False ∨ q).
which is TRUE whenever q is TRUE
Hence, option (D).
Q13: Consider the first-order logic sentence F : ∀x(∃yR(x, y)). Assuming non-empty logical domains, which of the sentences below are implied by F? (2017 SET-1)
I. ∃y (∃x R(x, y))
II. ∃y (∀x R(x, y))
III. ∀y (∃x R(x, y))
IV. ¬∃x (∀y ¬R(x, y))
Ans: (b)
Sol: 1st Method: F : ∀x (∃yR(x, y))
Take option 4: ¬∃x(∀y ¬ R(x, y))
≡ ∀x (∃yR (x, y)) (Since we know that ¬∀x ≡ ∃x And ¬∃x = ∀x)
F: For all girls there exist a boyfriend. (Given)
( x for girl and y for boys)
- There exists some boys who have girlfriends. (True)
- There exists some boys for whom all the girls are girlfriend. (False)
- For all boys there exists a girlfriend. (False)
- For all girls, there exists a boyfriend (True) (Same as given statement F)
Q14: The statement (¬p) ⇒ (¬q) is logically equivalent to which of the statements below? (2017 SET-1 )
I. p ⇒ q
II. q ⇒ p
III. (¬q) ∨ p
IV. (¬p) ∨ q
(a) I only
(b) I and IV only
(c) II only
(d) II and III only
Ans: (d)
Sol: (¬P →¬Q) can also be written as (P ∨ ¬ Q), so statement 3 is correct.
Now taking the contrapositive of (¬P → ¬ Q), we get (Q → P) hence statement 2 is correct.
So, the answer is OPTION (D).
Q15: Consider the following expressions:
(i) false
(ii) Q
(iii) true
(iv) P ∨ Q
(v) ¬Q ∨ P
The number of expressions given above that are logically implied by P ∧ (P ⇒ Q) is ________. (2016 SET-2)
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (c)
Sol: 4 should be the correct answer.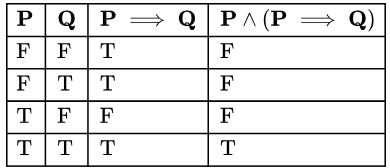 Suppose (P ∧ (P ⇒ Q)) ⟺ A (For notational convenience)
Suppose (P ∧ (P ⇒ Q)) ⟺ A (For notational convenience)
Thus for options, (i), (ii), (iii), (iv), (v)
If (A ⇒ option x) is a tautology.
then P ∧ (P ⇒ Q) logically implies option x
else P ∧ (P ⇒ Q) does not logically implies option x. Answer = 4
Answer = 4
P.S: Blank entries in the above truth table are like don't care conditions because in those rows the value of A is set to False. Hence, (A ⇒ Anything) would be set to True.
Q16: Let p,q, r, s represent the following propositions.
p: x ∈ {8, 9, 10, 11, 12}
q: x is a composite number
r: x is a perfect square
s: x is a prime number
The integer x ≥ 2 which satisfies ¬((p ⇒ q) ∧ (¬r ∨ ¬s)) is ________. (2016 SET-1)
(a) 9
(b) 10
(c) 11
(d) 12
Ans: (c)
Sol: ¬((p → q)) ∧ (¬r ∨ ¬s))
≡ (¬(¬p ∨ q)) ∨ (¬(¬r ∨ ¬s))
≡ (p ∧ ¬q) ∨ (r ∧ s)
which can be read as (x ∈ {8, 9, 10, 11, 12} AND x is not a composite number) OR (x is a perfect square AND x is a prime number)
Now for
- x is a perfect square and x is a prime number, this can never be true as every square has at least 3 factors, 1, x and x2.
So, second condition can never be true.
which implies the first condition must be true.
x ∈ {8, 9, 10, 11, 12} AND x is not a composite number
But here only 11 is not a composite number. so only 11 satisfies the above statement.
ANSWER 11.
Q17: In a room there are only two types of people, namely Type 1 and Type 2. Type 1 people always tell the truth and Type 2 people always lie. You give a fair coin to a person in that room, without knowing which type he is from and tell him to toss it and hide the result from you till you ask for it. Upon asking, the person replies the following
"The result of the toss is head if and only if I am telling the truth."
Which of the following options is correct? (2015 SET-3)
(a) The result is head
(b) The result is tail
(c) If the person is of Type 2, then the result is tail
(d) If the person is of Type 1, then the result is tail
Ans: (a)
Sol: We do not know the type of the person from whom those words are coming from and so can have two cases :
- Truth-teller : definitely implies that result of toss is Head.
- Liar : the reality will be the negation of the statement.
The negation of (x⟺y) is exactly one of x or y holds. So, we negate the statement : "The result of the toss is head if and only if I am telling the truth". This give rise to two possibilities
- it is head and lie spoken
- it is not head and truth spoken
Clearly the second one cannot be true because it cannot be a reality that the liar speaks the truth.
So, this implies that even if we negate the statement to see the reality or don't do that; The reality is that the toss yielded a Head.
Answer = option (A).
Q18: Which one of the following well formed formulae is a tautology? (2015 SET-2)
(a) ∀x ∃y R (x, y) ↔ ∃y ∀x R(x, y)
(b) (∀x [∃y R(x, y) → S(x, y)]) → ∀x ∃y S(x, y)
(c) [∀x ∃y P(x, y) → R(x, y)] ↔ [∀x ∃y(¬P(x, y)) ∨ R(x, y)]
(d) ∀x ∀y P(x, y) → ∀x ∀y P(y, x)
Ans: (c)
Sol: NOTE: “Tautology" & “Valid" are Different Concepts in First Order Logic. Tautology & Valid are Same Concepts in Propositional Logic.
Watch the following Detailed Lecture on “Tautology Vs Valid” in First Order Logic:
Note 1 :
When no information is given about Domain of variables for a First Order Logic (FOL) formula, then consider that domain for all variables in the given FOL formula is same. Unless otherwise explicitly stated, domain should be taken same for all variables of a given FOL formula.
Note 2 :
For propositional logic(PL) / Sentential logic, “Tautology” of an expression means same thing as “Validity” of that expression. But this is Not true in FOL.
Tautology/Validity in Propositional Logic :
Tautologies are a key concept in propositional logic, where a tautology is defined as a propositional formula that is true under any possible Boolean valuation of its propositional variables.
Given propositional logic expression (PLE) G is said to be Valid or Tautology iff G is ALWAYS True, regardless of which valuation is used for the propositional variables.
Some examples of Tautologies in PL :
A∨¬A
(A∨B)→(A∨B)
(A→B)→(¬B→¬A)
In propositional logic, there is no distinction between a tautology and a logically valid formula. So, In Propositional logic : Valid ≡ Tautology ≡ True
Tautology/Validity in First Order Logic(FOL) :
From Wikipedia :
The definition of tautology can be extended to sentences in predicate logic, which may contain quantifiers—a feature absent from sentences of propositional logic. Indeed, in propositional logic, there is no distinction between a tautology and a logically valid formula. In the context of predicate logic, many authors define a tautology to be a sentence that can be obtained by taking a tautology of propositional logic, and uniformly replacing each propositional variable by a first-order formula (one formula per propositional variable). The set of such formulas is a proper subset of the set of logically valid sentences of predicate logic (i.e., sentences that are true in every model).
The fundamental definition of a tautology is in the context of propositional logic. The definition can be extended, however, to sentences in first-order logic. These sentences may contain quantifiers, unlike sentences of propositional logic. In the context of first-order logic, a distinction is maintained between logical validities, sentences that are true in every model, and tautologies, which are a proper subset of the first-order logical validities. In the context of propositional logic, these two terms coincide.
A tautology in first-order logic is a sentence that can be obtained by taking a tautology of propositional logic and uniformly replacing each propositional variable by a first-order formula (one formula per propositional variable). (Note that Propositional logic manipulations can be done on the given formula, but No FOL manipulation should be done.)
For example, because A ∨ ¬A is a tautology of propositional logic, (∀x(x = x)) ∨ ¬(∀x(x = x)) is a tautology in first order logic.
Example 2:
[(∀y¬Py → ¬Px) → (Px → ¬∀y¬Py)] is a FOL Tautology. because it can be obtained from a contraposition tautology (A → ¬B) → (B → ¬A) by replacing A by ∀y¬Py and B by Px.
Example 3:
∀x ∀yP(x, y) → ∀x ∀yP(x, y) is a FOL tautology because it can be obtained from a PL Tautology A → A by replacing A with ∀x ∀y P(x, y).
Not all logical validities are tautologies in first-order logic.
For example, the sentence (∀x Rx) → ¬∃x ¬Rx
is true/valid in any first-order interpretation BUT it is Not a FOL Tautology, because it corresponds to the propositional sentence A→B which is not a tautology of propositional logic.
Example 2:
∀x (Px → Px) is NOT a FOL Tautology because it corresponds to the propositional sentence A which is not a tautology of propositional logic. Note that ∀x (Px → Px) is FOL Valid formula But Not Tautology.
Example 3:
(∀xPx) → Pc is NOT a FOL Tautology because it corresponds to the propositional sentence A → B (By replacing (∀x Px) with A and Pc with B) which is not a tautology of propositional logic. NOTE that (∀x Px) → Pc is FOL Valid formula But Not Tautology.
Example 4:
The following is an example of a logical truth that is not a tautology:
∃xCube(x) ∨ ∃x¬Cube(x). Because the validity of the argument depends on the meaning of the existential quantifier ∃ , and not just on the meaning of the connective ∨.
A sentence containing quantifiers that is a tautology is this:
∀xCube(x)∨ ¬ ∀xCube(x) which is just an instance of the tautologous form A∨ ¬ A.
So that's that.
NOTE : Every FOL Tautology is FOL validity BUT Not vice versa.
So, If a given FOL formula is Not valid, then it is Not a FOL Tautology.
Now coming back to the given question :
Option A :
Option A is NOT at all valid in FOL.
∀x ∃y R(x, y) ← ∃y ∀x R(x, y) is FOL Validity. But it is Not FOL Tautology.
∀x ∃y R(x, y) → ∃y ∀x R(x, y) is NOT FOL Validity. So, it is Not FOL Tautology as well.
Option B :
(∀x[∃yR(x, y) → S(x, y)]) → ∀x ∃y S(x, y) is NOT at all valid.
For example, Let A be a set {a,b} and let relation R on A be {(a, a)} and let relation S on A be {(a, a)} then clearly ∀x ∃y S(x, y) is false. Also (∀x [∃y R(x, y) → S(x, y)]) is true. So, we can say that option B is NOT Valid. So, it is Not a Tautology.
Option C :
[∀x∃y(P(x,y)→R(x,y))]↔[∀x∃y(¬P(x,y)∨R(x,y))] is a FOL Tautology.
Note that we can do Propositional logic manipulations, so, A → B can be written A′ ∨ B.
So, [∀x ∃y (P(x, y) → R(x, y))] ↔ [∀x ∃y(¬P(x, y) ∨ R(x, y))] is same as [∀x ∃y(¬P(x, y) ∨ R(x, y))] ↔ [∀x ∃y(¬P(x, y) ∨ R(x, y))] under only propositional logic manipulation.
Now, we can take A = [∀x ∃y(¬P(x, y) ∨ R(x, y))] and so A ↔ A is tautology in PL.
Option D :
∀x ∀yP(x, y) → ∀x ∀y P(y, x) is FOL Valid But Not FOL Tautology. NOTE that if we replace ∀x ∀y P(x, y) by A then ∀x ∀y P(y, x) is some B. But A → B is Not tautology in PL.
Q19: Consider the following two statements.
S1: If a candidate is known to be corrupt, then he will not be elected
S2: If a candidate is kind, he will be elected
Which one of the following statements follows from S1 and S2 as per sound inference rules of logic? (2015 SET-2)
(a) If a person is known to be corrupt, he is kind
(b) If a person is not known to be corrupt, he is not kind
(c) If a person is kind, he is not known to be corrupt
(d) If a person is not kind, he is not known to be corrupt
Ans: (c)
Sol: S1 = C → ¬E
S2 = K → E
so, writing them using primary operators :
S1 = ¬C ∨ ¬E
S2 = ¬K ∨ E
on using resolution principle
¬E and E cancels each other out
and conclusion = ¬C ∨ ¬K
which can also be written as K → ¬C which is translated into English as = option C
Q20: The binary operator ≠ is defined by the following truth table.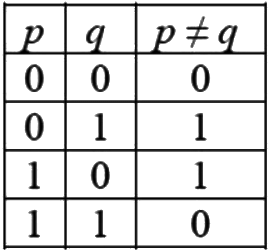
Which one of the following is true about the binary operator ≠ ? (2015 SET-1)
(a) Both commutative and associative
(b) Commutative but not associative
(c) Not commutative but associative
(d) Neither commutative nor associative
Ans: (a)
Sol: option A : as it is XOR operation.
Q21: Which one of the following is NOT equivalent to p ↔ q ? (2015 SET-1)
(a) (¬p ∨ q) ∧ (p ∨ ¬q)
(b) (¬p ∨ q) ∧ (q → p)
(c) (¬p ∧ q) ∨ (p ∧ ¬q)
(d) (¬p ∧ ¬q) ∨ (p ∧ q)
Ans: (c)
Sol: (p ⟺ q)
=(p → q) ∧ (q → p)
=(¬p ∨ q) ∧ (q → p) (Option B) As(p → q =¬p ∨ q)
=(¬p ∨ q) ∧ (¬q ∨ p) (Option A)
=(¬p ∧ ¬q) ∨ (p ∧ q) (Option D)
So, answer C is not equivanet to p ⟺ q and is the answer.
Q22: The CORECT formula for the sentence, "not all rainy days are cold" is (2014 SET-3)
(a) ∀d (Rainy(d) ∧ ∼ Cold(d))
(b) ∀d(∼ Rainy(d) → Cold(d))
(c) ∃d(∼ Rainy(d) → Cold(d))
(d) ∃d (Rainy(d) ∧ ∼ Cold(d))
Ans: (d)
Sol: Not all rainy days are cold.
In other words it says ‘‘Some rainy days are not cold"Given statement is
¬∀d[R(d) → C(d)]
≡ ¬∀d[¬R(d) ∨ C(d)]
≡ ∃d[R(d) ∧ ¬C(d)]
Hence option (D) is correct.
Q23: Consider the following statements:
P: Good mobile phones are not cheap
Q: Cheap mobile phones are not good
L: P implies Q
M: Q implies P
N: P is equivalent to Q
Which one of the following about L, M, and N is CORRECT? (2014 SET-3)
(a) Only L is TRUE.
(b) Only M is TRUE.
(c) Only N is TRUE.
(d) L, M and N are TRUE.
Ans: (d)
Sol: Correct Answer (D)
Lets break the given compound statements into atomic statements.
- A : Good mobile phones.
- B : Cheap mobile phones.
P:(A → ¬B) ⟺ (¬A ∨ ¬B)
Q:(B → ¬A) ⟺ ((¬B ∨ ¬A) ⟺ ¬A ∨ ¬B)) (Disjunction is commutative),
Hence, (P ⟺ Q) which means (P → Q) and (Q → P).
Q24: Which one of the following Boolean expressions is NOT a tautology? (2014 SET-2)
(a) ((a → b) ∧ (b → c)) → (a → c)
(b) (a → c) → (∼b → (a ∧ c))
(c) (a ∧ b ∧ c) → (c ∧ a)
(d) a → (b → a)
Ans: (b)
Sol: Another way to solve it...
Implication A → B is not tautology if B is false and A is true.
For b option Let RHS ie. b → (a ∧ c) be false ie b is false and (a ∧ c) is false.
Now, a ∧ c is false if either one of them is false.
Now, if a and c both are false then a → c is true. LHS is true and RHS is false.
So option b is not tautology.
Q25: Which one of the following propositional logic formulas is TRUE when exactly two of p, q, and r are TRUE? (2014 SET-1)
(a) ((p ↔ q) ∧ r) ∨ (p ∧ q ∧ ∼ r)
(b) (∼ (p ↔ q) ∧ r) ∨ (p ∧ q ∧ ∼ r)
(c) ((p → q) ∧ r) ∨ (p ∧ q ∧ ∼ r)
(d) (∼(p ↔ q) ∧ r) ∧ (p ∧ q ∧ ∼ r )
Ans: (b)
Sol: A. will be true if P, Q, R are true, ((p ↔ q) ∧ r) will return true. So "exactly two" is false
C. if only r is true and p and q are false, first part of implication itself will result in true
D. if r is true or false, this returns false due to r and ¬r present in conjunction. So, this is a CONTRADICTION.
B is the answer. B is true if p is TRUE and q is FALSE or vice verse, and r is true or if p and q are TRUE and r is FALSE.
PS: Actually the question should have been "TRUE ONLY when exactly two of p, q and r are TRUE".
Q26: Consider the statement
"Not all that glitters is gold"
Predicate glitters(x) is true if x glitters and predicate gold(x) is true if x is gold. Which one of the following logical formulae represents the above statement? (2014 SET-1)
(a) ∀x : glitters(x) ⇒ ¬gold(x)
(b) ∀x : gold(x) ⇒ glitters(x)
(c) ∃x : gold(x) ∧ ¬glitters(x)
(d) ∃x : glitters(x) ∧ ¬gold(x)
Ans: (d)
Sol: "Not all that glitters is gold” can be expressed as :
¬(∀x(glitters(x) ⟹ gold(x)))
(as restriction of universal quantification is same as universal quantification of a conditional statement.)
"Not all that glitters is gold" means "some glitters are not gold" which can be expressed as
∃x(glitters(x) ∧ ¬gold(x))
(as restriction of an existential quantification is same as existential quantification of a conjunction.)
So option (D) is correct.
Q27: Which one of the following is NOT logically equivalent to ¬∃x(∀y(α) ∧ ∀z(β))? (2013)
(a) ∀x(∃z(¬β) → ∀y(α))
(b) ∀x(∀z(β) → ∃z(¬α))
(c) ∀x(∀y(α) → ∃z(¬β))
(d) ∀x(∃y(¬α) → ∃z(¬β))
Ans: (a, d)
Sol: A useful rule:
∀x(α) = ¬∃(x)(¬α)
i.e.; If some property α is true for all x, then it is equivalent ot say that no x exists such that property α does not hold for it.
Starting with choices:
- ∀x(∃z(¬β) → ∀y(α))
⇒ ∀x(¬∃z(¬β) ∨ ∀y(α))
⇒ ∀x(∀z(β) ∨ ∀y(α))
⇒ ¬∃x¬(∀z(β) ∨ ∀y(α))
⇒ ¬∃x(¬∀z(β) ∧ ¬∀y(α))
So, A is not matching with the logical statement in question. - ∀x(∀z(β) → ∃y(¬α))
⇒∀ x(¬∀z(β) ∨ ∃y(¬α))
⇒¬∃x¬(¬∀z(β) ∨ ∃y(¬α))
⇒¬∃x(∀z(β) ∧ ¬∃y(¬α))
⇒¬∃x(∀z(β) ∧ ∀y(α))
Hence, matches with the given statement. - ∀x(∀y(α) → ∃z(¬β))
⇒ ∀x(¬∀y(α) ∨ ∃z(¬β))
⇒ ¬∃x¬(¬∀ y (α) ∨ ∃z(¬β))
⇒ ¬∃x(∀y(α) ∧ ¬∃z(¬β))
⇒ ¬∃x(∀y(α) ∧ ∀z(β))
Hence, matches with the given statement. - ∀x(∃y(¬α) → ∃z(¬β))
⇒ ∀x(¬∃y(¬α) ∨ ∃z(¬β))
⇒ ∀x(∀y(α) ∨ ∃z(¬β))
⇒ ¬∃x¬(∀y(α) ∨ ∃z(¬β))
⇒ ¬∃x(¬∀y(α) ∧ ¬∃z(¬β))
⇒ ¬∃x(¬∀y(α) ∧ ∀z(β))
So, D is not matching with the logical statement in question.
Thus both (A) and (D) are not logically equivalent to the given statement. In GATE 2013 marks were given to all for this question.
Q28: What is the logical translation of the following statement?
"None of my friends are perfect." (2013)
(a) ∃x(F(x) ∧ ¬P(x))
(b) ∃x(¬F(x) ∧ P(x))
(c) ∃x(¬F(x) ∧ ¬P(x))
(d) ¬∃x(F(x) ∧ P(x))
Ans: (d)
Sol:
- some of my friends are not perfect
- some of those who are not my friends are perfect
- some of those who are not my friends are not perfect
- NOT (some of my friends are perfect) / none of my friends are perfect
Correct Answer: D.
Q29: What is the correct translation of the following statement into mathematical logic?
"Some real numbers are rational" (2012)
(a) ∃x(real(x) ∨ rational(x))
(b) ∀x(real(x) → rational(x))
(c) ∃x(real(x) ∧ rational(x))
(d) ∃x(rational(x) → real(x))
Ans: (c)
Sol: Meaning of each choices:
- There exists a number which is either real or rational
- If a number is real it is rational
- There exists a number which is real and rational
- There exists a number such that if it is rational, it is real
So, (C) is the answer.
Q30: Consider the following logical inferences.
I1: If it rains then the cricket match will not be played.
The cricket match was played.
Inference: There was no rain.
I2: If it rains then the cricket match will not be played.
It did not rain.
Inference: The cricket match was played.
Which of the following is TRUE? (2012)
(a) Both I1 and I2 are correct inferences
(b) I1 is correct but I2 is not a correct inference
(c) I1 is not correct but I2 is a correct inference
(d) Both I1 and I2 are not correct inferences
Ans: (b)
Sol: I1 is a correct inference. I2 is not a correct inference as it was not mentioned what would have happened if it hadn't rained- They might have played or they might not have played.
Q31: Which one of the following options is CORRECT given three positive integers x, y and z, and a predicate
P(x) = ¬(x = 1) ∧ ∀y (∃z(x = y∗z)) ⇒ (y = x) ∨ ( y = 1) (2011)
(a) P(x) being true means that x is a prime number
(b) P(x) being true means that x is a number other than 1
(c) P(x) is always true irrespective of the value of x
(d) P(x) being true means that x has exactly two factors other than 1 and x
Ans: (a)
Sol: P(x) = (¬(x=1) ∧ ∀y(∃z(x = y∗z) ⟹ ((y = x) ∨ (y = 1)))
Statement: x is not equal to 1 and if there exists some z for all y such that product of y and z is x, then y is either the number itself or 1. This is the definition of prime numbers.
Alternative approach:
The formula
∃x ∀y ∀z[×(y, z, x) → ((y = 1) ∨ (z = 1))]
expresses the statement "there exists a prime number" (the number 1 also satisfies this statement).
Note here that × (y, z, x) is equivalent to (x = y × z).
but ¬(x = 1) removes 1 as satisfying given number in question's formula, so the option (A) is True.
Q32: Suppose the predicate F(x, y, t) is used to represent the statement that person x can fool person y at time t. which one of the statements below expresses best the meaning of the formula ∀x ∃y ∃t(¬F(x, y, t))? (2010)
(a) Everyone can fool some person at some time
(b) No one can fool everyone all the time
(c) Everyone cannot fool some person all the time
(d) No one can fool some person at some time
Ans: (b)
Sol: F(x, y, t) ⇒ person x can fool person y at time t.
For the sake of simplicity propagate negation sign outward by applying De Morgan's law.
∀x ∃y ∃t (¬F(x, y, t)) ≡ ¬∃x ∀y ∀t (F(x, y, t)) [By applying De Morgan's law.]
Now converting ¬∃x ∀y ∀t(F(x, y, t)) to English is simple.
¬∃x ∀y ∀t(F(x, y, t)) ⟹ There does not exist a person who can fool everyone all the time.
Which means No one can fool everyone all the time.
So, option (B) is correct.
|
34 videos|123 docs|72 tests
|
FAQs on Previous Year Questions: Propositional Logic - Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE)
| 1. What is propositional logic in computer science? |  |
| 2. How is propositional logic used in computer science engineering? |  |
| 3. What are the basic components of propositional logic? |  |
| 4. How is propositional logic different from predicate logic? |  |
| 5. Can propositional logic be used to solve real-world problems in computer science engineering? |  |
|
34 videos|123 docs|72 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|



















