Previous Year Questions: Set Theory | Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE) PDF Download
Q1: Let PP be the partial order defined on the set {1, 2, 3, 4} as follows
P = {(x, x)∣ x ∈ {1, 2, 3, 4}} ∪ {(1, 2), (3, 2), (3, 4)}
The number of total orders on {1, 2, 3, 4} that contain P is ______ (2024 SET-2)
(a) 2
(b) 5
(c) 7
(d) 8
Ans: (b)
Sol: The following 5 total orders will contain the given partial order (Assume left to right is bottom to top in Hasse Diagram):
Total Order 1: 1−3−2−4
Total Order 2: 1−3−4−2
Total Order 3: 3−1−2−4
Total Order 4: 3−1−4−2
Total Order 5: 3−4−1−2
Q2: Let X be a set and 2X denote the powerset of X.
Define a binary operation Δ on 2X as follows:
A Δ B = (A−B) ∪ (B−A)
Let H = (2X, Δ). Which of the following statements about H is/are correct? (2023)
(a) H is a group.
(b) Every element in H has an inverse, but H is NOT a group.
(c) For every A ∈ 2X, the inverse of A is the complement of A.
(d) For every A ∈ 2X, the inverse of A is A.
Ans: (a, d)
Sol: This is proof regarding the given question.
Here Binary operation Δ is defined on the power set of set X. i.e. 2X.
Now, say, there are two elements A and B of the set 2X and
A Δ B = (A − B) ∪ (B − A) = (A ∪ B) – (A ∩ B)
(1) Closure:
Since, 2X is a power set of set X, so it contains all the subsets of set X and so, (A ∪ B) ∈ 2X and (A ∩ B) ∈ 2X
and so, (A ∪ B) – (A ∩ B) ∈ 2X and hence, A Δ B ∈ 2X ∀A, B ∈ 2X
2) Associativity:
(i) A Δ (B Δ C) = A Δ ((B ∪ C) – (B ∩ C)) = A Δ ((B ∪ C) ∩ (B ∩ C)′)
= A Δ ((B ∪ C) ∩ (B′ ∪ C′)) = A ∪ ((B ∪ C) ∩ (B′ ∪ C′)) – A ∩ ((B ∪ C) ∩ (B′ ∪ C′))
= (A ∪ B ∪ C) ∩ (A ∪ B′ ∪ C′) ∩ (A ∩ ((B ∪ C) ∩ (B′ ∪ C′))′
= (A ∪ B ∪ C) ∩ (A ∪ B′ ∪ C′) ∩ (A′ ∪ (B′ ∩ C′) ∪ (B ∩ C))
= (A ∪ B ∪ C) ∩ (A ∪ B′ ∪ C′) ∩ (((A′ ∪ B′) ∩ (A′ ∪ C′)) ∪ (B ∩ C))
= (A ∪ B ∪ C) ∩ (A ∪ B′ ∪ C′) ∩ ((A′ ∪ B′) ∩ (A′ ∪ C′) ∪ B) ∩ ((A′ ∪ B′) ∩ (A′ ∪ C′) ∪ C)
= (A ∪ B ∪ C) ∩ (A ∪ B′ ∪ C′) ∩ (A′ ∪ C′ ∪ B) ∩ (A′ ∪ B′ ∪ C)
(ii) (A Δ B) ΔC = ((A ∪ B) – (A ∩ B)) ΔC = ((A ∪ B) ∩ (A ∩ B)′) ΔC
= (((A ∪ B) ∩ (A ∩ B)′) ∪ C) – (((A ∪ B) ∩ (A ∩ B)′) ∩ C)
= (A ∪ B ∪ C) ∩ (A′ ∪ B′ ∪ C) ∩ (C′ ∪ (A ∪ B)′ ∪ (A′ ∪ B′)′)
= (A ∪ B ∪ C) ∩ (A′ ∪ B′ ∪ C) ∩ (C′ ∪ (A′ ∩ B′) ∪ (A ∪ B))
= (A ∪ B ∪ C) ∩ (A′ ∪ B′ ∪ C) ∩ (C′ ∪ B′ ∪ A) ∩ (C′ ∪ A′ ∪ B)
Hence, Associativity satisfies. You can prove it using Venn diagram too.
(3) Identity:
Say e ∈ 2X is an identity element.
A Δ e = e Δ A = A for e ∈ 2X
A Δ e = A means (A ∪ e) – (A ∩ e) = A
It is possible when (A ∪ e) = A and (A ∩ e) = ϕ
(A ∪ e) = A is possible when e = A or e ⊂ A or e = ϕ
But e = A or e ⊂ A then (A ∩ e) ≠ ϕ and so, identity element e = ϕ
4) Inverse:
Say two elements A, B ∈ 2X and are inverse to each other.
A Δ B = B Δ A = ϕ
So, A Δ B = ϕ which means (A ∪ B) – (A ∩ B) = ϕ
It is possible when (A ∪ B) = (A ∩ B) because (A ∪ B) can’t be proper subset of A ∩ B
And (A ∪ B) = (A ∩ B) is possible when A = B
So, every element in 2X is its own inverse.
Therefore (A), (D)
One more way to prove associativity is by converting set theory operations to digital logic operations i.e. ∪ to + and ∩ to .
So, A Δ B = (A – B) ∪ (B – A) = (A ∩ B′) ∪ (B ∩ A′) = AB′ + BA′ = A ⊕ B
So, symmetric difference operation in set theory is equivalent to exor operation in digital logic.
Now, (A ⊕ B) ⊕ C = (AB′ + BA′) ⊕C = (AB′ + BA′)C′ + (AB′ + BA′)′C
= AB′C′ + BA′C′ + (A′ + B)(B′ + A)C = AB′C′ + BA′C′ + A′B′C + BAC
=A(BC + B′C′) + A′(BC′ + B′C) = A(B ⊕ C)′ + A′(B ⊕ C) = A ⊕ (B ⊕ C)
Q3: Let S be a set of consisting of 10 elements. The number of tuples of the form (A, B) such that A and B are subsets of S, and A ⊆ B is _______ (2021 SET-2)
(a) 49049
(b) 59049
(c) 3524
(d) 854
Ans: (b)
Sol: Let’s find general solution i.e. when |S| = n
Method 1 :
We want the ordered pairs (A, B) where (A ⊆ S, B ⊆ S; A ⊆ B;)
For every element x of set S, we have three choices :
- Choice 1 : x ∉ A and x ∉ B
- Choice 2 : x ∉ A and x ∈ B
- Choice 3 : x ∈ A and x ∈ B
So, for each element we have 3 choices, and we have n elements. So, answer will be 3n.
So, for the given question, answer will be 310 = 59049
NOTE : This method is nice and can be used to solve a wide variety of problems/variations very easily and in less time.
For example, Try the following variations :
Variation 1 : Find the number of ordered triples (A, B, C) where (A, B, C ⊆ S; A ⊆ B ⊆ C;)
Answer : For every element x of set S, we have 4 choices. So, 4n
Variation 2 : Find the number of ordered triples (A, B, C) where (A, B, C ⊆ S; A ⊆ B ⊇ C;)
Answer : For every element x of set S, we have 5 choices. So, 5n
Variation 3 : Find the number of ordered triples (A, B, C) where (A, B, C ⊆ S; A ⊆ B; A ⊆ C;)
Answer : For every element x of set S, we have 5 choices. So, 5n
Variation 4 : Find the number of ordered triples (A, B) where (A, B ⊆ S; A ∩ B = ϕ)
Answer : For every element x of set S, we have 3 choices. So, 3n
Many more questions can be easily solved by this method, so it is good to practice it.
Method 2 :
If we make ordered pairs (A, B) where (A ⊆ S, B ⊆ S; A ⊆ B;) such that A has k elements in it then for B we have 2(n−k) possible choices. (Because those k elemetns of A must in present in B so there is no choice for them But for each of the remaining n−k elements of S, we have 2 choices for each element)
For example, if A = {a1, a2} then how many supersets are possible for A?
There will be 2n−2 supersets of A.
So the number of ordered pairs (A, B) where (A ⊆ S, B ⊆ S; A ⊆ B;) that we have :
We can divide it into cases :
When |A| = 0 OR |A| = 1 OR |A| = 2 OR … |A| = n
When |A| = 0, there is only one such A is possible, that is A = ϕ, So, number of possible B′s = 2n; So total (A, B) pairs in this case will be 1×2n
When |A| = 1, there are nC1 such A possible, So, for each possible A, the number of possible B′s = 2n−1; So total (A, B) pairs in this case will be nC1 × 2n−1
When |A| = 2, there are nC2 such A possible, So, for each possible A, the number of possible B′s = 2n−2; So total (A, B) pairs in this case will be nC2 × 2n−2 and so on,
When |A| = n, there are nCn = 1 such A possible, So, for each possible A, the number of possible B′s = 2n−n = 20; So, total (A, B) pairs in this case will be nCn × 20
We want total possible pairs (A, B) so we can add all the above cases :
nC0 × 2n+ nC1 × 2n−1 + nC2 × 2n−2+ …nCn × 20
This is binomial expansion of (1 + 2)n = 3n
So, for the given question, answer will be 310 = 59049
Q4: If A = {x, y, z} and B = {u, v, w, x}, and the universe is {s, t, u, v, w, x, y, z}. Then 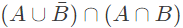 is equal to (2020)
is equal to (2020)
(a) {u, v, w, x}
(b) {x}
(c) {u, v, w, x, y, z}
(d) {u, v, w}
Ans: (b)
Sol: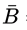 = {s, t, u, v, w, x, y, z} - {u, v, w, x} = {s, t, y, z}
= {s, t, u, v, w, x, y, z} - {u, v, w, x} = {s, t, y, z}
(A ∪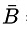 ) = {s, t, x, y, z}
) = {s, t, x, y, z}
(A ∩ B) = {x}
(A∪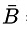 ) ∩ (A ∩ B) = {s, t, x, y, z} ∩ {x} = {x}
) ∩ (A ∩ B) = {s, t, x, y, z} ∩ {x} = {x}
But there was no such option.
Q5: Consider the first order predicate formula:
∀x[∀zz∣ x ⇒ ((z = x) ∨ (z = 1)) ⇒ ∃w(w > x) ∧ (∀z z∣w ⇒((w = z) ∨ (z = 1)))]
Here 'a|b' denotes that 'a divides b', where a and b are integers. Consider the following sets:
S1: {1, 2, 3, ..., 100}
S2: Set of all positive integers
S3: Set of all integers
Which of the above sets satisfy φ ? (2019)
(a) S1 and S2
(b) S1 and S3
(c) S2 and S3
(d) S1, S2 and S3
Ans: (c)
Sol: Only S2 satisfies given formula ψ. Hence, None of the options in correct. Wait, I know you might not agree with me, but read the whole answer first.
In all the other answers to this question, the interpretation that is given is "for every prime number(x) there exist another prime number(y) where x < y." This interpretation is WRONG. Why is this interpretation wrong ?
Divisibility Definition : If a and b are integers, a divides b if there is an integer c such that ac = b.
The notation a | b means that a divides b.
Hence, 5 is divisible by 1, 5, −1, −5. 1 is divisible by 1, −1. 1 divides everything. So does −1.
General definition of Prime : "An integer n > 1 is prime if its only positive divisors are 1 and itself.
The first few primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, . . . .
An integer n > 1 is composite if it isn’t prime."
Now, Take the following set as domain for the given formula ψ : Set of All integers.
For Set of ALL integers, the given formula ψ DOES NOT satisfy. Because for element −1 in the domain, ψ will become false. See, for x = −1, first part will become true i.e. for x = −1, (∀z z∣x ⇒ ((z = x) ∨ (z = 1))) will become true because only 1,−1 divides −1. But for x = −1, 2nd part will become false. i.e. For x = −1, There does not exist any number w > − 1 in the domain such that that w is divisible by only w, 1 because every number is also divisible by -1, −w. So, for x = −1, ψ becomes false. Hence, ψ is NOT satisfied by the set "Set of All integers."Hence, Answer should be Only S2. But none of the options match (Doesn't mean that correct answer will change because options do not match..)
Correct interpretation : Given predicate formula says "For every number x in the domain, if x is such that x is divisible by only 1,x among all the elements in the whole domain , then there exists some number w>x in the domain such that w is divisible by only 1,w among all the elements in the whole domain.Clearly, S2 satisfies ψ. Neither S1, S3 satisfies ψ.
Q6: Let U = {1, 2,,... n}. Let A = {(x, X)∣x ∈ X, X ⊆ U}. Consider the following two statements on |A|.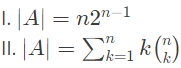
Which of the above statements is/are TRUE? (2019)
(a) Only I
(b) Only II
(c) Both I and II
(d) Neither I nor II
Ans: (c)
Sol: 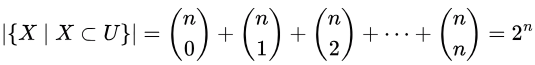
Now x can be any element of the individual subset X.
So,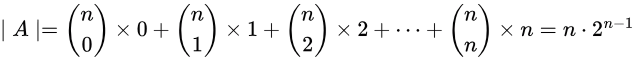
Note here that for the case when our chosen subset is empty (X = ∅), we don't have any member x ∈ X, and hence the term 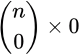 is correct.
is correct.
Proof that 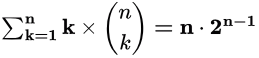
We have the Binomial Expansion: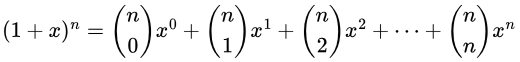 Differentiating both sides w.r.t x, we get,
Differentiating both sides w.r.t x, we get,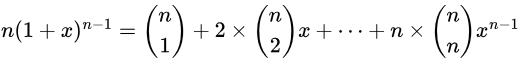
Put x = 1 to get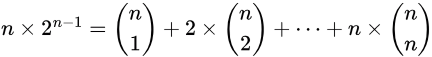
Q.E.D.
Q7: The following paradigm can be used to find the solution of the problem in minimum time:
Given a set of non-negative integer and a value K, determine if there is a subset of the given set with sum equal to K: (2018)
(a) Divide and Conquer
(b) Dynamic Programming
(c) Greedy Algorithm
(d) Branch and Bound
Ans: (b)
Sol: It's subset sum problem which required dynamic programming to solve.so option B is correct.
Q8: Let N be the set of natural numbers. Consider the following sets.
P: Set of Rational numbers (positive and negative)
Q: Set of functions from {0, 1} to N
R: Set of functions from N to {0, 1}
S: Set of finite subsets of N.
Which of the sets above are countable? (2018)
(a) Q and S only
(b) P and S only
(c) P and R only
(d) P, Q and S only
Ans: (d)
Sol: P: Set of Rational numbers are countable. Rational numbers are of the form p/q where p, q are integers. Enumeration procedure, take p + q and write down all possible values(positive and negative).
Q: Set of functions from {0, 1} to N. There are N2 such functions. Hence countable.
R: Set of functions from N to {0, 1}. There are 2N such functions.
Important theorem ⇒
If a set S is countable, then 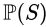 i.e 2S is uncountable.
i.e 2S is uncountable.
Hence, statement R is uncountable.
S: Set of finite subsets of N. They are countable.
Important theorem ⇒
Every subset of a countable set is either countable or finite. Hence, Option (D).
Q9: The symmetric difference of sets A = {1, 2, 3, 4, 5, 6, 7, 8} and B = {1, 3, 5, 6, 7, 8, 9} is: (2017)
(a) {1, 3, 5, 6, 7, 8}
(b) {2, 4, 9}
(c) {2, 4}
(d) {1, 2, 3, 4, 5, 6, 7, 8, 9}
Ans: (b)
Sol: A = {1, 2, 3, 4, 5, 6, 7, 8} And B = {1, 3, 5, 6, 7, 8, 9}
A (symmetric difference) B = Elements which are in A but not in B ∪ Elements which are in B but not in A
= (A - B) ∪ (B - A)
= { 2 , 4 } ∪ { 9 } = { 2 ,4 ,9 }
Option B is correct..
Q10: Consider a set U of 23 different compounds in a Chemistry lab. There is a subset S of U of 9 compounds, each of which reacts with exactly 3 compounds of U. Consider the following statements:
I. Each compound in U \ S reacts with an odd number of compounds.
II. At least one compound in U \ S reacts with an odd number of compounds.
III. Each compound in U n S reacts with an even number of compounds.
Which one of the above statements is ALWAYS TRUE? (2016 SET-2)
(a) Only I
(b) Only II
(c) Only III
(d) None
Ans: (d)
Sol: Option B should be the correct answer.
It is given that the number of compounds in U = 23 and the number of compounds in S = 9, so the number of compounds in U∖S = 23 − 9 = 14.
Considering each of these compounds as nodes of a graph G. So, vetex set of G is U and S is a subset of vertices of G.
The relation "A reacts with B" is a symmetric relation, that is A reacts with B is same as B reacts with A.
For example, consider the following reaction:
HCl + NaOH→NaCl + H2O
Here, we can say either HCl reacts with NaOH to produce NaCl + H2O or we can say that NaOH reacts with HCl to produce NaCl + H2O, so both of these statements are equivalent.
Since, the relation based on which we are going to draw the edges is symmetric, we can use an undirected edge (A, B) between any two compounds to represent the fact that A reacts with B as well as B reacts with A.
Each compound in S reacts with exactly 3 compounds in U.
It means that the degree of every node(or compound) in S is 3.
So, sum of all the degree in S = number of nodes in S × degree of each node = 9 × 3 = 27.
Now in U∖S we have 14 nodes(or compounds), thus clearly U∖S contains an even number of compounds.
Now if each compound in U∖S reacts with an even number of compounds, the sum of degrees of all the node in U∖S would be even, and consequently, the sum of degrees of all the nodes in our graph G would be odd as the sum of degrees of all the nodes in S is odd, and an odd number added with an even number produces an odd number.
But since in a graph, every edge corresponds to two degrees and the number of edges in a graph must be a (non-negative)integral value & not fractional value hence the sum of the degrees all the nodes of a graph must be even. (This is Handshaking Lemma).
So, statement III should be false(always).
Also, adding fourteen odd numbers gives an even number.
Hence, if each compound in U∖S reacts with an odd number of compounds, the sum of degrees of all the node in U∖S would be even, and consequently, the sum of degrees of all the nodes in our graph G would be odd as the sum of degrees of all the nodes in S is odd, and an odd number added with an even number produces an odd number.
Again by using Handshaking Lemma, this is not possible.
So, statement I should also be false(always).
Thus, from the previous two cases, it can be observed that to satisfy the Handshaking Lemma for G, the sum of the degrees of all the nodes U∖S must be odd. To make this happen, we must assign at least one node of U∖S, an odd degree.
If at least, one node(or compound) in U∖S would have an odd degree( or reacts with odd numbers of compounds) then we can assign degrees in such a way that the sum of the degrees of all the nodes U∖S will be odd, & thus the Handshaking Lemma would be satisfied.
Hence, statement II is the only statement which is guaranteed to be true always.
Moreover, we can also make some stronger claims from the given information like,always an odd number of compounds in U∖S reacts with an odd number of compounds andat least, one compound in S reacts with a compound in U∖S and so on.
Q11: A function 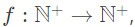 defined on the set of positive integers
defined on the set of positive integers 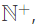 satisfies the following properties:
satisfies the following properties:
f(n) = f(n/2) if n is even
f(n) = f(n+5) if n is odd
Let R = {i∣∃j : f(j) = ii∣∃j : f(j) = i} be the set of distinct values that f takes. The maximum possible size of R is ____. (2016 SET-1)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
Sol: Let us assume: f(1) = x.
Then, f(2) = f(2/2) = f(1) = x
f(3) = f(3 + 5) = f(8) = f(8/2) = f(4/2) = f(2/1) = f(1) = x.
Similarly, f(4) = x
f(5) = f(5 + 5) = f(10/2) = f(5) = y.
So, it will have two values. All multiples of 5 will have value y and others will have value x.
Q12: Suppose U is the power set of the set S = {1, 2, 3, 4, 5, 6}. For any T ∈ U, let |T| denote the number of elements in T and T' denote the complement of T. For any T, R ∈ U, let T\R be the set of all elements in T which are not in R. Which one of the following is true? (2015 SET-3)
(a) ∀X ∈ U(∣X∣ = ∣X′∣)
(b) ∃X ∈ U ∃Y ∈U (∣X∣ = 5, ∣Y∣ = 5 and X ∩ Y = ϕ)
(c) ∀X ∈ U ∀Y ∈ U (∣X∣ = 2, ∣Y∣ = 3 and X∖Y = ϕ)
(d) ∀X ∈ U ∀Y ∈ U (X∖Y = Y′∖X′)
Ans: (d)
Sol: As X and Y elements of U, X and Y are subsets of S.
Option A is wrong consider X = {1, 2} therefore X′ = {3, 4, 5, 6}, |X| = 2 and |X′| = 4.
Option B is wrong as any two possible subsets of S with 5 elements should have atleast 4 elements in common (Pigeonhole principle). Hence, X intersection Y cannot be null.
Option C is wrong, X and Y can have any number of elements from 0 to 5. Even for the given constraint, consider X = {1, 2}, Y = {3, 4, 5} and X∖Y = {1, 2} which is not null.
Q13: Let X and Y denote the sets containing 2 and 20 distinct objects respectively and F denote the set of all possible functions defined from X to Y. Let f be randomly chosen from F. The probability of f being one-to-one is ________. (2015 SET-2)
(a) 0.2
(b) 0.5
(c) 0.75
(d) 0.95
Ans: (d)
Sol: For a function, the first element in X has 20 choices (to map to) and the second element also has 20 choices. For a one-to-one function the second element has only 19 choices left after 1 being taken by the first. So, required probability = (20 x 19)/(20 x 20) = 0.95.
Q14: The number of onto functions (surjective functions) from set x = {1, 2, 3, 4} to set Y = {a, b, c} is __________. (2015 SET-2)
(a) 12
(b) 16
(c) 9
(d) 36
Ans: (d)
Sol: We have 3 elements in set B and 4 elements in set A and surjection means every element in B must be mapped to. So, this problem reduces to distributing 4 distinct elements (r = 4) among 3 distinct bins (n = 3) such that no bin is empty, which is given by n!S(r, n), where S(r, n) is Stirling's number of 2nd kind. So, here we need S(4, 3).
We have S(r+1, n) = n∗S(r, n) + S(r, n−1)
So, Stirling numbers of second kind can be generated as follows: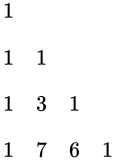 So, S(4, 3) = 6 and 3! = 6 giving, number of surjective functions = 6 ∗ 6 = 36.
So, S(4, 3) = 6 and 3! = 6 giving, number of surjective functions = 6 ∗ 6 = 36.
Q15: The cardinality of the power set of { 0, 1, 2,..., 10 } is _________. (2015 SET-2)
(a) 10
(b) 1024
(c) 2048
(d) 4096
Ans: (c)
Sol: Answer: 2048
- For any set S having n elements, the number of elements in power set P(S) is 2n.
- The term cardinality means the number of elements present in the set.
Number of elements in set = 11.
Therefore, cardinality of power set = 211 = 2048.
Q16: For a set A, the power set of A is denoted by 2A. If A = {5, {6}, {7}}, which of the following options are TRUE? (2015 SET-1)
I. ϕ ∈ 2A
II. ϕ ⊆ 2A
III. {5, {6}} ∈ 2A
IV. {5, {6}} ⊆ 2A
(a) I and III only
(b) II and III only
(c) I, II and III only
(d) I, II and IV only
Ans: (c)
Sol: Power set of A consists of all subsets of A and from the definition of a subset, ∅ is a subset of any set. So, I and II are TRUE.
5 and {6} are elements of A and hence {5,{6}} is a subset of A and hence an element of 2A. An element of a set is never a subset of the set. For that the element must be inside a set- i.e., a singleton set containing the element is a subset of the set, but the element itself is not. Here, option IV is false. To make IV true we have to do as follows:
{5, {6}} is an element of 2A. So, {{5, {6}}} ⊆ 2A.
So, option C.
Q17: Let x and Y be finite sets and f : x→Y be a function. Which one of the following statements is TRUE? (2014 SET-3)
(a) For any subsets A and B of x, |f(A ∪ B)| = |f(A)| + |f(B)|
(b) For any subsets A and B of x, f(A ∩ B) = f(A) ∩ f(B)
(c) For any subsets A and B of x, |f(A ∩ B)| = min{|f (A)| ,|f(B)|}
(d) For any subsets S and T of Y, f−1(S ∩ T) = f−1(S) ∩ f−1(T)
Ans: (d)
Sol: 3 out of 4 options can be eliminated with the help of a counter example.
Let X = {a, b, c} and Y = {1, 2}
A Function f maps each element of X to exactly one element in Y.
Let f(a) = 1, f(b) = 1, f(c) = 1 and A = {a}, B = {b, c}
(A)
- LHS : |f(A ∪ B)| = |f({a, b, c})| = |{1}| = 1
- RHS : |f(A)| + |f(B)| = 1 + 1 = 2 ,
- LHS ≠ RHS
B)
- LHS : f(A ∩ B) = f({}) = {}.
- RHS : f(A) ∩ f(B) = {1} ∩ {1} = {1}
- LHS ≠ RHS
C)
- LHS : |f(A ∩ B)| = |f({})| = |{}| = 0
- RHS : min{|f(A)|, |f(B)|} = min(1, 1) = 1
- LHS ≠ RHS
(D) Its easy to see that this is true because in a function a value can be mapped only to one value. The option assumes inverse of function f exists.
Answer is D.
Q18: Consider the following relation on subsets of the set S of integers between 1 and 2014. For two distinct subsets U and V of S we say U < V if the minimum element in the symmetric difference of the two sets is in U.
Consider the following two statements:
S1: There is a subset of S that is larger than every other subset.
S2: There is a subset of S that is smaller than every other subset.
Which one of the following is CORRECT? (2014 SET-2)
(a) Both S1 and S2 are true
(b) S1 is true and S2 is false
(c) S2 is true and S1 is false
(d) Neither S1 nor S2 is true
Ans: (a)
Sol: Symmetric difference (SD) - suppose A and B are 2 sets then symmetric difference of A and B is (A − B) ∪ (B − A) = (A ∪ B)−(A ∩ B).
In question : U < V if the minimum element in the symmetric difference of the two sets is in U . Example: {1,2,3}<{2,3,4,5,6}
Symmetric difference is {1} ∪ {4, 5, 6}.
Now Consider a smaller set. Suppose S = {1, 2, 3, 4}
Now the given 2 statements are about smallest and largest subset. So, considering set S and ∅ (empty set) will be helpful.
First take U = {1, 2, 3, 4} and V = {1, 2} (we can take any set other than ∅ and S)
SD = {3, 4} (just exclude the elements which are common in the 2 sets)
Minimum element of SD is 3 which is in U and if we observe carefully minimum element will always be in U. Whatever the V is.
So, according to the question {1, 2, 3, 4} is smaller than any other subset of S. S2 is true.
Now consider
U = ∅ and V = {1, 2} (we can take any subset of S)
SD = {1, 2}
The symmetric difference will always be equal to V. So minimum element of SD will always exist in V when U is ∅.
So, according to the que, ∅ is greater than any other subset of S. S1 is also true.
This is true even when S = {1, 2, 3 ,…, 2014}.
So, answer is A. Both S1 and S2 are true.
Q19: The number of elements in the power set of the set {{A, B}, C} is (2013)
(a) 7
(b) 8
(c) 3
(d) 4
Ans: (d)
Sol: No of elements of power set will be 2n . here n is element of set so given set has 2 elements then power set has 22 = 4 elements (Ans option d)
which are {ϕ, {A, B}, {C}, { { A, B}, C} }
Q20: A binary operation ⊕ on a set of integers is defined as x ⊕ y = x2+y2. Which one of the following statements is TRUE about ⊕? (2013)
(a) Commutative but not associative
(b) Both commutative and associative
(c) Associative but not commutative
(d) Neither commutative nor associative
Ans: (a)
Sol: Answer is (A) Commutative but not associative.
y ⊕ x = y2+x2 = x⊕y. Hence, commutative.
(x ⊕ y) ⊕ z = (x2+ y2) ⊕ z = (x2+y2)2 + z2
x ⊕ (y ⊕ z) = x ⊕ (y2 + z2) = x2 + (y2 + z2)2
So, ((x ⊕ y) ⊕ z) ≠ (x ⊕ (y ⊕ z)), hence not associative.
Q21: Which one of the following is true? (2011)
(a) R ∩ S = (R ∪ S)−[(R − S) ∪ (S − R)]
(b) R ∪ S = (R ∩ S) − [(R − S) ∪ (S − R)]
(c) R ∩ S = (R ∪ S) − [(R − S) ∩ (S − R)]
(d) R ∩ S = (R ∪ S) ∪ (R − S)
Ans: (a)
Sol:
A. R ∩ S = (R∪S) − [(R−S) ∪ (S−R)]
{ 2 } = { 1 , 2 , 3 } - [ {1} ∪ {3} ]
{ 2 } = { 2 }
B. R ∪ S = (R ∩ S) − [(R − S) ∪ (S − R)]
{1 , 2 , 3} ≠ { 2 } - [1, 3]
C. R ∩ S = (R ∪ S) − [(R−S) ∩ (S−R)]
{ 2 } ≠ { 1 , 2 , 3 } - [ 1 ∩ 3 ]
D. R ∩ S = (R ∪ S) ∪ (R−S)
{ 2 } = { 1 , 2 , 3 } ∪{1}
{ 2 } ≠ { 1 , 2 , 3 }
Hence.Option(A) R∩S = (R ∪ S) − [(R − S) ∪ (S − R)] is the correct choice.
Q22: What is the possible number of reflexive relations on a set of 5 elements? (2010)
(a) 210
(b) 215
(c) 220
(d) 225
Ans: (c)
Sol: A relation consists of set of ordered pairs (a, b). Here, a can be chosen in n ways and similarly, b can be chosen in n ways. So, totally n2 possible ordered pairs are possible for a relation. Now each of these ordered pair can either be present in the relation or not- 2 possibilities for each of the n2 pair. So, total number of possible relations = 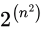
Now, for a relation R to be reflexive, ordered pairs {(a, a)∣a ∈ S}, must be present in R. i.e.; the relation set R must have n ordered pairs fixed. So, number of ordered pairs possible is n2−n and hence total number of reflexive relations is equal to 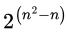 for n = 5, answer will be,
for n = 5, answer will be, 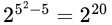 .
.
Therefore, option C is correct.
|
34 videos|123 docs|72 tests
|
FAQs on Previous Year Questions: Set Theory - Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE)
| 1. What is a set in set theory? |  |
| 2. What is the cardinality of a set? |  |
| 3. What is the intersection of two sets? |  |
| 4. How is the union of two sets defined in set theory? |  |
| 5. What is the difference between a set and a subset? |  |
|
34 videos|123 docs|72 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|














