Previous Year Questions: Shortest Path | Algorithms - Computer Science Engineering (CSE) PDF Download
Q1: Let G = (V, E) be an undirected unweighted connected graph. The diameter of G is defined as:
Let M be the adjacency matrix of G.
Define graph G2 on the same set of vertices with adjacency matrix N, where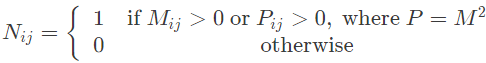
Which one of the following statements is true? (2021 SET-1)
(a) diam(G2) ≤ [diam(G)/2]
(b) [diam(G)/2] < diam (G2) < diam(G)
(c) diam(G2) = diam(G)
(d) diam(G) < diam (G2) ≤ 2 diam(G)
Ans: (a)
Sol: A walk consists of an alternating sequence of vertices and edges consecutive elements of which are incident that begins and ends with a vertex.
In simple words, Walk from vertex w to v is sequence of "adjacent edges", starting from w, ending at v, possibly with repetition of vertices or edges or both. Length of a walk is the number of edges on it.
The Adjacency Matrix of a Graph :
The adjacency matrix M of a undirected graph is defined by numbering the vertices, say from 1 up to n, an then putting Mij = Mji = 1 if there is an edge from i to j, and Mij = 0 otherwise.
We can do the same for a digraph: putting Mij = 1 if there is an edge from i to j, and Mij = 0 otherwise.
Powers of the Adjacency Matrix :
Let G be a graph, n ∈ N, Let M be the adjacency matrix of G.
The powers of the adjacency matrix counts things. In particular,
Entry i, j in Mn gives the number of walks from i to j of length n.
The proof is by induction argument. For example, the number of walks of length 2 is the number of vertices k such that there is an edge from i to k and an edge from k to j. And this is exactly the i, j entry in M2, by the definition of matrix multiplication.
Also, NOTE that for any graph G (directed or undirected), we can see that, every entry in adjacency matrix
basically tells us that Number of walks of length 1 between the corresponding vertices of that entry, So, if Mij is 1, it means there is walk of length 1 from i to j, which is basically edge from i to j.
Coming to the given question, for undirected connected graph G, M is its adjacency matrix. So, every non-zero entry Mij in M tells us that there is a walk of length 1 between vertices i and j in G.
Given P = M2, So, every non-zero entry Pij in P tells us that there is a walk of length 2 between vertices i and j in G.
(In particular, every entry Pij in P tells us the number of walks of length 2 between vertices i and j in G.)
By the definition of matrix N, Nij is 1 if either Mij is 1 or Pij is 1, So, we can say that Nij is 1 if there is a walk of length 1 or 2 or both between vertices i, j in G.
N is adjacency matrix of graph G2, So, in Graph G2, we have edge between i, j if there is walk of length 1 or 2 between i, j in G.
So, conclusive point is that :
To get G2 from G, we need to keep the G as it is, but also we need to add edge between vertex w, u if there is walk of length 2 between w, u. For undirected connected graph of at least two vertices, it will also bring self loops for every vertex.
So, diameter of G2 will definitely become almost half of diameter of G.
If Diameter of G is odd number, say d = 7, then Diameter of G2 will become [d/2] = 4.
If Diameter of G is even number, say d = 6, then Diameter of G2 will become [d/2] = 3.
Option A is correct. But I think (Point me out if I am wrong) that Diam (G2) = [Diam(G)/2].
Q2: Let G = (V, E) be a directed, weighed graph with weight function w : E → R. For some function f : V → R, for each edge (u, v) ∈ E, define w' (u, v) as w(u, v) + f (u) - f(v).
Which one of the options completes the following sentence so that it is TRUE?
"The shortest paths in G under w are shortest paths under w' too,__________". (2020)
(a) for every f : V→R
(b) if and only if ∀u ∈ V, f(u) is positive
(c) if and only if ∀u ∈ V, f(u) is negative
(d) if and only if f(u) is the distance from s to u in the graph obtained by adding a new vertex s to G and edges of zero weight from s to every verex of G
Ans: (a)
Sol: For any mapping of vertices to real values, the shortest paths won't change. All intermediate nodes values get canceled on any path you take and what you're left with is only the source and destination node values which would add up to cost on any path. Hence, the shortest paths would still be the same.
PS: Option D is wrong because of the "if and only if" clause in it. If it were "if", it would be correct. The condition given is sufficient but not necessary. Hence, "only if" is incorrect in the option. Basically it is saying f(u) would be 0 for all vertices since they're connected to a new vertex s with zero weighted edge. Similarly options B and C are also wrong for the same reason.
Q3: Let G = (V, E) be any connected undirected edge-weighted graph. The weights of the edges in E are positive and distinct. Consider the following statements:
(1) Minimum spanning tree of G is always unique.
(II) Shortest path between any two vertices of G is always unique.
Which of the above statements is/are necessarily true? (2017 SET-1)
(a) (1) only
(b) (II) only
(c) Both (I) and (II)
(d) Neither (1) nor (II)
Ans: (a)
Sol:
- MST is not unique only when edges are not distinct. Here the edges are distinct. Be careful for the keyword DISTINCT.
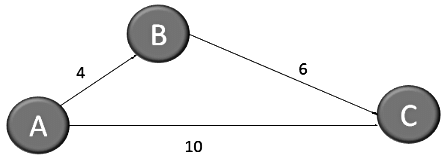
- Shortest Path can be different even if the edges are distinct. Example is shown below. Shortest path from A to C is not unique here.
Q4: Consider the weighted undirected graph with 4 vertices, where the weigh to edge {i, j} is given by the entry Wij in the matrix W.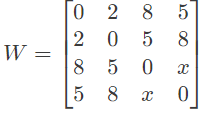
The largest possible integer value of x, for which at least one shortest path between some pair of vertices will contain the edge with weight x is______. (2016 SET-1)
(a) 8
(b) 10
(c) 12
(d) 13
Ans: (c)
Sol: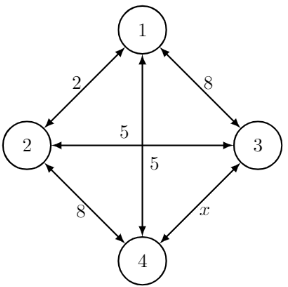
Let us list down the shortest edge between each pair of vertices x, y in the graph
- Case 1: Let us say x < 3. Say x = 2.
When we put x = 2 the above table is modified as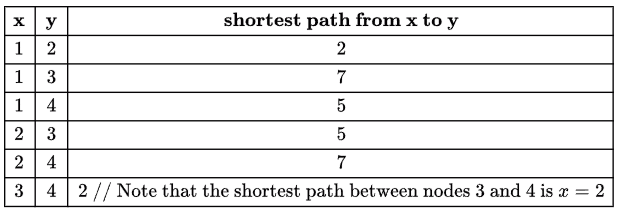
- Case 2: 3 ≤ x < 13. Let's say x = 12. The table is now modified as

Now the question asks you to find the largest possible integer value of x such that shortest path between at least one pair of nodes in the graph is equal to x. For values x = 2, 3, 4,..., 12 the shortest path between node 3 and 4 is equal to x.
The largest among this is x = 12. So the answer is 12
PS: If the question is modified as "The largest possible integer value of x, for which the shortest path between some pair of vertices is guaranteed to contain the edge with weight x is"
then the answer will be 11.
Correct Answer: 12.
Q5: Let G be a weighted connected undirected graph with distinct positive edge weights. If every edge weight is increased by the same value, then which of the following statements is/are TRUE? (2016 SET-1)
P: Minimum spanning tree of G does not change
Q: Shortest path between any pair of vertices does not change
(a) P only
(b) Q only
(c) Neither P nor Q
(d) Both P and Q
Ans: (a)
Sol: Statement P is true.
For statement Q consider a simple graph with 3 nodes.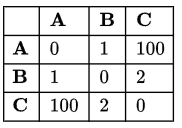
Shortest path from A to C is A - B - C = 1 + 2 = 3
Now if the value of each edge is increased by 100,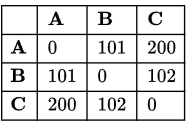
The shortest path from A to C is A - C = 200, (A - B - C = 101 + 102 = 203)
Hence, option A is correct.
Q6: Let G = (V, E) be a simple undirected graph, and s be a particular vertex in it called the source. For a ∈ V, let d(x) denote the shortest distance in G from s to x. A breadth first search (BFS) is performed starting at s. Let T be the resultant BFS tree. If (u, v) is an edge of G that is not in T, then which one of the following cannot be the value of d(u)-d(v)? (2015 SET-1)
(a) -1
(b) 0
(c) 1
(d) 2
Ans: (d)
Sol: d(u) - d(v) = 0 is possible when both u and v have an edge from from a common node t and t is in the shortest path from s to u and v.
d(u) - d(v) = 1 is possible when v and another node t are in the shortest path from s to u ad both t and v are siblings- same distance from s to both t and v causing t - u edge to be in BFS tree and not v - u
d(u) - d(v) = -1 is possible as explained above by interchanging u and v.
d(u) - d(v) = 2 is not possible. This is because on BFS traversal we either visit u first or v. Let's take u first. Now, we put all neighbors of u on queue. Since v is a neighbour and v is not visited before as assumed, d(v) will become d(u) + 1 Similarly, for v being visited first.
Q7: Consider the tree arcs of a BFS traversal from a source node W in an unweighted, connected, undirected graph. The tree T formed by the tree arcs is a data structure for computing (2014 SET-2)
(a) the shortest path between every pair of vertices
(b) the shortest path from W to every vertex in the graph.
(c) the shortest paths from W to only those nodes that are leaves of T.
(d) the longest path in the graph.
Ans: (b)
Sol: BFS always has a starting node. It does not calculate shortest path between every pair but it computes shortest path between W and any other vertex.
Correct Answer: B
Q8: What is the time complexity of Bellman-Ford single-source shortest path algorithm on a complete graph of n vertices? (2013)
(a) Θ(n2)
(b) Θ(n2logn)
(c) Θ(n3)
(d) Θ(n3logn)
Ans: (c)
Sol: Time complexity of Bellman-Ford algorithm is Θ(|V||E|) where |V| is number of vertices and |E| is number of edges. If the graph is complete, the value of | E| becomes Θ(|V|2). So overall time complexity becomes Θ(|V|3). And given here is n vertices. So, the answer ends up to be Θ(n3).
Correct Answer: C
Q9: Consider the directed graph shown in the figure below. There are multiple shortest paths between vertices S and T. Which one will be reported by Dijkstra's shortest path algorithm? Assume that, in any iteration, the shortest path to a vertex v is updated only when a strictly shorter path to v is discovered (2012)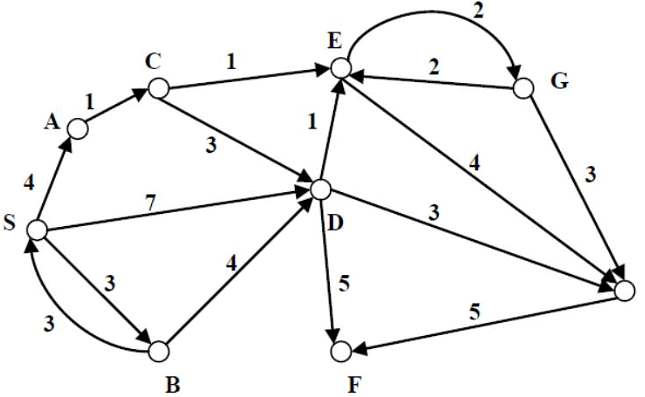
(a) SDT
(b) SBDT
(c) SACDT
(d) SACET
Ans: (d)
Sol: Relaxation at every vertex is as follows:
Note that the next picked vertex corresponds to the next row in Table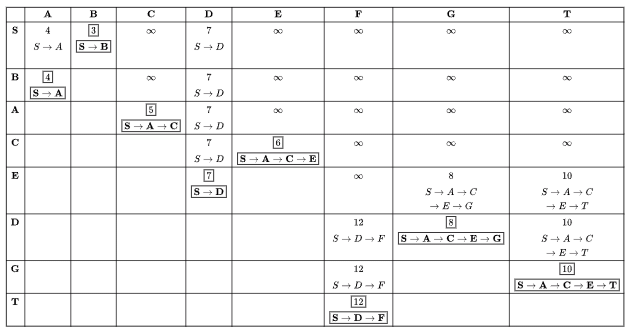
For S to T shortest path is
Q10: Consider a complete undirected graph with vertex set {0, 1, 2, 3, 4}. Entry Wij in the matrix W below is the weight of the edge {i, j}.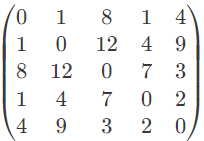
What is the minimum possible weight of a path P from vertex 1 to vertex 2 in this graph such that P contains at most 3 edges? (2010)
(a) 7
(b) 8
(c) 9
(d) 10
Ans: (b)
Sol: 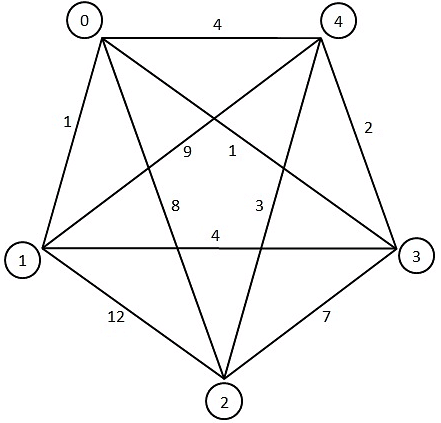
Answer is (B) 8. The possible path is: 1 - 0, 0 - 4, 4 - 2.
Q11. Which of the following statement(s) is/are correct regarding Bellman-Ford shortest path algorithm?
P. Always finds a negative weighted cycle, if one exists.
Q. Finds whether any negative weighted cycle is reachable from the source. (2009)
(a) P only
(b) Q only
(c) both P and
(d) Neither P nor Q
Ans: (b)
Sol: Bellman-ford Algorithm
Single source shortest Path O(VE)
Relax every edge once in each iteration
at max (V - 1) edges can be there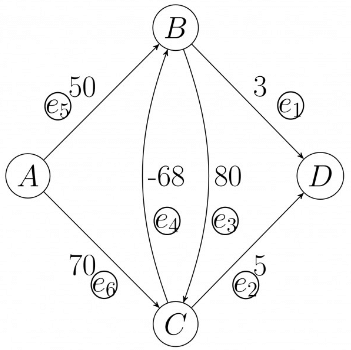
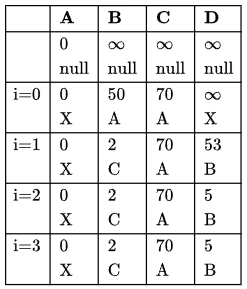
As we can see that the last step is the verification step. In that step, values remained unchanged. If there was a negative edge weight cycle reachable from source, then at verification step also, those values will be different from the values above.
In case the cycle is not reachable from source then we can see that they will be at ∞ distance(or cost) from the source from the beginning till the last step. As take anything away from the ∞ it will still be infinite.
But it can also be the case that there are some points which are not forming a cycle and are still unreachable from source, those also will be at co distance from the source from the beginning till end.
Hence, we won't be able to make a distinction among the cycle and such vertices. Thus, we say that this algorithm can detect negative edge weight cycles only if they are reachable from the source.
Answer is option B.
Q12: 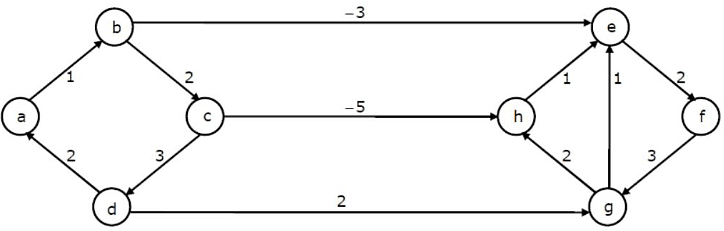
Dijkstra's single source shortest path algorithm when run from vertex a in the above graph, computes the correct shortest path distance to (2008)
(a) only vertex a
(b) only vertices a, e, f, g, h
(c) only vertices a, b,
(d) all the vertices
Ans: (d)
Sol: D. all the vertices. Just simulate the Dijkstra's algorithm on it. Dijkstra's algorithm is not meant for graphs with negative-edge-weight-cycle, but here it does give the correct shortest path.
Q13: Djikstra's algorithm is used to (2007)
(a) Create LSAs
(b) Flood an internet with information
(c) Calculate the routing tables
(d) Create a link state database
Ans: (c)
Sol: Calculation of routing tables, as djikstra algorithm calculates shortest path for all
the nodes in link state routing protocol.
Q14: Consider a weighted, undirected graph with positive edge weights and let uv be an edge in the graph. It is known that the shortest path from the source vertex s to u has weight 53 and the shortest path from s to v has weight 65. Which one of the following statements is always TRUE? (2007)
(a) Weight (u, v) ≤ 12
(b) Weight (u, v) = 12
(c) Weight (u, v) ≥ 12
(d) Weight (u, v) > 12
Ans: (c)
Sol: C. Weight (u, v) ≥ 12
If weight (u, v) < 12, then the min. weight of (s, v) = weight of (s, u) + weight of (u, v) = 53 + (<12) will be less than 65.
Q15: In an unweighted, undirected connected graph, the shortest path from a node S to every other node is computed most efficiently, in terms of time complexity, by (2007)
(a) Dijkstra's algorithm starting from S.
(b) Warshall's algorithm
(c) Performing a DFS starting from S.
(d) Performing a BFS starting from S.
Ans: (d)
Sol: Dijkstra's and Warshall's algorithms are used only for weighted graphs.
Both DFS and BFS can be used for finding path between 2 vertices in undirected and unweighted graph but BFS can only give the shortest path as concerned in given question.
So, BFS is answer.
Note: Finding only path (DFS) and finding shortest path (BFS) matters a lot.
Q16: To implement Dijkstra's shortest path algorithm on unweighted graphs so that it runs in linear time, then data structure to be used is (2006)
(a) Queue
(b) Stack
(c) Heap
(d) B-Tree
Ans: (a)
Sol: We can find single source shortest path in unweighted graph by using Breadth First Search (BFS) algorithm by using "Queue" data structure, in time O(m + n) (i.e. linear with respect to the number of vertices and edges.)
Q17: Let G be a directed graph whose vertex set is the set of numbers from 1 to 100. There is an edge from a vertex i to a vertex j if either j = i + 1 or j = 3i. The minimum number of edges in a path in G from vertex 1 to vertex 100 is (2005)
(a) 4
(b) 7
(c) 23
(d) 99
Ans: (b)
Sol: Edge set consists of edges from i to j using either
1. j = i + 1 (or)
2. j = 3i.
Second option will help us reach from 1 to 100 rapidly. The trick to solve this question is to think in reverse way. Instead of finding a path from 1 to 100, try to find a path from 100 to 1.
The edge sequence with minimum number of edges is
1 → 3 → 9 → 10 → 11 → 33 → 99 - 100 which consists of 7 edges.
The answer is option (B).
Q18: Let s and t be two vertices in a undirected graph G=(V, E) having distinct positive edge weights.
Let [X, Y] be a partition of V such that S∈X and t∈Y. Consider the edge e having the minimum weight amongst all those edges that have
one vertex in X and one vertex in Y.
Let the weight of an edge e denote the congestion on that edge. The congestion on a path is defined to be the maximum of the congestions on the edges of the path. We wish to find the path from s to t having minimum congestion. Which one of the following paths is always such a path of minimum congestion? (2005)
(a) a path from s to t in the minimum weighted spanning tree
(b) a weighted shortest path from s to t
(c) an Euler walk from s to t
(d) a Hamiltonian path from s to t
Ans: (a)
Sol: Here answer should be A.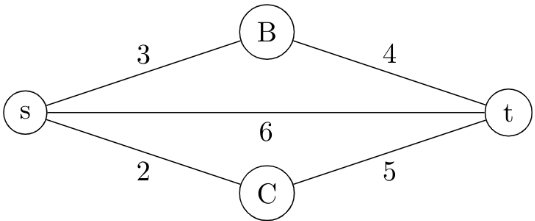
Here, shortest path will give 6.
Spanning tree contains edges of weights 2, 3, 4 so congestion in this case is max (2, 3, 4), that is, 4. For path s to t, overall congestion is max(3, 4) = 4 but total weight is 7.
Option C and D are I think not related to this question.
Q19: Let G(V,E) be an undirected graph with positive edge weights. Dijkstra's single source shortest path algorithm can be implemented using the binary heap data structure with time complexity: (2005)
(a) O(|V|2)
(b) O(|E|+ |V| log |V|)
(c) O(|V| log |V|)
(d) O((|E| + |V|) log |V|)
Ans: (d)
Sol: Option (D): Binary heap. |E| decrease key operations and each taking O (log |V|) time + |V| extract-min operations each taking O (log |V|).
Option (B): Fibonacci heap. |E| decrease key operations and each taking O(1) time +|V| extract-min operations each taking O (log |V|).
Option (A): Array. Finding min-vertex in each iteration takes O(V) and this needs to be done |V| times.
Binomial Heap is same as Binary heap here, as the critical operations are decrease key and extract-min.
Q20: Suppose we run Dijkstra's single source shortest-path algorithm on the following edge-weighted directed graph with vertex P as the source.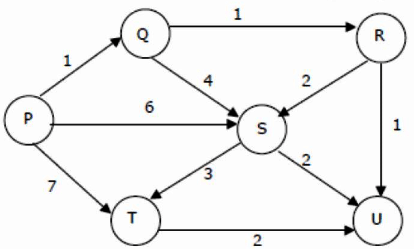
In what order do the nodes get included into the set of vertices for which the shortest path distances are finalized? (2004)
(a) P,Q,R,S,T,U
(b) P,Q,R,U,S,T
(c) P,Q,R,U,T,S
(d) P,Q,T,R,U,S
Ans: (b)
Sol: In Dijkstra's algorithm at each point we choose the vertex with the shortest distance from the set of vertices in the shortest path found so far and add the edge connecting it to the shortest path.
Q21: Let G = (V,E) be an undirected graph with a sub-graph G1 = (V1,E1), Weight are assigned to edges of G as follows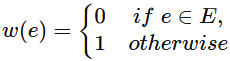
A single-source shortest path algorithm is executed on the weighted graph (V, E, w) with an arbitrary vertex v1 of V1 as the source. Which of the following can always be inferred from the path costs computed? (2003)
(a) The number of edges in the shortest paths from v1 to all vertices of G
(b) G1 is connected
(c) V1 forms a clique in G
(d) G1 is a tree
Ans: (b)
Sol: After applying the shortest path algorithm, check cost of vertex from source to every vertex in G1. If G1 is connected all these costs must be 0 as edge weights of subgraph G1 is 0 and that should be the shortest path. If cost is not 0, to at least one vertex in G1 (not necessarily G), then G1 is disconnected.
Q22: Consider the undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r,u) and d(r,v) be the lengths of the shortest paths form r to u and v respectively in G. If u is visited before v during the breadth-first traversal, which of the following statements is correct? (2001)
(a) d(r, u) < d(r, v)
(b) d(r, u) ≤ d(r, v)
(c) d(r, u) > d(r, v)
(d) None of the above
Ans: (b)
Sol: BFS is used to count shortest path from source (If all path costs are 1)
Now, if u is visited before v it means 2 things:
- Either u is closer to r, or,
- If u & v are same distance from r, then our BFS algo chose to visit u before v.
|
81 videos|113 docs|34 tests
|
FAQs on Previous Year Questions: Shortest Path - Algorithms - Computer Science Engineering (CSE)
| 1. What is the Dijkstra's algorithm used for in the context of shortest path problems? |  |
| 2. How does Dijkstra's algorithm differ from other shortest path algorithms like Bellman-Ford? |  |
| 3. Can Dijkstra's algorithm handle graphs with cycles? |  |
| 4. Is Dijkstra's algorithm guaranteed to find the shortest path in all cases? |  |
| 5. How can Dijkstra's algorithm be optimized for better performance in large graphs? |  |
















