Previous Year Questions: Sorting | Algorithms - Computer Science Engineering (CSE) PDF Download
Q1: Consider the following array.
Which algorithm out of the following options uses the least number of comparisons (among the array elements) to sort the above array in ascending order? (2021 SET-1)
(a) Selection sort
(b) Merge sort
(c) Insertion sort
(d) Quicksort using the last element as pivot
Ans: (c)
Sol:
The given array is already sorted in ascending order.
For already sorted array, different sorting algorithms behave as following :
Selection sort :
No matter how the data is arranged, there would always be comparisons and swaps made and so the time complexity for best,average and worst case is : O(n2).
In first pass, we need n -1 comparisons (Or n comparisons, depending on the implementation)
In second pass, we need n - 2 comparisons (Or n - 1 comparisons, depending on the implementation) and so on.
So, the number of comparisons required by a selection sort of n items can be computed by the formula:
(n - 1) + (n - 2) + ... + 1 = (n)(n - 1)/2
Or
Number of selection sort comparisons = (n + 1)(n)/2
Basically, number of comparisons is Θ(n2) in all cases.
Insertion Sort :
When elements are already sorted in desired order, there are no swaps and the correct position of the
element in the sorted list is the current index itself. The time complexity is: O(n)
Number of comparisons = n - 1
Comparisons in total: 1 + 1 +... + 1 = n − 1 ∈ Θ(n).
Merge Sort :
We are dividing the list into two halves, no matter if the list is sorted or not. But if the array is sorted, while merging the list,
there are no swaps merging results into an array itself. Thus, the best, average and worst case time complexity is: O(n log n)
Number of comparisons, in all cases, will be O(n log n)
Quick Sort:
If we use the last or first element as pivot, then Quick Sort will give worst case performance if the elements
are in a sorted or reverse sorted manner. So, for the given array in the question, Quick Sort will behave in worst manner and will take O(n2) comparisons.
The best and average case time complexity is: O(n log n)
Number of comparisons, in best case, will be O(n log n)
So, answer will be insertion sort.
Q2: Of the following sort algorithms, which has execution time that is least dependant on initial ordering of the input? (2020)
(a) Insertion sort
(b) Quick sort
(c) Merge sort
(d) Selection sort
Ans: (c)
Sol:
In insertion sort, if the array is already sorted then it takes O(n). If the array is reverse sorted then it takes O(n2).
In quick sort, if the array is already sorted or sorted in the reverse order, then it takes O(n2).
The best and worst-case performance of the Selection sort is O(n2) only. But in case the array is already sorted then fewer swaps take place.
In the case of Merge Sort, the time complexity is always O(nlogn) for all the cases. In short, Merge sort is Non-Adaptive in nature but rest of algorithms are.
Adaptive Sorting:
If order of the elements to be sorted of an input array matters (or) affects the time complexity of a sorting algorithm, then that algorithm is called "Adaptive" sorting
Q3: An array of 25 distinct elements is to be sorted using quicksort. Assume that the pivot element is chosen uniformly at random. The probability that the pivot element gets placed in the worst possible location in the first round of partitioning (rounded off to 2 decimal places) is (2019)
(a) 0.08
(b) 0.0016
(c) 0.04
(d) 0.0008
Ans: (a)
Sol: Worst case of quicksort, if pivot element is Minimum or Maximum.
Total elements = 25
For worst case number of candidates = 2
P =2/25 = 0.08
Q4: Of the following sorting algorithms, which has a running time that is least dependent on the initial ordering of the input? (2018)
(a) Merge Sort
(b) Insertion Sort
(c) Selection Sort
(d) Quick Sort
Ans: (a)
Sol: Answer will be Merge Sort
In merge sort we divide the array in 2 subarrays, then again divide it in 2 subarrays, like that it divide entire array
And time of merging, we merge 2 subarrays, again merge next two sub arrays
So, here input hardly matters to sort the array But if we consider quick sort, here initial ordering matters.
Because if the array is increasing or decreasing order, quick sort takes maximum running time to find,
is the array is sorted or not Similarly, for insertion sort and selection sort, for sorted and unsorted input running time differs in every case
Q5: Given two sorted list of size m and n respectively. The number of comparisons needed the worst case by the merge sort algorithm will be: (2018)
(a) m-n
(b) maximum of m and n
(c) minimum of m and n
(d) m+n-1
Ans: (d)
Sol: option d
worst case comparisons in merge sort is o(m+n-1)
Q6: The number of swappings needed to sort the numbers 8, 22, 7, 9, 31, 5, 13 in ascending order using bubble sort is (2017)
(a) 11
(b) 12
(c) 13
(d) 10
Ans: (d)
Sol: Answer is 10. All swaps are in following order:
8,7,22,9,31,5,13
8,7,9,22,31,5,13
8,7,9,22,5,31,13
8,7,9,22,5,13,31
7,8,9,22,5,13,31
7,8,9,5,22,13,31
7,8,9,5,13,22,31
7,8,5,9,13,22,31
7,5,8,9,13,22,31
5,7,8,9,13,22,31
Q7: Which one of the following in-place sorting algorithms needs the minimum number of swaps? (2017)
(a) Insertion Sort
(b) Quick Sort
(c) Heap Sort
(d) Selection Sort
Ans: (d)
Sol: Selection Sort is best sorting algorithm in terms of minimum no. of swap = O(n)
Q8: Algorithm design technique used in quicksort algorithm is? (2016)
(a) Dynamic programming
(b) Backtracking
(c) Divide and conquer
(d) Greedy method
Ans: (c)
Sol: It is one of the efficient algorithms in Divide and Conquer strategy.
Q9: Assume that the algorithms considered here sort the input sequences in ascending order.
If the input is already in ascending order, which of the following are TRUE? (2016 SET-2)
I. Quick sort runs in Θ(n2) time
II. Bubble sort runs in Θ(n2) time
III. Merge sort runs in Θ(n) time
IV. Insertion sort runs in Θ(n) time
(a) I and II only
(b) I and III only
(c) II and IV only
(d) I and IV only
Ans: (d)
Sol: I. Quicksort takes Θ(n2) in case of already sorted input. This is true
II. This is false. If no swap happens then bubble sort can stop in single loop. Θ(n) is best case. This is false!
III. Merge sort never takes more than Θ(n log n) This is false
IV. This is true. Insertion sort will finish in Θ(n) time in case of sorted input.
Answer D. I and IV.
Q10: The worst case running times of Insertion sort, Merge sort and Quick sort, respectively, are: (2016 SET-1)
(a) Θ(n logn), Θ(n logn), and Θ(n2)
(b) Θ(n2), Θ(n2), and Θ(nlogn)
(c) Θ(n2), Θ(nlogn), and Θ(nlogn)
(d) Θ(n2), Θ(nlogn), and Θ(n2)
Ans: (d)
Sol: Insertion sort: = Θ(n2)
Merge sort: = Θ(n log n)
Quick sort: = Θ(n2)
Note: here Θ is not average case since question asked worst case so Θ represent worst case only.
Q11: If one uses straight two-way merge sort algorithm to sort the following elements in ascending order:
20, 47, 15, 8, 9, 4, 40, 30, 12, 17
then the order of these elements after second pass of the algorithm is: (2015)
(a) 8, 9, 15, 20, 47, 4, 12, 17, 30, 40
(b) 8, 15, 20, 47, 4, 9, 30, 40, 12, 17
(c) 15, 20, 47, 4, 8, 9, 12, 30, 40, 17
(d) 4, 8, 9, 15, 20, 47, 12, 17, 30, 40
Ans: (b)
Sol: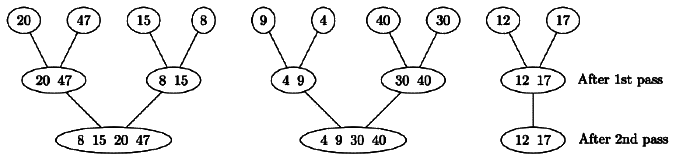
The answer is B.
Q12: A machine needs a minimum of 100 sec to sort 1000 names by quick sort. The minimum time needed to sort 100 names will be approximately (2015)
(a) 50.2 sec
(b) 6.7 sec
(c) 72.7 sec
(d) 11.2 sec
Ans: (b)
Sol: Running time of quick sort = c n lg n
For n = 1000, we get
100 = c * 1000 * lg 1000 => c = 0.01
So, for n = 100, we get running time = 0.01 * 100 * lg 100 = 6.7
Q13: Assume that a merge sort algorithm in the worst case takes 30 seconds for an input of size 64. Which of the following most closely approximates the maximum input size of a problem that can be solved in 6 minutes? (2015 SET-3)
(a) 256
(b) 512
(c) 1024
(d) 2048
Ans: (b)
Sol: The worst case time complexity of Merge sort is k x n log n for an input of size n.
For an input of size 64, the algorithm takes 30s. Therefore,
k x 64 log2 64 = 30s
k x 384 = 30s
⇒ k = 0.078125s
Let the size of the problem that can be solved in 6 minutes be x. Then,
k * x log2 x = 360s
From this, we get: x log2 x = 360s/0.078125s
⇒ x = 512
Q14: Suppose you are provided with the following function declaration in the C programming language.
int partition(int a[], int n);
The function treats the first element of a[] as a pivot, and rearranges the array so that all elements less than or equal to the pivot is in the left part of the array, and all elements greater than the pivot is in the right part. In addition, it moves the pivot so that the pivot is the last element of the left part. The return value is the number of elements in the left part. The following partially given function in the C programming language is used to find the kth smallest element in an array a[] of size n using the partition function. We assume k ≤ n 
The missing argument lists are respectively (2015 SET-2)
(a) (a, left_end, k) and (a+left_end+1, n-left_end-1, k-left_end-1)
(b) (a, left_end, k) and (a, n-left_end-1, k-left_end-1)
(c) (a+left_end+1, n-left_end-1, k-left_end-1) and (a, left_end, k)
(d) (a, n-left_end-1, k-left_end-1) and (a, left_end, k)
Ans: (a)
Sol: We have to find the kth smallest element.
if (left_end+1 > k)
If the above condition is true, it means we have kth smallest element on the left array, whose size is left_end Instead of n for the original array. (The "+1" is used because array index in C language starts from 0). So, we can do a recursive call as
- kth_smallest (a, left_end, k);
If the above condition is false, and left_end +1 ≠ k, it means kth smallest element is on the right part of the array and
it will be (k - left_end - 1)th element there as left_end+1 elements are gone in the left part.
So, the recursive call will be
kth_smallest(a + left_end + 1, n - left_end - 1, k - left_end - 1);
Correct Option: A.
Q15: Which one of the following is the recurrence equation for the worst case time complexity of the Quicksort algorithm for sorting n (≥2) numbers? In the recurrence equations given in the options below, c is a constant. (2015 SET-1)
(a) T(n)=2T(n/2)+cn
(b) T(n)=T(n-1)+T(1)+cn
(c) T(n)=2T(n-1)+cn
(d) T(n)=T(n/2)+cn
Ans: (b)
Sol: Quick sort worst case time complexity is n2, when the array is sorted or almost sorted then Quicksort algorithm runs in O(n2) time.
The recurrence relation for Quick sort worst case time complexity is
T(n) = T(n-1) + T(1) + cn.
Hence, B is Answer.
Q16: Consider the following sorting algorithms.
I. Quicksort
II. Heapsort
III> Mergesort
Which of them perform in least time in the worst case? (2014)
(a) I and II only
(b) II and III only
(c) III only
(d) I, II and III
Ans: (b)
Sol: Worst time complexity of Quicksort = O(n2)
Worst time complexity of Heapsort = O(nLogn)
Worst time complexity of Mergesort =O(nLogn)
Hence, Option(B) II and III.
Q17: You have an array of n elements. Suppose you implement quick sort by always choosing the central element of the array as the pivot. Then the tightest upper bound for the worst case performance is (2014 SET-3)
(a) O(n2)
(b) O(nlogn)
(c) θ(nlogn)
(d) O(n3)
Ans: (a)
Sol: When we choose the first element as the pivot, the worst case of quick sort comes if the input is sorted- either in ascending or descending order. Now, when we choose the middle element as pivot, sorted input no longer gives worst case behavior. But, there will be some permutation of the input numbers which will be giving the same worst case behavior. For example,
1234567
This array gives worst case behavior for quick sort when the first element is pivot.
6421357
This array gives the worst case behavior of O(n2) if we take middle element as the pivot- each split will be 1 element on one side and n - 1 elements on other side. Similarly, for any input, we can have a permutation where the behavior is like this. So, whichever element we take as pivot it gives worst case complexity of O(n2) as long as pivot is from a fixed position (not random position as in randomized quick sort).
Q18: Let P be a quick sort program to sort numbers in ascending order using the first element as the pivot. Let t1 and t2 be the number of comparisons made by P for the inputs [1 2 3 4 5] and [4 1 5 3 2] respectively. Which one of the following holds (2014 SET-1)
(a) t1 = 5
(b) t1 < to
(c) t1 > t2
(d) t1 = t2
Ans: (c)
Sol: it would be t1 t2, because the first case is the worst case of quicksort i.e. minimum number is chosen as pivot. Hence in the worst case the comparisons are high. The splitting occurs as
[1][2345]
[2] [345]
[3] [45]
[4] [5]
and
[123][45]
[1][23][4][5]
[2][3]
Number of recursive calls remain the same, but in second case the number of elements passed for the
recursive call is less and hence the number of comparisons also less.
Correct Answer: C
Q19: Which of the following sorting algorithms has the minimum running time complexity in the best and average case? (2013)
(a) Insertion sort, Quick sort
(b) Quick sort, Quick sort
(c) Quick sort, Insertion sort
(d) Insertion sort, Insertion sort
Ans: (a)
Sol: Insertion sort best case O(n)
Quick sort avg case O(n log n)
Ans (A)
Q20: The number of elements that can be sorted in Θ(logn) time using heap sort is (2013)
(a) Θ(1)
(b) Θ(√logn)
(c) Θ(logn/loglogn)
(d) Θ(logn)
Ans: (c)
Sol: To sort k elements in a heap, complexity is (k log k). Lets assume there are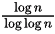 elements in the heap.
elements in the heap.
Complexity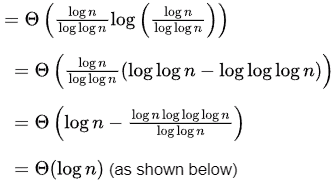
So, (C) is the answer.
log log n > log log log n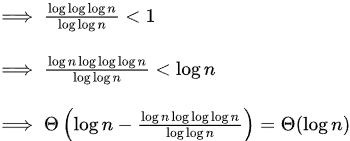
Q21: Which one of the following is the tightest upper bound that represents the number of swaps required to sort n numbers using selection sort? (2013)
(a) O(log n)
(b) O(n)
(c) O(n log n)
(d) O(n2)
Ans: (b)
Sol: In selection max you can do is n swaps.. selecting the smallest element from all the elements and replacing it correct position so O(n).
Q22: A list of n strings, each of length n, is sorted into lexicographic order using the merge-sort algorithm. The worst case running time of this computation is (2012)
(a) O (n log n)
(b) O(n2logn)
(c) O (n2 + logn)
(d) O (n2)
Ans: (b)
Sol: We are given the first character of each n strings. To sort them, it will take O(n log n) time. In the worst case we may have to do the above process 2 times, 3 times,..., n times. So,
n* O(n log n) = O(n2log n).
Q23: Which of the following algorithm design technique is used in merge sort? (2011)
(a) Greedy method
(b) Backtracking
(c) Dynamic programming
(d) Divide and Conquer
Ans: (d)
Sol: In Merge Sort we are keep on deviding the Array (can be any other Data Structure) into individual element.
Then Applying Merge Operation subsequently.
Then keeping on Combining the Solution.
So, Merge Sort Uses Divide & Conquer Method.
Hence, Option D is Ans.
Q24: Which one of the following in place sorting algorithms needs the minimum number of swaps? (2011)
(a) Quick sort
(b) Insertion sort
(c) Selection sort
(d) Heap sort
Ans: (c)
Sol: Correct Option: C - Selection sort.
Because in selection the maximum swaps which can take place are O(n)
Because we pick up an element an find the minimum (in case of forward sorting) from the next index till the end of array and than perform the swap
Hence, O(n) whereas in all other algos the swaps are greater (considering Worst-Case scenario)
Q25: In quick sort, for sorting n elements, the (n/4)th smallest element is selected as pivot using an O(n) time algorithm. What is the worst case time complexity of the quick sort? (2009)
(a) θ(n)
(b) θ(nlogn)
(c) θ(n2)
(d) θ(n2logn)
Ans: (b)
Sol: T(n) = O(n) pivot selection time +T(n/4 - 1) + T(3n/4)
which'll give θ(n log n).
Pivot selection complexity is given in questions. Pivot being the (n/4)th smallest element, once it is found,
we have two sub arrays- one of size (n/4 - 1) and other of size (3n/4) and for both of these we solve recursively.
Q26: What is the number of swaps required to sort n elements using selection sort, in the worst case? (2009)
(a) θ(n)
(b) θ(nlogn)
(c) θ(n2)
(d) θ(n2logn)
Ans: (a)
Sol: The answer is A.
In worst case, we have 1 swap in each loop except the last one and hence n - 1 swaps at max for 1 to n. Therefore the worst case number of swaps is Θ(n)
Q27: How many comparisons are needed to sort an array of length 5 if a straight selection sort is used and array is already in the opposite order? (2008)
(a) 1
(B) 10
(c) 15
(d) 20
Ans: (b)
Sol: Selection sort is not difficult to analyze compared to other sorting algorithms since none of the loops depend on the data in the array. Selecting the lowest element requires scanning all nelements (this takes n − 1 comparisons) and then swapping it into the first position. Finding the next lowest element requires scanning the remaining n − 1 elements and so on,
for (n − 1) + (n − 2) + ... + 2 + 1 = n(n − 1) / 2 ∈ Θ(n2) comparisons.
So whatever order they are arranged the number of comparisons will be sum of n-1 terms.
Here n=5
So total comparisons= 4*(4+1)/2=10.
Q28: If we use Radix Sort to sort n integers in the range (nk/2, nK), for some k>0 which is independent of n, the time taken would be? (2008)
(a) Θ(n)
(b) Θ(kn)
(c) Θ(n log n
(d) Θ(n2)
Ans: (c)
Sol: The complexity of Radix Sort is O(wn), for n keys which are integers of word size w.
Here, w = log2(nk) = k x log2(n)
So, the complexity is O(wn) = O(k x log2(n) x n), which leads to option C.
Q29: Consider the Quicksort algorithm. Suppose there is a procedure for finding a pivot element which splits the list into two sub-lists each of which contains at least one-fifth of the elements. Let T(n) be the number of comparisons required to sort n elements. Then (2008)
(a) T(n) ≤ 2T(n/5) + n
(b) T(n) ≤ T(n/5) + T(4n/5) + n
(c)T(n) ≤ 2T(4n/5) + n
(d) T(n) ≤ 2T(n/2) + n
Ans: (b)
Sol: T(n) ≤ T(n/5) + T(4n/5) + n
One part contains n/5 elements and the other part contains 4n/5 elements +n is common to all options, so
we need not to worry about it.
Hence, the answer is option B.
Q30: The average case and worst case complexities for Merge sort algorithm are (2007)
(a) O(n2), O(n2)
(b) O(n2), O(n log2 n)
(c) O(n log2 n), O(n2)
(d) O(n log2 n), O(n log2 n)
Ans: (d)
Sol: both are O(nlog2n)
Q31: Selection sort algorithm design technique is an example of (2007)
(a) Greedy method
(b) Divide-and-conquer
(c) Dynamic Programming
(d) Backtracking
Ans: (a)
Sol: Correct Answer would be A) Greedy Algorithm
Because, In the first iteration we put a pointer in the start of the array. Then next we start searching index of minimum element index in the rest of the array. Then replace the starting pointer value with minimum index value. (Considering the we are sorting in ascending order). Then repeat this process for each element.
Q32: Which of the following sorting algorithms has the lowest worst-case complexity? (2007)
(a) Merge sort
(b) Bubble sort
(c) Quick sort
(d) Selection sort
Ans: (a)
Sol: Irrespective of the input, merge sort always have a time complexity of Θ(n log n)
Q33: The median of n elements can be found in O(n) time. Which one of the following is correct about the complexity of quick sort, in which median is selected as pivot? (2006)
(a) θ(n)
(b) θ(nlogn)
(c) θ(n2)
(d) θ(n3)
Ans: (b)
Sol: When we choose the median as the pivot element, we guarantee the split in half, so the best case of quick sort.
T(n) = 2T(n/2) + O(n) = O(n log n)
Q34: Which one the following in place sorting algorithms needs the minimum number of swaps? (2006)
(a) Quick-sort
(b) Insertion sort
(c) Selection sort
(d) Heap sort
Ans: (c)
Sol: Because in selection the maximum swaps which can take place are O(n)
Because we pick up an element an find the minimum (in case of forward sorting) from the next index till the end of array and than perform the swap
Hence, O(n) whereas in all other algos the swaps are greater (considering Worst-Case scenario)
Q35: The tightest lower bound on the number of comparisons, in the worst case, for comparison-based sorting is of the order of (2004)
(a) n
(b) n2
(c) nlogn
(d) nlog2n
Ans: (c)
Sol: For comparison-based sorting the asymptotically tight bound for worst case is given by Θ(n log n), which means it is the tightest upper bound (big O) as well as the tightest lower bound (big omega). So, answer is n log n.
Tightest lower bound of sorting (say S(n)) is means there is no function f which has an order of growth larger than n log n and f(n) = Ω(S(n)) holds.
A usual mistake is to think worst case changes with lower and upper bounds, but that is not the case. Worst case is defined for the algorithm and it is always the input which causes the algorithm the maximum complexity.
Correct Answer: C
Q36: In a permutation a1.....an of n distinct integers, an inversion is a pair (ai, aj) such that i < j and ai > aj.
What would be the worst case time complexity of the insertion Sort algorithm, if the inputs are restricted to permutations of 1....n with at most n inversions? (2003)
(a) Θ(n2)
(b) Θ(nlogn)
(c) Θ(n1.5)
(d) Θ(n)
Ans: (d)
Sol: As the question says, how the Inversion is defined.
In a permutation a1... an, of n distinct integers, an inversion is a pair (ai, aj) such that i < j and ai > aj.
- One important thing to see is Difference between swap and Inversions.
- Swapping is done explicitly by the programmer, hence a explicit feature whereas, Inversion is an implicit feature which is defined in the input.
Ex:- Take the input => {0, 1, 9, 8, 10, 7, 6, 11}
How many Inversions here: {9,8}, {9,7}, {9,6},{8,7},{8,6}, {10,7}, {10,6} and {7,6}.
Hence, it is an implicit feature of the input and not any explicit operation done (Swap).
Actual Time complexity of Insertion Sort is defined as (N + f(N)), where f (N) is the total number of Inversions.
Ex:- Again take the input => {0, 6, 7, 8, 9, 10, 1}
Here, how many comparisons will be there to place 1 in the right place ?
- First of all, 1 is compared with 10 - Returns True as it is smaller than 10.
- Then, with 9 - again True.
- Similar, happens with 6, 7, 8 - All return True.
Hence, There 5 comparisons were the Inversions and 1 more comparison will be there, in which outer while loop fails.
For, placing 1 in the right place 6 comparisons are there.
Hence, Total Comparisons in the Insertion sort will be :- Total number of elements for which our while loop fails + Total number of inversions in the input
- Total number of elements for which our while loop fails :- Suppose the input {0, 6, 7, 8, 9, 10, 1}. Here, first 0 will be kept as it is and one while loop fail comparison for each element, hence total comparisons like this: (N - 1) = O (N)
- Total number of inversions in the input :- Best Case: 0 and in the Worst Case: N(N - 1)/2= O (N2)
Total Time complexity of insertion sort: Θ(N + f(N))
It is given here that at most N inversions are there, so we get the best Time complexity :-
Θ(N + f(N)) = Θ(Ν + Ν) = Θ(Ν)
Q37: The usual Θ(n2) implementation of Insertion Sort to sort ab array uses linear search to identify the position where an element is to be inserted into the already sorted part of the array. If, instead, we use binary search to identify the position, the worst case running time will (2003)
(a) remain Θ(n2)
(b) become Θ(n(logn)2)
(c) become Θ(nlogn)
(d) become Θ(n)
Ans: (a)
Sol: In insertion sort, with linear search, it takes
(worst case) n comparisons for searching the right position, and n swaps to make room to place the element.
Hence for n elements, a total of n x (n + n); n for search and n for swaps.
= Θ(2n2) = Θ(n2)
If we replace it with binary search, it takes
(worst case) log n comparisons for searching the right position, and n swaps to make room to place the element.
Hence for n elements, a total of n x (log n + n); n for search and n for swaps.
= Θ(n × log n + n2) = Θ(n2)
Hence, answer is A.
Q38: If one uses straight two-way merge sort algorithm to sort the following elements in ascending order:
20, 47, 15, 8, 9, 4, 40, 30, 12, 17
then the order of these elements after second pass of the algorithm is: (1999)
(a) 8, 9, 15, 20, 47, 4, 12, 17, 30, 40
(b) 8, 15, 20, 47, 4, 9, 30, 40, 12, 17
(c) 15, 20, 47, 4, 8, 9, 12, 30, 40, 17
(d) 4, 8, 9, 15, 20, 47, 12, 17, 30, 40
Ans: (b)
Sol: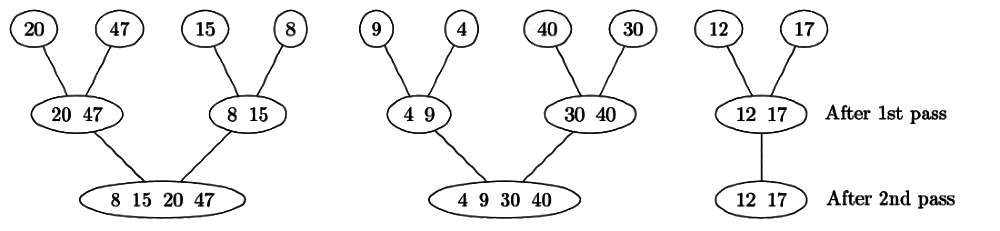 The answer is B.
The answer is B.
Q39: A sorting technique is called stable if (1999)
(a) it takes O(n log n) time
(b) it maintains the relative order of occurrence of non-distinct elements
(c) it uses divide and conquer paradigm
(d) it takes O(n) space
Ans: (b)
Sol: If it maintains the relative order of occurrence of non-distinct elements.
(from definition of stable sorting).
Q40: Give the correct matching for the following pairs: (1998)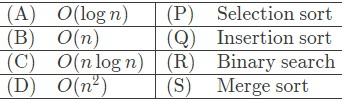
(a) A-R B-P C-Q D-S
(b) A-R B-P C-S D-Q
(c) A-P B-R C-S D-Q
(d) A-P B-S C-R D-Q
Ans: (b)
Sol: Here we are talking about the worst case time complexities of the given algorithms. Selection actually refers to selection algorithm and not selection sort.
- Selection: O(n)
- Insertion sort: O(n2)
- Binary search: O(log n)
- Merge sort: O(n log n)
A - R B - P C - S D - Q.
Correct Answer: B
Q41: Quick-sort is run on two inputs shown below to sort in ascending order taking first element as pivot
(i). 1, 2, 3, ... n
(ii). n, n - 1, n - 2,..., 2,1
Let C1 and C2 be the number of comparisons made for the inputs (i) and (ii) respectively. Then, (1996)
(a) C1 > C2
(b) C1 = C2
(c) C1 > C2
(d) we cannot say anything for arbitrary n
Ans: (b)
Sol: both are the worst cases of quick sort. (assuming pivot is either first or last element)
- is sorted in ascending order.
- is sorted in descending order.
Q42: Merge sort uses: (1995)
(a) Divide and conquer strategy
(b) Backtracking approach
(c) Heuristic search
(d) Greedy approach
Ans: (a)
Sol: One of the best examples of Divide and Conquer strategy.
Q43: Algorithm design technique used in quicksort algorithm is? (1994)
(a) Dynamic programming
(b) Backtracking
(c) Divide and conquer
(d) Greedy method
Ans: (c)
Sol: It is one of the efficient algorithms in Divide and Conquer strategy.
Q44: Randomized quicksort is an extension of quicksort where the pivot is chosen randomly.
What is the worst case complexity of sorting n numbers using randomized quicksort? (2001)
(a) O(n)
(b) O(nlogn)
(c) O(n2)
(d) O(n!)
Ans: (c)
Sol: There are two cases, when Randomized Quick Sort will result into worst case time complexity of O(n2)
- When all elements are same in the input array, Partition algorithm will divide input array in two sub-arrays, one with n - 1 elements and second with 0 element. There is an assumption here that, we are using the same partition algorithm without any modification.
- If the randomized pivot selector happens to select the smallest or largest element N times in a row, we will get the worst possible performance. Though the probability of this particular case is about 2n-1/n!.
PS: Option D is also correct here as n2 = O(n!) though (C) is a better choice.
Q45: Choose the correct alternatives (more than one may be correct) and write the corresponding letters only:
Following algorithm(s) can be used to sort n in the range [1...n3] in O(n) time (1992)
(a) Heap sort
(b) Quick sort
(c) Merge sort
(d) Radix sort
Ans: (d)
Sol: Although people have provided correct answers but it seems some more explanation is required.
Let there be d digits in max input integer, b is the base for representing input numbers and n is total numbers then Radix Sort takes O(d* (n + b)) time. Sorting is performed from least significant digit to most significant digit.
For example, for decimal system, b is 10. What is the value of d? If k is the maximum possible value, then d would be O(logb(k)). So overall time complexity is O((n + b) *logb(k)). Which looks more than the time complexity of comparison based sorting algorithms for a large k. Let us first limit k. Let k ≤ nc where c is a constant. In that case, the complexity becomes O(n logb(n)). But it still does not beat comparison based sorting algorithms.
What if we make value of b larger?. What should be the value of b to make the time complexity linear? If we set b as n then we will get the time complexity as O(n).
In other words, we can sort an array of integers with range from 1 to nc, If the numbers are represented in base n (or every digit takes log2(n) bits).
Q46: Choose the correct alternatives (More than one may be correct).
The complexity of comparison based sorting algorithms is: (1990)
(a) Θ(n log n)
(b) Θ(n)
(c) Θ(n2)
(d) Θ(n√n)
Ans: (a)
Sol: First of all which sorting algorithm is being asked? It is not just the normal ones we see in algorithm text books but can be any sorting algorithm which uses comparisons. So, in crux we cannot rely on any specific algorithms for this question.
Now, coming to the options, we can see that Θ notation is used. We use Θ notation for a problem when
- we have a lower bound for the solution -- that is any algorithm which solves the problem must have minimum this much complexity (time complexity being implied)
- there exist an algorithm which solves the problem with above minimum time complexity (worst case input being implied)
For comparison based sorting we already have known algorithms like heap sort and merge sort, which solves the problem in O(n log n) (See O) and now if we show that this is the best possible by any algorithm our answer becomes Θ(n log n).
And it is indeed proved that for comparison based sorting minimum Ω(n log n) comparisons are required and considering time taken being proportional to the number of comparisons, the time complexity is also Ω(n log n). Proof of this is given here but in essence it says
- The output of sorting n elements can be any of the n! permutations.
- Each comparison reduces the possibility by 2
- So, to finish all n! permutations we need minimum lg n! comparisons which is Ω(n lg n)
Now, if someone asks what is the minimum number of comparisons to sort 5 elements answer is definitely ≥ lg 5! ≥ lg 120 ≥ 7.
We can only use ≥ here and not = unless we prove that we can do it in 7 comparisons. But interestingly, this ≥ becomes = till n = 11 as given in below Wikipedia link.
Q47: Let P be a quicksort program to sort numbers in ascending order. Let t1 and t2 be the time taken by the program for the inputs [1 2 3 4] and [5 4 3 2 1], respectively. Which of the following holds? (1987)
(a) t1 = t2
(b) t1 > t2
(c) t1 < t2
(d) t1 = t2 + 5 log 5
Ans: (c)
Sol: Actually, in both the cases, it will take O(n2) time for partition algorithm and T(n - 1) time for subproblem.
As n is the number of inputs and in the 2nd case inputs are 5 (greater than 1st one that is 4), t1 < t2.
|
81 videos|113 docs|34 tests
|
FAQs on Previous Year Questions: Sorting - Algorithms - Computer Science Engineering (CSE)
| 1. What is sorting in computer science? |  |
| 2. What are the different types of sorting algorithms commonly used in programming? |  |
| 3. How does the Bubble Sort algorithm work? |  |
| 4. What is the time complexity of the Merge Sort algorithm? |  |
| 5. When should Quick Sort be preferred over Merge Sort? |  |





















