Previous Year Questions: Transaction | Database Management System (DBMS) - Computer Science Engineering (CSE) PDF Download
Q1: Which of the following statements about the Two Phase Locking (2PL) protocol is/are TRUE? (2024 SET 2)
(a) 2PL permits only serializable schedules
(b) With 2PL, a transaction always locks the data item being read or written just before every operation and always releases the lock just after the operation
(c) With 2PL, once a lock is released on any data item inside a transaction, no more locks on any data item can be obtained inside that transaction
(d) A deadlock is possible with 2PL
Ans: (a, c, d)
Sol: A. 2PL -> serial schedule
C. Also it's the property of 2pl which states that once a lock is released no further lock can be taken as the shrinking phase of the transaction starts and you can't acquire any lock in the shrinking phase of a transaction.
D. Deadlock can occur in 2PL as in a schedule 2 transaction can wait for each other to release the locks. This is the disadvantage of normal 2PL
Q2: Once the DBMS informs the user that a transaction has been successfully completed, its effect should persist even if the system crashes before all its changes are reflected on disk. This property is called (2024 SET 2)
(a) durability
(b) atomicity
(c) consistency
(d) isolation
Ans: (a)
Sol: From the definition of Durability, whenever a change happens in a successful transaction, it persists even if the system failures.
Therefore, the correct option is A
Q3: Consider the following read-write schedule S S over three transactions T1 , T2 , and T 3 , where the subscripts in the schedule indicate transaction IDs: (2024 SET 1)
S : r 1 ( z ) ; w 1 ( z ) ; r 2 ( x ) ; r 3 ( y ) ; w 3 ( y ) ; r 2 ( y ) ; w 2 ( x ) ; w 2 ( y )
Which of the following transaction schedules is/are conflict equivalent to S S ?
(a) T1T2T3
(b) T1T3T2
(c) T3T2T1
(d) T3T1T2
Ans: (b, c, d)
Sol: 

The corresponding polygraph for the given transaction. it has three conflict pairs as T 3 → T 2 as
r 3 ( y ) → w 2 ( y ) , w 3 ( y ) → r 2 ( y ) , w 3 ( y ) → w 2 ( y ) .
Because the graph is acyclic it is conflict serializable schedule and its corresponding conflict equal schedule is based on the topological order of the given graph.
Therefore following are possible serial schedules:
- T1, T3, T2
- T3, T1, T2
- T3, T2, T1
Option (B, C, D) are correct.
Q4: Let R i ( z ) R i (z) and W i denote read and write operations on a data element z z by a transaction T i , respectively. Consider the schedule S with four transactions. (2022)
S: R4 (x) R2(x) R3 (x) R1 (y) W1 (y) W2 (x)W3 (y) R4 (y)
Which one of the following serial schedules is conflict equivalent to S?
(a) T1→T3→T4→T2
(b) T1→T4→T3→T2
(c) T4→T1→T3→T2
(d) T3→T1→T4→T2
Ans: (a)
Sol: Conflict operations:
i. Transaction T i reading data item K, after that Transaction T j writing data item K
ii. Transaction T i writing data item K, after that Transaction T j reading data item K
iii. Transaction T i writing data item K, after that Transaction T j writing data item K.
Note that, Transaction T i writing data item ‘K’, after that Transaction T j writing data item ‘P’ are not conflict operations due to those are different data items.
Tabular representation of given schedule is :
If you observe,
- Line 1 and Line 6 are conflict operations. So in Serial schedule Transaction T4 must be before T2
- Line 3 and Line 6 are conflict operations. So in Serial schedule Transaction T3 must be before T2
- Line 4 and Line 7 are conflict operations. So in Serial schedule Transaction T1 must be before T3
- Line 5 and Line 8 are conflict operations. So in Serial schedule Transaction T1 must be before T4
- Line 7 and Line 8 are conflict operations. So in Serial schedule Transaction T3 must be before T4
Accumulating all these points and running Topological sort, T1 should be first followed by T3 , T4 and T2 in order.
Q5: Let S be the following schedule of operations of three transactions T1 , T2 and T3 in a relational database system: (2021 SET 2 )
R2(Y), R1 (X), R3(Z), R1 (Y) W1 (X), R2(Z), W2 (Y), R3(X), W3(Z)
Consider the statements P and Q below:
P: S is conflict-serializable.
Q: If T3 commits before T1 finishes, then S is recoverable.
Which one of the following choices is correct?
(a) Both P and Q are true
(b) P is true and Q is false
(c) P is false and Q is true
(d) Both P and Q are false
Ans: (b)
Sol:
 T1 → T2 due to R1 (Y) being before W2 (Y)
T1 → T2 due to R1 (Y) being before W2 (Y) - T1 → T3 due to W1 (X) being before R3(X)
- T2 → T3 due to R2(Z) is being W3(Z) in the schedule.
There are no other conflicts and the discovered conflicts are not
Therefore, the given schedule is Conflict Serializable.
Statement Q : If T3 commits, before T1 finishes, then S is recoverable.
Q6: Let r i (z) and w i ( z ) denote read and write operations respectively on a data item z by a transaction T i . Consider the following two schedules. (2021SET 1 )
S 1 : r 1 (x) r1 (y) r2 (x) r2 (y) w2 (y) w1 (x)
S2:r1 (x)r2 (x)r2 (y) w2 (y) r1 (y) w1 (x)
Which one of the following options is correct?
(a) S1 is conflict serializable, and S2 is not conflict serializable
(b) S1 is not conflict serializable, and S2 is conflict serializable
(c) Both S1 and S2 are conflict serializable
(d) Niether S1 nor S2 is conflict serializable
Ans: (b)
Sol:

Here r1 ( y ) and w2 ( y ) are conflicting pairs, giving T 1 → T 2 and r2 ( x ) and w1 ( x ) giving T 2 → T 1 , so the schedule is not conflict serializable.

Here r2 ( x ) and w1 ( x ) are conflicting pairs giving T 2 → T 1 , and w2 ( y ) and r1 ( y ) also giving T2 → T1 , therefore this schedule is conflict serializable.
Correct Option B
Q7: Suppose a database system crashes again while recovering from a previous crash. Assume checkpointing is not done by the database either during the transactions or during recovery. (2021 SET1 )
Which of the following statements is/are correct?
(a) The same undo and redo list will be used while recovering again
(b) The system cannot recover any further
(c) All the transactions that are already undone and redone will not be recovered again
(d )The database will become inconsistent
Ans: (a)
Sol: Ideation/Source of the content: Navathe 6th Edition, 22.1: Recovery Concepts
Support for option A and against option C: Since check-pointing is not used we have to depend on the system logs. Let's suppose we have three transactions A, B and C. Also assume that transaction A and C commits before failure and B was started but the system crashed before it can commit. So, in the first recovery process database will redo A and C as per the system logs. Now consider that while redoing A successfully commits, the system crashed for the second time before the B can commit. So, while recovering for the second time the same system logs will be used. However, it is should be noted that the system logs will also have entry to redo transaction A since it was committed after the first failure. However, the undo/redo operations are idempotent (they are the same no matter how many time they are executed).
Against option B: If the system crashes again same logic as above can be used for recovery.
Against option D: Inconsistency refers to situations (generally) when the value of a shared variable varies in two or more transactions, but that doesn’t seem to happen here as no uncommitted transaction’s data is being read/written during the entire recovery process.
Conclusion: So, the only option of selecting the same list for undo/redo seems to be correct.
Q8: Consider a schedule of transactions T1 and T2: (2020)
Here, RX stands for "Read(X)" and WX stands for "Write(X)". Which one of the following schedules is conflict equivalent to the above schedule?

(A) a
(B) b
(C) c
(D) d
Ans: (a)
Sol: If you draw the dependency graph, you'll notice that there is a cycle. Hence Option (D) and Option (B) are straightaway False.
Now in Option (C), there is a swapping operation of conflicting operations W1 (D) and R2 (D) . Hence it's False as well.
Hence, Option(A) is the answer
Q9: Consider the following two statements about database transaction schedules: (2019)
I. Strict two-phase locking protocol generates conflict serializable schedules that are also recoverable.
II. Timestamp-ordering concurrency control protocol with Thomas' Write Rule can generate view serializable schedules that are not conflict serializable.
Which of the above statements is/are TRUE?
(a) I only
(b) II only
(c) Both I and II
(d) Neither I nor II
Ans: (c)
Sol:
- Strict 2PL allows only schedules whose precedence graph is acyclic i.e. schedule is Conflict Serial. In strict 2PL , transactions do not release exclusive locks until the transaction has committed or aborted i.e. schedule is recoverable.
- Time stamp ordering schedule with Thomas write rule generate View serial schedule with BLIND WRITE. Because of BLIND WRITE it won't be Conflict Serial.
So, Option C - both are true
Q10: Two transactions T 1 a n d T 2 are given as: (2017 SET 2)
T 1 : r1 ( X ) w1 ( X ) r1 ( Y ) w1 ( Y )
T 2 : r2 ( Y ) w2 ( Y ) r2 ( Z ) w2 ( Z )
where ri ( V )denotes a read operation by transaction Ti on a variable V and w i ( V ) denotes a write operations by transaction Ti on a variable V. The total number of conflict serializable schedules that can be formed by T1 a n d T2 is
(a) 53
(b) 54
(c) 70
(d) 12
Ans: (b)
Sol: There is only one way to have (conflict) serializable schedule as T 1 → T 2 ,
because last operation of T 1 and first operation of T 2 conflicts with each other.
Now See How many schedules are conflict serializable to T 2 → T 1 .
I am writing T 1 −
R ( A ) W ( A ) R ( B ) W ( B )
If you notice, I wrote T 1 with space in between operation. Now See T 2 from right, if we see T 2 from right, then tell me first operation of T 2 that conflicts with any operation of T 1 .
W ( C ) and R ( C ) do not have any conflict with any operation, but W ( B ) has.
Pick W ( B ) and see, at how many places it can be there.
Case1: W ( B ) R ( A ) W ( A ) R ( B ) W ( B )
Case2: R ( A ) W ( B ) W ( A ) R ( B ) W ( B )
Case3: R ( A ) W ( A ) W ( B ) R ( B ) W ( B )
Pick each case and see, how many positions other operation of T 2 can take.
Case1: W ( B ) R ( A ) W ( A ) R ( B ) W ( B )
How many positions W ( C ) and R ( C ) can take ?
(note that these W ( C ) and R ( C ) cant come before W ( B ) )
that is 5 C 1 + 5 C 2 = 15 (either both can take same space or two different spaces)
Now see, for each of these 15 positions, how many can R ( B ) take ?
Obviously, W ( B ) cant come before R ( B ) , therefore one position.
15 × 1 = 15 total possible schedules from case 1.
Case2: R ( A ) W ( B ) W ( A ) R ( B ) W ( B )
How many positions W ( C ) and R ( C ) can take ?
that is 4 C 1 + 4 C 2 = 10 (either both can take same space or two different spaces)
Now see, for each of these 10 positions, how many can R ( B ) take ?
Only 2 positions, because it has to come before W ( B ) .
10 × 2 = 20 total possible schedules from case 2.
Case3: R ( A ) W ( A ) W ( B ) R ( B ) W ( B )
How many positions W ( C ) and R ( C ) can take ?
that is 3 C 1 + 3 C 2 = 6
Now see, for each of these 6 positions, how many can R ( B ) take ?
Only 3 positions, because it has to come before W ( B ) .
6 × 3 = 18 total possible schedules from case 3.
total schedules that are conflict serializable as T 2 → T 1 = 15 + 20 + 18 = 53.
total schedules that are conflict serializable as T 1 → T 2 = 1. total schedules that are conflict serializable as either T 2 → T 1 or T 1 → T 2 = 53 + 1 = 54 .
Q11: In a database system, unique time stamps are assigned to each transaction using Lamport's logical clock . Let TS( T1 ) and TS( T2 ) be the timestamps of transactions T1 and T2 respectively. Besides, T1 holds a lock on the resource R, and T2 has requested a conflicting lock on the same resource R. The following algorithm is used to prevent deadlocks in the database system assuming that a killed transaction is restarted with the same timestamp. (2017 SET 1)

Assume any transactions that is not killed terminates eventually. Which of the following is TRUE about the database system that uses the above algorithm to prevent deadlocks?
(a) The database system is both deadlock-free and starvation- free.
(b) The database system is deadlock- free, but not starvation-free.
(c) The database system is starvation-free but not deadlock- free.
(d) The database system is neither deadlock- free nor starvation-free.
Ans: (a)
Sol: In a database system, unique timestamps are assigned to each transaction using Lamport's logical clock
Since Unique Timestamps are assigned, so there is no question of two transaction having same timestamp.
Moreover, there is nothing mentioned about the size of the counter by which it can be determined that whether there will be case of timestamp wrap around or not.
So, there will be no timestamp wrap around.
In Lamport's logical clock Timestamps are assigned in increasing order of enumeration.
So, Ti < Tj if Transaction Ti came into system before Tj .
The above scheme given is nothing but " Wound-Wait " Scheme in which younger transaction is killed by older transaction that came into system before this younger transaction came. [1] ]2]
So, this is a part of Basic Time-Stamp Ordering in Concurrency Control.
And Basic Time Stamp ordering protocol is deadlock free and not starvation free, in general.
Here in this question according to given condition, the database system is both deadlock free and starvation free as well , as it is Wound wait scheme and in case of wound wait it avoid starvation, because in Wound Wait scheme we restart a transaction that has been aborted, with it's same original Timestamp . If it restart with a new Timestamp then there is a possibility of Starvation ( as larger TimeStamp transaction is aborted here and new Transaction which is coming next have always greater TimeStamp than previous one ). But that is Not the case here.
Q12: Consider the following databases chedule with two transactions, T1 and T2. (2016 set 2)
S = r2 ( X ) ; r1 ( X ) ; r2 ( Y ) ; w1 ( X ) ; r1 ( Y ) ; w2 ( X ) ; a 1 ; a 2
where r i ( Z )denotes a read operation by transaction T i on available Z, w i ( Z ) denotes a write operation by T i on
available Z and a i denotes an abort by transaction Ti .
Which one of the following statements about the above schedule is TRUE?
(a) S is non-recoverable
(b) S is recoverable,but has a cascading abort
(c) S does not have a cascading abort
(d) S is strict
Ans: (c)
Sol:
(A): This is not possible, because we have no dirty read ! No dirty read ⟹Recoverable
(B): This is not possible, because of no Dirty read ! No dirty read ⟹No cascading aborts !
(D): This is not true, because we can see clearly in image that after W1(X) before T1 commit or aborts T2 does W2(x) !
C is only option remaining !
Q13: Suppose a database schedule S involves transactions T1,...,Tn. Construct the precedence graph of S with vertices representing the transactions and edges representing the conflicts. If S is serializable, which one of the following orderings of the vertices of the precedence graph is guaranteed to yield a serial schedule? (2016 set 2)
(a) Topological order
(b) Depth-first order
(c) Breadth-first order
(d) Ascending orderoftransactionindices
Ans: (a)
Sol: Now S can be either Conflict serializable or Can be view Serializable but Not conflict serializable.
Take an example of below schedule

The precedence graph of above will be cyclic and the above schedule is not Conflict serializable , but View serializable as T2->T1 and hence SERIALIZABLE.
So, clearly my topological sort algorithm would fail on such a precedence graph.
DFS algorithm would only tell about the nature of precedence graph( Like whether it has cycle or not, ancestor-descendants relationship) and this has nothing to do with serializability. Similarly for BFS.
Option (D) is clearly non-sense
Now if I am able to produce a Topological order of a precedence graph, that means the graph is Acyclic and hence the schedule S will be conflict equal to the serial schedule order given by topological order. A conflict equivalent schedule is also view equivalent and hence serializable.
Answer (A).
Q14: Consider the following two phase locking protocol. Suppose a transaction T accesses (for read or write operations), a certain set of objects {O1,... ,Ok}. This is done in the following manner: (2016 SET1)
Step 1. T acquires exclusive locks to O1,...,Ok in increasing order of their addresses.
Step 2. The required operations are performed.
Step 3. All locks are released.
This protocol will
(a) guarantee serializability and deadlock-freedom
(b) guarantee neither serializability nor deadlock-freedom
(c) guarantee serializability but not deadlock-freedom
(d )guarantee deadlock-freedom but not serializability
Ans: (a)
Sol: Two Phase Locking protocol is conflict serializable. So this is a modified version of the basic 2 P L protocol, So serializabilty should be guaranteed.. and we can get a serializable scheduling by ordering based on Lock points(same as in basic 2 P L )..
Now in Step 1 , exclusive locks are aquired to O 1 , O 2 , O 3 .... in increasing order of addresses .. since it is mentioned as exclusive lock, only one transaction can lock the object..
Due to acquiring of locks based on ordering of addresses.. and locks aren't released until the transaction completes its operation.. we can prevent the circular wait condition, and hence making it deadlock free.
So, the answer should be (A) guarantees serializability and deadlock freedom
Q15: Which one of the following is NOT a part of the ACID properties of database transactions? (2016 SET 1)
(a) Atomicity
(b) Consistency
(c) Isolation
(d) Deadlock-freedom
Ans: (d)
Sol: A - Atomicity
C - Consistency
I - Isolation
D - Durability.
Answer (D)
Q16: Consider the following partial Schedule S involving two transactions T1 and T2. Only the read and the write operations have been shown. The read operation on data item P is denoted by read(P) and the write operation on data item P is denoted by write(P). (2015 SET 3)
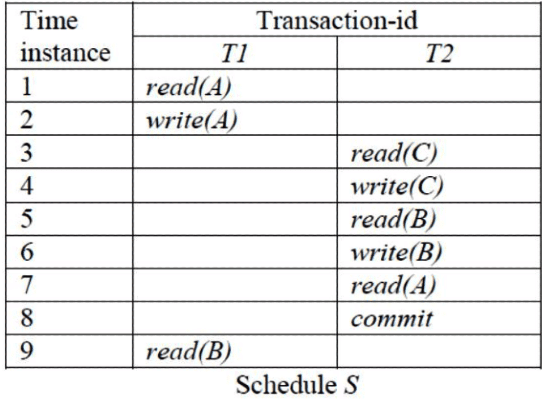
Suppose that the transaction T1 fails immediately after time instance 9. Which one of the following statements is correct?
(a) T2 must be aborted and then both T1 and T2 must be re-started to ensure transaction atomicity
(b) Schedule S is non-recoverable and cannot ensure transaction atomicity
(c) Only T2 must be aborted and then re-started to ensure transaction atomicity
(d) Schedule S is recoverable and can ensure atomicity and nothing else needs to be done
Ans: (b)
Sol: The correct option is B.
Why A is not correct because it says abort transaction T2 and then redo all the operations .
But is there a guarantee that it will succeed this time ??(no maybe again T1 will fail).
Now as to why b is correct because as the other answer points out it is by definition an irrecoverable schedule now even if we start to undo the actions on by one(after t1 fails) in order to ensure transaction atomicity. Still we cannot undo a committed transaction. Hence, this schedule is unrecoverable by definition and also not atomic since it leaves the data base in an inconsistent state.
Q17: Consider a simple checkpointing protocol and the following set of operations in the log. (2015 SET 2)
(start, T4); (write, T4, y, 2, 3); (start, T1); (commit, T4); (write, T1, z, 5, 7);
(checkpoint);
(start, T2); (write, T2, x, 1, 9); (commit, T2); (start, T3), (write, T3, z, 7, 2);
If a crash happens now and the system tries to recover using both undo and redo operations, what are the contents of the undo list and the redo list?
(a) Undo: T3, T1; Redo: T2
(b) Undo: T3, T1; Redo: T2, T4
(c) Undo: none; Redo: T2, T4, T3, T1
(d) Undo: T3, T1, T4; Redo: T2
Ans: (a)
Sol:
Now from the table we can find that T1 and T3 has uncommitted write operation, so they must be undone. Even though T2 has committed after writing, but it is after checkpoint. So, it needs to be redone.
Answer is A.
Q18: The constraint that the sum of the accounts x and y should remain constant is that of (2015 SET 2)
(a) Atomicity
(b) Consistency|
(c) Isolation
(d) Durability
Ans: (b)
Sol: B. Consistency
In the given transaction Atomicity guarantees that the said constraint is satisfied. But this constraint is not part of Atomicity property. It is just that Atomicity implies Consistency here.
Q19: Consider the transactions T1, T2, and T3 and the schedules S1 and S2 given below. (2014 SET 3)
T1 : r1(x); r1(Z) ; w1(x); w1(Z)
T2 : r2(x); r2(Z); w2(Z)
T3 : r3(x); r3(x); w3(Y)
S1: r1(x); r3(Y); r3(x); r2(Y); r2(Z); w3(Y); w2(Z); r1(Z); w1(x); w1(Z)
S2: r1(x); r3(Y); r2(Y); r3(x); r1(Z); r2(Z); w3(Y); w1(x); w2(Z); w1(Z)
Which one of the following statements about the schedules is TRUE?
(a) Only S1 is conflict-serializable
(b) Only S2 is conflict-serializable.
(c) Both S1 and S2 are conflict-serializable
(d) Neither S1 nor S2 is conflict-serializable
Ans: (a)
Sol: 
S1 has no cycle hence, Conflict-Serializable
S2 has cycle hence NOT Conflict-Serializable
Answer is option A.
Q20: Consider the following schedule S of transactions T1, T2, T3, T4: (2014 SET 2)
Which one of the following statements is CORRECT?
(a) S is conflict-serializable but not recoverable
(b) S is not conflict-serializable but is recoverable
(c) S is both conflict-serializable and recoverable
(d) S is neither conflict-serializable nor is it recoverable
Ans: (c)
Sol: Answer: S is both conflict serializable and recoverable.
Recoverable? Look if there are any dirty reads? Since there are no dirty read, it simply implies schedule is recoverable( if there were dirty read, then we would have taken into consideration the order in which transactions commit)
Conflict serializable? Draw the precedence graph( make edges if there is a conflict instruction among Ti and Tj. But for the given schedule, no cycle exists in precedence graph, thus it's conflict serializable.
Q21: Consider the following four schedules due to three transactions (indicted by the subscript) using read and write on a data item x, denoted by r(x) and w(x) respectively. Which one of them is conflict serializable? (2014 SET 1)
(a) r1(x); r2(x); w1(x); r3(x); w2(x)
(b) r2(x); r1(x); w2(x); r3(x); w1(x)
(c) r3(x); r2(x); r1(x); w2(x); w1(x)
(d )r2(x); w2(x); r3(x); r1(x); w1(x)
Ans: (d)
Sol: In option D, there is no interleaving of operations. The option D has first all operations of transaction 2, then 3 and finally 1 There can not be any conflict as it is a serial schedule with sequence 2 --> 3 -- > 1
Q22: Consider the following transactions with data items P and Q initialized to zero: (2012)

Any non-serial interleaving of T1 and T2 for concurrent execution leads to
(a) a serializable schedule
(b) a schedule that is not conflict serializable
(c) a conflict serializable schedule
(d )a schedule for which a precedence graph cannot be drawn
Ans: (b)
Sol: T1: r (P), r (Q), w (Q)T2: r (Q), r (P), w (P).
Now, consider any non serial schedule for example,
S : r1(P), r2(Q), r1(Q), r2(P), W1 (Q), W2(P).
Now, draw a precedence graph for this schedule. Here there is a conflict from
T1 → T2 and there is a conflict from T2 → T1 . Therefore, the graph will contain a cycle. So we can say that the schedule is not conflict serializable.
Q23: Consider the following schedule for transactions T1, T2 and T3: (2010)

Which one of the schedules below is the correct serialization of the above?
(a) T1 → T3 → T2
(b) T2 → T1 → T3
(c) T2 → T3 → T1
(d) T3 → T1 → T2
Ans:(a)
Sol: create precedence graph and apply Topological sort on it to obtain
T1 → T3 → T2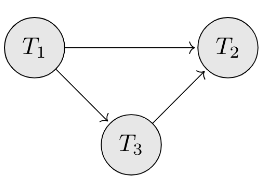
Q24: Which of the following concurrency control protocols ensure both conflict serializability and freedom from deadlock? (2010)
I. 2-phase locking
II. Time-stamp ordering
(a) I only
(b) II only
(c) Both I and II
(d) Neither I nor II
Ans: (b)
Sol: In basic two phase locking there is a chance for deadlock
Conservative 2pl is deadlock free
I go with B.
|
62 videos|66 docs|35 tests
|
FAQs on Previous Year Questions: Transaction - Database Management System (DBMS) - Computer Science Engineering (CSE)
| 1. What is a transaction in computer science? |  |
| 2. What is the importance of transactions in databases? |  |
| 3. What are the properties of a transaction in computer science? |  |
| 4. How does a database management system ensure the atomicity of a transaction? |  |
| 5. Why is isolation important in transactions? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
 T1 → T2 due to R1 (Y) being before W2 (Y)
T1 → T2 due to R1 (Y) being before W2 (Y) 
















