Q21: A balanced (positive sequence) three-phase AC voltage source is connected to a balanced, star connected load through a star-delta transformer as shown in the figure. The line-to-line voltage rating is 230 V on the star side, and 115 V on the delta side. If the magnetizing current is neglected and 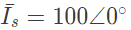 A, then what is the value of
A, then what is the value of 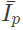 in Ampere? (SET-2 (2015)
in Ampere? (SET-2 (2015)
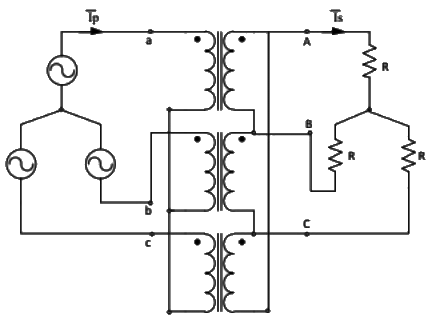 (a) 50 ∠ 30°
(a) 50 ∠ 30°
(b) 50 ∠−30 °
(c) 50√3 ∠ 30°
(d) 200∠30°
Ans: (a)
Q22: Two single-phase transformers T1 and T2 each rated at 500 kVA are operated in parallel. Percentage impedances of T1 and T2 are (1 + j6) and (0.8 + j4.8), respectively. To share a load of 1000 kVA at 0.8 lagging power factor, the contribution of T2 (in kVA) is ________. (SET-1 (2015))
(a) 224
(b) 258
(c) 426
(d) 556
Ans: (d)
Sol: 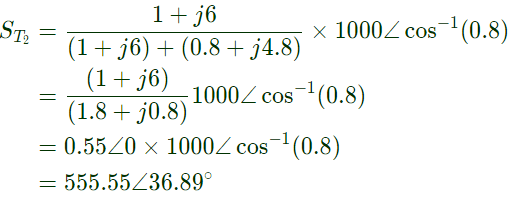
Q23: A 200/400 V, 50 Hz, two-winding transformer is rated at 20 kVA. Its windings are connected as an auto-transformer of rating 200/600 V. A resistive load of 12 Ω is connected to the high voltage (600 V) side of the auto-transformer. The value of equivalent load resistance (in Ohm) as seen from low voltage side is _____. (SET-1 (2015))
(a) 1.15
(b) 1.33
(c) 1.84
(d) 2.25
Ans: (b)
Sol: 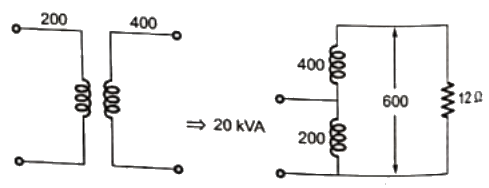
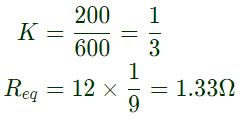
Q24: The primary mmf is least affected by the secondary terminal conditions in a (SET-1 (2015))
(a) power transformer.
(b) potential transformer.
(c) current transformer.
(d) distribution transformer.
Ans: (c)
Q25: The self inductance of the primary winding of a single phase, 50 Hz, transformer is 800 mH, and that of the secondary winding is 600 mH. The mutual inductance between these two windings is 480 mH. The secondary winding of this transformer is short circuited and the primary winding is connected to a 50 Hz, single phase, sinusoidal voltage source. The current flowing in both the windings is less than their respective rated currents. The resistance of both windings can be neglected. In this condition, what is the effective inductance (in mH) seen by the source? (SET-1 (2015))
(a) 416
(b) 440
(c) 200
(d) 920
Ans: (a)
Sol: Self inductance of primary coil is 500 mH.
Self inductance of secondary coil is 600 mH.
Mutual inductance is 480 mH.
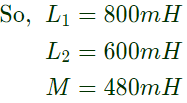
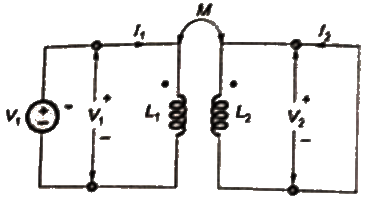 The voltage source V1 is sinusoidal with frequency 50 Hz.
The voltage source V1 is sinusoidal with frequency 50 Hz.
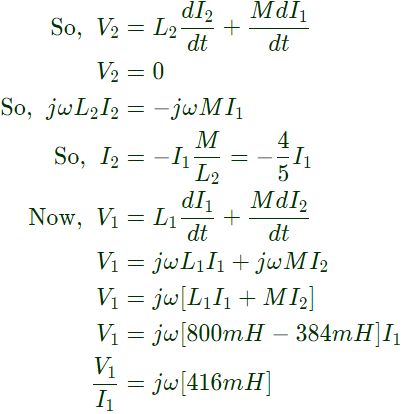 So, equivalent inductance is 416mH.
So, equivalent inductance is 416mH.
Q26: The parameters measured for a 220 V/110 V, 50 Hz, single phase transformer are :
Self inductance of primary winding = 45mH
Self inductance of secondary winding = 30 mH
Mutual inductance between primary and secondary windings = 20 mH
Using the above parameters, the leakage (Ll1, Ll2) and magnetizing (Lm) inductance as referred to primary side in the equivalent circuit respectively, are (SET-3 (2014))
(a) 5 mH, 20 mH and 40 mH
(b) 5 mH, 80 mH and 40 mH
(c) 25 mH, 10 mH and 20 mH
(d) 45 mH, 30 mH and 20 mH
Ans: (b)
Sol: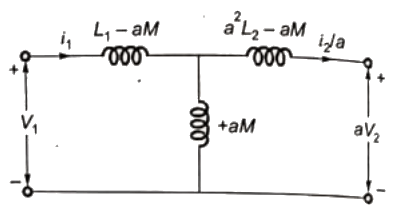
Q27: The load shown in the figure absorbs 4 kW at a power factor of 0.89 lagging
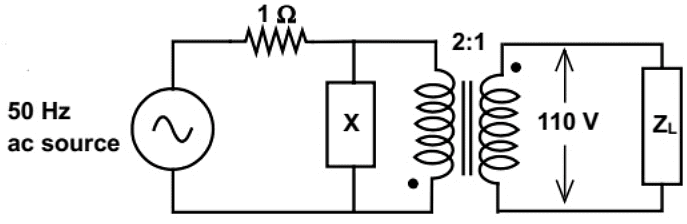 Assuming the transformer to be ideal, the value of the reactance X to improve the input power factor to unity is _________. (SET-3 (2014))
Assuming the transformer to be ideal, the value of the reactance X to improve the input power factor to unity is _________. (SET-3 (2014))
(a) 36.45
(b) 23.61
(c) 18.86
(d) 8.48
Ans: (b)
Sol: 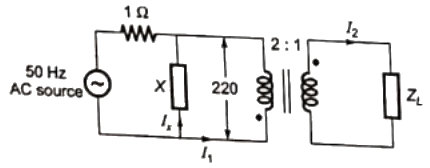
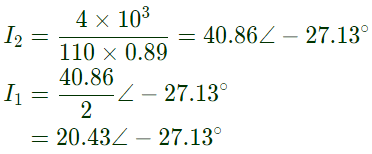
 For unity pf horizontal component of (I1) should be cancelled with (Ix).
For unity pf horizontal component of (I1) should be cancelled with (Ix).
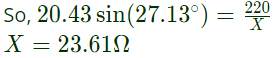
Q28: An open circuit test is performed on 50 Hz transformer, using variable frequency source and keeping V/f ratio constant, to separate its eddy current and hysteresis losses. The variation of core loss/frequency as function of frequency is shown in the figure
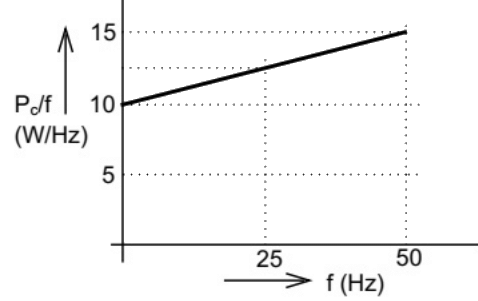 The hysteresis and eddy current losses of the transformer at 25 Hz respectively are (SET-3 (2014))
The hysteresis and eddy current losses of the transformer at 25 Hz respectively are (SET-3 (2014))
(a) 250 W and 2.5 W
(b) 250 W and 62.5 W
(c) 312.5 W and 62.5 W
(d) 312.5 W and 250 W
Ans: (b)
Sol: 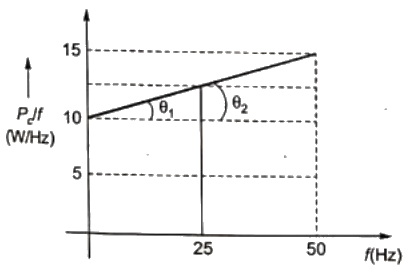 Let core loss at 25 Hz be P0 per Hz:
Let core loss at 25 Hz be P0 per Hz:
Then equating the two slopoes of figure, we have: 
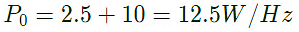 ∴ Core loss at 25Hz = 12.5 × 25 = 312.5watt
∴ Core loss at 25Hz = 12.5 × 25 = 312.5watt
Also, core loss at 50 Hz = 15 × 50 = 750watt
Let at (f1) 25 Hz, eddy current loss = Pe1 and hysteresis loss = Ph1 we know that, Pe ∝ f2
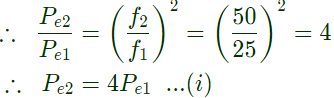
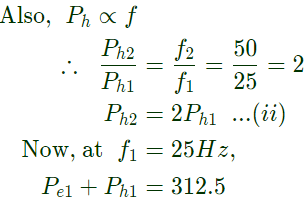
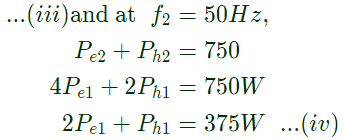 Solving equation (iii) and (iv), we get,
Solving equation (iii) and (iv), we get,
Pe1 = 62.5W and Ph1 = 250W
Thus, at 25 Hz, hysteresis loss = 250W and eddy current loss = 62.5W
Q29: A single phase, 50 kVA, 1000 V/100 V two winding transformer is connected as an autotransformer as shown in the figure.
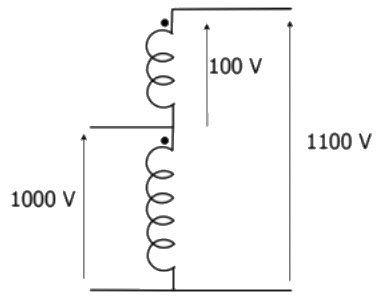 The kVA rating of the autotransformer is ________. (SET-2 (2014))
The kVA rating of the autotransformer is ________. (SET-2 (2014))
(a) 225
(b) 550
(c) 685
(d) 748
Ans: (b)
Sol: From the figure, autotransformation ratio,
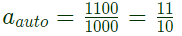 we know that,
we know that,
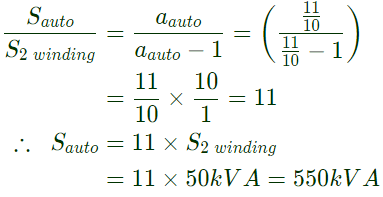
Q30: The core loss of a single phase, 230/115 V, 50 Hz power transformer is measured from 230 V side by feeding the primary (230 V side) from a variable voltage variable frequency source while keeping the secondary open circuited. The core loss is measured to be 1050 W for 230 V, 50 Hz input. The core loss is again measured to be 500 W for 138 V, 30 Hz input. The hysteresis and eddy current losses of the transformer for 230 V, 50 Hz input are respectively, (SET-1 (2014))
(a) 508 W and 542 W
(b) 468 W and 582 W
(c) 498 W and 552 W
(d) 488 W and 562 W
Ans: (a)
Sol: Given, at 230V, 50 Hz, core loss = 1050 W
and at 138 V, 30 Hz, core loss = 500 W
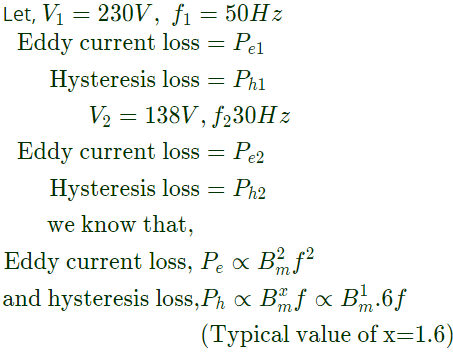 The transformer induced emf equation is:
The transformer induced emf equation is:
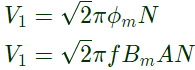 where, V/t = constant
where, V/t = constant
i.e. flux = constant ( to avoid over fluxing)
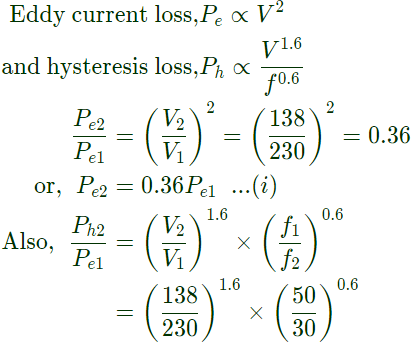
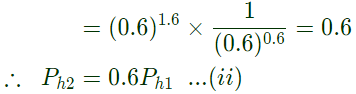 Given at 230V, 50Hz
Given at 230V, 50Hz
Core loss = Pe1 + Ph1 = 1050W...(iii)
At 138V, 30Hz,
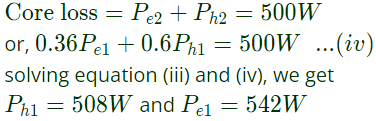 Therefore, hysteresis and eddy current losses at 230V, 50Hz are 508W and 542W respectively.
Therefore, hysteresis and eddy current losses at 230V, 50Hz are 508W and 542W respectively.
Q31: For a specified input voltage and frequency, if the equivalent radius of the core of a transformer is reduced by half, the factor by which the number of turns in the primary should change to maintain the same no load current is (SET-1 (2014))
(a) 1/4
(b) 1/2
(c) 2
(d) 4
Ans: (c)
Sol: Relucatance will be increased by two times. By considering flux density as constantflux should be reduced to 25% as area is reduced to 25%
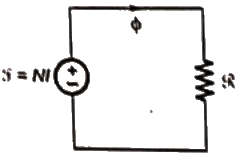
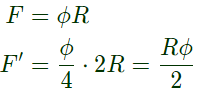 For given current, number of turns should be reduced by half.
For given current, number of turns should be reduced by half.
Q32: A single-phase transformer has no-load loss of 64W, as obtained from an open circuit test. When a short-circuit test is performed on it with 90% of the rated currents flowing in its both LV and HV windings, he measured loss is 81 W. The transformer has maximum efficiency when operated at (2013)
(a) 50.0% of the rated current
(b) 64.0% of the rated current
(c) 80.0% of the rated current
(d) 88.8% of the rated current
Ans: (c)
Sol: For 90% current,
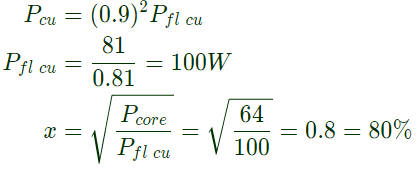
Q33: A single phase 10 kVA, 50 Hz transformer with 1 kV primary winding draws 0.5 A and 55W, at rated voltage and frequency, on no load. A second transformer has a core with all its linear dimensions√2 times the corresponding dimensions of the first transformer. The core material and lamination thickness are the same in both transformer. The primary winding of both the transformers have the save number of turns. If a rate voltage of 2 kV at 50 Hz is applied to the primary of the second transformer, then the no load current and power, respectively, are (2012)
(a) 0.7 A, 77.8 A
(b) 0.7 A, 155.6W
(c) 1A, 110W
(d) 1A, 220W
Ans: (b)
Sol: We know, E = √2π N f ϕm,
As N and f are constant,
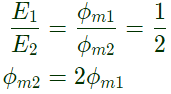 and also,
and also,
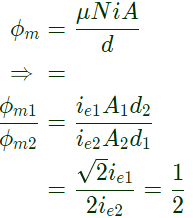
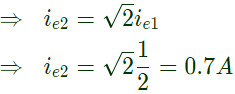
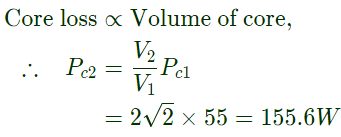
Q34: A single phase air core transformer, fed from a rated sinusoidal supply, is operating at no load. The steady state magnetizing current drawn by the transformer from the supply will have the waveform (2011)
(a) 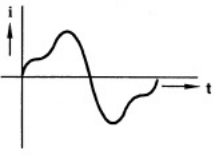 (b)
(b) 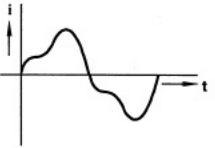 (c)
(c) 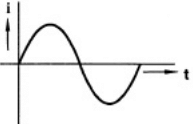 (d)
(d) 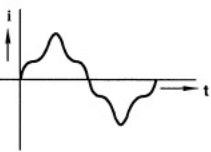 Ans: (c)
Ans: (c)
Sol: The transformer is fed from sinusoidal supply, so flux (ϕ) set up in the transformer is also sinusoidal. As the transformer is air cored, there will be no saturation and hysteresis effect in transformer. So B-H curve is linear, due to which magnetizing current is also sinusoidal.
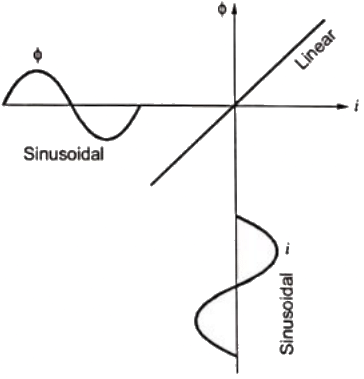
Q35: A balanced star-connected and purely resistive load is connected at the secondary of a star-delta transformer as shown in figure. The line-to line voltage rating of the transformer is 110 V/200 V. Neglecting the non-idealities of the transformer, the impedance Z of the equivalent star-connected load, referred to the primary side of the transformer, is (2010)
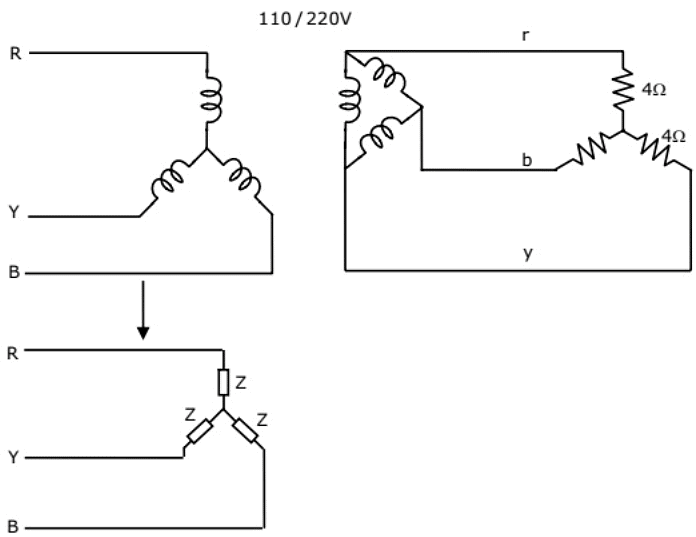 (a) (3 + j0)Ω
(a) (3 + j0)Ω
(b) (0.866 + j0.5)Ω
(c) (0.866 − j0.5)Ω
(d) (1 + j0)Ω
Ans: (d)
Sol: 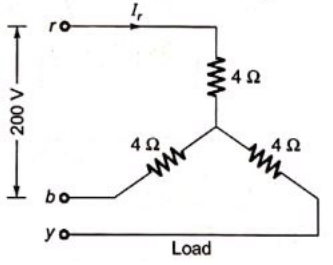 Let VA rating of the transformer S.
Let VA rating of the transformer S.
Rated voltage (line to line) on secondary side = 200V
Rated current 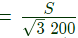
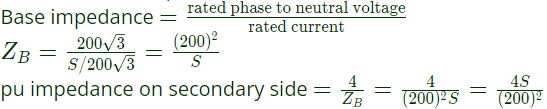 pu impedance in primary side and secondary side are equal.
pu impedance in primary side and secondary side are equal.
Therefore pu impedance on primary side 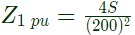
Rated phase to neutral voltage on primary side 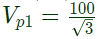
Rated primary current (phase) 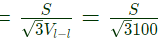
Base impedance 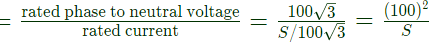
Load impedance reffered to primary side Z1= base impedance (primary side) × pu impedance

Q36: A Single-phase transformer has a turns ratio 1 : 2, and is connected to a purely resistive load as shown in the figure. The magnetizing current drawn is 1 A, and the secondary current is 1 A. If core losses and leakage reactance's are neglected, the primary current is (2010)
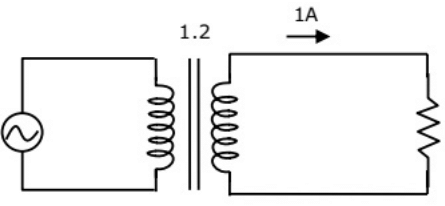 (a) 1.41A
(a) 1.41A
(b) 2A
(c) 2.24 A
(d) 3A
Ans: (c)
Sol: Secondary current
I2 = 1 ∠ 0°
A Secondary current referred to primary side
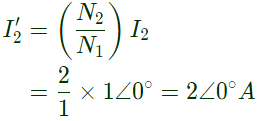 As the core losses are neglected, magnetizing current (Im) will be in phase with flux (ϕ). Therefore Im lags the induced emf by 90°Im = 1∠−90°A
As the core losses are neglected, magnetizing current (Im) will be in phase with flux (ϕ). Therefore Im lags the induced emf by 90°Im = 1∠−90°A
Primary current,
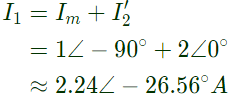
Q37: The figure below shows coils-1 and 2, with dot markings as shown, having 4000 and 6000 turns respectively. Both the coils have a rated current of 25 A. Coil-1 is excited with single phase, 400 V, 50 Hz supply.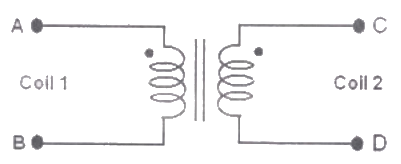 The current in each coil is (2009)
The current in each coil is (2009)
(a) Coil-1 is 25 A and Coil-2 is 10 A
(b) Coil-1 is 10 A and Coil-2 is 25 A
(c) Coil-1 is 10 A and Coil-2 is 15 A
(d) Coil-1 is 15 A and Coil-2 is 10 A
Ans: (d)
Sol: 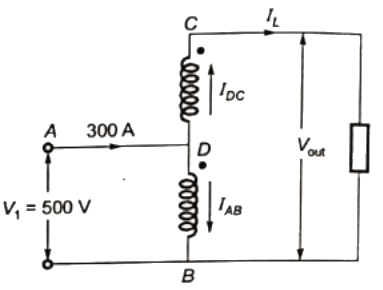 Load connecetd= S = 10k VA
Load connecetd= S = 10k VA
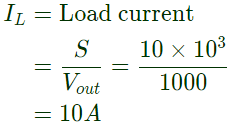 Current through coil 2
Current through coil 2
IDC = IL = 10A
Input current of autotransformer
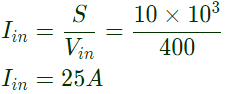 Using KCL,
Using KCL,
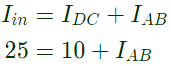 Current through coil 1 = IAB = 15A
Current through coil 1 = IAB = 15A
Q38: The figure below shows coils-1 and 2, with dot markings as shown, having 4000 and 6000 turns respectively. Both the coils have a rated current of 25 A. Coil-1 is excited with single phase, 400 V, 50 Hz supply.
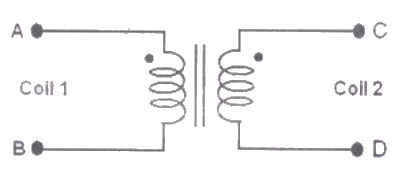 The coils are to be connected to obtain a single-phase, (400/1000) V, auto-transformer to drive a load of 10 kVA. Which of the options given should be exercised to realize the required auto-transformer ? (2009)
The coils are to be connected to obtain a single-phase, (400/1000) V, auto-transformer to drive a load of 10 kVA. Which of the options given should be exercised to realize the required auto-transformer ? (2009)
(a) Connect A and D; Common B
(b) Connect B and D; Common C
(c) Connect A and C; Common B
(d) Connect A and C; Common D
Ans: (a)
Sol: 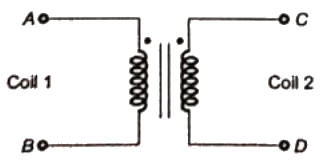
 The two coils are connected to obatin step up auto transformer (400/1000) V.
The two coils are connected to obatin step up auto transformer (400/1000) V.
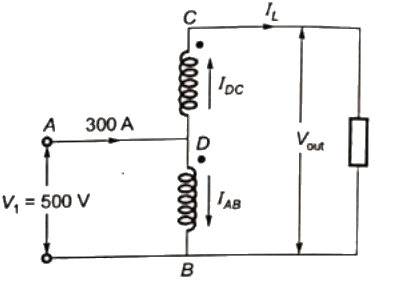
 = 400 + 600
= 400 + 600
= 1000 V
Q39: The circuit diagram shows a two-winding, lossless transformer with no leakage flux, excited from a current source, i(t), whose waveform is also shown. The transformer has a magnetizing inductance of 400/π mH.
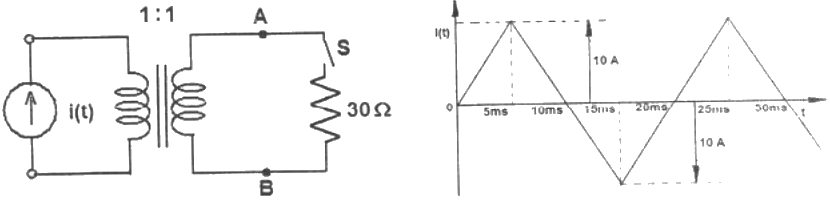 If the wave form of i(t) is changed to i(t) = 10 sin(100 πt) A, the peak voltage across A and B with S closed is (2009)
If the wave form of i(t) is changed to i(t) = 10 sin(100 πt) A, the peak voltage across A and B with S closed is (2009)
(a) 400 V
(b) 240 V
(c) 320 V
(d) 160 V
Ans: (b)
Sol: When s is closed the equivalnet circuit,
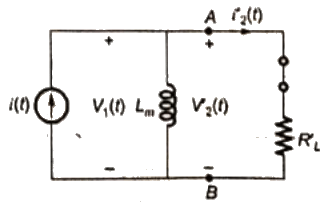 Here,
Here,
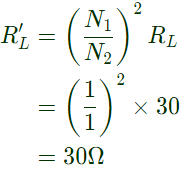 Load current referred to primary side,
Load current referred to primary side,
 Load voltage referred to primary side,
Load voltage referred to primary side,
 so, secondary voltage across A and B
so, secondary voltage across A and B
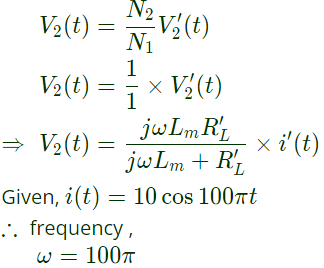
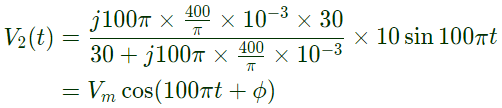 Peak value of secondary voltage,
Peak value of secondary voltage,
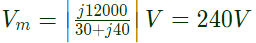
Q40: The circuit diagram shows a two-winding, lossless transformer with no leakage flux, excited from a current source, i(t), whose waveform is also shown. The transformer has a magnetizing inductance of (400/π) mH.
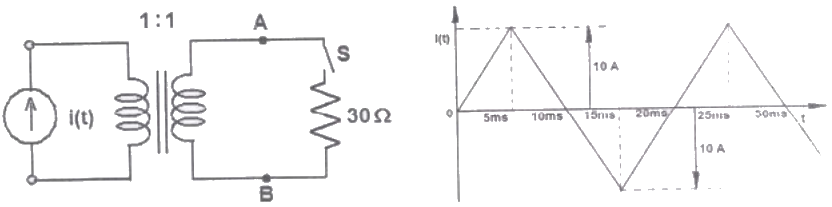 The peak voltage across A and B, with S open is (2009)
The peak voltage across A and B, with S open is (2009)
(a) (400/π) V
(b) 800 V
(c) (4000/π) V
(d) (800/π) V
Ans: (d)
Sol: 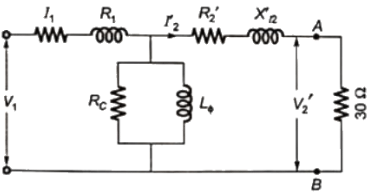 No leakage flux ⇒ Xl1 and X'l2 are neglected.
No leakage flux ⇒ Xl1 and X'l2 are neglected.
Transformer is lossless ⇒ R1, R'2 and Rc are neglected.
Lϕ = magnetizing inductances = (400/π) mH
Therefore, the above equivalent circuit can be redrawn with S open.

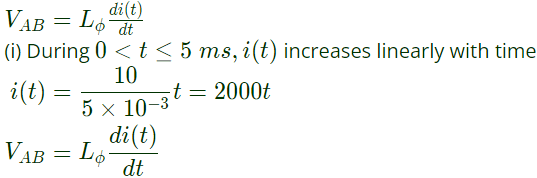
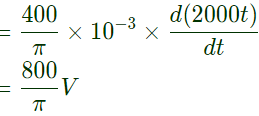
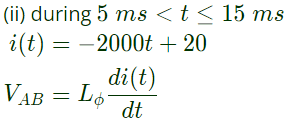
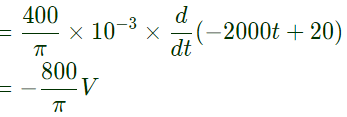 (iii) During 150ms < t ≤ 25ms
(iii) During 150ms < t ≤ 25ms
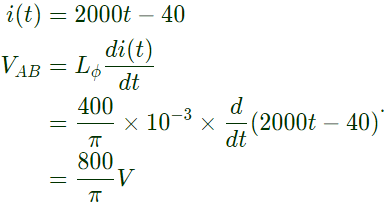
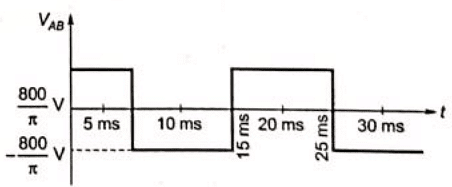 Therefore, peak voltage across A nad B
Therefore, peak voltage across A nad B 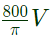 .
.
 A, then what is the value of
A, then what is the value of 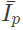 in Ampere? (SET-2 (2015)
in Ampere? (SET-2 (2015) (a) 50 ∠ 30°
(a) 50 ∠ 30°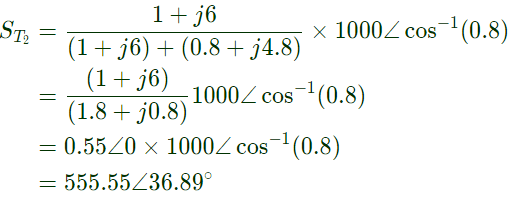

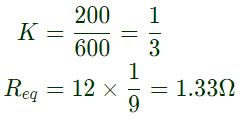
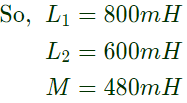
 The voltage source V1 is sinusoidal with frequency 50 Hz.
The voltage source V1 is sinusoidal with frequency 50 Hz.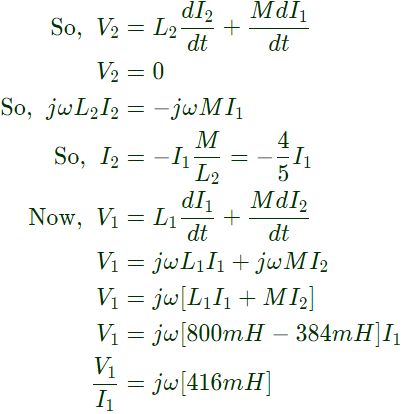 So, equivalent inductance is 416mH.
So, equivalent inductance is 416mH. 
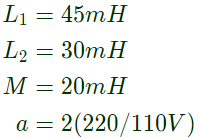
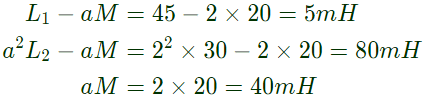
 Assuming the transformer to be ideal, the value of the reactance X to improve the input power factor to unity is _________. (SET-3 (2014))
Assuming the transformer to be ideal, the value of the reactance X to improve the input power factor to unity is _________. (SET-3 (2014))
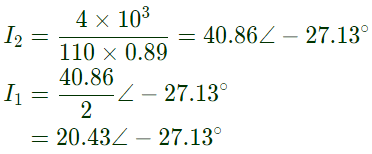
 For unity pf horizontal component of (I1) should be cancelled with (Ix).
For unity pf horizontal component of (I1) should be cancelled with (Ix).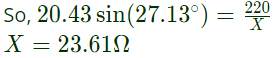
 The hysteresis and eddy current losses of the transformer at 25 Hz respectively are (SET-3 (2014))
The hysteresis and eddy current losses of the transformer at 25 Hz respectively are (SET-3 (2014)) Let core loss at 25 Hz be P0 per Hz:
Let core loss at 25 Hz be P0 per Hz:
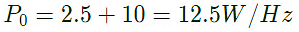 ∴ Core loss at 25Hz = 12.5 × 25 = 312.5watt
∴ Core loss at 25Hz = 12.5 × 25 = 312.5watt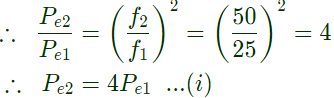
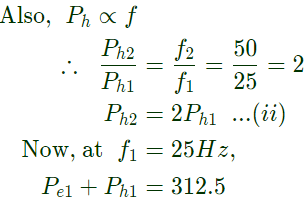
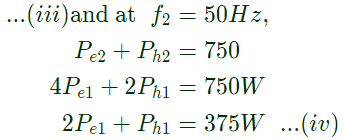 Solving equation (iii) and (iv), we get,
Solving equation (iii) and (iv), we get, The kVA rating of the autotransformer is ________. (SET-2 (2014))
The kVA rating of the autotransformer is ________. (SET-2 (2014))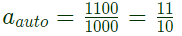 we know that,
we know that,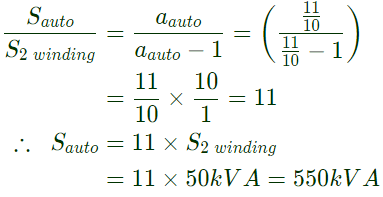
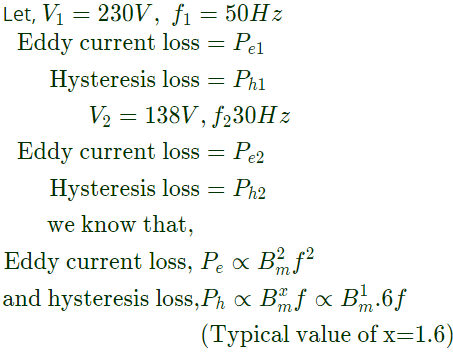 The transformer induced emf equation is:
The transformer induced emf equation is: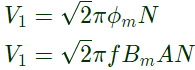 where, V/t = constant
where, V/t = constant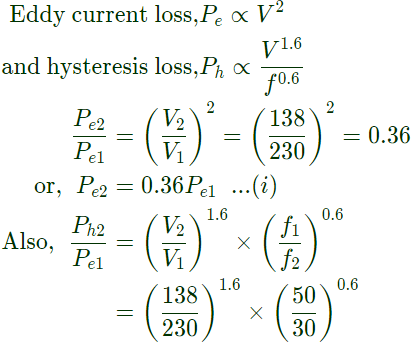
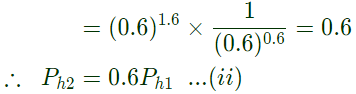 Given at 230V, 50Hz
Given at 230V, 50Hz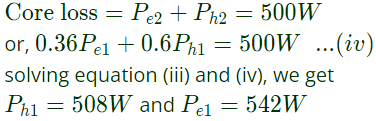 Therefore, hysteresis and eddy current losses at 230V, 50Hz are 508W and 542W respectively.
Therefore, hysteresis and eddy current losses at 230V, 50Hz are 508W and 542W respectively.
 For given current, number of turns should be reduced by half.
For given current, number of turns should be reduced by half.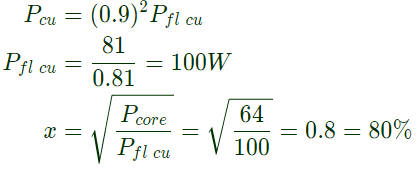
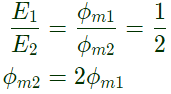 and also,
and also,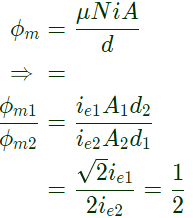
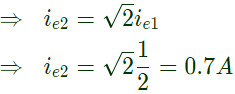
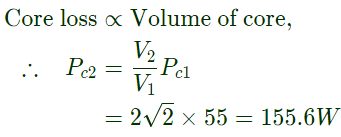
 (b)
(b)  (c)
(c)  (d)
(d)  Ans: (c)
Ans: (c)
 (a) (3 + j0)Ω
(a) (3 + j0)Ω Let VA rating of the transformer S.
Let VA rating of the transformer S.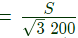
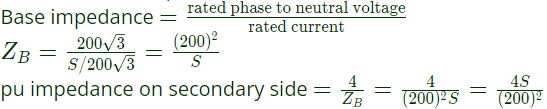 pu impedance in primary side and secondary side are equal.
pu impedance in primary side and secondary side are equal.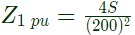
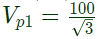
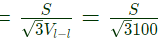
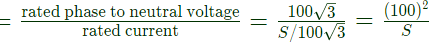

 (a) 1.41A
(a) 1.41A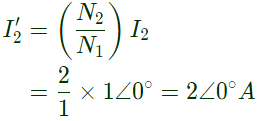 As the core losses are neglected, magnetizing current (Im) will be in phase with flux (ϕ). Therefore Im lags the induced emf by 90°Im = 1∠−90°A
As the core losses are neglected, magnetizing current (Im) will be in phase with flux (ϕ). Therefore Im lags the induced emf by 90°Im = 1∠−90°A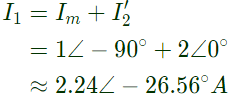
 The current in each coil is (2009)
The current in each coil is (2009) Load connecetd= S = 10k VA
Load connecetd= S = 10k VA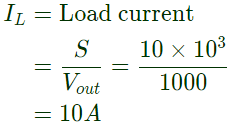 Current through coil 2
Current through coil 2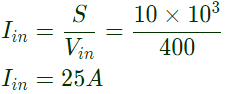 Using KCL,
Using KCL,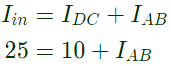 Current through coil 1 = IAB = 15A
Current through coil 1 = IAB = 15A The coils are to be connected to obtain a single-phase, (400/1000) V, auto-transformer to drive a load of 10 kVA. Which of the options given should be exercised to realize the required auto-transformer ? (2009)
The coils are to be connected to obtain a single-phase, (400/1000) V, auto-transformer to drive a load of 10 kVA. Which of the options given should be exercised to realize the required auto-transformer ? (2009)
 The two coils are connected to obatin step up auto transformer (400/1000) V.
The two coils are connected to obatin step up auto transformer (400/1000) V.
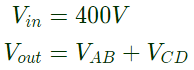 = 400 + 600
= 400 + 600  If the wave form of i(t) is changed to i(t) = 10 sin(100 πt) A, the peak voltage across A and B with S closed is (2009)
If the wave form of i(t) is changed to i(t) = 10 sin(100 πt) A, the peak voltage across A and B with S closed is (2009) Here,
Here,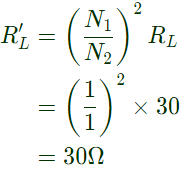 Load current referred to primary side,
Load current referred to primary side, Load voltage referred to primary side,
Load voltage referred to primary side, so, secondary voltage across A and B
so, secondary voltage across A and B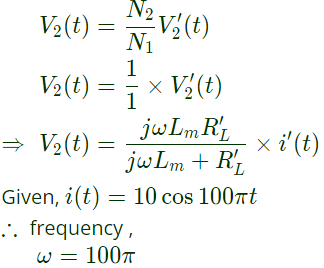
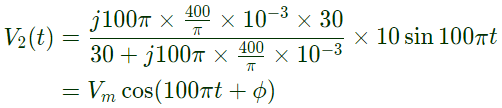 Peak value of secondary voltage,
Peak value of secondary voltage,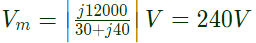
 The peak voltage across A and B, with S open is (2009)
The peak voltage across A and B, with S open is (2009) No leakage flux ⇒ Xl1 and X'l2 are neglected.
No leakage flux ⇒ Xl1 and X'l2 are neglected.
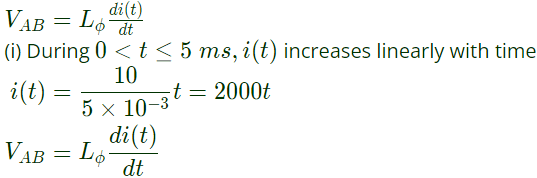
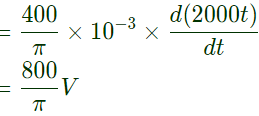
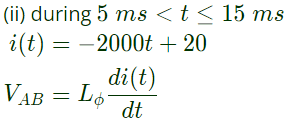
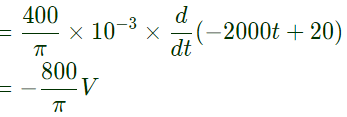 (iii) During 150ms < t ≤ 25ms
(iii) During 150ms < t ≤ 25ms 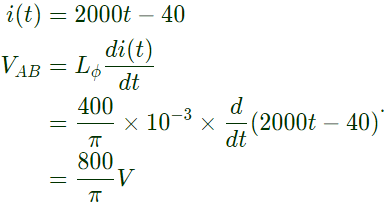
 Therefore, peak voltage across A nad B
Therefore, peak voltage across A nad B 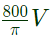 .
.




















