Class 9 Science Chapter 10 Previous Year Questions - Work and Energy
Short Answer Type Questions
Q.1. A truck of mass 1800 kg is moving with a speed of 54 km/h. When the brakes are applied, it stops with uniform negative acceleration at a distance of 200 m. Calculate the force applied by the brakes of the truck and the work done before stopping. [2025]
Ans: Given:
- Mass, m = 1800 kg
- Initial velocity, u = 54 km/h = 15 m/s
- Final velocity, v = 0 m/s
- Distance, s = 200 m
Calculations:
Retardation, a 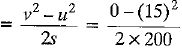
= 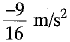
Force, F = ma = 1800 x 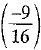
= -1012.5 N
The negative sign indicates force acts in the opposite direction to motion.
Work done = Fs = 1012.5 x 200
= 202500 J
Q.2. Define power. [ 2025]
Ans: Power is defined as the rate at which work is done or energy is transferred. Power measures how quickly work is performed.
- Unit of Power: The standard unit is the watt (W), which is equivalent to one joule per second (1 W = 1 J/s).
- Example: If an agent does work (W) in time (t), power (P) can be calculated using the formula: P = W/t.
- Energy Transfer: Power also indicates the speed of energy consumption, with larger rates expressed in kilowatts (1 kW = 1000 W).
Q.3. State the law of conservation of energy. [2024]
Ans: The Law of Conservation of Energy states that:
- Energy cannot be created or destroyed.
- It can only be transformed from one form to another.
- The total energy in a system remains constant before and after any transformation.
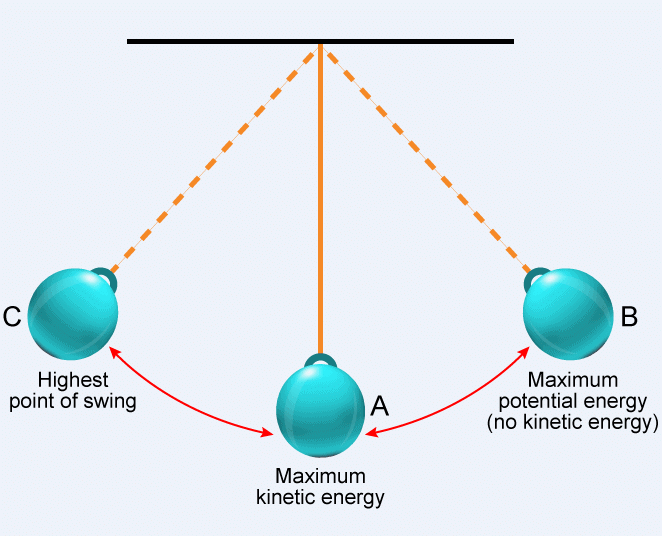 Illustration of Law of Conservation of Energy
Illustration of Law of Conservation of Energy
Q.4. State the type of transformation of energy during the ‘burning of a cracker’. [2023]
Ans: During the burning of a cracker, chemical energy is transformed into:
- Light energy
- Sound energy
This process illustrates how energy changes form during combustion.
Q.5. Why is the energy of an object increased when raised through a height? [2022]
Ans: When an object is raised to a height, it gains energy because:
- Work is done against its weight, which is the force of gravity.
- This work is stored as potential energy.
- Thus, the energy of the object increases as it is lifted.
Q.6. (a) Define kinetic energy.
(b) The masses of scooters and bikes are in the ratio of 2 :3, but both are moving with the same speed of 108 km/h. Compute the ratio of their kinetic energy. [2022]
Ans: (a) The energy possessed by a body by virtue of its motion is called kinetic energy.
(b) Kinetic energy ∝ Mass of body
Let mass of scooter = ms - 2m
and mass of bike = mb = 3m
∴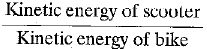
Q.7. A labourer whose own mass is 50 kg carries a load of an additional 60 kg on his head to the top of a building 15 m high. Find the total work done by him. Also, find the work done by him if he carries an additional block of mass 10 kg to the same height. (Take g = 10 m/s2) [2021]
Ans:
To calculate the total work done by the labourer, we consider:
- Mass of labourer: 50 kg
- Mass of load: 60 kg
- Height of building: 15 m
∴ Total force applied by labourer F = (m1 + m2)g
Work done W = Fs = (m1 + m2)gh = (50 + 60) x 10 x 15 = 16500 J
When the labourer carries an additional load of mass m3 = 10 kg, the total force
F' = (m1 + m2 + m3)g
Total work done W' - F's = (m1 + m2 + m3)gh
= (50 + 60 + 10) x 10 x 15 = 18000 J
Q.8. What is the work to be done to increase the velocity of a car from 36 km h-1 to 72 km h-1 if the mass of car is 1500 kg? [2021]
Ans:
To calculate the work needed to increase the velocity of a car, we can use the change in its kinetic energy.
- Mass of the car: 1500 kg
- Initial velocity (u): = 36 km h-1 =
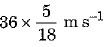
= 10 m s-1 - Final velocity (v): 72 km h-1
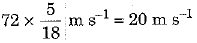
The work done (W) is equal to the change in kinetic energy:
⇒ 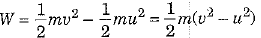
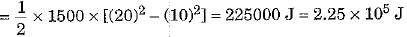
Q.9. A body of mass 3 kg is thrown vertically upwards with an initial velocity of 20 m/s. What will be its potential energy at the end of 2 s? (Take g = 10 m/s-2) [2021]
Ans: To calculate the potential energy of a body thrown vertically upwards, we need to determine its height after 2 seconds.
- Mass of the body: 3 kg
- Initial velocity: 20 m/s
- Acceleration due to gravity: 10 m/s2
- Time: 2 s
After a time t = 2 s, the body is at a height h, where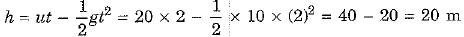
∴ Potential energy of body at t = 2 s, Ep = mgh = 3 x 10 x 20 = 600 J
Q.10. A car is moving on a levelled road and gets its velocity doubled. In this process:
(а) How would the potential energy of the car change?
(b) How would the kinetic energy of the car change?
(c) How will its momentum change?
Give reasons for your answer. [2021]
Ans: (a) The potential energy remains unchanged as the car is moving on a levelled road such that its height 'h' above the ground does not change, and potential energy Ep = mgh remains unchanged.
(b) When the velocity of the car is doubled v'/ = 2v), then its kinetic energy Ek increases to 4 times of its initial kinetic energy Ek as shown below :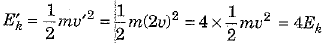
(c) The momentum 'p' of the car is given as : p = mv. When the velocity of the car is doubled, its momentum is also doubled to p' = 2p
p' = mv' - m(2v) = 2mv - 2p
Q.11. (a) Water is falling on the blades of a turbine at the rate of 6 x 103 kg per minute. The height of the fall is 10 m. Calculate the power given to the turbine.
(Take g = 10 m/s2)
(b) A driver speeds up his vehicle when he moves up a hill. Give a reason. [2020]
Ans: (a) The mass of water falling on the turbine blades is 6 x 103 kg per minute. To find the power given to the turbine, we first convert the time to seconds:
- Time, t = 1 minute = 60 s
- Height of the fall, h = 10 m
- Acceleration due to gravity, g = 10 m/s2
∴ Energy supplied to the turbine = Loss in potential energy of water = mgh
∴ 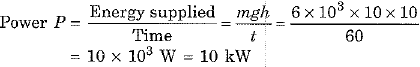
(b) When a driver moves his vehicle up a hill, the force of gravity opposes his motion, and he needs greater power. For this purpose, the driver speeds up his vehicle.
Q.12. A lamp consumes 500 J of electrical energy in 20 seconds. What is the power of the lamp? Also, find the electrical energy consumed in units if the lamp operates for 2 hours daily for 15 days. [2020]
Ans: The power of the lamp can be calculated using the formula:
- Energy consumed (E) = 500 J
- Time (t) = 20 s
- Power (P) = E / t = 500 J / 20 s = 25 W
Further electrical energy consumed by the lamp in operation for t = 2 hours daily for n = 15 days is
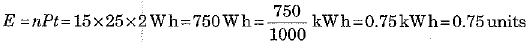
Q.13. Define one kilowatt hour (1 kW h). [2020]
Ans: One kilowatt hour (1 kWh) is a measure of energy consumption. It indicates the amount of energy used when:
- Energy is consumed at a rate of 1 kilowatt (1 kW).
- This consumption occurs over a period of 1 hour.
In simpler terms, if you use a device that consumes 1000 watts of power for one hour, it will use 1 kWh of energy.
Q.14. State the value of commercial units of energy in joules.
Or
State the relation between kWh and joules. [2020]
Ans: 1 kW h = 3.6 x 106 J.
Q.15. A body of mass 100 g is lifted to a height of 10 m. Find (i) the amount of work done, (ii) the potential energy of the body at that height. (Take g = 10 m s-2) [2019]
Ans: (i) To solve the problem, we start with the given values:
- Mass of the body (m): 100 g = 0.1 kg
- Height (h): 10 m
- Acceleration due to gravity (g): 10 m/s2
Now, we can calculate:
- Work done (W): This is the energy used to lift the body against gravity.
- Using the formula: W = mgh
- Substituting the values: W = 0.1 kg × 10 m/s2 × 10 m = 10 J
Thus, the work done is 10 J.
(ii) Potential energy (Ep): This is the energy stored in the body due to its height.
- Using the same formula: Ep = mgh
- Substituting the values: Ep = 0.1 kg × 10 m/s2 × 10 m = 10 J
Therefore, the potential energy at that height is also 10 J.
Q.16. Define power. State the commercial unit and SI unit of electrical energy. An electric heater of 400 W works for 2 hours. Find the electrical energy units consumed in a day. [2019]
Ans: Power is defined as the rate at which work is done or energy is transferred. It indicates how quickly energy is used or work is performed.
- Commercial unit of energy: kilowatt-hour (kWh)
- SI unit of energy: joule (J)
For an electric heater with a power of 400 W (or 0.4 kW) operating for 2 hours, the energy consumed in a day can be calculated as follows:
- Energy consumed = Power × Time
- Energy consumed = 0.4 kW × 2 h = 0.8 kWh
Q.17. State two factors on which the magnitude of gravitational potential energy depends. [2019]
Ans: The magnitude of gravitational potential energy of an object depends on:
- Mass of the object
- Height above the ground level
Q.18. Distinguish between positive work and negative work. When you lift an object up, two forces act on it. Identify these forces. Which one of the two does:
(a) Positive work
(b) Negative work
Justify your answer. [2019]
Ans: Positive work occurs when the displacement of an object is in the same direction as the applied force. In contrast, negative work happens when the displacement is in the opposite direction to the force. When lifting an object, two forces act on it:
- Force due to gravity (F = mg): This force acts downwards.
- Applied force (F): This force acts upwards.
In this scenario:
(a) The applied force does positive work because it moves the object upwards.
(b) The force of gravity does negative work as it acts in the opposite direction to the displacement.
Thus, the direction of the forces relative to the displacement determines whether the work done is positive or negative.
Q.19. An object of mass 10 kg is dropped from a height of 100 cm. Find its :
(a) kinetic energy
(b ) velocity, just as it reaches the ground, (g = 10 m/s2) [2018]
Ans: Here mass of object m = 10 kg, height from which dropped h = 100 cm = 1 m and g = 10 m s-2.
(a) K.E. of obiect on reaching ground Ek = 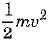 = Gravitational potential energy before falling = msh = 10 x 10 x 1 = 100J
= Gravitational potential energy before falling = msh = 10 x 10 x 1 = 100J
(b) ∵ 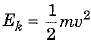 , hence velocity v =
, hence velocity v = 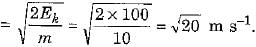
Q.20. In a factory 10 bulbs of 50 W, each and 5 fans of 70 W each operate for 12 hours daily. Calculate the units of electricity consumed. Also, find the expenditure if 1 unit costs Rs 2. [2018]
Ans: Here energy consumed in a factory for running 10 bulbs of 50 W each when used for 12 hours
E1 - 10 x 50 x 12 = 6000 W h = 6.0 kW h
and energy consumed in the factory 5 fans of 70 W each for 12 hours
E2 = 5 x 70 x 12 = 4200 W h = 4.2 kW h
∴ Total electricity consumed E = E1 + E2 = 6.0 + 4.2 = 10.2 kW h = 10.2 units
∴ Total expenditure @ Rs. 2.00 per unit = 2 x 10.2 = Rs. 20.4
Q.21. (a) A moving body of mass 20 kg has 40 joules of kinetic energy. Calculate its speed.
(b) A person carrying a load of 20 kg climbs 4 m in 10 seconds. Calculate the work done and his power, (g = 10 m/s2) [2017]
Ans: Given: Mass, m = 20 kg; Kinetic energy, Ek = 40 J;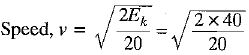
= 2 m/s
(b) Given: Mass, m = 20 kg; Height, h = 4 m; Time, t = 10 s; g = 10 ms-2
Work done, W = mgh
= 20 x 10 x 4 = 800 J
and 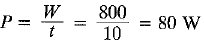
Long Answer Type Questions
Q.1. (a) Define work. Give the SI unit of work. Write an expression for the positive work done.
(b) Calculate the work done in pushing acai through a distance of 50 m against the force of friction equal to 250 N. Also state the type of work done.
(c) Sarita lives on 3rd floor of the building at a height of 15 m. She carries her school bag weighing 5.2 kg from the ground floor to her house. Find the amount of work done by her and identify the force against which she has done work (g = 10 ms-2) [2025]
Ans: (a) Work is said to be done if an applied force displaces a body in its own direction.
Its SI unit is joule (J).
Positive work done, W = F.s,
where F = force; 5 = displacement is the direction of force.
(b) Given: Distance, s = 50 m; Force, f = 250
N (opposite to the direction of friction)
Work, W = F .s = 250N x 50m = 12500 J Work done by applied force is positive and by friction is negative.
(c) Given: Mass, m = 5.2 kg; g = 10 m s-2; height h = 15 m
Work done = mgh = 5.2 x 10 x 15 = 780 J
Work is done against the force of gravity acting on the bag.
Q.2. (a) Define kinetic energy. Obtain an expression for the kinetic energy of an object.
(b) A ball of mass 400 g rolls on the ground with a uniform speed of 25 ms-1. Find the kinetic energy possessed by it. [2024]
Ans: (a) Kinetic energy of an object is the energy possessed by it by virtue of its state of motion. Every moving object possesses kinetic energy.
Consider an object of mass m in a state of motion with an initial velocity u. Let a constant force F act on it and displace the body through a distance s in the direction of the force applied.
∴ Work was done on the object W = Fs
Due to the work done on the body, let the velocity of the object change from u to v and a be the acceleration produced.
Then, according to the equation of motion
v2 - u2 = 2as
⇒ 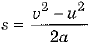
Again, according to the second law of motion,
we have F = ma
∴ Work was done on the object W = Fs = (ma)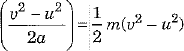
If the object started from rest, then u = 0 and hence W = 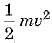
The work done on the object is equal to the kinetic energy imparted to the object. Thus, the kinetic energy possessed by an object of mass m moving with a uniform velocity v is given by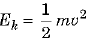
(b) Here mass of ball m = 400 g - 0.4 kg and speed of ball v = 25 m s-1.
∴ Kinetic energy of the ball Ek = 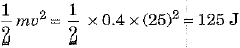
Q.3. Calculate the electricity bill amount for a month of 30 days, if the following devices are used as specified :
(a) 3 bulbs of 40 W for 6 hours.
(b) 4 tube light of 50 W for 6 hours.
(c) A refrigerator of 320 W for 24 hours.
Given the rate of electricity is Rs. 2.50 per unit. [2023]
Ans: As per the data given energy consumed per day in kWh units is :
(a) for using 3 bulbs of 40 W each for 6 hours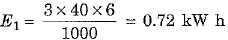
(b) for using 4 tube lights of 50 W each for 6 hours
(c) for running a refrigerator of 320 W for 24 hours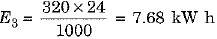
∴ Total energy consumed per day E - E1 + E2 + E3 = 0.72 + 1.2 + 7.68 = 9.60 kW h
∴ Total energy consumed during a month of 30 days = 30 x 9.60 kW h = 288 units
∴ Electricity bill @ Rs. 2.50 per unit - Rs. 2.50 x 288 = Rs. 720
Q.4. (a) Define the work done by a constant force. Write its SI unit and define this unit.
(b) A 3000 kg truck moving at a speed of 72 km/h stops after covering some distance. The force applied by brakes is 24000 N. Compute the distance covered and work done by this force. [2023]
Ans: (a) The work done by a constant force is defined as the product of the force applied and the distance moved in the direction of that force. It can be expressed as:
- Work (W) = Force (F) × Displacement (s)
The SI unit of work is the joule (J). One joule is defined as the work done when a force of 1 newton displaces an object by 1 metre in the direction of the force.
(b) Here mass of truck m = 3000 kg, initial speed u = 72 km/h 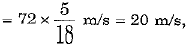
final speed u = 0 and force applied by brakes F - 24000 N
As the force of brakes opposes motion, we take it negatively, that is F = 24000 N
∴ Acceleration of the truck a = 
Using the relation v2 - u2 = 2as, we have
Distance covered 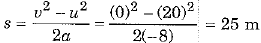
and work done by the force W = Fs = (- 24000) x 25 = - 600000 J = -6x 105 J
|
84 videos|478 docs|60 tests
|
FAQs on Class 9 Science Chapter 10 Previous Year Questions - Work and Energy
| 1. What is the work-energy theorem? |  |
| 2. How can we calculate work done on an object? |  |
| 3. What is the difference between kinetic energy and potential energy? |  |
| 4. How is energy conserved during work done on an object? |  |
| 5. What are some real-life examples of work and energy concepts? |  |






















