JEE Main Previous Year Questions (2016- 2024): Indefinite Integrals | Mathematics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Q.1. The integral  is equal to (where C is a constant of integration) (2020)
is equal to (where C is a constant of integration) (2020)
(1) 
(2) 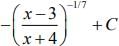
(3) 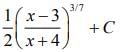
(4) 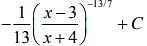
Ans. (1)
Let,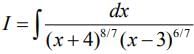
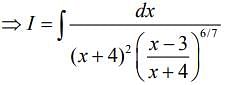
Let 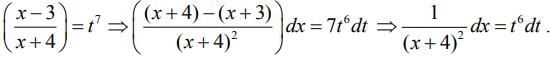
So, 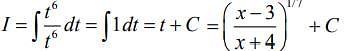
Q.2. If 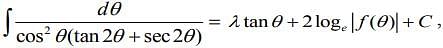 where C is a constant of integration, then the ordered pair (λ, f(θ)) is equal to (2020)
where C is a constant of integration, then the ordered pair (λ, f(θ)) is equal to (2020)
(1) (1,1 tan θ)
(2) ( 1,1 -tan θ)
(3) (-1,1 + tan θ)
(4) (1,1 + tan θ)
Ans. (3)
We have
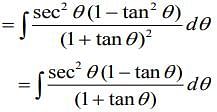
Let tan θ = t ⇒sec2 θdθ = dt.
Therefore,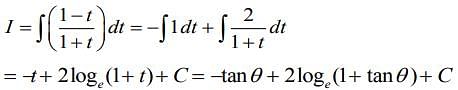
Hence, 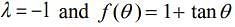
Q.3. For x2 ≠ nπ + 1, n∈N (the set of natural numbers), the integral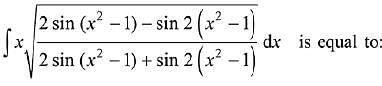 (2019)
(2019)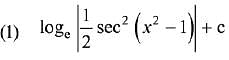
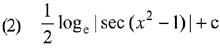

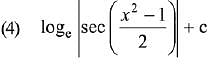
(where c is a constant of integration)
Ans. (3, 4)
Solution. Consider the given integral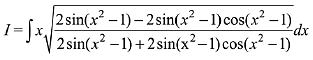
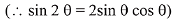
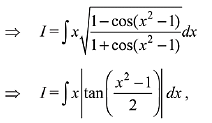
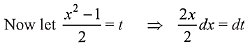
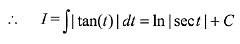
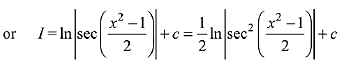
Q.4.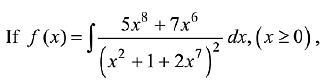 and f(0) = 0, then the value of f(1) is: (2019)
and f(0) = 0, then the value of f(1) is: (2019)
(3) 1/2
(4) 1/4
Ans. (4)
Solution.
f(x) =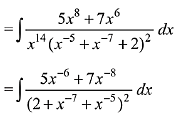
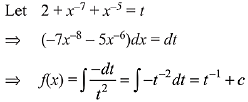
Q.5. Let n ≥ 2 be a natural number and 0 < θ < π/2. Then 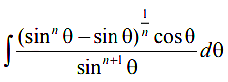 is equal to (where C is a constant of integration (2019)
is equal to (where C is a constant of integration (2019)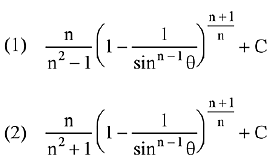
Ans. (1)
Solution.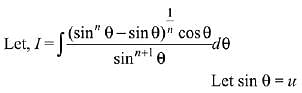
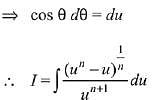
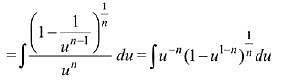

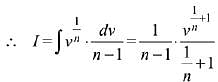
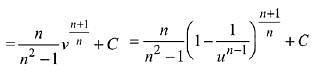

Q.6.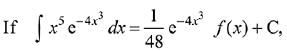 where C is a constant of integration, then f (x) is equal to: (2019)
where C is a constant of integration, then f (x) is equal to: (2019)
(1) - 2x3 - 1
(2) - 4x3 - 1
(3) -2x3 + 1
(4) 4x3+ 1
Ans. (2)
Solution. 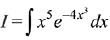
Put -4x3 = θ
⇒ -12x2 dx = dθ
⇒ 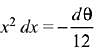
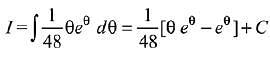
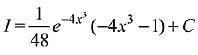
Then, by comparison
f(x) = -4x3 - 1
Q.7.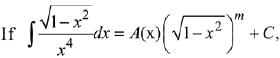 for a suitable chosen integer m and a function A (x), where C is a constant of integration, then (A(x))m equals: (2019)
for a suitable chosen integer m and a function A (x), where C is a constant of integration, then (A(x))m equals: (2019)
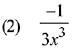
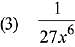
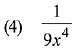
Ans. (1)
Solution.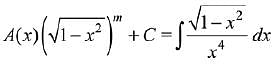
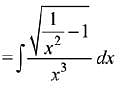
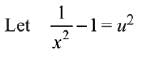
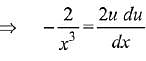
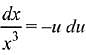
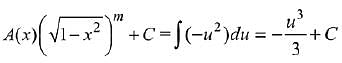
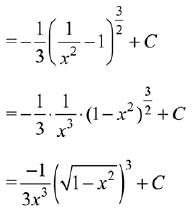
Comparing both sides,
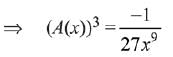
Q.8.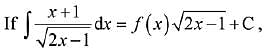 where C is a constant of integration, then f(x) is equal to: (2019)
where C is a constant of integration, then f(x) is equal to: (2019)
(1) 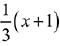
(2) 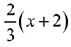
(3) 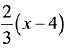
(4) 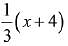
Ans. (4)
Solution.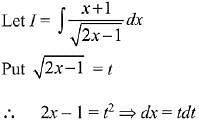
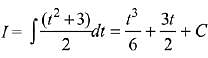
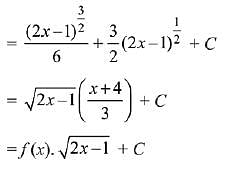
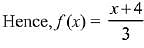
Q.9. The integral 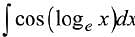 is equal to:
is equal to:
(where C is a constant of integration) (2019)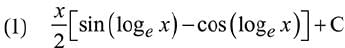
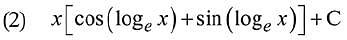
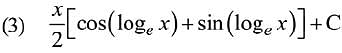
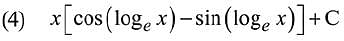
Ans. (3)
Solution.

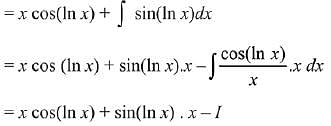
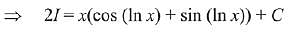
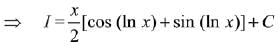
Q.10. The integral 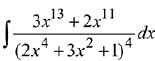 is equal to: (where C is a constant of integration) (2019)
is equal to: (where C is a constant of integration) (2019)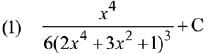
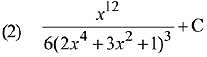
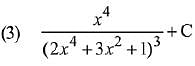
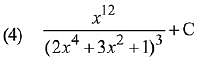
Ans. (2)
Solution.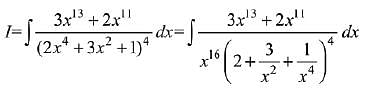
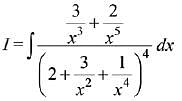
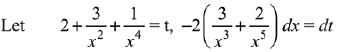
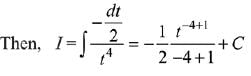
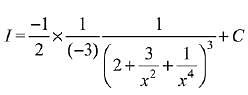
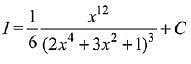
Q.11. 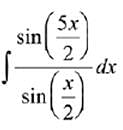 is equal to:
is equal to:
(where c is a constant of integration.) (2019)
(1) 2x + sinx + 2 sin2x + c
(2) x + 2 sinx + 2 sin2x + c
(3) x + 2 sinx + sin2x + c
(4) 2x + sinx + sin2x + c
Ans. (3)
Solution.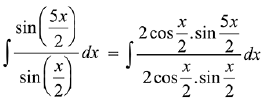
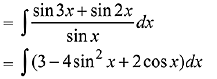
[ ∵ sin 2x = 2 sin x cos x and sin 3x = 3 sin x - 4 sin3x]
Q.12.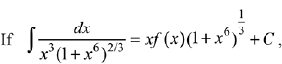 where C is a constant of integration, then the function f(x) is equal to: (2019)
where C is a constant of integration, then the function f(x) is equal to: (2019)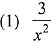
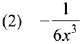
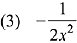
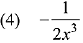
Ans. (4)
Solution.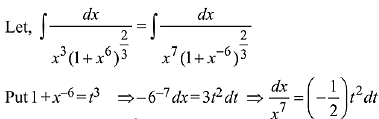
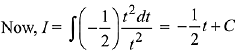
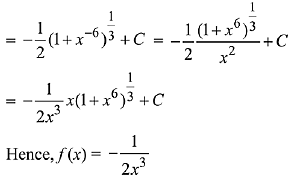
Q.13. The integral ∫ sec2/3 x cosec4/3 xdx is equal to:
(1) -3 tan-1/3 x + C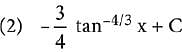
(3) -3 cot-1/3 x + C
(4) 3 tan-1/3 x + C
(Here C is a constant of integration) (2019)
Ans. (1)
Solution.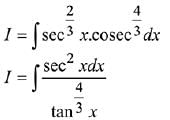
Q.14. If ∫esec x (sec x tan x f(x) + (sec x tan x + sec2 x)) dx = esecx f(x) + C, then a possible choice of f(x) is: (2019)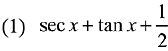
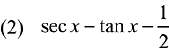
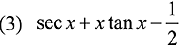

Ans. (1)
Solution.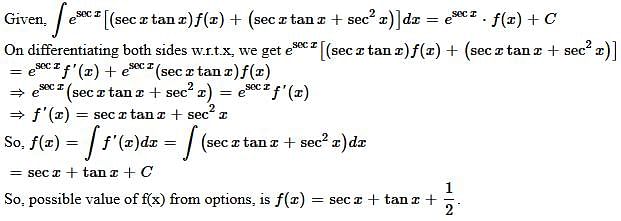
Q.15. where C is a constant of integration, then: (2019)
where C is a constant of integration, then: (2019)
(1) A = 1/54 and f(x) = 3 (x - 1)
(2) A = 1/81 and f(x) = 3 (x - 1)
(3) A = 1/27 and f(x) = 9 (x - 1)
(4) A = 1/54 and f(x) = 9 (x - 1)2
Ans. (1)
Solution.
Let (x - 1)2 = 9 tan2 θ ....(1)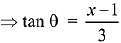
After differentiating equation ...(1), we get
2 (x - 1) dx = 18 tan θ sec2θ dθ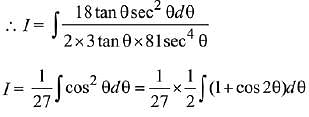

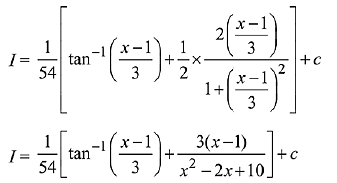
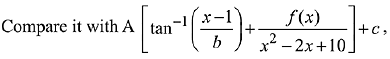
we get: A = 1/54 and f(x) = 3 (x - 1)
Q.16. If 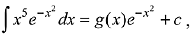 where c is a constant of integration, then g(-1) is equal to: (2019)
where c is a constant of integration, then g(-1) is equal to: (2019)
(1) -1
(2) 1
(3) 
(4) 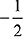
Ans. (3)
Solution.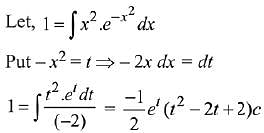
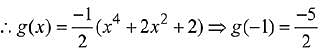
Q.17. The integral 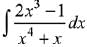 is equal to: (2019)
is equal to: (2019)
(Here C is a constant of integration)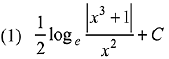
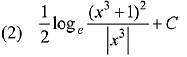


Ans. (3)
Solution.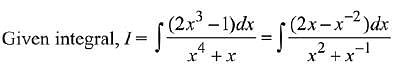
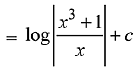
Q.18. Let α ∈ (0, π/2) be fixed. If the integral 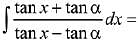 A(x) cos2α+B(x) sin2α+C, where C is a constant of integration, then the functions A(x) and B(x) are respectively: (2019)
A(x) cos2α+B(x) sin2α+C, where C is a constant of integration, then the functions A(x) and B(x) are respectively: (2019)
(1) x + α and loge|sin(x + α)|
(2) x - α and loge|sin(x - α)|
(3) x - α and loge |cos(x - α)|
(4) x + α and loge |sin(x - a)|
Ans. (2)
Solution.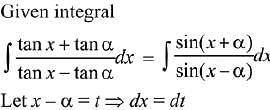
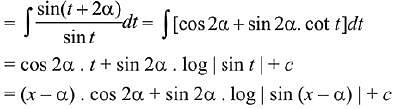
Q.19. The integral 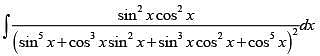 is equal to: (2018)
is equal to: (2018)
(1) 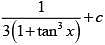
(2) 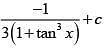
(3) 
(4) 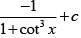
Ans. (2)
Solution.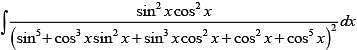

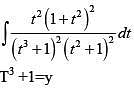

Q.20. If f 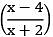 = 2x + 1, (x ∈ R − {1, −2}), then ∫ f(x)dx is equal to: (where C is a constant of integration) (2018)
= 2x + 1, (x ∈ R − {1, −2}), then ∫ f(x)dx is equal to: (where C is a constant of integration) (2018)
(1) 12 loge |1 - x| - 3x + C
(2) – 12 loge |1 – x| + 3x + C
(3) – 12 loge |1 – x| - 3x + C
(4) 12 loge |1 – x| + 3x + C
Ans. (3)
Solution.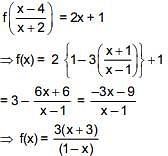
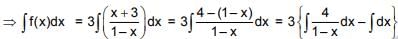
= 3 {–4ℓn|1–x – x| + C = –12ℓn |1–x| – 3x + C
Q.21. If f(x) = 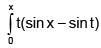 dt then: (2018)
dt then: (2018)
(1) f''' (x) - f''(x) = cosx - 2x sinx
(2) f'''(x) + f''(x) - f'(x) = cosx
(3) f'''(x) + f''(x) = sinx
(4) f'''(x) + f'(x) = cosx - 2x sinx
Ans. (4)
Solution.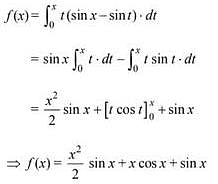

Q.22. If 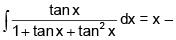
 (C is a constant of integration), then the ordered pair (K, A) is equal to (2018)
(C is a constant of integration), then the ordered pair (K, A) is equal to (2018)
(1) (2, 1)
(2) (2, 3)
(3) (–2, 1)
(4) (–2, 3)
Ans. (2)
Solution.
I = 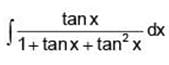
=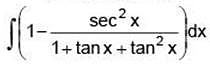
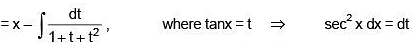
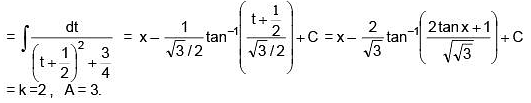
Q.23. Let In = ∫tann xdx,(n > 1). If I4 +I6= a tan5 x + bx5 + C, where C is a constant of integration, then the ordered pair (a, b) is equal to (2017)
(1) (-1/5 , 0)
(2) (-1/5 , 1)
(3) (1/5, 0)
(4) (1/5, -1)
Ans. (3)
Solution.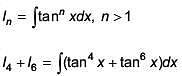
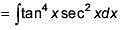
Let tanx = t
sec2x dx = dt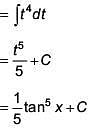
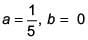
Q.24. The integral 
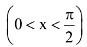 is equal to:
is equal to:
(where C is a constant of integration) (2017)
(1) 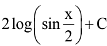
(2) 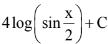
(3) 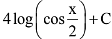
(4) 
Ans. (1)
Solution.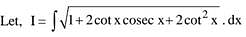


Q.25. If  and
and 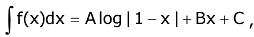 then the ordered pair (A,B) is equal to :(where c is a constant of integration) (2017)
then the ordered pair (A,B) is equal to :(where c is a constant of integration) (2017)
(1) 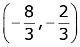
(2) 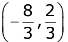
(3) 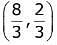
(4) 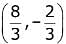
Ans. (2)
Solution.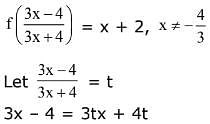

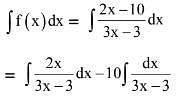
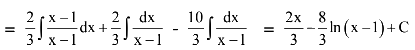
Q.26. The integral 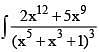 dx is equal to: (2016)
dx is equal to: (2016)
(1) 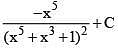
(2) 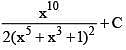
(3) 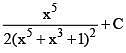
(4) 
Ans. (2)
Solution.
Dividing numerator and denominator by x15 we get,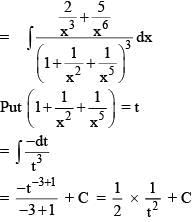
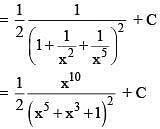
Q.27. If 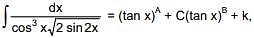 , where k is a constant of integration, then A + B + C equals (2016)
, where k is a constant of integration, then A + B + C equals (2016)
(1) 15/5
(2) 21/5
(3) 7/10
(4) 27/10
Ans. (1)
Solution.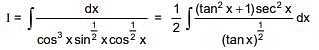
tan x = t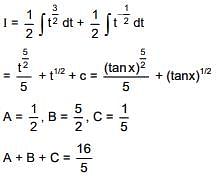
Q.28. The integral 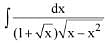 is equal to (where C is a constant of integration) (2016)
is equal to (where C is a constant of integration) (2016)
(1) 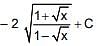
(2) 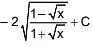
(3) 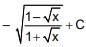
(4) 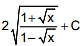
Ans. (2)
Solution.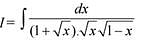
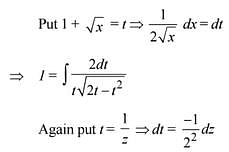
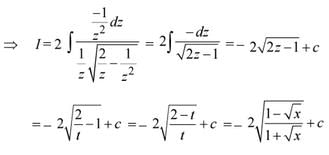
|
149 videos|192 docs|197 tests
|

|
Explore Courses for Airforce X Y / Indian Navy SSR exam
|

|


















