JEE Main Previous Year Questions (2016- 2025): Electromagnetic Induction & Alternating Current- 1 | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Q 1. A LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring-mass damped oscillator having damping constant b, the correct equivalence would be [2020]
Ans: (4)
Solution:
Given LCR circuit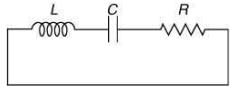
We know that equation of motion of damped oscillation is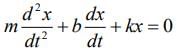 (1)
(1)
Now in the LCR circuit, voltage drop along the circuit is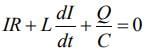
We know that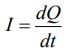
So
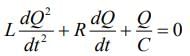 ..(2)
..(2)
Comparing Eqs. (1) and (2), we get
m = L , b= R, K = 1/C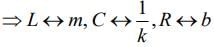
Q 2. An emf of 20 V is applied at time t = 0 to a circuit containing in series 10 mH inductor and 5 Ω resistor. The ratio of the currents at time t =∞ and t = 40 s is close to (Take e2 = 7.389)
(1) 1.06
(2) 1.15
(3) 1.46
(4) 0.84
Ans: (1)
Solution:
Given that, L = 10 mH = 10 × 10−3 H, R = 5 Ω, V = 20 V.
We know that, current at instant time t is given by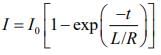
where
I0 = V/R = 20/5 = 4A
And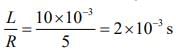
So,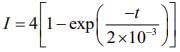
I = 4[1 - exp( - 500t )]
at t =∞, we have
I∞ = 4[1 - exp ( -∞] = 4(1-0) = 4
at t =40, we have
I40 = 4[1 - exp (-500 x 400)] = 4[1-exp (-20000)]
= 4[1-(e2)-10000] = 4[1 - (7.389)-10000]
So,
Therefore I∞/I40 is slightly greater than 1.
Q 3. As shown in the figure, a battery of emf ε is connected to an inductor L and resistance R in series. The switch is closed at t = 0. The total charge that flows from the battery, between t = 0 and t = tc (tc is the time constant of the circuit) is [2020]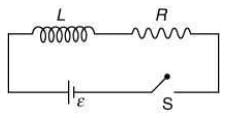
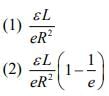
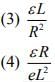
Ans: (1)
Solution:
Charge flow for time t1 to t2 is given by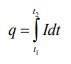
Here t1 = 0, t2 = tc
So,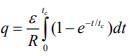
Current flow in the circuit at any instant t is given by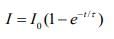
Here I0 = ε/R, τ = tc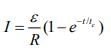
So,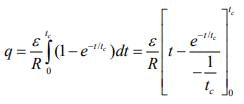
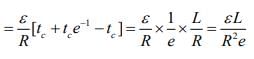
Q 4. In LC circuit the inductance L = 40 mH and capacitance C = 100 μF. If a voltage V(t) = 10 sin (314t ) is applied to the circuit, the current in the circuit is given as [2020]
(1) 0.52cos(314t)
(2) 10cos(314t)
(3) 5.2cos(314t)
(4) 0.52sin(314t)
Ans: (1)
Solution:
Given that LC series circuit having
L = 40mH = 40 x 10-3 H
C = 100μF = 100 x 10-6 F,
V(t) = 10sin (314t)
So,
ω = 314
XL = ωL = 314 x 40 x 10-3 = 12.56 Ω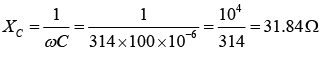
Z = XC - XL = 31.84 - 12.56 = 19.28 Ω
Since, XC > XL current lead the voltage by phase ϕ = π/2
Now, maximum current is given by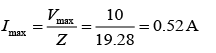
Therefore, current in the circuit is given by
Q 5. If the magnetic field in a plane electromagnetic wave is given by 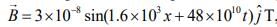 then what will be expression for electric field? [2020]
then what will be expression for electric field? [2020]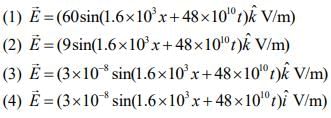
Ans: (2)
Solution:
Given that 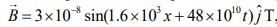
Standard equation of magnetic field of EM wave is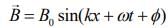
So,
B0 = 3 x 10-8, k = 1.6 x 103 , ω = 48 x 1010, ϕ = 0
we know that
E0 = B0 x c
= 3 x 10-8 x 3 x 108 = 9
Standard equation of electric field of EM wave is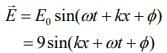
Therefore,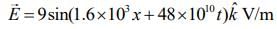
Q 6. The electric field of a plane electromagnetic wave is given by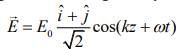
At t = 0, a positively charged particle is at the point(x ,y ,z ) = (0,0,π/k ). If its instantaneous velocity at (t = 0 ) is  the force acting on it due to the wave is [2020]
the force acting on it due to the wave is [2020]
(1) Parallel to 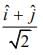
(2) zero
(3) antiparallel to 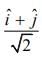
(4) parallel to 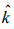
Ans: (3)
Solution:
Given that,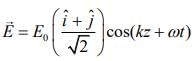
at t = 0, position of charged particle (x,y,z) 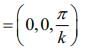
Instantaneous velocity, 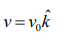
We know force is given by 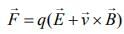
at t = 0, 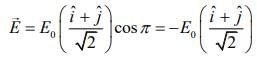
We know that speed of electromagnetic waves is given by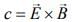
So, at t = 0,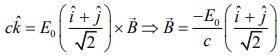

Therefore,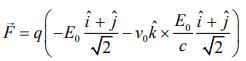
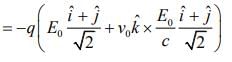
So, force is antiparallel to 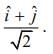
Q 7. A plane electromagnetic wave of frequency 25 GHz is propagating in vacuum along the z-direction. At a particular point in space and time, the magnetic field is given by 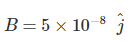 . The corresponding electric field
. The corresponding electric field 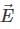 is (speed of light c = 3 x 108 m/s) [2020]
is (speed of light c = 3 x 108 m/s) [2020]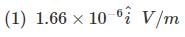
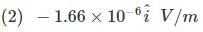
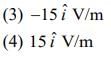
Ans: (4)
Solution:
given that,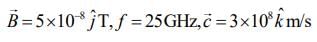
We know that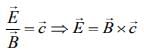
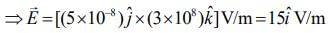
Q 8. The electric fields of two plane electromagnetic plane waves in vacuum are given by 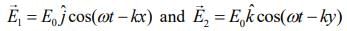 .
.
At t = 0, a particle of charge q is at origin with a velocity 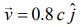 , (c is the speed of light in vacuum). The instantaneous force experienced by the particle is [2020]
, (c is the speed of light in vacuum). The instantaneous force experienced by the particle is [2020]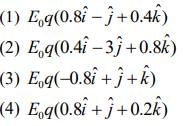
Ans: (4)
Solution:
Given that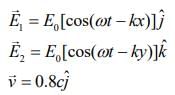
For given electric fields of electromagnetic waves, there corresponding magnetic fields are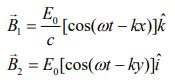
Force on a charge particle in these two electromagnetic waves is given by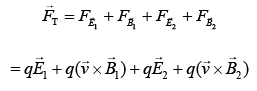
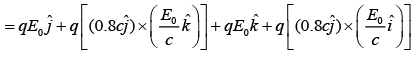
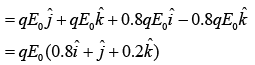
Q 9. A plane electromagnetic wave is propagating along the direction  with its polarization along the direction
with its polarization along the direction 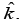 The correct form of the magnetic field of the wave would be (here B0 is an appropriate constant) [2020]
The correct form of the magnetic field of the wave would be (here B0 is an appropriate constant) [2020]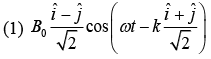
Ans: (1)
Solution:
Direction of propagation of EM wave is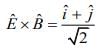
Direction of polarization of electric filed is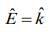
So, direction of polarization of magnetic field is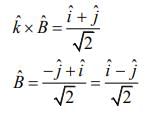
Therefore, direction of polarization of magnetic field is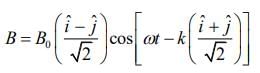
Q 10. A long solenoid of radius R carries a time (t) dependent current I(t) = I0t(1-t) with a ring of radius 2R is placed coaxially near its middle. During the time interval 0 ≤ t ≤ 1, the induced current (IR) and the induced EMF(VR) in the ring changes as [2020]
(1) Direction of IR remains unchanged and VR is maximum at t = 0.5 s
(2) At t = 0.25 s direction of IR reserves and VR is maximum
(3) Direction of IR remains unchanged and VR is zero at t = 0.25 s
(4) At t = 0.5 s direction of IR reverses and VR is zero
Ans: (4)
Solution:
Given that
I(t) = I0t(1-t)
Induced emf is given by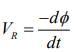
where ϕ is flux
Solenoid magnetic flux is given by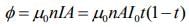
So,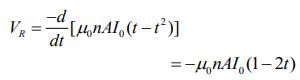
For t = 0.5 s, VR = 0
So emf will be zero at t = 0.5 s
At t = 0.5 s, direction of IR reverses and VR is zero.
Q 11. A planar loop of wire rotates in a uniform magnetic field. Initially, at t = 0, the plane of the loop is perpendicular to the magnetic field. If it rotates with a period of 10 s about an axis in its plane then the magnitude of induced emf will be maximum and minimum, respectively at [2020]
(1) 2.5 s and 7.5 s
(2) 2.5 s and 5.0 s
(3) 5.0 s and 7.5 s
(4) 5.0 s and 10.0 s
Ans: (2)
Solution:
We know, magnetic flux is given by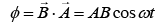
Where B is magnetic field and A is area
And emf induced is given by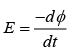
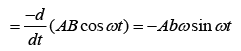
emf will be maximum when 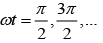
and emf will be minimum when ωt = π, 2π, ....
So, magnitude of induced emf will be maximum and minimum at 2.5 s and 5.0 s respectively.
Q 12. At time t = 0, magnetic field of 1000 Gauss is passing perpendicularly through the area defined by the closed loop shown in the figure. If the magnetic field reduces linearly to 500 Gauss, in the next 5 s, the induced EMF in the loop is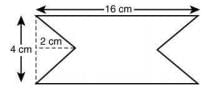 [2020]
[2020]
(1) 56 μV
(2) 28 μV
(3) 48 μV
(4) 36 μV
Ans: (1)
Solution:
Given that
B1 = 1000 Gauss = 1000 x 10-4 T
B2 = 500 Gauss = 500 x 10-4 T
t= 5s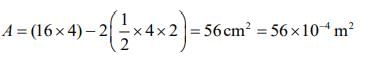
Induced EMF is given by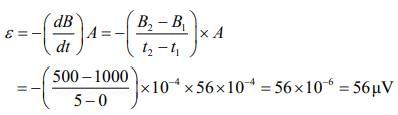
Q 13. In a fluorescent lamp choke (a small transformer), 100 V of reverse voltage is produced when the choke current changes uniformly from 0.25 A to 0 in a duration of 0.025 ms. The self-inductance of the choke (in mH) is estimated to be ________.
Ans: (10)
Solution:
Given that
V =100V, I1 = 0.25A, I2 = 0 A, t = 0.025 ms
Voltage across inductor is given by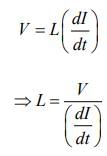
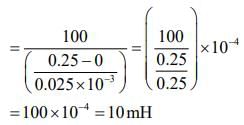
Q 14. A small circular loop of conducting wire has radius 'a' and carries current I. It is placed in a uniform magnetic field B perpendicular to its plane such that when rotated slightly about its diameter and released, it starts performing simple harmonic motion of time period T. If the mass of the loop is m then [2020]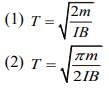
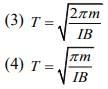
Ans: (3)
Solution:
Magnetic moment of circular loop carrying current I and radius a is given by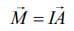
Where  is the area vector of the circular loop.
is the area vector of the circular loop.
Given conditions is shown in the following figure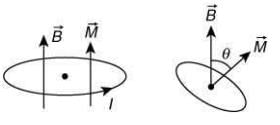
Torque on a current carrying circular loop in a magnetic field is given by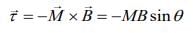
And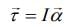
Where 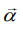 angular acceleration of the circular loop.
angular acceleration of the circular loop.
So, Iα = MBsin θ
For small θ , we have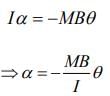
We know that, for SHM
α =-ω2θ
So,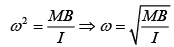
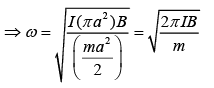
We know that
T = 2π/ω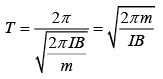
Q 15. A conducting circular loop made of a thin wire, has area 3.5 × 10−3 m2 and resistance 10 Ω. It is placed perpendicular to a time dependent magnetic field B(t) = (0.4 T) sin (50πt). The field is uniform in space. Then, the net charge flowing through the loop during t = 0 s and t = 10 ms is close to [2019]
(1) 14 mC
(2) 7 mC
(3) 21 mC
(4) 6 mC
Ans: (1)
Solution:
We have, A = 3.5 × 10−3 m2, R = 10 Ω
=(1/10) x 3.5 x 10-3 x 0.4
= 1.4 × 10−4 = 14 mC
Q 16. A solid metal cube of edge length 2 cm is moving in a positive y-direction at a constant speed of 6 m/s. There is a uniform magnetic field of 0.1 T in the positive z-direction. The potential difference between the two faces of the cube perpendicular to the x-axis, is [2019]
(1) 12 mV
(2) 6 mV
(3) 1 mV
(4) 2 mV
Ans: (1)
Solution:
Potential difference between two faces = E × l
= (v × B)l
= 6 × 0.1 × 2 × 10–2
= 12 mV
Q 17. There are two long coaxial solenoids of same length l. The inner and outer coils have radii r1 and r2 and number of turns per unit length n1 and n2, respectively. The ratio of mutual inductance to the self-inductance of the inner-coil is [2019]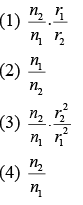
Ans: (4)
Solution:
Self-Inductance is
L = μ0n12πr12l [ϕ = Li]
Mutual inductance is
M = μ0n1n2πr12l [ϕ1 = Mi2]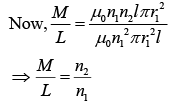
Q 18. A copper wire is wound on a wooden frame whose shape is that of an equilateral triangle. If the linear dimension of each side of the frame is increased by a factor of 3, keeping the number of turns of the coil per unit length of the frame the same, then the self-inductance of the coil [2019]
(1) decreases by a factor of 9.
(2) increases by a factor of 27.
(3) increases by a factor of 3.
(4) decreases by a factor of 9√3
Ans: (1)
Solution:
The self-inductance of the coil is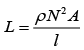
⇒ N/l = constant
⇒ N ∝ l
⇒ L ∝ lA
⇒ L ∝ la2
Therefore, self-inductance will increase by a factor of 3.
Q 19. A 10 m long horizontal wire extends from North East to South West. It is falling with a speed of 5.0 m/s, at right angles to the horizontal component of the Earth’s magnetic field, of 0.3 × 10−4 Wb/m2. The value of the induced emf in wire is [2019]
(1) 1.5 × 10−3 V
(2) 1.1 × 10−3 V
(3) 2.5 × 10−3 V
(4) 0.3 × 10−3 V
Ans: (2)
Solution:
Induced emf = Bvl sin θ
Since, θ = 45°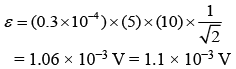
Q 20. A power transmission line feeds input power at 2300 V to a step-down transformer with its primary windings having 4000 turns. The output power is delivered at 230 V by the transformer. If the current in the primary of the transformer is 5 A and its efficiency is 90%, the output current would be [2019]
(1) 50 A
(2) 45 A
(3) 35 A
(4) 25 A
Ans: (2)
Solution:
Q 21. A series AC circuit containing an inductor (20 mH), a capacitor (120 μF) and a resistor (60 Ω) is driven by an AC source of 24 V/50 Hz. The energy dissipated in the circuit in 60 s is [2019]
(1) 5.65 × 102 J
(2) 2.26 × 103 J
(3) 5.17 × 102 J
(4) 3.39 × 103 J
Ans: (3)
Solution:
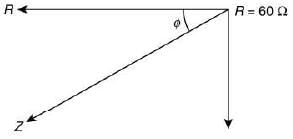
Given R = 60 Ω, f = 50 Hz, C = 120 μF = 120 × 10−6 F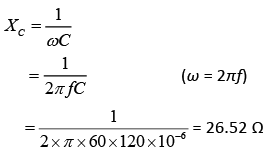
Inductive Reactance
XL = ωL
= 2πfL
= 2 × π × 50 × 20 × 10−3
= 6.28 Ω
Now,
XC – XL = 26.52 – 6.28
= 20.24
XC – XL ≈ 20
Impedance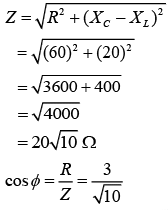
Power consumed by the AC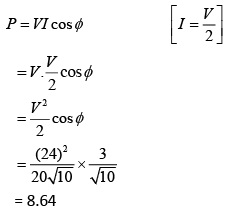
Hence, energy dissipated in the circuit in 60s = 5.17 × 102 J
Q 22. The self-induced emf of a coil is 25 volts. When the current in it is changed at uniform rate from 10 A to 25 A in 1 s, the change in the energy of the inductance is [2019]
(1) 740 J
(2) 437.5 J
(3) 540 J
(4) 637.5 J
Ans: (2)
Solution:
Induced emf,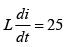
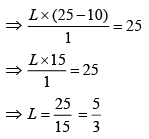
Therefore, change in energy of inductance is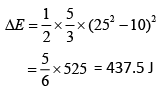
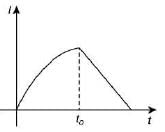
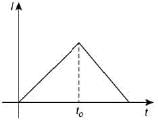
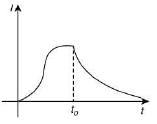
Q 23. In the circuit shown, the switch S1 is closed at time t = 0 and the switch S2 is kept open. At some later time "t0", the switch S1 is opened and S2, is closed. The behavior of the current I as a function of time t is given by [2019]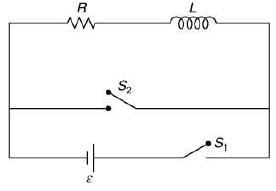
(1)
(2)
(3)
(4)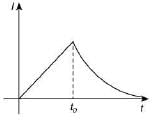
Ans: (N*)
*Disputed question – As more than one option is correct [options (1), (2), (4) are correct
Solution:
We have,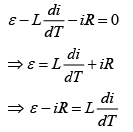
Now, integrating both the sides, we get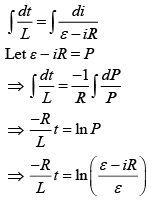

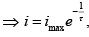 during decay
during decay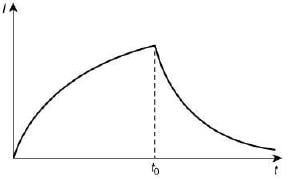
Q 24. In the figure shown, a circuit contains two identical resistors with resistance R = 5Ω and an inductance with L = 2 mH. An ideal battery of 15 V is connected in the circuit. What will be the current through the battery long after the switch is closed?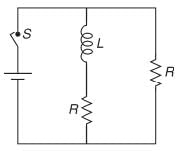 [2019]
[2019]
(1) 5.5 A
(2) 7.5 A
(3) 3 A
(4) 6 A
Ans: (4)
Solution: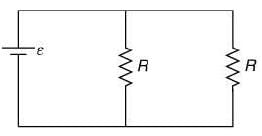
Let I be the current in the circuit.
Ideal inductor will behave like zero resistance long time after switch is closed.
I = 2E/R
⇒ I = (2 x 15) / 5
⇒ I = 6A
Q 25. In the circuit shown here, 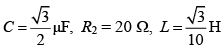 and R1 = 10 Ω. Current in L–R1 path is I1 and in C–R2 path it is I2. The voltage of AC source is given by V = 200√2 sin(100 t) volts. The phase difference between I1 and I2 is
and R1 = 10 Ω. Current in L–R1 path is I1 and in C–R2 path it is I2. The voltage of AC source is given by V = 200√2 sin(100 t) volts. The phase difference between I1 and I2 is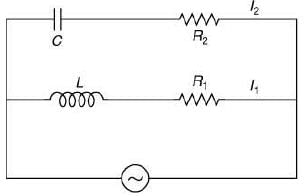 [2019]
[2019]
(1) 60°
(2) 30°
(3) 90°
(4) 0°
Ans: (3)
Solution:
Given V = 200√2 sin100t
ω = 100
XL = ωL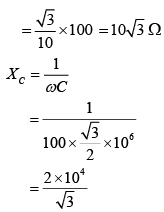
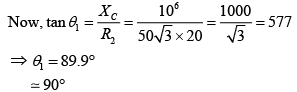
Thus, θ1 is close to 90°
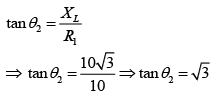
⇒θ2 = 60°
So, the phase difference = 90° + 60° = 150°
If R2 is 20 kΩ, then the phase difference = 60° + 30° = 90°.
Q 26. A plane electromagnetic wave of frequency 50 MHz travels in free space along the positive x direction. At a particular point in space and time, 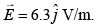 The corresponding magnetic field
The corresponding magnetic field 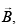 at that point will be [2019]
at that point will be [2019]
(1) 18.9 x 10-8 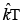
(2) 2.1 x 10-8 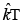
(3) 6.3 x 10-8 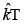
(4) 18.9 x 108 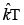
Ans: (2)
Solution:
Let  be the magnetic field, at a particular point
be the magnetic field, at a particular point 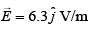
So,
where c is the speed of light.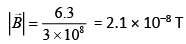
Unit vector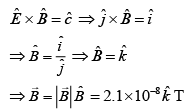
Q 27. The energy associated with electric field is ( UE) and with magnetic field is (UB) for an electromagnetic wave in free space. Then [2019]
(1) UB = UB/2
(2) UE > UB
(3) UE < UB
(4) UE = UB
Ans: (4)
Solution:
The average electric energy density is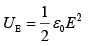
The average magnetic energy density is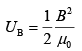
In electromagnetic wave, the electric and magnetic field vary sinusoidally in free space so, in above expression E and B are replaced by their rms values.
Therefore,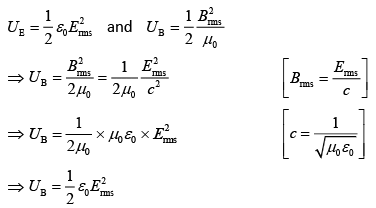
Since energy density of electric and magnetic field is equal.
Hence, UB = UE
Q 28. If the magnetic field of a plane electromagnetic wave is given by ( the speed of light = 3 × 108 m/s)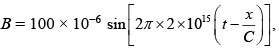 then the maximum electric field associated with it is [2019]
then the maximum electric field associated with it is [2019]
(1) 6 × 104 N/C
(2) 3 × 104 N/C
(3) 4 × 104 N/C
(4) 4.5 × 104 N/C
Ans: (2)
Solution:
speed of light is
c = 3 × 108 m/s
Magnetic field is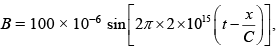
Maximum magnetic field, B0 = 100 × 10−6 T
Therefore, electric field is
E0 = c × B0
= 3 × 108 × 100 × 10−6
= 3 × 104 N/C
Q 29. The electric field of a plane polarized electromagnetic wave in free space at time t = 0 is given by an expression 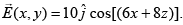 The magnetic field
The magnetic field 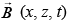 is given by (c is the velocity of light) [2019]
is given by (c is the velocity of light) [2019]
(1) 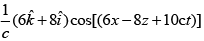
(2) 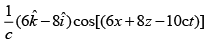
(3) 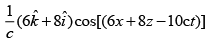
(4) 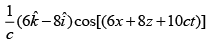
Ans: (2)
Solution:
Electric field is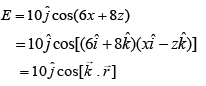
since, 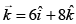 is direction of waves
is direction of waves
So, direction of 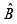 will be along
will be along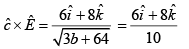
Let 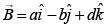 and unit vector in direction of propagation of EM wave is
and unit vector in direction of propagation of EM wave is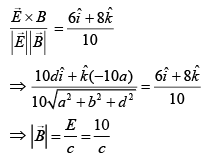
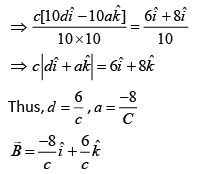
Therefore, 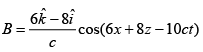
Q 30. An electromagnetic wave of intensity 50 W/m2 enters in a medium of refractive index ‘ n’ without any loss. The ratio of the magnitudes of electric fields, and the ratio of the magnitudes of magnetic fields of the wave before and after entering into the medium are respectively, given by [2019]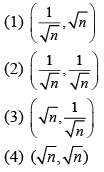
Ans: (3)
Solution:
As we know that,
For transparent medium
From Eq. (1) and Eq. (2), we have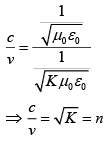
We know that, intensity in term of electric field is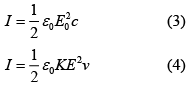
From Eq. (3) and Eq. (4), we have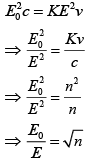
Similarly, in terms of magnetic field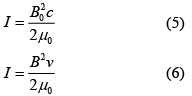
From Eq. (5) and Eq. (6), we get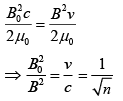
Q 31. A 27 mW laser beam has a cross-sectional area of 10 mm2. The magnitude of the maximum electric field in this electromagnetic wave is given by
(Given: Permittivity of space ε0 = 9x10-12 SI units; Speed of light c = 3 × 108 m/s.) [2019]
(1) 2 kV/m
(2) 0.7 kV/m
(3) 1 kV/m
(4) 1.4 kV/m
Ans: (4)
Solution:
Intensity of electromagnetic wave is given by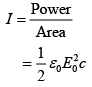
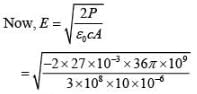
E = √2 x 103 V/m
E =1.4 kV/m
Q 32. In an a.c. circuit, the instantaneous e.m.f. and current are given by e = 100 sin 30 t 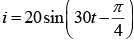 . In one cycle of a.c., the average power consumed by the circuit and the wattless current are, respectively: [2018]
. In one cycle of a.c., the average power consumed by the circuit and the wattless current are, respectively: [2018]
(1) 50, 10
(2) 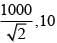
(3) 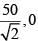
(4) 50, 0
Ans: (2)
Solution: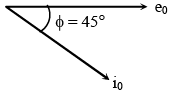
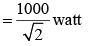
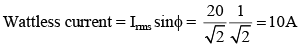
Q 33. For an RLC circuit driven with voltage of amplitude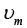 and frequency
and frequency 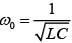 , the current exhibits resonance. The quality factor, Q is given by [2018]
, the current exhibits resonance. The quality factor, Q is given by [2018]
(1) 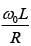
(2) 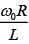
(3) 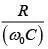
(4) 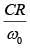
Ans: (1)
Solution: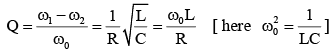
Alternate solution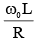 is the only dimensionless quantity, hence must be the quality factor.
is the only dimensionless quantity, hence must be the quality factor.
|
201 videos|410 docs|280 tests
|






















