Principal Ideal Domain | Algebra - Mathematics PDF Download
3.2 Principal Ideal Domains
Definition 3.2.1 A principal ideal domain (PID) is an integral domain in which every ideal is principal.
Lemma 3.2.2 Z is a PID.
NOTE: Showing that Z is a PID means showing that if I is an ideal of Z, then there is some integer n for which I consists of all the integer multiples of n.
Proof: Suppose that I ⊂ Z is an ideal. If I = {0} then I is the principal ideal generated by 0 and I is principal. If I ≠ {0} then I contains both positive and negative elements. Let m be the least positive element of I. We will show that I = (m).
Certainly (m) ⊂ I as I must contain all integer mulitples of m. On the other hand suppose a ∈ I. Then we can write
a = mq + r
where q ∈ Z and 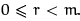 Then r = a - qm. Since a ∈ I and -qm ∈ I, this means r ∈ I. It follows that r = 0, otherwise we have a contradiction to the choice of m. Thus a = qm and a ∈ (m). We conclude I = (m).
Then r = a - qm. Since a ∈ I and -qm ∈ I, this means r ∈ I. It follows that r = 0, otherwise we have a contradiction to the choice of m. Thus a = qm and a ∈ (m). We conclude I = (m).
Note: In fact every subring of Z is an ideal - think about this.
Lemma 3.2.3 Let F be afield. Then the polynomial ring F[x] is a PID.
NOTE: Recall that F[x] has one important property in common with Z, namely a division algorithm. This is the key to showing that F[x] is a PID.
Proof: Let I ⊂ F[x] be an ideal. If I = {0} then I = (0) and I is principal. If I ≠ {0}, let f(x) be a polynomial of minimal degree m in I. Then (f(x)) ⊂ I since every polynomial multiple of f(x) is in I.
We will show that I = (f (x)). To see this suppose g(x) ∈ I. Then
g(x) = f(x)q(x) + r(x)
where q(x),r(x) ∈ F[x] and r(x) = 0 or deg(r(x)) < m. Now
r(x) = g(x) — f(x)q(x)
and so r(x) ∈ I. It follows that r(x) = 0 otherwise r(x) is a polynomial in I of degree strictly less than m, contrary to the choice of f(x).
Thus g(x) = f(x)q(x), g(x) ∈ (f(x)) and I = (f(x)).
Question for the Seminar: If R is a ring (not a field) it is not always true that R[x] is a PID.
Find an example of a non-principal ideal in Z[x].
|
161 videos|58 docs
|
FAQs on Principal Ideal Domain - Algebra - Mathematics
| 1. What is a principal ideal domain in mathematics? |  |
| 2. What are the key properties of principal ideal domains? |  |
| 3. How does a principal ideal domain differ from other types of rings? |  |
| 4. Can every integral domain be a principal ideal domain? |  |
| 5. How are principal ideal domains useful in mathematics? |  |

|
Explore Courses for Mathematics exam
|

|

















