Principle of Inclusion & Exclusion | Engineering Mathematics - Engineering Mathematics PDF Download
Principle of Inclusion and Exclusion and Derangement
- The principle of Inclusion and Exclusion is an approach that derives the method of finding the number of elements in the union of two finite sets. This is used for solving combinations and probability problems when it is necessary to find a counting method, which makes sure that an object is not counted twice.
- Consider two finite sets A and B. We can denote the Principle of Inclusion and Exclusion formula as follows.
n(A⋃B) = n(A) + n(B) – n(A⋂B) - Here n(A) denotes the cardinality of set A, n(B) denotes the cardinality of set B and n(A⋂B) denotes the cardinality of (A⋂B). We have included A and B and excluded their common elements.
The following figure gives you more idea on this.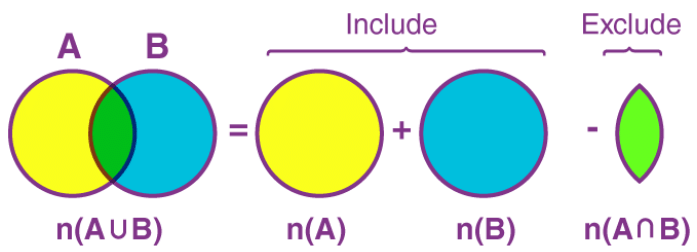
- If we have 3 sets A, B, and C, then according to the Principle of Inclusion and Exclusion, n(A⋃B⋃C) = n(A) + n(B) + n(C) – n(A⋂B) – n(A-C) – n(BC) + n(A⋂B⋂C)
- The principle of Inclusion and Exclusion represented by a Venn diagram for 3 sets is given below.
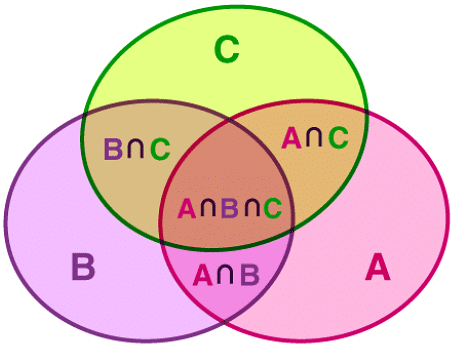
In general,
n(A1 ⋃ A2 ⋃ A3 ⋃….⋃ An) = Σn(Ai ⋂ Aj) + Σn(Ai ⋂ Aj ⋂ Ak) – ….+ (-1)n-1 n(A1 ⋂ A2 ⋂ A3 ⋂ …⋂An)
Derangement
The number of rearrangements, if n things are arranged in a row, such that none of them will occupy their original positions are called Derangements. We denote the number of derangements of n distinct things by Dn.
Dn = n![1 – (1/1!) + (1/2!) – (1/3!) + …. + (-1)n(1/n!)] where n≥2
Solved Examples of the Principle of Inclusion-Exclusion and Derangement
Example 1: Among a group of students, 49 study Physics, 37 study English and 21 study Biology. If 9 of these students study Maths Physics and English, 5 study English and Biology, 4 study Physics and Biology and 3 study Physics, English and Biology, find the number of students in the group.
(a) 91
(b) 92
(c) 86
(d) none of these
Let P represent the number of students who study Physics, E represent the number of students who study English and B represent the number of students who study Biology.
Number of students in the group = n(P⋃E⋃B)
Given n(P) = 49, n(E) = 37, n(B) = 21
n(P⋂E) = 9
n(E⋂B) = 5
n(P⋂B) = 4
n(P⋂E⋂B) = 3
n(P⋃E⋃B) = n(P) + n(E) + n(B) – n(P⋂E) – n(E⋂B) – n(P⋂B) + n(P⋂E⋂B)
= 49 + 37 + 21 – 9 – 5 – 4 + 3
= 92
Option b is the answer.
Example 2: Find the number of ways that you can put 7 letters into their respective envelopes such that exactly 3 go into the right envelope.
(a) 350
(b) 102
(c) 315
(d) 530
Number of ways in which the 3 correct envelopes can be selected= 7C3
= 7×6×5/1×2×3
= 35
Derangement of the remaining 4 envelopes and letters = 9 (derangement value for 4 is 9)
So the total number of ways of arrangement = 9 × 35= 315.
Option c is the answer.
|
65 videos|133 docs|94 tests
|





















