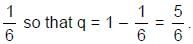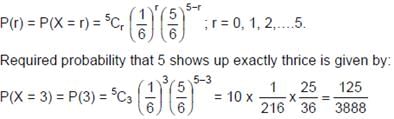Probability: Solved Examples- 1 | General Aptitude for GATE - Mechanical Engineering PDF Download
Introduction
Probability is one of the most important mathematical concepts that have a real presence & impact in our daily lives. There is a consistent presence of probability questions in CAT & other B school entrances at a min of 2 questions every year. This makes this chapter extremely important for an aspirant.
In this chapter, you intend to improve your concepts of probability to such an extent that you feel in total control of this topic through easy methods of explanations & practice examples.
What is Probability?
Probability is simply how likely something is to happen. Whenever you’re not certain about the outcome of an event, you can talk about the probabilities of certain outcomes—how likely they are.
Examples:
(i) The best example for understanding probability is flipping a coin
(ii) Probability (Chance) of rain on a given day.
(iii) Dice outcomes
- Whenever one is asked the question, what is the probability? the immediate question that arises/should arise in one’s mind is the probability of what?
The answer to this question is the probability of an EVENT. The EVENT is the cornerstone or the bottom line of probability. Hence, the first aspect of solving a question on probability is to define the event.
Probability of an Event
- If there are n-elementary events associated with a random experiment and m of them are favorable to an event A, then the probability of happening of A is denoted by P (A) and is defined as the ratio m/n.
- Probability of an event occurring =

- Thus, P (A) = m/n
Clearly, 0 ≤ m ≤ n, therefore 0 ≤ m/n ≤ 1, so that 0 ≤ P (A) ≤ 1
Tip:
a. Probability always lies between 0 and 1b. Probability of a sure event is 1
c. Probability is 0 for an impossible event
Example 1: Imagine an instance where you are throwing a dice, what is the probability of getting a number greater than 3, in a throw of a normal unbiased dice having 6 faces?
Here the event is throwing the dice at first place & condition of getting a number more than 3.
⇒ The event is defined as getting 4 or 5 or 6.
The individual probabilities of each of these are 1/6,1/6 and 1/6 respectively.
Hence, the required probability is 1/6 + 1/6 + 1/6 = 3/6 = 1/2.
Probability With the Use of Conjunctions AND and OR
In general, event definition means breaking up the event into the most basic building blocks, which are commonly through the two English conjunctions— AND and OR.
- ‘AND’ as a binding conjunctive
Whenever you see AND as the natural conjunction joining two separate parts of the event definition, you can replace the AND with the multiplication (x) sign.
Thus, if E AND R have to occur, and if the probability of their occurrence is P(E) and P(R) respectively, then the probability that E AND R occur is obtained by connecting P(E) AND P(R) i.e. replacing the AND by multiplication sign you get the required probability as:
Req Probability = P(E) x P(R) - ‘OR’ as a binding conjunctive
Whenever you see OR as the natural conjunction joining two separate parts of the event definition, you can replace the OR with the addition (+) sign.
Thus, if E OR R have to occur, and if the probability of their occurrence is P(E) and P(R) respectively, then the probability that E OR R occurs is obtained by connecting P(E) OR P(R) i.e. replacing the OR by addition sign you get the required probability as:
Req Probability = P(E) + P(R) - Combination of ‘AND’ and ‘OR’
You would encounter where the event is defined as the probability of each sub-event within the broad event is calculated and all the sub-events are connected by Multiplication (for AND) or by Addition (for OR) to get the final solution.
Example 2: The probability of E hitting a target is 1/2, and that of R hitting the target is 1/5, then the probability that both hit the target if one shot is taken by both of them is?
The event here is that E hits the target AND R hits the target, both hitting the target. Hence the resulting probability = P(E) AND P(R) = P(E) x P(R)
Using the values given of P(E) & P(R),
P(E) x P(R) = 1/2 x 1/5 = 1/10
Tip: When both events are connected by ‘AND’, please remember to use multiplication of events.
(Note: Remember the above explanation, where you used Multiplication when both events are connected by conjunctive AND. That is the reason why you multiplied them.)
Example 3: The probability of E hitting a target is 1/2, and that of R hitting the target is 1/5, then the probability that both hit the target if one shot is taken by either of them is?
As you can see whether E OR R hits the target, the outcome is counted even if one of them hits the target.
Hence, resulting probability = P(E) OR P(R) = P(E) + P(R)
Using the values given of P(E) & P(R),
P(E) + P(R) = 1/2 + 1/5 = 7/10
Tip: Look for the language of the question, conjunction ‘OR’ is used to connect the events, which means that you need to add them up.
Unlike in example, 2 where the event will happen only with both E & R events occurring, here if any one of E, R events can occur.
Example 4: If two dice are thrown, what is the chance that the sum of the numbers is not less than 10?
Event Definition: The sum of the numbers is not less than 10 i.e. either 10 OR 11 OR 12.
⇒ P(E) = (6 AND 4) OR (4 AND 6) OR (5 AND 5) OR (6 AND 5) OR (5 AND 6) OR (6 AND 6)
= [(1/6) x (1/6)] + [(1/6) x (1/6)] + [(1/6) x (1/6)] + [(1/6) x (1/6)] + [(1/6) x (1/6)] + [(1/6) x (1/6)] = 6/36 = 1/6
Hence for the event of sum less than 10, P(E’) = 1 - P(E) = 1 - 1/6 = 5/6.
Tip: You can see that no matter how many broad sub-events the problem of probability have, it can always be broken up into its narrower parts, which can be connected by ANDs and ORs to get the event definition.
Important Consideration during Defining Events
While attempting the questions, you need to take into consideration certain activities/events. Questions in CAT exams usually have direct or indirect mentions of such events.
Event: Event refers to any outcome of an experiment that is independent of any other outcome and cannot occur simultaneously with another event.
Experiment: An action that can deliver some well-defined outcomes, is an experiment.
(i) Impossible event and certain event
- An impossible event has no chance of occurring.
If event A is impossible, then P(A) = 0. - A certain event is certain to occur.
If event A is certain, then P(A) = 1.
(ii) Random experiment
- An experiment whose outcome has to be among a set of events that are completely known but whose exact outcome is unknown is a random experiment.
- Example: Throwing of a dice, tossing of a coin
- Most questions on probability in CAT are based on random experiments.
Random Experiment gives one or more results under identical conditions.
E.g. a coin is tossed.
Example 5: A coin is tossed and a single 6-sided dice is rolled. Find the probability of getting a head on the coin and a 3 on the dice.
P(head) = 1/2, P(3) = 1/6
P (head and 3) = (1/2) x (1/6) = 1/12
(iii) Sample space
- This is defined in the context of a random experiment and denotes the set representing all the possible outcomes of the random experiment.
Example: Sample space when a coin is tossed is (Head, Tail). Sample space when a dice is thrown is (1, 2, 3, 4, 5, 6).]
(iv) Mutually Exclusive Events
- Two or more events are said to be mutually exclusive if these events cannot occur simultaneously.
- Two or more events are said to be compatible if they can occur simultaneously. Two events (A and B) are mutually exclusive if the intersection of two events is null or they have no common element i.e. A ∩ B = φ.
- Example: In drawing a card from a deck of 52 cards,
A: The event that it is red.
B: The event that it is black.
C: The event that it is a king.
In the above case events A and B are mutually exclusive but events B and C are not mutually exclusive or disjoint since they may have common outcomes. Representation of probability of A and B
Representation of probability of A and B Representation of probability of B and C
Representation of probability of B and C
(v) Equally likely events
- If two events have the same probability or chance of occurrence they are called equally likely events.
- Example: In a throw of a dice, the chance of 1 showing on the dice is equal to 2 is equal to 3 is equal to 4 is equal to 5 is equal to 6 appearing on the dice.
(vi) Exhaustive set of events
- A set of events that includes all the possibilities of the sample space is said to be an exhaustive set of events.
- Example: In a throw of dice the number is less than three or more than or equal to three.
Example 6: If a two-digit no. is selected at random. What is the probability of getting a number, which has both the digits the same?
The total 2 digit numbers are 10 to 99 ⇒ 90
Required numbers are 11, 22, - - - - - 99 ⇒ 9
Thus, probability = 9/90 = 1/10
(vii) Independent events
- An event is described as such if the occurrence of an event has no effect on the probability of the occurrence of another event.
- Example: If the first child of a couple is a boy, there is no effect on the chances of the second child being a boy.)
(viii) Conditional probability
- It is the probability of the occurrence of event A given that event B has already occurred. This is denoted by P(A|B).
- Example: The probability that in two throws of dice you get a total of 7 or more, given that in the first throw of the dices the number 5 had occurred.
Sum Rule
- If E and F are two mutually exclusive events, then the probability that either event E or event F will occur in a single trial is given by: P(E or F) or P (E ∪ F) = P(E) + P(F)
If the event is not mutually exclusive, thenthe probability that either event E or event F will occur in a single trial is given by:
P(E ∪ F) = P(E) + P(F) – P(E and F together)
P (neither E nor F) = 1 – P(E or F)
Multiplication Rule
- When two events, A and B, are independent, the probability of both occurring is: P(A and B) = P(A ∩ B) = P(A) × P(B)
Complement of an Event
- Since the number of cases in which the event A will not happen is n - m, therefore if
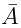 denotes not happening of A, then the probability P(
denotes not happening of A, then the probability P(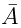 ) of not happening of A is given by:
) of not happening of A is given by: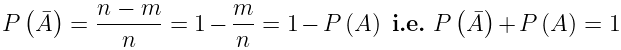
Example 7: From a bag containing 8 green and 5 red balls, three are drawn one after the other. Find the probability of all three balls being green if
(a) the balls drawn are replaced before the next ball is picked
(b) the balls drawn are not replaced.
(a) When the balls drawn are replaced, you can see that the number of balls available for drawing out will be the same for every draw.
⇒ The probability of a green ball appearing in the first draw and a green ball appearing in the second draw as well as one appearing in the third draw is equal to each other.
Hence, Required probability = (8/13) x (8/13) x (8/13) = (8/13)3
(b) When the balls are not replaced, the probability of drawing any color of ball for every fresh draw changes.
Hence, Required probability = 8/13 X 7/12 X 6/11
Tip: If n dice are thrown then total possible outcomes = 6n & if n coins are tossed then possible total outcomes = 2n
Binomial Probability Distribution
The Binomial Probability distribution is an experiment that possesses the following properties:
- There are a fixed number of trials which is denoted by n
- All the trials are independent.
- The outcome of each trial can either be a “success” or “failure”.
- The probability of success remains constant and is denoted by p.
The Binomial Probability distribution of exactly x successes from n number of trials is given by the below formula:
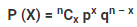
Where,
- n = Total number of trials
- x = Total number of successful trials
- p = probability of success in a single trial
- q = probability of failure in a single trial = 1-p
Example 8: A dice is tossed 5 times. What is the probability that 5 shows up exactly thrice?
Here the 'random experiment' consists of tossing a die 5 times and observing the number '5' as success,
⇒ p = Probability of getting '5' with single dice =
Since the value of p is constant for each dice and the trials are independent, using formula for Binomial probability law, the probability of r successes is given by:
Example 9: What is the chance of drawing an ace from a deck of cards?
There are 52 cards in a deck of cards, the total number of possible outcomes of drawing a card is 52.
Since there are 4 aces in a pack of cards, the total number of favorable outcomes is 4. The chance or probability of drawing an ace from the given pack = 4/52 = 1/13
Example 10: One card is drawn from a pack of 52 cards, each of the 52 cards being equally likely to be drawn. Find the probability that the card drawn is:
(i) an ace,
(ii) red,
(iii) either red or king,
(iv) red and a king
Out of 52 cards, one card can be drawn in 52C1 ways.
Therefore exhaustive number of cases = 52C1 = 52
(i) There are four aces in a pack of 52 cards, out of which one can be drawn in 4C1
Therefore Favourable number of cases = 4C1 = 4
So, required probability = 4/52 = 1/13
(ii) There are 26 red cards, out of which one red card can be drawn in 26C1 ways. Therefore, Favourable number of cases = 26C1 = 26
So, required probability = 26/52 = 1/2
(iii) There are 26 red cards including 2 red kings and there are 2 more kings. Therefore, there are 28 cards, one can be drawn in 28C1 ways.
Therefore favourable number of cases = 28C1 = 28
So, required probability = 28/52 = 7/13
(iv) There are 2 cards, which are red and king.
Therefore, favourable number of cases = 2C1 = 2.
So, required probability = 2/52 = 1/26.
Example 11: Harshad and Amit throw with two dice. If Harshad throws 10, what is Amit’s chance of throwing a higher number?
Total number of outcomes of throwing two dice is 6 × 6 = 36.
Amit must throw either 11 or 12.
This can be done in 3 ways namely (6 + 5, 5 + 6, 6 + 6)
Thus Amit’s chance of throwing a higher number is 3/36 or 1/12
Previous Year's Questions (Solved)
Q.1. In a throw of two dice, find the probability of getting one prime and one composite number.
(a) 1/2
(b) 1/3
(c) 2/3
(d) 3/4
Ans: B
Sol: The probability of getting a prime number (2,3 or 5) when a dice is thrown = 3/6 = 1/2.
The probability of getting a composite number (4 or 6) when a dice is thrown = 3/6 = 1/2.The event is— getting one prime and one composite number.
This can be got as first number prime and second composite OR first number composite and second prime = [(1/2) x (1/3)] + [(1/3) x (1/2)] = 1/3
EduRev Tip: ‘1’ is not a prime number.
Q.2. There are two bags containing white and black balls. In the first bag, there are 8 white and 6 black balls and in the second bag, there are 4 white and 7 black balls. One ball is drawn at random from any of these two bags. Find the probability of this ball being black.
(a) 40/77
(b) 41/77
(c) 37/77
(d) 43/77
Ans: B
Sol: The event definition: 1st bag and blackball OR 2nd Bag and Black Ball.
The chances of picking up either the 1st OR the 2nd Bag are 1/2 each.
The chance of picking up a black ball from the first bag is 6/14
The chance of picking up a black ball from the second bag is 7/11.Thus, using these values and the ANDs and ORs, Probability = [(1/2) x (6/14)] + [(1/2) x (7/11)] = (3/14) + (7/22) = (66 + 98)/(308) = 164/308 = 41/77
Q.3. An unbiased dice is thrown. What is the probability of getting
(i) an even number;
(ii) a multiple of 3;
(iii) an even number or a multiple of 3;
(iv) an even number & a multiple of 3?
Choose the most appropriate option.
(a) (1/3), (1/2), (2/3), (1/6)(b) (1/2), (1/3), (2/3), (1/6)(c) (1/2), (1/6), (2/3), (1/3)
(d) (1/6), (1/3), (2/3), (1/2)Ans: B
In a single throw of an unbiased dice, you can get any one of the outcomes 1, 2, 3, 4, 5, 6. So, the exhaustive number of cases = 6.
(i) An even number is obtained if you obtain any one of 2, 4, 6 as an outcome.
So, the favourable number of cases = 3.
Thus, required probability = (3/6) = (1/2)
(ii) A multiple of 3 is obtained if you obtain any one of 3, 6 as an outcome.
So, the favourable number of cases = 2.
Thus, required probability = (2/6) = (1/3)
(iii) An even number or a multiple of 3 is obtained in any of the following outcomes 2, 3, 4, 6. So, the favourable number of cases = 4.
Thus, required probability = (4/6) = (2/3)
(iv) An even number and a multiple of 3 are obtained if you get 6 as an outcome. So, the favourable number of cases = 1.
Thus, the required probability = (1/6)
|
193 videos|169 docs|152 tests
|
FAQs on Probability: Solved Examples- 1 - General Aptitude for GATE - Mechanical Engineering
| 1. What is probability? |  |
| 2. How do we use the conjunctions AND and OR in probability? |  |
| 3. What is an important consideration during defining events in probability? |  |
| 4. What is a binomial probability distribution? |  |
| 5. Can you provide an example of a solved probability problem? |  |