Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Problem Solving with Differentiation
Problem Solving with Differentiation | Mathematics for GCSE/IGCSE - Class 10 PDF Download
What problems could involve differentiation?
- Differentiation allows us to analyze how one quantity changes concerning another.
- The derived function, also known as the gradient function or derivative, provides a measure of the rate of change.
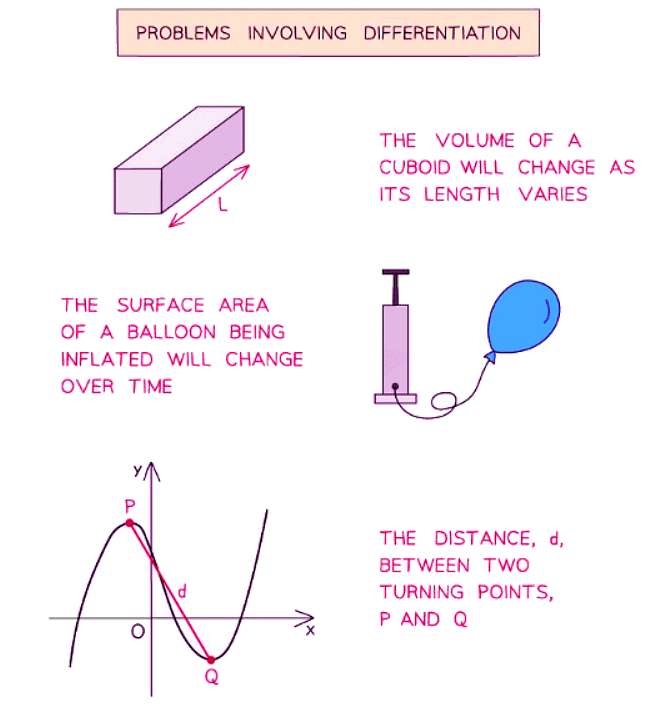
- Various problems involving a variable quantity can be addressed through differentiation. For instance:
- How the area of a rectangle changes as its length varies.
- How the volume of a cylinder changes as its radius varies.
- How the position of a car changes over time, indicating its speed.
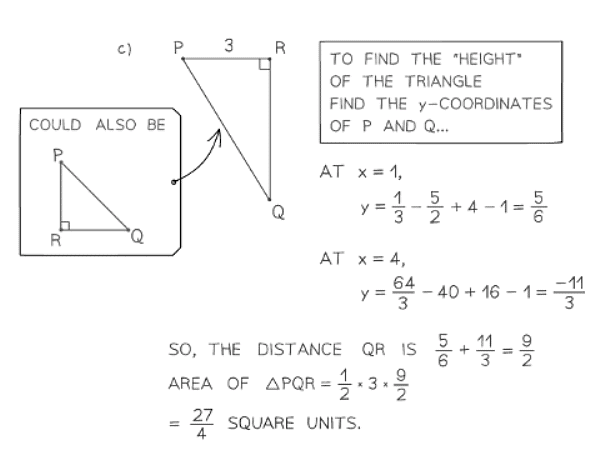
- Additionally, differentiation can be applied to problems based on the graph of a curve, such as determining:
- The distance between two turning points on the curve.
- The area of a shape formed by points on the curve, like turning points and axis intercepts.
How do I solve problems involving differentiation?
Problems generally fall into two categories:
1. Graph-based problems
- These problems are based around the graph of a curve and its turning points.
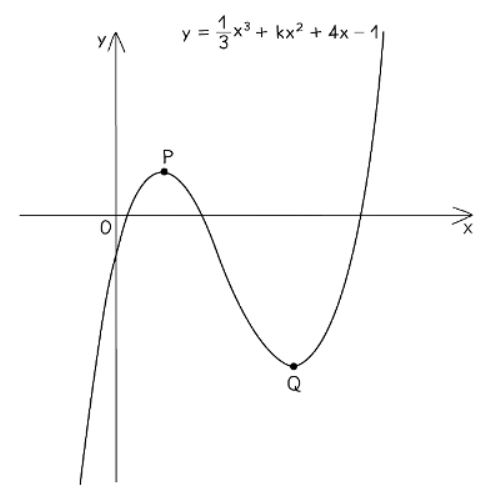
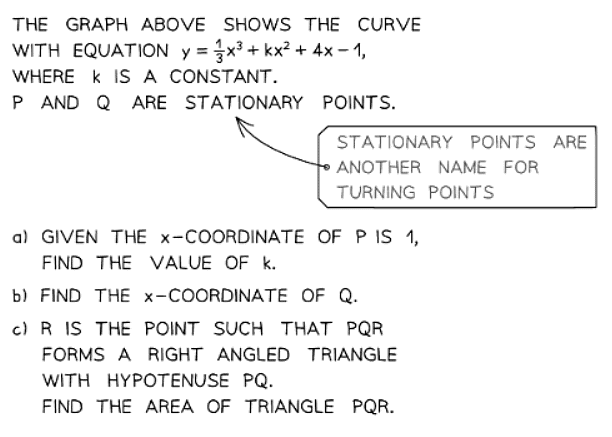
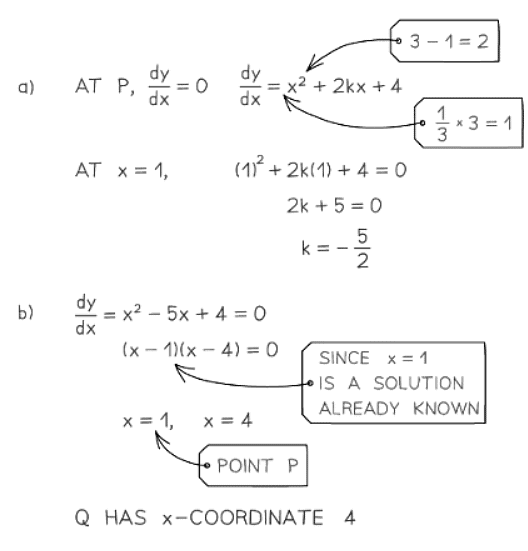
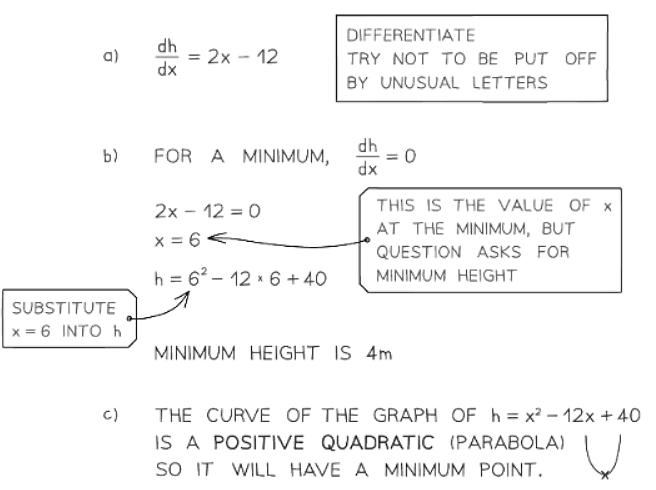
 2. Maximum/Minimum problems
2. Maximum/Minimum problems
- The maximum or minimum values hold significance in the context of the problem:
- For instance, the maximum volume of a box formed from a flat sheet of material or the minimum height of water in a reservoir.
- These scenarios are often referred to as optimization problems.
- The maximum or minimum value represents the optimal or best solution to the problem.

Question for Problem Solving with DifferentiationTry yourself: How can differentiation be applied to determine the maximum or minimum values in a problem?View Solution
The document Problem Solving with Differentiation | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
42 videos|395 docs|19 tests
|
FAQs on Problem Solving with Differentiation - Mathematics for GCSE/IGCSE - Class 10
| 1. What are some common problems that could involve differentiation? |  |
Ans. Some common problems that could involve differentiation include finding the maximum or minimum values of a function, determining rates of change, and calculating the slope of a curve at a specific point.
| 2. How can I solve problems involving differentiation? |  |
Ans. To solve problems involving differentiation, you first need to understand the basic rules of differentiation, such as the power rule, product rule, quotient rule, and chain rule. You then apply these rules to find the derivative of the given function and use it to solve the specific problem at hand.
| 3. How do I find the maximum or minimum values of a function using differentiation? |  |
Ans. To find the maximum or minimum values of a function using differentiation, you first find the critical points by setting the derivative equal to zero and solving for x. You then determine whether these critical points correspond to a maximum, minimum, or neither by using the second derivative test or analyzing the behavior of the function around these points.
| 4. What is the significance of rates of change in differentiation problems? |  |
Ans. Rates of change play a crucial role in differentiation problems as they help us understand how a function is changing at a particular point. By finding the derivative of a function, we can determine the rate at which the function is increasing or decreasing, which can be useful in various real-world applications such as physics, economics, and biology.
| 5. How can I calculate the slope of a curve at a specific point using differentiation? |  |
Ans. To calculate the slope of a curve at a specific point using differentiation, you first find the derivative of the function. Then, you substitute the x-coordinate of the point into the derivative to find the slope of the tangent line at that point, which represents the slope of the curve at that specific point.
Related Searches




















