Problems for Practice - 3 | Algebra - Mathematics PDF Download
For problems 1 & 2 use one of the Taylor Series derived in the notes to determine the Taylor Series for the given function.
1. Use one of the Taylor Series derived in the notes to determine the Taylor Series for f(x)=cos(4x) about x=0.
Solution. There really isn’t all that much to do here for this problem. We are working with cosine and want the Taylor series about x=0 and so we can use the Taylor series for cosine derived in the notes to get,
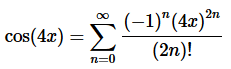
Step 2. Now, recall the basic “rules” for the form of the series answer. We don’t want anything out in front of the series and we want a single x with a single exponent on it.
In this case we don’t have anything out in front of the series to worry about so all we need to do is use the basic exponent rules on the 2x term to get,
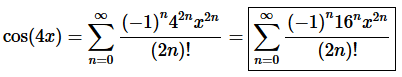
2. Use one of the Taylor Series derived in the notes to determine the Taylor Series for f(x)=x6e2x3 about x=0.
Solution. There really isn’t all that much to do here for this problem. We are working with the exponential function and want the Taylor series about x=0 and so we can use the Taylor series for the exponential function derived in the notes to get,
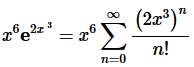
Note that we only convert the exponential using the Taylor series derived in the notes and, at this point, we just leave the x6 alone in front of the series.
Step 2. Now, recall the basic “rules” for the form of the series answer. We don’t want anything out in front of the series and we want a single x with a single exponent on it.
These are easy enough rules to take care of. All we need to do is move whatever is in front of the series to the inside of the series and use basic exponent rules to take care of the x
“rule”. Doing all this gives,
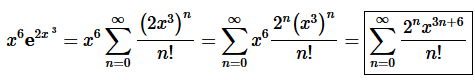
For problem 3 – 6 find the Taylor Series for each of the following functions.
3. Find the Taylor Series for f(x)=e−6x about x=−4.
Solution. Because we are working about x=−4 in this problem we are not able to just use the formula derived in class for the exponential function because that requires us to be working about x=0.
Step 2. So, we’ll need to start over from the beginning and start taking some derivatives of the function.
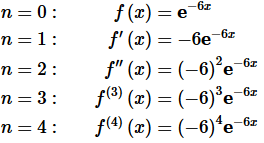
Remember that, in general, we’re going to need to go out to at least n=4
for most of these problems to make sure that we can get the formula for the general term in the Taylor Series.
Also, remember to NOT multiply things out when taking derivatives! Doing that will make your life much harder when it comes time to find the general formula.
Step 3. It is now time to see if we can get a formula for the general term in the Taylor Series.
In this case, it is (hopefully) pretty simple to catch the pattern in the derivatives above. The general term is given by,
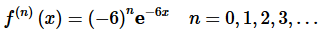
As noted this formula works all the way back to n=0. It is important to make sure that you check this formula to determine just how far back it will work. We will, on occasion, get formulas that will not work for the first couple of n’s and we need to know that before we start writing down the Taylor Series.
Step 4. Now, recall that we don’t really want the general term at any x. We want the general term at x=−4. This is,
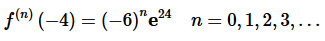
Step 5. Okay, at this point we can formally write down the Taylor Series for this problem.
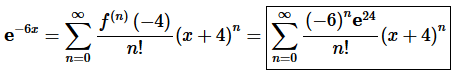
4. Find the Taylor Series for f(x)=ln(3+4x) about x=0.
Solution. Okay, we’ll need to start off this problem by taking a few derivatives of the function.
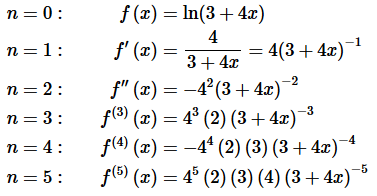
Remember that, in general, we’re going to need to go out to at least n=4
for most of these problems to make sure that we can get the formula for the general term in the Taylor Series.
Also, remember to NOT multiply things out when taking derivatives! Doing that will make your life much harder when it comes time to find the general formula. In this case we “merged” all the 4’s that came from the chain rule into a single term but left it as an exponent rather than get an actual value. This is not uncommon with these kinds of problems. The exponents we dropped down for the derivatives we left alone with the exception of dealing with the signs.
Step 2. It is now time to see if we can get a formula for the general term in the Taylor Series.
Hopefully you can see the pattern in the derivatives above. The general term is given by,
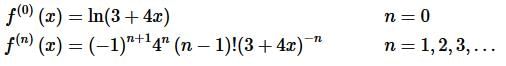
As noted this formula works all the way back to n=1 but clearly does not work for n=0. It is problems like this one that make it clear why we always need to check our proposed formula for the general solution to see just how far back it works.
Step 3. Now, recall that we don’t really want the general term at any x. We want the general term at x=0. This is,
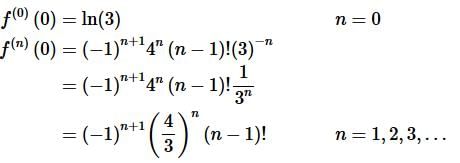
We did a little simplification for the second one just to make it a little simpler.
Step 4. Okay, at this point we can formally write down the Taylor Series for this problem. However, before we actually do that recall that our general term formula did not work for n=0 and so we’ll need to first strip that out of the series before we put the general formula in.
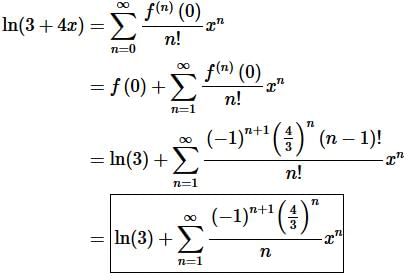
Don’t forget to simplify/cancel where we can in the final answer. In this case we could do some simplifying with the factorials.
5. Find the Taylor Series for 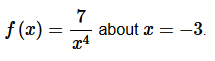
Solution. Okay, we’ll need to start off this problem by taking a few derivatives of the function.
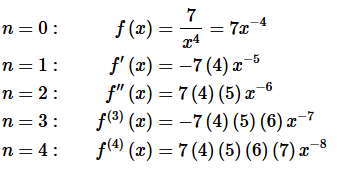
Remember that, in general, we’re going to need to go out to at least n=4
for most of these problems to make sure that we can get the formula for the general term in the Taylor Series.
Also, remember to NOT multiply things out when taking derivatives! Doing that will make your life much harder when it comes time to find the general formula. In this case the only “simplification” we did was to multiply out the minus signs that came from the exponents upon doing the derivatives. That is a fairly common thing to do with these kinds of problems.
Step 2. It is now time to see if we can get a formula for the general term in the Taylor Series.
Hopefully you can see the pattern in the derivatives above. The general term is given by,
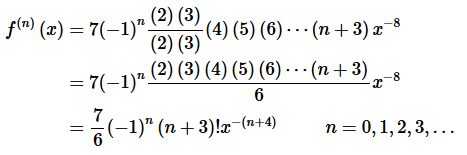
This formula may have been a little trickier to get. We almost had a factorial in the derivatives but each one was missing the (2)(3) part that would be needed to get the factorial to show up. Because that was all that was missing and it was missing in each of the derivatives we multiplied each derivative by 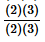 (i.e. a really fancy way of writing one…). We could then use the numerator of this to complete the factorial and the denominator was just left alone.
(i.e. a really fancy way of writing one…). We could then use the numerator of this to complete the factorial and the denominator was just left alone.
Also, as noted this formula works all the way back to n=0. It is important to make sure that you check this formula to determine just how far back it will work. We will, on occasion, get formulas that will not work for the first couple of n’s and we need to know that before we start writing down the Taylor Series.
Step 3. Now, recall that we don’t really want the general term at any x. We want the general term at x=−3. This is,
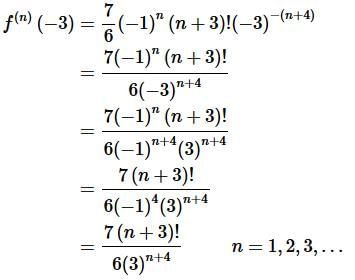
We did a little simplification here so we could cancel out all the alternating signs that were present in the term.
Step 4. Okay, at this point we can formally write down the Taylor Series for this problem.
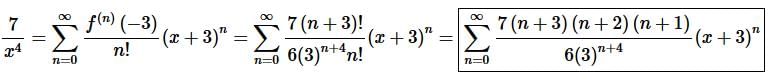
Don’t forget to simplify/cancel where we can in the final answer. In this case we could do some simplifying with the factorials.
6. Find the Taylor Series for f(x)=7x2−6x+1 about x=2.
Solution. First, let’s not get too excited about the fact that we have a polynomial here for this problem. It works exactly the same way with a few small differences.
We’ll start off by taking a few derivatives of the function and evaluating them at x=2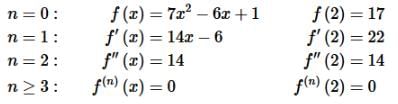
Okay, this is where one of the differences between a polynomial and the other types of functions we typically see with Taylor Series problems. After some point all the derivatives will be zero. That is not something to get excited about. In fact, it actually makes the problem a little easier!
Because all the derivatives are zero after some point we don’t need a formula for the general term. All we need are the values of the non-zero derivative terms.
Step 2. Once we have the values from the previous step all we need to do is write down the Taylor Series. To do that all we need to do is strip all the non-zero terms from the series and then acknowledge that the remainder will just be zero (all the remaining terms are zero after all!).
Doing this gives,
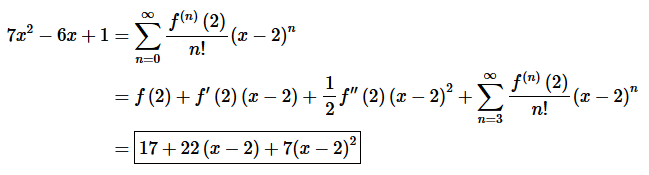
It looks a little strange but there it is. Do not multiply/simplify this out. This really is the answer we are looking for.
Also, don’t think that this is a problem that is just done to make you work another problem. There are applications of series (beyond the scope of this course however…) that really do require this kind of thing to be done as strange as that might sound!
|
161 videos|58 docs
|
FAQs on Problems for Practice - 3 - Algebra - Mathematics
| 1. How to solve quadratic equations? |  |
| 2. What is the difference between permutation and combination? |  |
| 3. How do you find the slope of a line? |  |
| 4. How to calculate the area of a circle? |  |
| 5. What is the Pythagorean theorem and how is it used? |  |

|
Explore Courses for Mathematics exam
|

|

















