Problems for Practice | Algebra - Mathematics PDF Download
End of Chapter Problems
Problem 1
Suppose that the universal set S is defined as S={1,2,⋯,10} and A={1,2,3}, B={X∈S:2≤X≤7}, and C={7,8,9,10}.
- Find A∪B
- Find (A∪C)−B
- Find A¯∪(B−C)
- Do A,B, and C form a partition of S?
Problem 2
When working with real numbers, our universal set is R. Find each of the following sets.
- [6,8]∪[2,7)
- [6,8]∩[2,7)
- [0,1]c
- [6,8]−(2,7)
Problem 3
For each of the following Venn diagrams, write the set denoted by the shaded area.
1. 
2. 
3. 
4. 
Problem 4
A coin is tossed twice. Let S be the set of all possible pairs that can be observed, i.e., S={H,T}×{H,T}={(H,H),(H,T),(T,H),(T,T)}. Write the following sets by listing their elements.
- A The first coin toss results in head.
- B At least one tail is observed.
- C The two coin tosses result in different outcomes.
Problem 5
Let A={1,2,⋯,100} For any i∈N, Define Ai as the set of numbers in A that are divisible by i. For example:
A2={2,4,6,⋯,100},
A3={3,6,9,⋯,99}.
- Find |A2|,|A3|,|A4|,|A5|
- Find |A2∪A3∪A5|
Problem 6
Suppose that A1, A2, A3 form a partition of the universal set S. Let B be an arbitrary set. Assume that we know
|B∩A1|=10,
|B∩A2|=20,
|B∩A3|=15.
Find |B|.
Problem 7
Determine whether each of the following sets is countable or uncountable.
- A={1,2,⋯,1010}
- B={a+b√2| a,b∈Q}
- C={(X,Y)∈R2|x2+y2≤1}
Problem 8


Find A.
Problem 9


Find A.
Problem 10
In this problem our goal is to show that sets that are not in the form of intervals may also be uncountable. In particular, consider the set A defined as the set of all subsets of N:
A={B:B⊂N}.
We usually denote this set by A=2N.
- Show that 2N is in one-to-one correspondence with the set of all (infinite) binary sequences:
C={b1,b2,b3,⋯|bi∈{0,1}}. - Show that C is in one-to-one correspondence with [0,1] .
From (a) and (b) we conclude that the set 2N is uncountable.
Problem 11
Show the set [0,1) is uncountable. That is you can never provide a list in the form of {a1,a2,a3,⋯} that contains all the elements in [0,1).
Problem 12
Recall that
{H,T}3 ={H,T}×{H,T}×{H,T}
={(H,H,H),(H,H,T),⋯,(T,T,T)}
Consider the following function
f:{H,T}3⟶N∪{0},
defined as
f(x)=the number of H's in x.
For example,
f(HTH)=2.
- Determine the domain and co-domain for f
- Find range of f :Range(f).
- If we know f(x)=2, what can we say about x?
Problem 13
Two teams A and B play a soccer match, and we are interested in the winner. The sample space can be defined as
S={a,b,d},
where a shows the outcome that A wins, b shows the outcome that B wins, and d shows the outcome that they draw. Suppose we know that:
(1) the probability that A wins is P(a)=P({a})=0.5;
(2) the probability of a draw is P(d)=P({d})=0.25
- Find the probability that B wins.
- Find the probability that B wins or a draw occurs.
Problem 14
Let A and B be two events such that P(A)=0.4,P(B)=0.7,P(A∪B)=0.9
- Find P(A∩B)
- Find P(Ac∩B)
- Find P(A−B)
- Find P(Ac−B)
- Find P(Ac∪B)
- Find P(A∩(B∪Ac))
Problem 15
I roll a fair die twice and obtain two numbers: X1= result of the first roll, X2= result of the second roll.
- Find the probability that X2=4
- Find the probability that X1+X2=7
- Find the probability that X1≠2 and X2≥4.
Problem 16
Consider a random experiment with a sample space
S={1,2,3,⋯}.
Suppose that we know:

where c is a constant number.
- Find c
- Find P({2,4,6})
- Find P({3,4,5,⋯}).
Problem 17
Four teams A,B,C,and D compete in a tournament, and exactly one of them will win the tournament. Teams A and B have the same chance of winning the tournament. Team C is twice as likely to win the tournament as team D. The probability that either team A or team C wins the tournament is 0.6. Find the probabilities of each team winning the tournament.
Problem 18
Let T be the time needed to complete a job at a certain factory. By using the historical data, we know that

- Find the probability that the job is completed in less than one hour, i.e., find P(T≤1)
- Find the probability that the job needs more than 2 hours.
- Find the probability that 1≤T≤3.
Problem 19
You choose a point (A,B) uniformly at random in the unit square {(x,y):x,y∈[0,1]}.

What is the probability that the equation
AX2+X+B=0
has real solutions?
Problem 20 (continuity of probability)
1. Let A1,A2,A3,⋯ be a sequence of increasing events, that is
A1⊂A2⊂A3⊂⋯
Show that

Using part(a), show that if A1,A2,⋯ is a decreasing sequence of events, i.e.,
A1⊃A2⊃A3⊃⋯
Then

Problem 21 (continuity of probability)
For any sequence of events A1,A2,A3,⋯, prove

Problem 22
Suppose that, of all the customers at a coffee shop,
- 70%purchase a cup of coffee;
- 40%purchase a piece of cake;
- 20%purchase both a cup of coffee and a piece of cake.
Given that a randomly chosen customer has purchased a piece of cake, what is the probability that he/she has also purchased a cup of coffee?
Problem 23
Let A,B, and C be three events with probabilities given below:

- Find P(A|B)
- Find P(C|B)
- Find P(B|A∪C)
- Find P(B|A,C)=P(B|A∩C)
Problem 24
A real number X is selected uniformly at random in the continuous interval [0,10]. (For example, X could be 3.87.)
- Find P(2≤X≤5)
- Find P(X≤2|X≤5)
- Find P(3≤X≤8|X≥4)
Problem 25
A professor thinks students who live on campus are more likely to get As in the probability course. To check this theory, the professor combines the data from the past few years:
- 600 students have taken the course,
- 120 students have gotten As,
- 200 students lived on campus,
- 80 students lived off campus and got As.
Does this data suggest that "getting an A" and "living on campus" are dependent or independent?
Problem 26
I roll a die n times, n∈N. Find the probability that numbers 1 and 6 are both observed at least once.
Problem 27
Consider a communication system. At any given time, the communication channel is in good condition with probability 0.8, and is in bad condition with probability 0.2. An error occurs in a transmission with probability 0.1 if the channel is in good condition, and with probability 0.3 if the channel is in bad condition. Let G be the event that the channel is in good condition and E be the event that there is an error in transmission.
1. Complete the following tree diagram:

2.Using the tree find P(E).
3. Using the tree find P(G|Ec).
Problem 28
In a factory there are 100 units of a certain product, 5 of which are defective. We pick three units from the 100 units at random. What is the probability that exactly one of them is defective?
Problem 29 Reliability
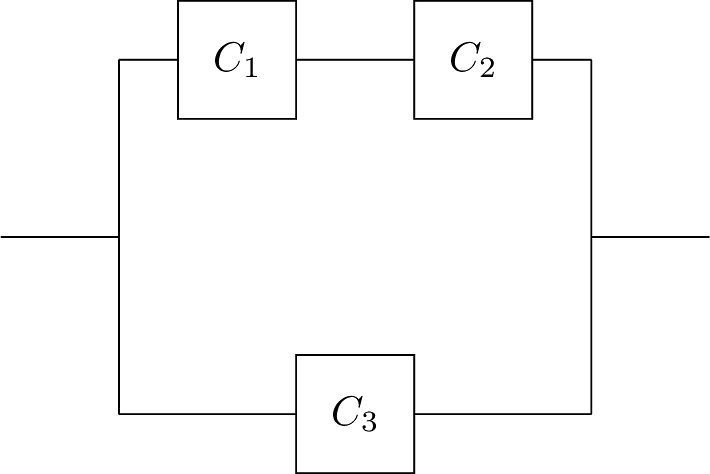
Real-life systems often are composed of several components. For example, a system may consist of two components that are connected in parallel as shown in Figure. When the system's components are connected in parallel, the system works if at least one of the components is functional. The components might also be connected in series as shown in Figure. When the system's components are connected in series, the system works if all of the components are functional.

In left figure, Components C1 and C2 are connected in parallel. The system is functional if at least one of the C1 and C2 is functional. In right figure, Components C1 and C2 are connected in series. The system is functional only if both C1 and C2 are functional.
For each of the following systems, find the probability that the system is functional. Assume that component k is functional with probability Pk independent of other components.
1.
2. 
3. 
4. 
5. 
Problem 30
You choose a point (X,Y) uniformly at random in the unit square
S={(x,y)∈R2:0≤x≤1,0≤y≤1}.
Let A be the event {(x,y)∈S:|x−y|≤1/2} and B be the event {(x,y)∈S:y≥x}.
- Show sets A and B in the x-y plane.
- Find P(A) and P(B).
- Are A and B independent.
Problem 31
One way to design a spam filter is to look at the words in an email. In particular, some words are more frequent in spam emails. Suppose that we have the following information:
- 50% of emails are spam;
- 1% of spam emails contain the word "refinance";
- 0.001% of non-spam emails contain the word "refinance".
Suppose that an email is checked and found to contain the word "refinance". What is the probability that the email is spam?
Problem 32
You would like to go from point A to point B in Figure 1.28. There are 5 bridges on different branches of the river as shown in Figure.

Bridge i is open with probability Pi, i=1,2,3,4,5. Let A be the event that there is a path from A to B and let Bk be the event that kth bridge is open.
- Find P(A).
- Find P(B3|A).
Problem 33 (The Monty Hall Problem)
You are in a game show, and the host gives you the choice of three doors. Behind one door is a car and behind the others are goats. You pick a door, say Door 1. The host who knows what is behind the doors opens a different door and reveals a goat (the host can always open such a door because there is only one door behind which is a car). The host then asks you: "Do you want to switch?" The question is, is it to your advantage to switch your choice?

Problem 34
I toss a fair die twice, and obtain two numbers X and Y. Let A be the event that X=2, B be the event that X+Y=7, and C be the event that Y=3.
- Are A and B independent?
- Are A and C independent?
- Are B and C independent?
- Are A , B, and C are independent?
Problem 35
You and I play the following game: I toss a coin repeatedly. The coin is unfair and P(H)=p. The game ends the first time that two consecutive heads (HH) or two consecutive tails (TT) are observed. I win if (HH) is observed and you win if (TT) is observed. Given that I won the game, find the probability that the first coin toss resulted in head?
Problem 36
A box contains two coins: a regular coin and one fake two-headed coin (P(H)=1). I choose a coin at random and toss it n times. If the first n coin tosses result in heads, what is the probability that the (n+1)th coin toss will also result in heads?
Problem 37
A family has n children, n≥2. We ask the father: "Do you have at least one daughter?" He responds "Yes!" Given this extra information, what is the probability that all n children are girls? In other words, what is the probability that all of their children are girls, given that at least one of them is a girl?
Problem 38
A family has n children, n≥2. We ask from the father, "Do you have at least one daughter named Lilia?" He replies, "Yes!" What is the probability that all of their children are girls? In other words, we want to find the probability that all n children are girls, given that the family has at least one daughter named Lilia. Here you can assume that if a child is a girl, her name will be Lilia with probability α≪1 independently from other children's names. If the child is a boy, his name will not be Lilia.
Problem 39
A family has n children. We pick one of them at random and find out that she is a girl. What is the probability that all their children are girls?
|
161 videos|58 docs
|
FAQs on Problems for Practice - Algebra - Mathematics
| 1. What are the different branches of mathematics? |  |
| 2. How can I improve my problem-solving skills in mathematics? |  |
| 3. What is the importance of mathematics in everyday life? |  |
| 4. How can I overcome math anxiety and fear? |  |
| 5. What are some practical applications of mathematics in the real world? |  |

|
Explore Courses for Mathematics exam
|

|

















