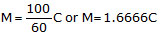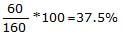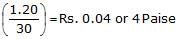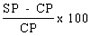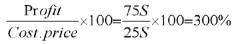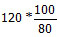Solved Examples: Profit, Loss & Discount | CSAT Preparation - UPSC PDF Download

Question 1: Alphonso, on his death bed, keeps half his property for this wife and divides the rest equally among his three sons: Ben, Carl and Dave. Some years later, Ben dies leaving half his property to his widow and a half to his brothers Carl and Dave together, sharing equally. When Carl makes his will, he keeps half his property for his widow and the rest he bequeaths to his younger brother Dave. When Dave dies some years later, he keeps half his property for his widow and the remaining for his mother. The mother now has Rs. 1,575,000.What was the worth of the total property?
(a) Rs. 30 lakh
(b) Rs. 8 lakh
(c) Rs. 18 lakh
(d) Rs. 24 lakh
Correct Answer is Option (d).
- Let the total property of the Alphonso be Rs.x.
- After Alphonso’s death, money possessed by the family members would be
Wife = x/2, Ben = x/6, Carl =x/6, Dave =x/6- After Ben’s death, money possessed by each of them would be
Alphonso’s wife = x/2, Ben = 0,Ben’s wife = x/6, Carl = x/6 + x/24 = 5x/24, Dave = x/6 + x/24 = 5x/24- After Carl’s death, money possessed by them, Alphonso’s wife has x/2, Ben has 0, Ben’s wife has x/12, Carl has 0, Carl’s wife has 5x/48, Dave has 5x/24 + 5x/48 = 15x/48
- After Dave’s death, money possessed by them is:
Alphonso’s wife has x/2 + 15x/96 = 63x/96, Ben has 0, Ben’s wife has x/12, Carl’s has 0, Carl’s wife has 5x/48, Dave has 0 and Dave’s wife has 15x/96
Now, given that 63x/96 = 1575000
x= 2400000
Alternative Method:
- You can also solve this question by using options.
- If we take the total amount to be Rs 2400000, then after Alphonso’s death, the money with the family members will be:
- Alphonso’s wife = 1200000, Ben = Carl = Dave = 400000, Ben will leave 100000 each for Carl and Dave.
- So, Carl and Dave have 50000 each, Carl will leave 250000 for Dave, so Dave has 750000.
- Dave left 750000/2 = 375000 for his mother, so his mother has 1200000 + 375000 = 1575000, which is given in the question. hence option 4 is the answer.
Question 2: Two oranges, three bananas and four apples cost Rs. 15. Three oranges, two bananas and one apple cost Rs. 10. I bought 3 oranges, 3 bananas and 3 apples. How much did I pay?
(a) Rs. 10
(b) Rs. 8
(c) Rs. 15
(d) Cannot be determined
Correct Answer is Option (c).
- It is given that
2O + 3B + 4A = 15 …..(1)
3O + 2B + A = 10…….(2)- The answer to this question seems to be cannot be determined as we are given three variables but we can form two equations only. But the question is not asking about the individual price of 3 oranges, 3 bananas and 3 apples but it asks the cost of 3O + 3B + 3A.
- For that, if we add the two equations, we get:
5O+5B+5A=25
O+B+A=5- Therefore 3O +3B+3A = 3×5 = 15
Question 3: A watch dealer incurs an expense of Rs. 150 for producing every watch. He also incurs an additional expenditure of Rs. 30,000, which is independent of the number of watches produced. If he is able to sell a watch during the season, he sells it for Rs. 250. If he fails to do so, he has to sell each watch for Rs. 100. If he produces 1500 watches, what is the number of watches that he must sell during the season in order to break even, given that he is able to sell all the watches produced?
(a) 500
(b) 700
(c) 800
(d) 1000
Correct Answer is Option (b).
- Total cost to produce 1500 watches = (1500 × 150 + 30000) = Rs. 2,55,000
- Let he sells x watches during the season, therefore number of watches sold after the season = (1500 – x)
- ∴Revenue earned on the sale of 1500 watches
= 250 × x + (1500 – x) × 100 = 150x + 150000- Now, break-even is achieved if the production cost is equal to the selling price.
∴ 150x + 150000 = 2,55,000 ⇒x = 700
Question 4: A stockist wants to make some profit by selling sugar. He contemplates various methods. Which of the following would maximize his profit?
1. Sell sugar at 10% profit.
2. Use 900 g of weight instead of 1 kg.
3. Mix 10% impurities in sugar and selling sugar at cost price.
4. Increase the price by 5% and reduce weights by 5%.
(a) I or III
(b) II
(c) II, III and IV
(d) Profits are the same
Correct Answer is Option (b).
- We will solve this question by taking all the cases one by one.
- In the first case, it is given that the profit is 10%.
- For the second case, let the CP of 1 kg of sugar be Rs. 100
Then CP of 900 g of sugar= (100/1000 )x 900 = Rs. 90
Hence, profit % in Case II= [{(100-90)/90}x100] = 11.11%- For case III, If he adds 10% impurity then his CP for 1 kg
= {(100/110) x 100} = Rs. 90.90
Hence, profit % in Case III = [{(100-90.90)/90.90} x 100] = 10.01%
and in the last case, If he reduces weight by 5%- Then cost price of 950 g = {(100/1000) x 950} = Rs. 95 and SP = Rs. 105
Hence, profit % in Case IV = {(105 – 95 )/95} X 100 = 10.52%- Hence, the profit is maximum in second case.
Question 5: A dealer offers a cash discount of 20% and still makes a profit of 20% when he further allows 16 articles to a dozen to a particularly sticky bargainer. How much per cent above the cost price were his wares listed
(a) 100%
(b) 80%
(c) 75%
(d) 66%
Correct Answer is Option (a).
- Let the CP of the article be Rs. x, since he earns a profit of 20%, hence SP = 1.2x.
It is given that he is selling 16 articles to a dozen, so he a incurs loss by selling 16 articles at the cost of 12 articles [loss = {(16-12)/16} x 100 = 25%]
∴ His selling price = SP × 0.75- Now SP × 0.75 = 1.2 x⇒ SP = (1.2/0.75)x = 1.6x.
This SP is arrived after giving a discount of 20% on MP.
Hence, MP = (1.6/0.8)x = 2x- It means that the article has been marked 100% above the cost price.
Alternative Method:
- Let the cost price = Rs 100. Since the profit is 20%, so the SP = Rs 120.
This SP = Rs 120 is arrived after giving a discount of 20%, i.e. MP = 120/0.8 = Rs 150.- Now he is selling 16 goods to a dozen, so his loss in this case = {(16-12)/16} x100 = 25%.
- It means that Rs 150 were arrived after losing 25%. Hence the actual MP = 150/0.75 = Rs 200.
- Hence, he has marked the MP 100% above the CP.
Question: 6 If a merchant offers a discount of 40% on the marked price of his goods and thus ends up selling at cost price, what was the % mark up?
(a) 28.57%
(b) 40%
(c) 66.66%
(d) 58.33%
Correct Answer is Option (c).
- If the merchant offers a discount of 40% on the marked price, then the goods are sold at 60% of the marked price.
- The question further states that when the discount offered is 40%, the merchant sells at cost price.
- Therefore, selling @ 40% discount = 60% of marked price (M) = cost price (C)
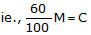
or
i.e., a mark up 66.66%
Question: 7 If a merchant offers a discount of 30% on the list price, then she makes a loss of 16%. What % profit or % loss will she make if she sells at a discount of 10% of the list price?
(a) 6% loss
(b) 0.8% profit
(c) 6.25% loss
(d) 8% profit
Correct Answer is Option (d).
- Let the cost price of the article be Rs.100 & Let the List price of the article be "x".
- Then, when the merchant offers a discount of 30%, the merchant will sell the article at x - 30% of x = 70% of x = 0.7x. .......(1)
Note: Discount is measured as a percentage of list price.- The loss made by the merchant when she offers a discount of 30% is 16%.
- Therefore, the merchant would have got 100 - 16% of 100 = Rs.84 when she offered a discount of 30%. .......(2)
Note: Loss is always measured as a percentage of cost price.- Therefore, equating equations (1) and (2), we get
0.7x = 84
or x = 120.- If the list price is Rs.120 (our assumption of cost price is Rs.100), then when the merchant offers a discount of 10%, she will sell the article at 120 - 10% of 120 = Rs.108.
- As the cost price of the article was Rs.100 and the merchant gets Rs.108 while offering a discount of 10%, she will make a profit of 8%.
Question: 8 A merchant marks his goods up by 60% and then offers a discount on the marked price. If the final selling price after the discount results in the merchant making no profit or loss, what was the percentage discount offered by the merchant?
(a) 60%
(b) 40%
(c) 37.5%
(d) Depends on the cost price
Correct Answer is Option (c).
- Assume the cost price to be 100.
- Therefore, the merchant's marked price will be 100 + 60% of 100 = 160
- Now, the merchant offers a discount on the marked price. The discount results in the merchant selling the article at no profit or loss or at the cost price.
- That is the merchant has sold the article at 100. Therefore, the discount offered = 60.
- The discount offered is usually measured as a percentage of the marked price.
Hence, % discount =
Question: 9 A merchant marks his goods up by 75% above his cost price. What is the maximum % discount that he can offer so that he ends up selling at no profit or loss?
(a) 75%
(b) 46.67%
(c) 300%
(d) 42.85%
Correct Answer is Option (d).
- Let us assume that the cost price of the article = Rs.100
- Therefore, the merchant would have marked it to Rs.100 + 75% of Rs.100 = 100 + 75 = 175.
- Now, if he sells it at no profit or loss, he sells it at the cost price i.e. he offers a discount of Rs.75 on his selling price of Rs.175
- Therefore, his % discount =
= 42.85%
Question: 10 A merchant marks his goods in such a way that the profit on the sale of 50 articles is equal to the selling price of 25 articles. What is his profit margin?
(a) 25%
(b) 50%
(c) 100%
(d) 66.67%
Correct Answer is Option (c).
- Let the selling price per article be = Re. 1
- Therefore, the selling price of 50 articles = Rs.50
- Profit on sale of 50 articles = selling price of 25 articles = Rs.25.
- S.P = 50. Profit = 25. Therefore, CP = 50 - 25 = 25.
.
Question: 11 Two merchants sell, each an article for Rs.1000. If Merchant A computes his profit on cost price, while Merchant B computes his profit on selling price, they end up making profits of 25% respectively. By how much is the profit made by Merchant B greater than that of Merchant A?
(a) Rs.66.67
(b) Rs.50
(c) Rs.125
(d) Rs.200
Correct Answer is Option (b).
- Merchant B computes his profit as a percentage of the selling price. He makes a profit of 25% on the selling price of Rs.1000. i.e. his profit = 25% of 1000 = Rs.250
Merchant A computes his profit as a percentage of cost price.- Therefore, when he makes a profit of 25% or 1/4th of his cost price, then his profit expressed as a percentage of selling price =
or 20% of the selling price.
- So, Merchant A makes a profit of 20% of Rs.1000 = Rs.200.
Merchant B makes a profit of Rs.250 and Merchant A makes a profit of Rs.200- Hence, Merchant B makes Rs.50 more profit than Merchant A.
Question: 12 One year payment to the servant is Rs. 200 plus one shirt. The servant leaves after 9 months and receives Rs. 120 and a shirt. What is the price of the shirt?
(a) Rs. 80
(b) Rs. 100
(c) Rs. 120
(d) Cannot be determined
Correct Answer is Option (c).
- The servant worked for 9 months instead of 12 months, he should receive 9/12 of his annual payment. Let the price of 1 shirt be Rs.S. i.e.,
.
- However, the question states that the servant receives Rs. 120 + S where S is the price of the shirt.
- By equating the two equations we get
= 120 + S.
Therefore Price of the shirt S = Rs. 120.
Question: 13 If apples are bought at the rate of 30 for a rupee. How many apples must be sold for a rupee so as to gain 20%?
(a) 28
(b) 25
(c) 20
(d) 22
Correct Answer is Option (b).
- The merchant makes a profit of 20%.
- This means that the merchant sells 30 apples for Rs.1.20
- Therefore, the selling price of 1 apple =
- The number of apples that can be sold for Rs.1.00 = Rs.
.
Question: 14 A trader buys goods at a 19% discount on the label price. If he wants to make a profit of 20% after allowing a discount of 10%, by what % should his marked price be greater than the original label price?
(a) +8%
(b) -3.8%
(c) +33.33%
(d) None of these
Correct Answer is Option (a).
- Let the label price be = Rs.100. The trader buys at a discount of 19%.
- Hence, his cost = 100 - 19 = 81.
- He wants to make a profit of 20%. Hence his selling price = 1.2 (81) = 97.2
- However, he wants to get this Rs.97.2 after providing a discount of 10%. i.e. he will be selling at 90% of his marked price.
- Hence, his marked price M =
= 108 which is 8% more than the original label price.
Question: 15 Rajiv sold an article for Rs.56 which cost him Rs.x. If he had gained x% on his outlay, what was his cost?
(a) Rs.40
(b) Rs.45
(c) Rs.36
(d) Rs.28
Correct Answer is Option (a).
- x is the cost price of the article and x% is the profit margin.
- Therefore, s.p =
= 56
=>= 56
So, 100x + x2 = 5600.- Solving for 'x' , we get x = 40 or x = -140. As the price cannot be a -ve quantity, x = 40. The cost price is 40 and the markup is 40.
- It is usually easier to solve such questions by going back from the answer choices as it saves a considerable amount of time.
Question: 16 A trader professes to sell his goods at a loss of 8% but weighs 900 grams in place of a kg weight. Find his real loss or gain per cent.
(a) 2% loss
(b) 2.22% gain
(c) 2% gain
(d) None of these
Correct Answer is Option (b).
- The trader professes to sell his goods at a loss of 8%.
- Therefore, Selling Price = (100 - 8)% of Cost Price
or SP = 0.92CP- But, when he uses weights that measure only 900 grams while he claims to measure 1 kg. Hence, CP of 900gms = 0.90 * Original CP
- So, he is selling goods worth 0.90CP at 0.92CP
Therefore, he makes a profit of 0.02 CP on his cost of 0.9 CP
Profit % =
i.e.,or 2.22%.
Question: 17 A merchant buys two articles for Rs.600. He sells one of them at a profit of 22% and the other at a loss of 8% and makes no profit or loss in the end. What is the selling price of the article that he sold at a loss?
(a) Rs.404.80
(b) Rs.440
(c) Rs.536.80
(d) Rs.160
Correct Answer is Option (a).
- Let C1 be the cost price of the first article and C2 be the cost price of the second article.
- Let the first article be sold at a profit of 22%, while the second one is sold at a loss of 8%. We know, C1 + C2 = 600.
- The first article was sold at a profit of 22%. Therefore, the selling price of the first article = C1 + (22/100)C1 = 1.22C1
- The second article was sold at a loss of 8%. Therefore, the selling price of the second article = C2 - (8/100)C2 = 0.92C2.
- The total selling price of the first and second article = 1.22C1 + 0.92C2.
- As the merchant did not make any profit or loss in the entire transaction, his combined selling price of article 1 and 2 is the same as the cost price of article 1 and 2.
- Therefore, 1.22C1 + 0.92C2 = C1+C2 = 600
As C1 + C2 = 600, C2 = 600 - C1.- Substituting this in 1.22C1 + 0.92C2 = 600, we get
1.22C1 + 0.92(600 - C1) = 600
or 1.22C1 - 0.92C1 = 600 - 0.92*600
or 0.3C1 = 0.08*600 = 48
or C1 = 48/(0.3) = 160.
If C1 = 160, then C2 = 600 - 160 = 440.- The item that is sold at loss is article 2. The selling price of article 2 = 0.92*C2 = 0.92*440
= 404.80.
Alternative Way:
- When you actually solve this problem in CAT, you should be using the following steps only:
1.22C1 + 0.92C2 = C1+C2 = 600
1.22C1 + 0.92(600 - C1) = 600
C1 = 48/(0.3) = 160.
C2 = 600 - 160 = 440.- And the final step of the answer which is 0.92*440 which you should not actually compute. As two of the answer choices (b) and (c) are either 440 or more, they cannot be the answers.
- The last one is way too low to be 92% of 440, therefore, the answer should be choice (a).
Question: 18 A trader makes a profit equal to the selling price of 75 articles when he sold 100 of the articles. What % profit did he make in the transaction?
(a) 33.33%
(b) 75%
(c) 300%
(d) 150%
Correct Answer is Option (c).
- Let S be the selling price of 1 article.
Therefore, the selling price of 100 articles = 100 S. --(1)- The profit earned by selling these 100 articles = selling price of 75 articles = 75 S -- (2
We know that Selling Price (S.P.) = Cost Price (C.P) + Profit -- (3)- Selling price of 100 articles = 100 S and Profit = 75 S from (1) and (2). Substituting this in eqn (3), we get
100 S = C.P + 75 S. Hence, C.P = 100 S - 75 S = 25 S.
Profit % =- Typically, you should take about 25 to 30 seconds to crack a problem of this kind. In reality, you should not be writing down all the steps that I have used to explain the solution.
- You should probably be framing equation (c) directly and compute the last step. The rest of the steps should be done mentally as you read the question for the first time.
Question: 19 If a merchant makes a profit of 20% after giving a 20% discount, what should be his mark-up?
(a) 20%
(b) 40%
(c) 50%
(d) 60%
(e) 48%
Correct Answer is Option (c).
- Assume cost price = 100.
- As profit % = 20%, the profit made after the discount = 20% of 100 = Rs.20
So, selling price = Rs.120.- The merchant makes this profit of 20% after a discount of 20%.
- Therefore, he is selling at Marked price - 20% of marked price = 80% of marked price.
i.e., 80% of marked price = Rs.120
80/100 of marked price = 120
Or marked price =
Or Markup = 50%
Question: 20 The Maximum Retail Price (MRP) of a product is 55% above its manufacturing cost. The product is sold through a retailer, who earns 23% profit on his purchase price. What is the profit percentage (expressed in nearest integer) for the manufacturer who sells his product to the retailer? The retailer gives 10% discount on MRP.
(a) 31%
(b) 22%
(c) 15%
(d) 13%
(e) 11%
Correct Answer is Option (d).
Key Data
- The MRP of the product is 55% above its manufacturing cost.
- The retailer sells the product after offering a discount of 10% on the MRP.
- The retailer makes a 23% profit on his purchase price.
Useful Assumption
- In Profit Loss questions where all data is given in percentage terms, assume cost price to be 100. Let the manufacturing cost = 100
- The MRP of the product is 55% above its manufacturing cost
The MRP of the product = 100 + 55% of 100 = 155.- The retailer sells the product after offering a discount of 10% on the MRP
So, the retailer sells the product at 155 – 10% of 155 = 155 – 15.5 = 139.5- The retailer makes a 23% profit on his purchase price. Let the purchase price for the retailer be x.
- So, the retailer sells the product at x + 23% of x = 123% of x.
- Step to retailer sells the product @ 139.5 = 123% of x
1.23x = 139.5
(or) x = 139.5/1.23- Therefore, x = 113.4, x is the purchase price for the retailer. So, x has to be the selling price for the manufacturer.
- The manufacturer sold the product at 113.4. The cost to the manufacturer is 100. So, the profit made by the manufacturer is 13.4. Because we assumed the cost price to be 100, the manufacturer makes a 13.4% profit. Rounded to the nearest integer, it is 13%.
|
205 videos|264 docs|136 tests
|
FAQs on Solved Examples: Profit, Loss & Discount - CSAT Preparation - UPSC
| 1. What is the formula to calculate profit or loss? |  |
| 2. How is profit percentage calculated? |  |
| 3. What is the formula to calculate discount? |  |
| 4. How is discount percentage calculated? |  |
| 5. How can the selling price be calculated if the cost price and profit percentage are known? |  |