Properties of Materials | Civil Engineering SSC JE (Technical) - Civil Engineering (CE) PDF Download
| Table of contents |

|
| Metal's Property, Stress and Strain |

|
| Stress |

|
| Strain |

|
| True Stress and True Strain |

|
| Hooke's Law |

|
| Properties of Materials |

|
| Elongation |

|
Metal's Property, Stress and Strain
Stress and Strain is the first topic in Strength of Materials which consist of various types of stresses, strains and different properties of materials which are important while working on them.
Stress
When a material is subjected to an external force, a resisting force is set up in the component. The internal resistance force per unit area acting on a material is called the stress at a point. It is a tensor quantity having unit of N/m2 or Pascal.
Stress = Force/Area
Force(F) is expressed in Newton (N) and A, original area, in square meters (m2), the stress σ will be expresses in N/m2. This unit is called Pascal (Pa).
- As Pascal is a small quantity, in practice, multiples of this unit is used.
1 kPa = 103Pa = 103N/m2 (kPa = Kilo Pascal)
1 MPa = 106Pa = 106N/m2 = 1N/mm2 (MPa = Mega Pascal)
1 GPa = 109N/m2 (GPa = Giga Pascal)
Types of Stresses
- Normal stress
 Normal stress = Normal force/area (σn = Fn/A)
Normal stress = Normal force/area (σn = Fn/A) - Shear Stress

- Bulk Stress
 Bulk stress = normal in ward force/area (σb = P)
Bulk stress = normal in ward force/area (σb = P)
Strain
It is the deformation produced in the material due to simple stress. It usually represents the displacement between particles in the body relative to a reference length.
Types of Strains
- Normal Strain: The normal strain of a body is generally expressed as the ratio of total displacement to the original length.
 Normal strain = change in normal length/original normal length
Normal strain = change in normal length/original normal length
εn = δl/l
Since strain is m/m it is dimensionless.
It is of two types: Longitudinal strain and Lateral Strain
Longitudinal strain is the defined as the ratio of the change in length of the body due to the deformation to its original length in the direction of the force.
Lateral Strain is defined as the ratio of the change in length (breadth of a rectangular bar or diameter of a circular bar) of the body due to the deformation to its original length (breadth of a rectangular bar or diameter of a circular bar) in the direction perpendicular to the force.
Poisson's ratio(μ) = -(Lateral strain/Longitudinal strain) - Shear strain
 Note 1: The angle is in radians, not degrees. The volume of the solid is not changed by shear strain.
Note 1: The angle is in radians, not degrees. The volume of the solid is not changed by shear strain.
Shear strain = tangential dislacement/original normal length
εt = δt/f = y(rad) - Bulk Strain or Volumetric Strain
 Bulk Strain = -(change in volume)/original volume
Bulk Strain = -(change in volume)/original volume
εB = -δV/V
Stress and Strain both are tensor quantity i.e. it has both change in magnitude as well as direction.
True Stress and True Strain
- The true stress is defined as the ratio of the load to the cross section area at any instant.
(σT) = load/Instantaneous area = σ(1 + ε)
Where σ and ε is the engineering stress and engineering strain respectively. - The true strain is defined as

Lo- original length, L-successive values of the length as it changes - The volume of the specimen is assumed to be constant during plastic deformation.
Stress-Strain Relationship
- The stress-strain diagram is shown in the figure. In brittle materials, there is no appreciable change in the rate of strain. There is no yield point and no necking takes place.


- In figure (a), the specimen is loaded only upto point A, when load is gradually removed the curve follows the same path AO and strain completely disappears. Such a behaviour is known as the elastic behaviour.
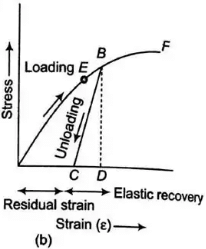
- In figure (b), the specimen is loaded upto point B beyond the elastic limit E. When the specimen is gradually loaded the curve follows path BC, resulting in a residual strain OC or permanent strain.
Comparison of engineering stress and the true stress-strain curves shown below:
The true stress-strain curve is also known as the flow curve.
- True stress-strain curve gives a true indication of deformation characteristics because it is based on the instantaneous dimension of the specimen.
- In engineering stress-strain curve, stress drops down after necking since it is based on the original area.
- In true stress-strain curve, the stress however increases after necking since the cross sectional area of the specimen decreases rapidly after necking.
- The flow curve of many metals in the region of uniform plastic deformation can be expressed by the simple power law.
σT = K(εT)n
Where K is the strength coefficient
- n is the strain hardening exponent
- n = 0 perfectly plastic solid
- n = 1 elastic solid For most metals, 0.1< n < 0.5
Hooke's Law
According to Hooke’s law the stress is directly proportional to strain i.e. normal stress (σ) ∝ normal strain (ε) and shearing stress ( ζ ) ∝ shearing strain ( γ ).
σ = Eε and ζ = γG
The co-efficient E is called the modulus of elasticity i.e. its resistance to elastic strain. The coefficient
G is called the shear modulus of elasticity or modulus of rigidity.
Properties of Materials
Some properties of materials which judge the strength of materials are given below:
- Elasticity: Elasticity is the property by virtue of which a material is deformed under the load and is enabled to return to its original dimension when the load is removed.
- Plasticity: Plasticity is the converse of elasticity. A material in the plastic state is permanently deformed by the application of load and it has no tendency to recover. The characteristic of the material by which it undergoes inelastic strains beyond those at the elastic limit is known as plasticity.
- Ductility: Ductility is the characteristic which permits a material to be drawn out longitudinally to a reduced section, under the action of a tensile force (large deformation).
- Brittleness: Brittleness implies the lack of ductility. A material is said to be brittle when it cannot be drawn out by tension to the smaller section.

- Malleability: Malleability is a property of a material which permits the material to be extended in all directions without rapture. A malleable material possesses a high degree of plasticity, but not necessarily great strength. Malleability is a physical property of metals that defines their ability to be hammered, pressed, or rolled into thin sheets without breaking
- Toughness: Toughness is the property of a material which enables it to absorb energy without fracture
- Hardness: Hardness is the ability of a material to resist indentation or surface abrasion. Brinell hardness test is used to check hardness.
- Strength: The strength of a material enables it to resist fracture under load.
Engineering Stress-Strain Curve
- The stress-strain diagram is shown in the figure. The curve starts from an origin. Showing thereby that there is no initial stress of strain in the specimen.
- The stress-strain curve diagram for a ductile material like mild steel is shown in the figure below.
- * Upto point A, Hooke's Law is obeyed and stress is proportional to strain. Point A is called limit of proportionality.

- Point B is called the elastic limit point.
- At point B the cross-sectional area of the material starts decreasing and the stress decreases to a lower value to point D, called the lower yield point.
- The apparent stress decreases but the actual or true stress goes on increasing until the specimen breaks at point C, called the upper yield point
- From point E onwards, the strain hardening phenomena become predominant and the strength of the material increases thereby requiring more stress for deformation, until point F is reached. Point F is called the ultimate point.
Elongation
A prismatic bar loaded in tension by an axial force P  For a prismatic bar loaded in tension by an axial force P. The elongation of the bar can be determined as δ=PL/AE
For a prismatic bar loaded in tension by an axial force P. The elongation of the bar can be determined as δ=PL/AE
- Elongation of composite body
Elongation of a bar of varying cross section A1 ,A2 ,----------,An of lengths l1 , l2,--------ln respectively
- Elongation of a tapered body
 Uniformly tapering circular bar
Uniformly tapering circular bar
- Elongation of a body due to self weight
(i) Elongation of a uniform rod of length ‘L’ due to its own weight ‘W’
δ = WL/2AE
The deformation of a bar under its own weight as compared to that when subjected to a direct axial load equal to its own weight will be half.
(ii) Total extension produced in rod of length ‘L’ due to its own weight ‘ ω ’ per with length.
δ = ωL2/2EA
(iii) Elongation of a conical bar due to its self weight
|
2 videos|122 docs|55 tests
|
FAQs on Properties of Materials - Civil Engineering SSC JE (Technical) - Civil Engineering (CE)
| 1. What are the properties of metals related to stress and strain? |  |
| 2. What is the difference between stress and strain in materials? |  |
| 3. How is true stress and true strain different from conventional stress and strain measurements? |  |
| 4. What is Hooke's Law and how does it relate to the properties of materials? |  |
| 5. How do properties of materials such as elongation affect their behavior under stress and strain? |  |
|
2 videos|122 docs|55 tests
|

|
Explore Courses for Civil Engineering (CE) exam
|

|
 Normal stress = Normal force/area (σn = Fn/A)
Normal stress = Normal force/area (σn = Fn/A)
 Bulk stress = normal in ward force/area (σb = P)
Bulk stress = normal in ward force/area (σb = P) Normal strain = change in normal length/original normal length
Normal strain = change in normal length/original normal length Note 1: The angle is in radians, not degrees. The volume of the solid is not changed by shear strain.
Note 1: The angle is in radians, not degrees. The volume of the solid is not changed by shear strain. Bulk Strain = -(change in volume)/original volume
Bulk Strain = -(change in volume)/original volume