Propositional & First Order logic | RRB JE for Computer Science Engineering - Computer Science Engineering (CSE) PDF Download
Propositions

A Proposition is a declarative sentence that is either TRUE or FALSE, but never both.
Examples:
- Delhi is the capital of India.
- 2 + 2 = 5
- 1 + 1 = 2
All the above are propositions as they can be true or false but not both.
Some examples of sentences that are not propositions:
- 1 + x = 5.
- It will rain tomorrow.
All the above examples are not propositions, they can be either be true or false.
Negation of Proposition
The negation operator is a unary operator which, when applied to a proposition p, changes the truth value of p. That is, the negation of a proposition p, denoted by ¬p, is the proposition that is false when p is true and true when p is false.
Example 1: Find out the negation of the proposition.
“Aman runs very fast.”
Solution: It is not the case that Aman runs very fast.
In simpler terms “Aman doesn't run fast”.
Example 2: Find out the negation of the proposition.
"It is raining outside."
Solution: Negation of p is- ∼p:
"It is not raining outside".
Disjunction
The disjunction is a connective that forms compound propositions that are false only if both statements (disjuncts) are false. It is denoted by p ∨ q, is the proposition ‘p or q’. The Disjunction p ∨ q is TRUE when anyone of p or q is TRUE.
Truth Table: Disjunction
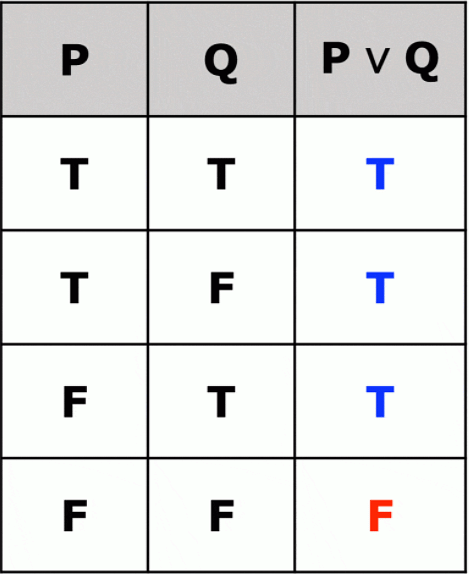
Example 1: If p and q are two propositions where-
p: 2 + 4 = 6 and q: It is raining outside
Solution: Then, the disjunction of p and q is -p ∨ q: 2 + 4 = 6 or it is raining outside.
Conjunction
A conjunction is a truth-functional connective similar to "and" in English and is represented in symbolic logic with " ^ ". The conjunction of p and q, denoted by p∧q, is the proposition ‘p and q’. The Conjunction p∧q is TRUE when both p and q are TRUE.
Truth Table: Conjunction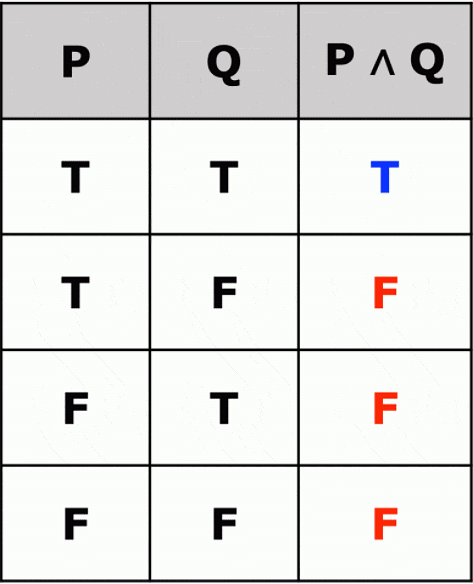
Logical Implication
It is a type of relationship between two statements or sentences. Denoted by ‘p → q’.
In English implication can be written as follows:
- if p then q ➜ p implies q
- if p, q ➜ p only if q
- q when p ➜ p is sufficient for q
The conditional statement p → q is false when p is true and q is false, and true otherwise.
Example 1: ‘if India wins, I will give party’.
Solution: Here p is India wins.
q is I will give a party.
Truth Table: Logical Implication
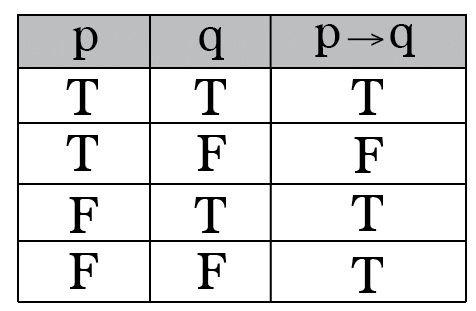
Bi-Condition
- A bi-conditional statement is a compound statement formed by combining two conditionals under “and.”
- Bi-conditionals are true when both statements have the exact same truth value.
In English, Bi-Conditional can be written as follows:
- p is necessary and sufficient for q.
- "if p then q" and "if q then p."
- p if and only if q
- p iff q
Truth Table: Bi-Condition

Propositional Equivalences
- Tautology: A compound proposition that is always true.
- Contradiction: A compound proposition that is always false.
- Contingency: A compound statement that is neither true or neither false under every possible value. A contingency is neither a Tautology nor a Contradiction. In other words, a formula is a contingency if the formula and its complement both are satisfiable (There exist an entry in the truth table for which the compound formula is true and there also exist an entry for which false)
Examples:
Let ‘p’ be a compound proposition
- p ∨¬p is a tautology.
- p ∧¬p is a contradiction.
- x > 4 is contingency as it can be true for some values
and false for some values.
Logical Equivalences
Those compound propositions which have the same truth values in all possible cases are known as Logical Equivalences.
Denoted by ‘≡’ or ‘⇔’ symbol.
Example 1. Show that p → q and ¬p ∨ q are equivalent.
Solution. We can construct a truth table to show equivalence.

As seen from the Truth table, ‘p → q’ and ‘¬p ∨ q’ have the same truth values. So we can say p → q ≡ ¬p ∨ q.
Some Useful Equivalence


Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Predicates
- A predicate is a Boolean-valued function on some variable(s).
- Let see some example predicates:
"x > 10"
"x = y + 3" - The first statement “x is greater than 10″ has two parts, “x” is the subject of the statement and “is greater than 10″ is the predicate. The statement “x is greater than 10″ can be denoted by P(x), where P denotes the predicate and x is the variable.
Example 1. Let P(x) denote the statement “x > 10″. What are the truth values of P(11) and P(5)?
Solution. P(11) means 11 > 10, which is TRUE.
P(5) means 5 > 10, which is FALSE.
Example 2. Let R(x,y) denotes the statement ” x = y + 1″. What is the truth value of the proposition R(1,3) and R(2,1) ?
Solution. R(1,3), 1 = 3 + 1 is FALSE. R(2,1), 2 = 1 + 1 is TRUE.
Quantifier
- In logic, quantification is a construct that specifies the number of specimens in the domain of discourse that satisfies an open formula.
Example: In arithmetic, it allows the expression of the statement that every natural number has a successor. - A language element that generates a quantification (such as “every”) is called a quantifier.
Universal Quantifier
- Universal Quantification of a predicate P(x) means
- P(x) for all values of x in its domain
‘∀’ is used to represent a universal quantifier.
Example 1. Let P(x) be the statement ” x + 2 > x” . What is the truth value of the ∀xP(x).
Solution. As x+2 is greater than x for any real number, so ∀xP(x) is always TRUE.
Existential Quantifier
- Existential Quantification of a predicate P(x) means
There exists an element x in the domain such that P(x). - ‘∃’ is known as an existential quantifier.
Example 1. Let P(x) be the statement “x>5″. What is the truth value of the ∃xP(x)?
Solution. For some real number such as x = 4, ∃xP(x) is also true.
Negating Quantified Expression
- ¬∀xP(x) ≡ ¬P(x)
- ¬∃xQ(x) ≡ ∀x ¬Q(x)
Solution. Let say H(x) denotes x as an honest man. So the statement can be written as ∃x H(x).
The negation of ∃x H(x) using the above results is ∀x ¬H(x).
Nested quantifier
Two quantifiers are nested if one is within the scope of the other.
Example 1. ∀x∃y(x + y = 0).
Solution. In the above example, we have two quantifiers ‘∀’ and ‘∃’ within the scope of each other.
In English, we can read it as ‘for all x, there exists a y for which x+y becomes 0.’
Example 2. Translate the following statement into English.
∀x∃y(x = -y), x and y belongs to real number.
Solution. For every real number x, there is a real number y such that x = -y.
Example 3. Translate the following statement into English.
∀x∀y((x > 0) ∧ (y > 0) → (x +y > 0)) ,Domain Real Numbers.
Solution. For two positive integers, the sum of these integers is positive.
OR in simpler terms, Sum of two positive numbers is positive.
Order of Quantifier
- Order of quantifier is important unless all quantifier is universal(∀) or all are existential(∃)
∀x∀y P(x,y) is the same as ∀y∀x P(x,y). - ∃x∃y Q(x,y) is the same as ∃y∃x Q(x,y).
- ∃y R(x,y) is not the same as ∀y∃x R(x,y).
Example 1. Translate the following into logical expressions.
“If a person is a student and is computer science major, then this person takes a course in mathematics.”
Solution.
- P(x) : x is student.
- Q(x) : x is computer science major.
- R(x,y) : x takes y course.
- ∀x (P(x) ∧ Q(x) ) → ∃y R(x,y).
|
12 videos|7 docs|103 tests
|
FAQs on Propositional & First Order logic - RRB JE for Computer Science Engineering - Computer Science Engineering (CSE)
| 1. What is propositional logic? |  |
| 2. What is the difference between a proposition and a predicate? |  |
| 3. What is the negation of a proposition? |  |
| 4. What is a logical implication? |  |
| 5. What is the difference between propositional and first-order logic? |  |
|
12 videos|7 docs|103 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|













