Directions: For the following questions answer them individually
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:Two trains cross each other in 14 seconds when running in opposite directions along parallel tracks. The faster train is 160 m long and crosses a lamp post in 12 seconds. If the speed of the other train is 6 km/hr less than the faster one, its length, in m, is
Explanation
Speed of the faster train = 160/12 = 40/3 m/s
Speed of the slower train = 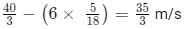
Sum of speeds (when the trains travel towards each other) = 40/3 + 35/3 = 25 m/s
Let the slower train be xx metres long; then: 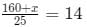
On solving, x = 190 m
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:If the area of a regular hexagon is equal to the area of an equilateral triangle of side 12 cm, then the length, in cm, of each side of the hexagon is
Explanation
Area of a regular hexagon = 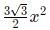
Area of an equilateral triangle = 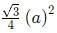 ; where a = side of the triangle.
; where a = side of the triangle.
Since the area of the two figures are equal, we can equate them as folllows:
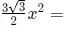
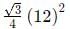
On simplifying: x2 = 24
∴ x = 2√6
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:Suppose the length of each side of a regular hexagon ABCDEF is 2 cm.It T is the mid point of CD,then the length of AT, in cm, is
Explanation
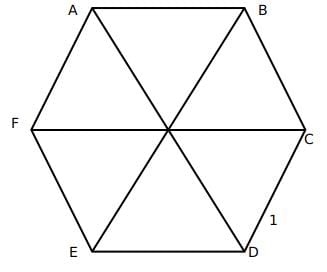
Since a regular hexagon can be considered to be made up of 6 equilateral triangles, a line joining the farthest vertices of a hexagon can be considered to be made up using the sides of two opposite equilateral triangle forming the hexagon. Hence, its length should be twice the side of the hexagon, in this case, 4 cm.
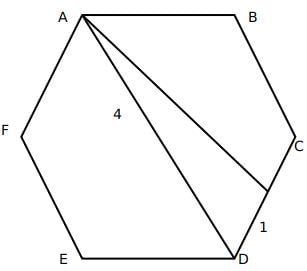
Now, AD divided the hexagon into two symmetrical halves. Hence, AD bisects angle D, and hence, angle ADC is 60∘
We can find out the value of AT using cosine formula:
AT2 = 42 + 12 - 2 x 1 x 4 Cos60
AT2 = 17 - 4 = 13
AT = √13
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:Anu, Vinu and Manu can complete a work alone in 15 days, 12 days and 20 days, respectively. Vinu works everyday. Anu works only on alternate days starting from the first day while Manu works only on alternate days starting from the second day. Then, the number of days needed to complete the work is
Explanation
Let the total amount of work be 60 units.
Then Anu, Vinu, and Manu do 4, 5, and 3 units of work per day respectively.
On the 1st day, Anu and Vinu work. Work done on the 1st day = 9 units
On the 2nd day, Manu and Vinu work. Work done on the 2nd day = 8 units
This cycle goes on. And in 6 days, the work completed is 9+8+9+8+9+8 = 51 units.
On the 7th day, again Anu and Vinu work and complete the remaining 9 units of work. Thus, the number of days taken is 7 days.
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:The amount Neeta and Geeta together earn in a day equals what Sita alone earns in 6 days. The amount Sita and Neeta together earn in a day equals what Geeta alone earns in 2 days. The ratio of the daily earnings of the one who earns the most to that of the one who earns the least is
Explanation
Let the amounts Neeta, Geeta, and Sita earn in a day be n, g, and s respectively.
Then, it has been given that:
n + g = 6s - i
s + n = 2g -ii
ii-i, we get: s - g = 2g - 6s
7s = 3g.
Let g be 7a. Then s earns 3a.
Then n earns 6s-g = 18a - 7a = 11a.
Thus, the ratio is 11a:3a = 11:3
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:Onion is sold for 5 consecutive months at the rate of Rs 10, 20, 25, 25, and 50 per kg, respectively. A family spends a fixed amount of money on onion for each of the first three months, and then spends half that amount on onion for each of the next two months. The average expense for onion, in rupees per kg, for the family over these 5 months is closest to
Explanation
Let us assume the family spends Rs. 100 each month for the first 3 months and then spends Rs. 50 in each of the next two months.
Then amount of onions bought = 10, 5, 4, 2, 1, for months 1-5 respectively.
Total amount bought = 22kg.
Total amount spent = 100 + 100 + 100 + 50 + 50 = 400.
Average expense = 400/22
= Rs.18.18 ≈ 18
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:The number of groups of three or more distinct numbers that can be chosen from 1, 2, 3, 4, 5, 6, 7 and 8 so that the groups always include 3 and 5, while 7 and 8 are never included together is
Explanation
The possible arrangements are of the form
35 _ Can be chosen in 6 ways.
35 _ _ We can choose 2 out of the remaining 6 in 6C2 = 15ways. We remove 1 case where 7 and 8 are together to get 14 ways.
35 _ _ _We can choose 3 out of the remaining 6 in 6C3 = 20ways. We remove 4 cases where 7 and 8 are together to get 16 ways.
35 _ _ _ _We can choose 4 out of the remaining 6 in 6C4 = 15ways. We remove 6 case where 7 and 8 are together to get 9 ways.
35 _ _ _ _ _ We choose 1 out of 7 and 8 and all the remaining others in 2 ways.
Thus, total number of cases = 6 + 14 + 16 + 9 + 2 = 47.
Alternatively,
The arrangement requires a selection of 3 or more numbers while including 3 and 5 and 7, 8 are never included together. We have cases including a selection of only 7, only 8 and neither 7 nor 8.
Considering the cases, only 7 is selected.
We can select a maximum of 7 digit numbers. We must select 3, 5, and 7.
Hence we must have ( 3, 5, 7) for the remaining 4 numbers we have
Each of the numbers can either be selected or not selected and we have 4 numbers :
Hence we have _ _ _ _ and 2 possibilities for each and hence a total of 2*2*2*2 = 16 possibilities.
SImilarly, including only 8, we have 16 more possibilities.
Cases including neither 7 nor 8.
We must have 3 and 5 in the group but there must be no 7 and 8 in the group.
Hence we have 3 5 _ _ _ _.
For the 4 blanks, we can have 2 possibilities for either placing a number or not among 1, 2, 4, 6.
= 16 possibilities
But we must remove the case where neither of the 4 numbers are placed because the number becomes a two-digit number.
Hence 16 - 1 = 15 cases.
Total = 16+15+16 = 47 possibilities
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:Amal purchases some pens at ₹ 8 each. To sell these, he hires an employee at a fixed wage. He sells 100 of these pens at ₹ 12 each. If the remaining pens are sold at ₹ 11 each, then he makes a net profit of ₹ 300, while he makes a net loss of ₹ 300 if the remaining pens are sold at ₹ 9 each. The wage of the employee, in INR, is
Explanation
Let the number of pens purchased be n. Then the cost price is 8n. The total expenses incurred would be 8n+W, where W refers to the wage.
Then SP in the first case = 12 × 100 + 11 × (n−100)
Given profit is 300 in this case: 1200 + 11n - 1100 - 8n - W =3 00 ⇒ 3n - W = 200
In second case: 1200 + 9n - 900 - 8n - W = -300 (Loss). ⇒ W-n = 600.
Adding the two equations: 2n = 800
n = 400.
Thus W = 600 + 400 = 1000
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:A basket of 2 apples, 4 oranges and 6 mangoes costs the same as a basket of 1 apple, 4 oranges and 8 mangoes, or a basket of 8 oranges and 7 mangoes. Then the number of mangoes in a basket of mangoes that has the same cost as the other baskets is
Explanation
Let the cost of an apple, an orange and a mango be a, o, and m respectively.
Then it is given that:
2a + 4o + 6m = a + 4o + 8m
or a = 2m.
Also, a + 4o + 8m = 8o + 7m
10m - 7m = 4o
3m = 4o.
We can now express the cost of a basket in terms of mangoes only:
2a + 4o + 6m = 4m + 3m + 6m = 13m.
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:The number of integers n that satisfy the inequalities 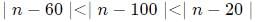 is
is
Explanation
We have
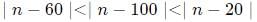
Now, the difference inside the modulus signified the distance of n from 60, 100, and 20 on the number line. This means that when the absolute difference from a number is larger, n would be further away from that number.
Example: The absolute difference of n and 60 is less than that of the absolute difference between n and 20. Hence, n cannot be ≤ 40, as then it would be closer to 20 than 60, and closer on the number line would indicate lesser value of absolute difference. Thus we have the condition that n>40.
The absolute difference of n and 100 is less than that of the absolute difference between n and 20. Hence, n cannot be ≤ 60, as then it would be closer to 20 than 100. Thus we have the condition that n>60.
The absolute difference of n and 60 is less than that of the absolute difference between n and 100. Hence, n cannot be ≥ 80, as then it would be closer to 100 than 60. Thus we have the condition that n<80.
The number which satisfies the conditions are 61, 62, 63, 64......79. Thus, a total of 19 numbers.
Alternatively
as per the given condition : 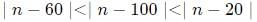
Dividing the range of n into 4 segments. (n < 20, 20<n<60, 60<n<100, n > 100 )
1) For n < 20.
|n-20| = 20-n, |n-60| = 60- n, |n-100| = 100-n
considering the inequality part :\left|n-100\right|<\ \left|n\ -20\right|∣n−100∣< ∣n −20∣
100 -n < 20 -n,
No value of n satisfies this condition.
2) For 20 < n < 60.
|n-20| = n-20, |n-60| = 60- n, |n-100| = 100-n.
60- n < 100 - n and 100 - n < n - 20
For 100 -n < n - 20.
120 < 2n and n > 60. But for the considered range n is less than 60.
3) For 60 < n < 100
|n-20| = n-20, |n-60| = n-60, |n-100| = 100-n
n-60 < 100-n and 100-n < n-20.
For the first part 2n < 160 and for the second part 120 < 2n.
n takes values from 61 ................79.
A total of 19 values
4) For n > 100
|n-20| = n-20, |n-60| = n-60, |n-100| = n-100
n-60 < n - 100.
No value of n in the given range satisfies the given inequality.
Hence a total of 19 values satisfy the inequality.
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:How many three-digit numbers are greater than 100 and increase by 198 when the three digits are arranged in the reverse order?
Explanation
Let the numbers be of the form 100a+10b+c, where a, b, and c represent single digits.
Then (100c + 10b + a) - (100a + 10b + c) = 198
99c - 99a = 198
c - a = 2.
Now, a can take the values 1-7. a cannot be zero as the initial number has 3 digits and cannot be 8 or 9 as then c would not be a single-digit number.
Thus, there can be 7 cases.
B can take the value of any digit from 0-9, as it does not affect the answer. Hence, the total cases will be 7× 10=70.
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:Anil invests some money at a fixed rate of interest, compounded annually. If the interests accrued during the second and third year are ₹ 806.25 and ₹ 866.72, respectively, the interest accrued, in INR, during the fourth year is nearest to
Explanation
Let the principal amount be P and the interest rate be r.
Then 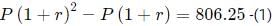
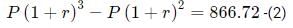
Dividing (2) by (1), we get:
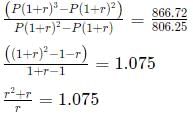
r = 0.075 or 7.5%
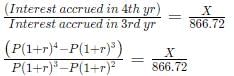
Dividing numerator and denominator by P(1 + r)2
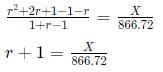
X = 1.075 × 866.72 = 931.72
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:Suppose hospital A admitted 21 less Covid infected patients than hospital B, and all eventually recovered. The sum of recovery days for patients in hospitals A and B were 200 and 152, respectively. If the average recovery days for patients admitted in hospital A was 3 more than the average in hospital B then the number admitted in hospital A was
Explanation
Let the number of Covid patients in Hospitals A and B be x and x+21 respectively. Then, it has been given that:
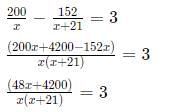
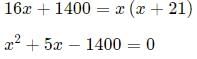
(x + 40)(x - 35) = 0
Hence, x = 35.
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:A circle of diameter 8 inches is inscribed in a triangle ABC where ∠ABC=90∘. If BC = 10 inches then the area of the triangle in square inches is
Explanation
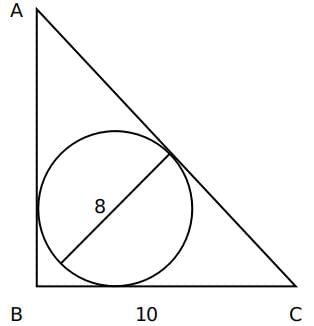
We know that Inradius = 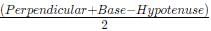
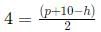
h - p = 2 or h = p + 2.
Now, p2 + 100 = h2
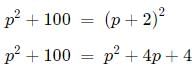
4p = 96
p = 24.
Hence, Area = 1/2 x 10 x 24 = 120
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself: is negative if and only if
is negative if and only if
Explanation
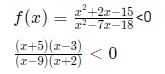
We have four inflection points -5, -2, 3, and 9.
For x < -5, all four terms (x + 5), (x - 3), (x - 9), (x + 2) will be negative. Hence, the overall expression will be positive. Similarly, when x > 9, all four terms will be positive.
When x belongs to (-2,3), two terms are negative and two are positive. Hence, the overall expression is positive again.
We are left with the range (-5,-2) and (3,9) where the expression will be negative.
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:If 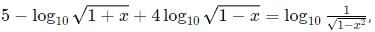 then 100x equals
then 100x equals
Explanation
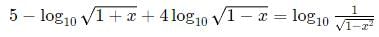
We can re-write the equation as:
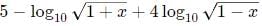 =
= 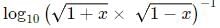
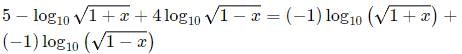
5 = 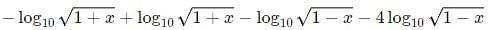
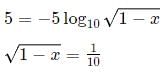
Squaring both sides: 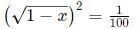
Therefore,
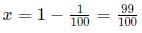
Hence, 100x = 100 x 99/100 = 99
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:Amar, Akbar and Anthony are working on a project. Working together Amar and Akbar can complete the project in 1 year, Akbar and Anthony can complete in 16 months, Anthony and Amar can complete in 2 years. If the person who is neither the fastest nor the slowest works alone, the time in months he will take to complete the project is
Explanation
Let the total work be 48 units. Let Amar do 'm' work, Akbar do 'k' work, and Anthony do 'n' units of work in a month.
Amar and Akbar complete the project in 12 months. Hence, in a month they do 48/12 = 4 units of work
m + k = 4.
Similarly, k + n = 3, and m + n = 2.
Solving the three equations, we get m = 3/2, k = 5/2, n = 1/2
Here, Amar works neither the fastest not the slowest, and he does 1.5 units of work in a month. Hence, to complete the work, he would take 48/1.5 = 32 months
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:If x0 = 1, x1 = 2 and xn+2 = 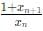 , n = 0,1,2,3,......, then x2021 is equal to
, n = 0,1,2,3,......, then x2021 is equal to
Explanation
x0 = 1
x1 = 2
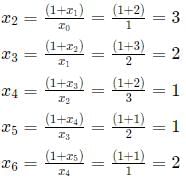
Hence, the series begins to repeat itself after every 5 terms. Terms whose number is of the form 5n are 1, 5n + 1 are 2... and so on, where n = 0,1,2,3,....
2021 is of the form 5n + 1. Hence, its value will be 2.
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:The strength of an indigo solution in percentage is equal to the amount of indigo in grams per 100 cc of water. Two 800 cc bottles are filled with indigo solutions of strengths 33% and 17%, respectively. A part of the solution from the first bottle is thrown away and replaced by an equal volume of the solution from the second bottle. If the strength of the indigo solution in the first bottle has now changed to 21% then the volume, in cc, of the solution left in the second bottle is
Explanation
Let Bottle A have an indigo solution of strength 33% while Bottle B have an indigo solution of strength 17%.
The ratio in which we mix these two solutions to obtain a resultant solution of strength 21%
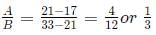
Hence, three parts of the solution from Bottle B is mixed with one part of the solution from Bottle A. For this process to happen, we need to displace 600 cc of solution from Bottle A and replace it with 600 cc of solution from Bottle B {since both bottles have 800 cc, three parts of this volume = 600cc}.As a result, 200 cc of the solution remains in Bottle B.
Hence, the correct answer is 200 cc.
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:Identical chocolate pieces are sold in boxes of two sizes, small and large. The large box is sold for twice the price of the small box. If the selling price per gram of chocolate in the large box is 12% less than that in the small box, then the percentage by which the weight of chocolate in the large box exceeds that in the small box is nearest to
Explanation
Let the selling price of the Large and Small boxes of chocolates be Rs.200 and Rs.100 respectively. Let us consider that the Large box has L grams of chocolate while the Small box has S grams of chocolate.
The relation between the selling price per gram of chocolate can be represented as:
200/L = 0.88 x 100/S
On solving we obtain the ratio of the amount of chocolate in each box as: L/S = 25/11
The percentage by which the weight of chocolate in the large box exceeds that in the small box = (25/11 - 1) x 100 ≈ 127%
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:The natural numbers are divided into groups as (1), (2, 3, 4), (5, 6, 7, 8, 9), ….. and so on. Then, the sum of the numbers in the 15th group is equal to
Explanation
The first number in each group: 1, 2, 5, 10, 17.....
Their common difference is in Arithmetic Progression. Hence, the general term of the series can be expressed as a quadratic equation.
Let the quadratic equation of the general term be ax2 + bx + c
1st term = a + b + c = 1
2nd term = 4a + 2b + c = 2
3rd term = 9a + 3b + c = 5
Solving the equations, we get a = 1, b = -2, c = 2.
Hence, the first term in the 15th group will be (15)2 - 2(15) + 2 = 197
We can see that the number of terms in each group is 1, 3, 5, 7.... and so on. These are of the form 2n - 1. Hence, the number of terms in 15th group will be 29. Hence, the last term in the 15th group will be 197 + 29 - 1 = 225.
Sum of terms in group 15 = 29/2(197 + 225) = 6119
Alternatively,
The final term in each group is the square of the group number.
In the first group 1, second group 4, ............
The final element of the 14th group is (14)2 = 196, similarly for the 15th group this is : (15)2 = 225
Each group contains all the consecutive elements in this range.
Hence the 15th group the elements are:
(197, 198, ................................225).
This is an Arithmetic Progression with a common difference of 1 and the number of element 29.
Hence the sum is given by
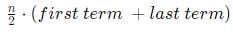
= 29/2 . (197 + 225)
= 6119
Report a problem
Question for Quant For CAT 2021 (Slot - 1)
Try yourself:If r is a constant such that | x2 − 4x − 13| = r has exactly three distinct real roots, then the value of r is
Explanation
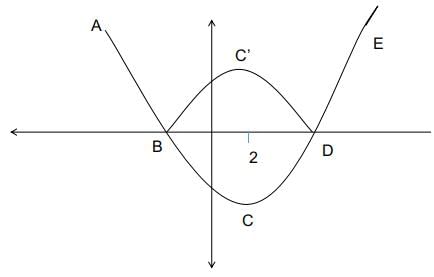
The quadratic equation of the form | x2 − 4x − 13| = r has its minimum value at x = -b/2a, and hence does not vary irrespective of the value of x.
Hence at x = 2 the quadratic equation has its minimum.
Considering the quadratic part : | x2 − 4x − 13| as per the given condition, this must-have 3 real roots.
The curve ABCDE represents the function | x2 − 4x − 13|. Because of the modulus function, the representation of the quadratic equation becomes :
ABC'DE.
There must exist a value, r such that there must exactly be 3 roots for the function. If r = 0 there will only be 2 roots, similarly for other values there will either be 2 or 4 roots unless at the point C'.
The point C' is a reflection of C about the x-axis. r is the y coordinate of the point C' :
The point C which is the value of the function at x = 2, = 22 − 8 − 13
= -17, the reflection about the x-axis is 17.
Report a problem
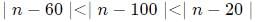 is
is
 is negative if and only if
is negative if and only if
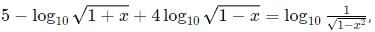 then 100x equals
then 100x equals
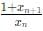 , n = 0,1,2,3,......, then x2021 is equal to
, n = 0,1,2,3,......, then x2021 is equal to
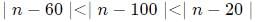 is
is
 is negative if and only if
is negative if and only if
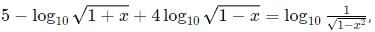 then 100x equals
then 100x equals
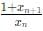 , n = 0,1,2,3,......, then x2021 is equal to
, n = 0,1,2,3,......, then x2021 is equal to