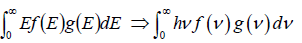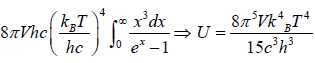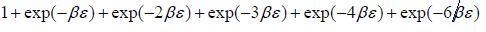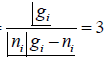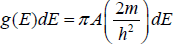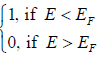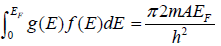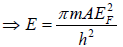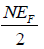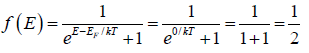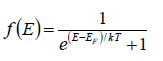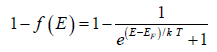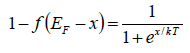Quantum Mechanical Identical Particle | Kinetic Theory & Thermodynamics - Physics PDF Download
Bose Einstein distribution
In quantum statistics, Bose–Einstein statistics (or more colloquially B–E statistics) is one of two possible ways in which a collection of indistinguishable particles may occupy a set of available discrete energy state . The aggregation of particles in the same state, which is a characteristic of particles obeying Bose–Einstein statistics .who recognized that a collection of identical and indistinguishable particles can be distributed in this way.
The Bose–Einstein statistics apply only to those particles not limited to single occupancy of the same state—that is, particles that do not obey the Pauli exclusion restrictions.
Such particles have integer values of spin and are named boson , after the statistics that
correctly describe their behavior.
The wave function of particle will overlap to each other because mean separation of particles is less than the thermal wavelength, which is identified by λ.
(where 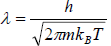 is defined as the thermal wavelength )
is defined as the thermal wavelength )
Suppose there are l states with energies, E1,E2,E3,...El and degeneracy g1,g2,g3...gl. Respectively, in which the particles are distributed. If there is N numbers of indistinguishable boson particles out of these n1,n2,n3.....nl particles is adjusted in energy level E1,E2,E3,...El respectively.
It is given 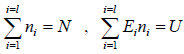
The total no. of arrangements of the particles in the given distributions is given by
W = 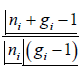 , W =
, W = 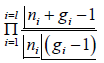
If ni and gi are large numbers, we can omit 1 in comparison to them,
So we have, W = 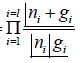
The Bose Einstein distribution of the particle among various states ni = 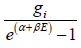
The Bose-Einstein energy distribution is,f(E) = 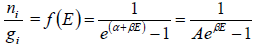
Where, β = 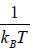 and
and 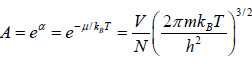
Here, μ is chemical potential which is generally a function of T . when A >> 1, Bose- Einstein gas reduces to the Maxwell-Boltzmann gas. The chemical potential for Bose gas
is negative, but for photon gas is zero.
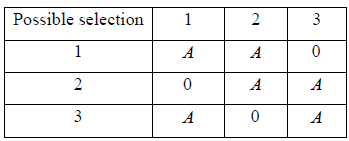
Example 11: Two indistinguishable boson particles have to be adjusted in a state whose degeneracy is three.
(a) How many ways the particles can be adjusted?
(b) Show all arrangement.
(a) ni = 2, gi = 3, Wi =
= 6 ways
(b) Total number of arrangement for 2 indistinguishable boson particles in state whose degeneracy is 3.
Examples 12: (a) Write down distribution function of photon at temperature T , if average energy in each state is given by ε= hv.
(b) What is density of state of photon gas between frequency v to v + dv
(c) Write down expression of no of particle for photon gas at temperature T .
(d) Write down expression of average energy for photon gas at temperature T.
(a) The Bose Einstein distribution is given by f(E) =
where
For boson μ = 0 so
For if average energy in each state is given by ε= hv then f(E) =
.
(b) If j is quantum number associate with frequency v then total no of frequency between v to v + dv is same as the number of points between j to j + dj . The volume of spherical shell of radius j and thickness dj is 4πj2dj
Hence all three component of j is positive (same as particle in box) and there are two direction of polarization so degeneracy g = 2 .
So number of standing wave g(j)dj =
It is given,
So density of standing wave in cavity is given by g(v)dv =
(c) N =
N =
put
The integral have value, N =
(d) U =
U =
U =
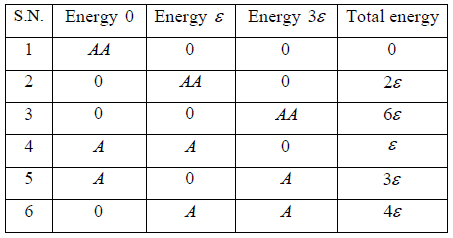
Example 13: A system consisting of two boson particles each of which can be any one of three quantum state of respective energies o, ,3 is in equilibrium at temperature T. write the expression of partition function.
Two boson can be distributed in three given state with their respective energy level shown in table
Z =
Fermi Dirac Distribution
In quantum statistics, Fermi–Dirac statistics describes distribution of particles in a system comprising many identical particles that obey the Pauli Exclusion Principle (The Pauli Exclusion Principle is the quantum mechanical principle that no two identical fermions (particles with half-integer spin) may occupy the same quantum state simultaneously.)
Fermi–Dirac (F–D) statistics applies to identical particles with half odd integer spin in a system in thermal equilibrium. Additionally, the particles in this system are assumed to have negligible mutual interaction. This allows the many-particle system to be described
in terms of single-particle energy states. The result is the F-D distribution of particles over these states and includes the condition that no two particles can occupy the same state, which has a considerable effect on the properties of the system. Since F-D statistics applies to particles with half-integer spin, these particles have come to be called fermions. It is most commonly applied to electrons, which are fermions with spin 1/2.
No. of ways W in which ni indistinguishable particles to place in level with the
condition that only one particle or no particle can be placed in gi each level i.e. identical
particles that obey the Pauli exclusion principle. (It is given 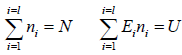 )
)
It is given by, W = 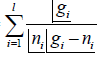
Fermi-Dirac distribution of the particles among various states is given by
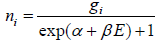
So Fermi Dirac distribution f(E) = 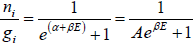
where β = 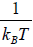 and A =
and A = 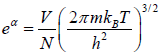
when A >>1, Fermi-Dirac gas reduces to the Maxwell-Boltzmann gas. Fermi-Dirac gas is said to be weakly degenerate when A > 1 , degenerate when A<1 and strongly degenerate when A = 0 . Strongly degenerate Fermi gas A < 1
The Fermi-Dirac energy distribution is, f(E)= 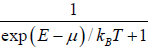
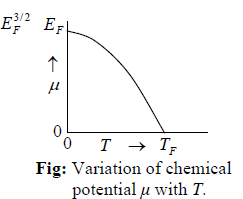
Where, μ is the chemical potential which is a function of T , i.e., μ = μ (T ) . The gas is
strongly degenerate (A= 0) at T = 0 , where μ = μ(0) = EF . The limiting chemical potential is known as the Fermi energy EF of the gas and the distribution function can be
written as 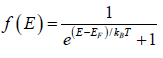
Strongly degenerate Fermi gas at T = 0
At T = 0 , when E<EF we have f(E) = 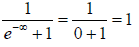
At T = 0 , when E>EF we have f(E) =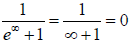

Fermi function f (E) versus E at T
The number of energy states in the energy range from E to E + dE is 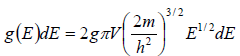 . Here, g is the spin degeneracy, g = (2s +1) , where s is the spin quantum number of a particle.
. Here, g is the spin degeneracy, g = (2s +1) , where s is the spin quantum number of a particle.
The number of particles in the energy range from E to E + dE at T = 0 is
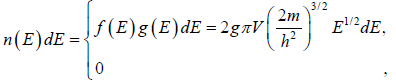 for E<EF
for E<EF
N = 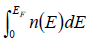 =
= 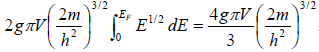
Thus, the Fermi energy is 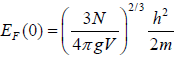
and the Fermi temperature TF is defined as TF = 
The Fermi momentum pF is given by pF = 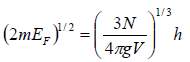
Total energy of the gas at T = 0 is
U = 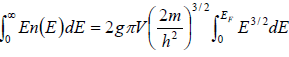 =
= 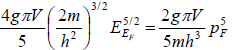
Thus, at T = 0 we have U/N = 3/5EF
Example 14: What is no. of ways if two fermions have to adjust in energy state whose degeneracy is three.
gi = 3, ni = 2 , W =
Two indistinguishable particles is shown by A, A
Example 15: Fermions of mass m are kept in two dimensional box of area A at temperature T = 0
(a) What is total number of particle if is Fermi energy EF.
(b) What is the energy of the system if is Fermi energy EF.
(c) Write expression of energy in term of EF and N
For two dimensional systems, density of state
And distribution function at temperature T = 0 , is given by
(a) N =
(b) E =
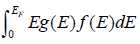
,
(c) E =
Example 16: (a) If Fermi gas is at temperature T > 0 what will f(EF) .
(b) At E = EF + x , find the fraction of occupied levels.
(c) At E = EF - x , find fraction of unoccupied levels.
(a) It is also interesting to note that at T = 0 , when E = EF we have
(b) At T > 0, fraction of levels above EF are occupied and a fraction of levels below EF are vacant. The fraction of occupied levels at the energy E is
At E = EF + x , find the fraction of occupied levels is
(c) The fraction of unoccupied levels at the energy E is
At E = EF - x , find the fraction of occupied levels is
|
6 videos|20 docs|32 tests
|
FAQs on Quantum Mechanical Identical Particle - Kinetic Theory & Thermodynamics - Physics
| 1. What is the Fermi-Dirac distribution in quantum mechanics? |  |
| 2. How does the Fermi-Dirac distribution differ from the classical Boltzmann distribution? |  |
| 3. What are the key features of the Fermi-Dirac distribution function? |  |
| 4. How does the Fermi-Dirac distribution relate to the behavior of electrons in a material? |  |
| 5. How is the Fermi-Dirac distribution used in practical applications? |  |